巧用数形结合，培养学生的形象思维

胡双燕

数形结合既是一种重要的数学思想，又是一种常用的数学方法。在小学阶段的数学学习中，数形结合的思想有着非常重要的优势。形象思维是指以具体的数学形象或者表象为思维内容，以此来揭示数学对象的本质或规律的思维活动。小学生的思维仍然以具体的形象思维为主要形式，慢慢地向抽象逻辑思维过渡。在这个过渡的过程中，形象思维起着至关重要的作用，对学生以后的数学学习有着重要的影响。所以，在教学中，我们可以借助数形结合思想中的直观图形手段，使之形象化、直观化，丰富其表象，引导学生进行想象，进一步培养学生的形象思维能力。

一、充分利用直观教具，丰富学生的表象

表象是存储在头脑中的直觉印象的再现，是形象思维的基础，学生的表象感知越丰富，形象思维就越强。在小学数学学习中，抽象的数学概念和复杂的数量关系对小学生来说，理解起来一般比较困难。如果教师能用图片、模具、教具等手段组织教学，使抽象的概念具体化、形象化，就能让学生经历从感知表象到认识实质的思维过程，帮助学生理解和记忆，从而培养学生的形象思维能力。

【案例1】人教版三年级“数学广角”中的“搭配”一课。

教师出示：

问：一共有多少种不同的搭配方法？

小组分工合作，通过摆学具的方式，把找到的搭配方法用文字、图形、数字等方式记录下来。

汇报环节：

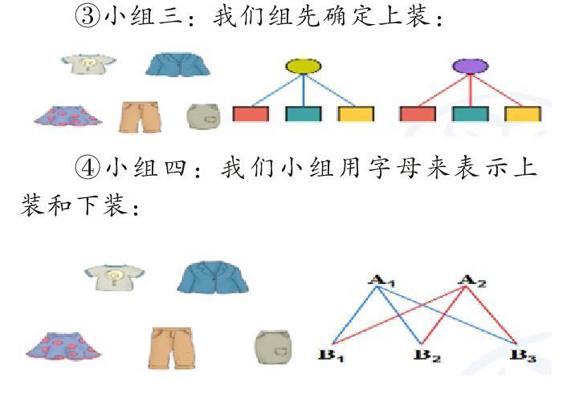
①小组一：我们是用画一画的方法，把每一种可以进行搭配的衣服画下来。

②小組二：我们用连一连的方法，在每一种搭配方法上连一条线。

③小组三：我们组先确定上装：

④小组四：我们小组用字母来表示上装和下装：

师：刚才同学们都用自己喜欢的方式记录了不同的搭配方法，这几种方法中，你觉得哪种形式比较简单好记呢？

生：我觉得用符号记录比较简单。

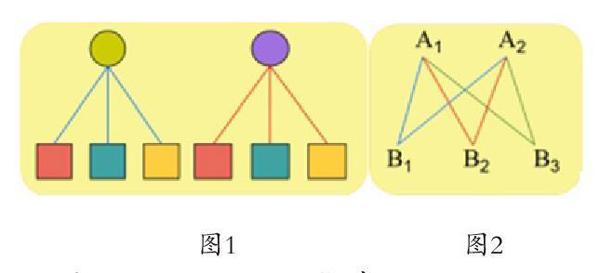
师：请同学们仔细观察图1和图2，想想能不能用算式把摆的情况表示出来？

生1：可以用“3+3”表示。

生2：可以用“3×2”或“2×3”来表示。

在以上的教学中，因为有了“搭配图”这个桥梁，教师便可不失时机地为学生提供恰当的形象材料，将抽象的组合规律具体化，让学生明白了不同搭配方法的个数与上衣和下装的件数有关，使解题思路具象化了。以“形”助“数”，实现了抽象数学知识的直观体现，不仅让学生掌握了简单的搭配规律，而且让学生在感知基础上丰富了数学表象思维，为其数学形象思维的发展奠定了基础。

二、数形结合创设情境，引导学生进行想象

想象是形象思维的一种高级方式，它的实质是表象的改造过程。小学生有其独特的思维特点，因此，培养小学生的形象思维，应该根据其特点，以具体、直观的教学为主。但是，如果想让学生的形象思维得到更大的发展和提高，教学中教师必须数形结合，巧妙创设情境，引导学生进行想象，提升形象思维的能力。

【案例2】五年级下册“图形的旋转”：教师在让学生理解了旋转的三个要素即旋转中心、旋转方向以及旋转角度后，接下来可以这样开展教学：

（1）让学生合作学习讨论：

师：课件出示图形：，时针从12点到1点是怎样旋转的？你能用旋转的三个要素说说吗？

生1：我认为从12到1，指针绕o点顺时针旋转了30°。

（2）加深认识：看动画说说时针的旋

转（如图）。

你能按照刚刚的说法描述一下这个指针的运动吗？

生2：从12到2，时针绕o点顺时针旋转了60°。

师：声音很响亮，回答得很准确。

（3）师：同学们对旋转的三个要素掌握得很不错。现在请同学们闭上眼睛，想象一下，指针从3到6、从12到6分别又是怎样运动的？

生3：从3到6，时针绕o点顺时针旋转90°。

生4：从12到6，时针绕o点逆时针旋转180°。

师：我们来看一下他们说得对不对（课件演示验证）。

在以上的案例中，教师用数形结合方法创设情境，有层次地设计教学;在学生认识了旋转的三个要素后，引导学生进行想象，让学生在头脑中进一步感知旋转的整个过程，指导学生将复杂的问题简单化、抽象的问题形象化，既增强了学生对旋转知识的了解和掌握，又培养了学生的数学想象能力，从而促进了学生形象思维的发展，有效地提高了学生分析问题、解决问题的能力，为学生终身的发展奠定了坚实的基础。

参考文献：

[1]单俊.数形结合求解小学数学应用题的典型应用[J].中国多媒体与网络教学学报（电子版），2018（1）.

[2]占红梅.核心素养视域下小学生数感的培养[J].基础教育研究，2018（16）.

[3]潘文芳.数形结合，提升素养——例谈数形结合思想方法的渗透[J].数理化解题研究：高中版，2016（17）.