考虑页岩弱层理的水力裂缝扩展路径三维数值模拟

周文高，王素兵，杨焕强

1中国石油川庆钻探工程有限公司井下作业公司2长江大学石油工程学院

0 引言

我国页岩气资源储量丰富，有效勘探面积达43×104km2，可采资源量介于11.5×1012～36.1×1012m3，居世界前列［1］。弱层理界面是页岩储层的典型特征，决定了体积压裂复杂缝网的形成。

国内外学者针对水力裂缝在弱界面处的扩展问题，进行了大量研究。周健等［2］、陈勉等［3］利用室内实验揭示了多裂缝扩展机理，陈治喜等［4］、赵海峰等［5］、Liu等［6］分别提出了垂直裂缝在层状储层界面扩展路径选择的判断准则。这些实验与解析方法虽然能够在一定程度上描述垂直裂缝在层状地层的扩展形式与规律，但以上研究并未考虑层状岩石的界面特性对裂缝扩展路径的影响。Chen等［7］利用Cohesive单元描述了层状界面特征，潘睿等［8］、孙博等［9］分别利用Cohesive单元建立了水力裂缝穿层扩展数值模型，得到了裂缝穿层扩展规律。然而，以上基于交叉Cohesive单元的水力裂缝在层间界面扩展的数值模型均为二维模型，只能探索缝高的变化规律。

基于此，本文利用交叉Cohesive单元，建立页岩体积压裂过程中水力裂缝在弱层理面扩展的三维数值模型，研究不同地应力差、层理界面特性、注液速率等条件下的水力裂缝穿层规律。

1 威远页岩力学特性参数

井区内A井的储层最小水平主应力为58～72 MPa，最大水平主应力为63～96 MPa。

为得到页岩层理界面力学参数，参考Xiong等［10］、J.L.Kavanagh等［11］、吕有厂等［12］、赵子江等［13］研究成果，采用三点弯曲加载实验与数字图像法测试了川庆威远地区露头页岩岩心的层理界面拉伸刚度。岩心试件采用线切割加工成12个长×宽×高为200 mm×40 mm×40 mm的长方体试件，预制裂缝开口高度为8 mm，预制裂缝高度与岩心高度之比为0.2。

结合数字图像系统与三点弯曲加载系统，设置0.02 mm/min的加载速度，采集并计算任意时刻试件表面位移变化，依此计算界面拉伸刚度，如式（1）所示［10］。

式中：dσ—拉伸应力变化量；

d u—拉伸位移变化量。

拉应力σ计算如下：

式中：S—试件跨度，m；

p—试验机荷载，N；

B—试件宽度，m；

W—试件高度，m；

a0—预制裂纹高度，m。

以1号试件为例绘制实验过程中的拉伸应力—位移曲线，其加载过程中拉应力与张开位移变化曲线如图1所示。

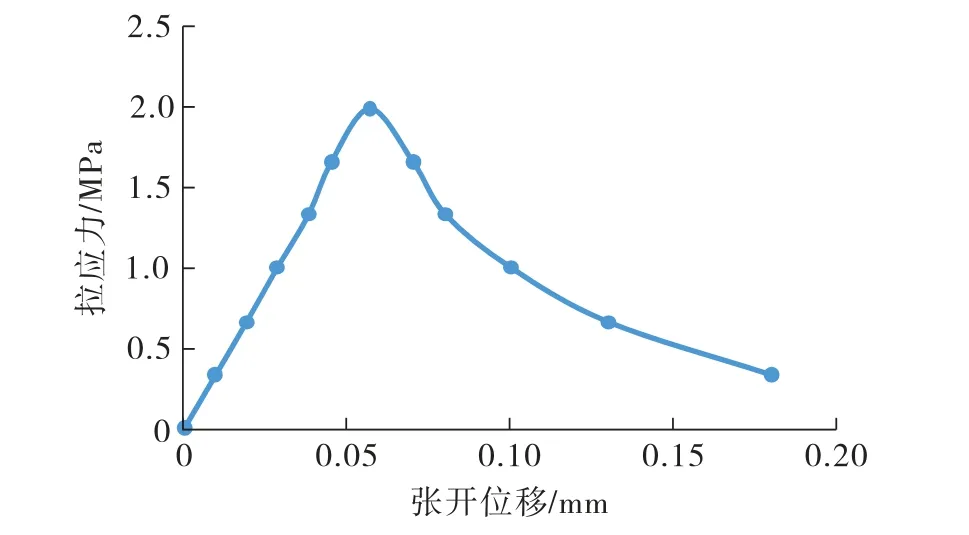
图1 试件1拉应力—张开位移曲线

利用公式（1）计算各实验试件的界面刚度，结果如表1所示。

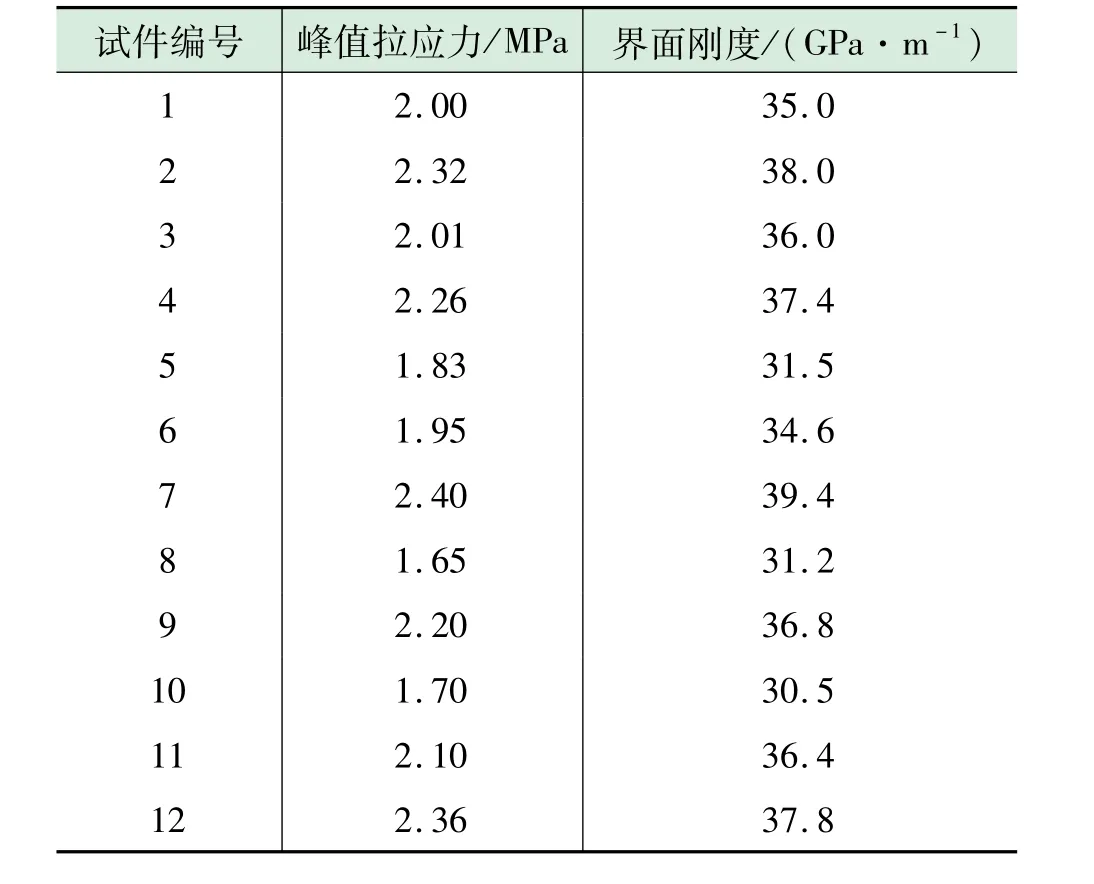
表1 实验测试结果

2 粘聚力模型模拟页岩层理

采用Cohesive模型描述页岩层理界面，其本构关系数学表达式为［14］：

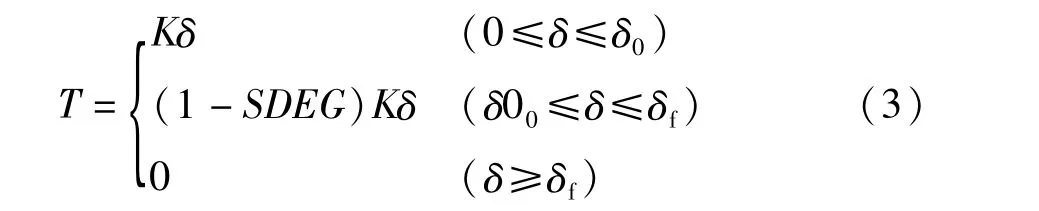
Cohesive模型破坏准则将界面破坏分为三个过程：

（1）牵引位移0＜δ＜δ0，此阶段层理属于线弹性阶段，此时损伤因子SDEG＝0，当拉伸位移δ＝δ0时牵引力最大，损伤开始。

（2）牵引位移δ0＜δ＜δf，界面损伤阶段，损伤因子0＜SDEG＜1，拉伸位移δ＝δf时界面完全损伤，界面脱离。

（3）牵引位移δ＞δf，界面完全破坏，SDEG＝1。曲线与横坐标轴围成的三角形面积为界面破坏过程的断裂能［15］。

3 三维有限元模型

3.1 几何及网格模型的建立

建立如图2所示裂缝长、宽、高方向分别为500 m×50 m×70 m的1/2三维几何模型。考虑上下两个平行的页岩弱胶结层理界面，注液点位于两个平行弱胶结层理界面中间位置，其中上下层厚度为25 m，中间层厚度为20 m。网格划分采用单精度加密网格，在水力裂缝长度、宽度、高度方向上均由远端向注液点方向加密，共划分网格283 103个。

图2 1/2三维几何模型

采用带有孔隙压力自由度的COH3D8P粘聚力单元模拟页岩层理面，带有孔隙压力自由度的C3D8P单元模拟页岩本体，模型参数设置见表2。

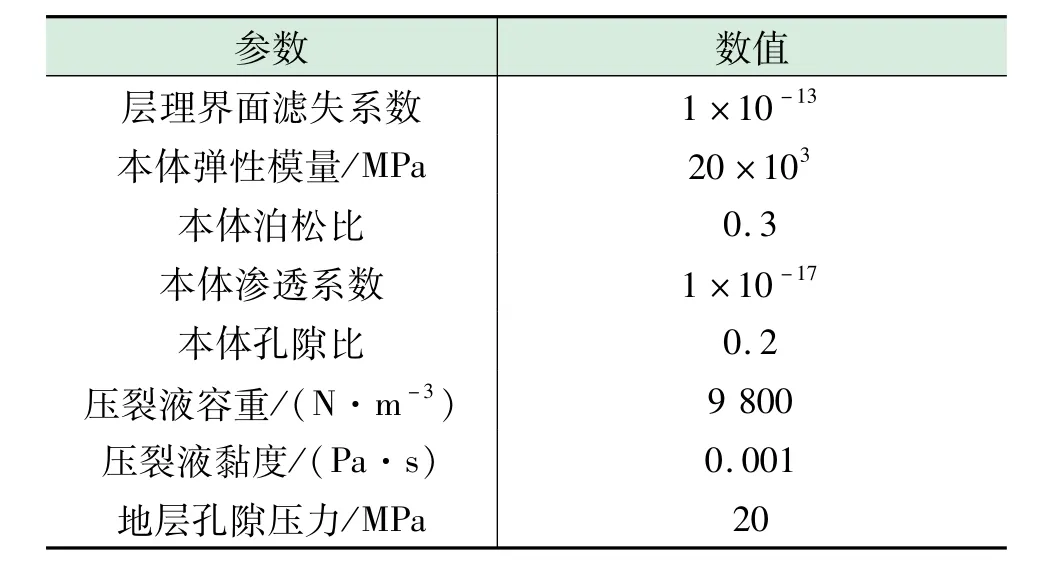
表2 模型参数设置

3.2 交叉Cohesive单元设置

采用零厚度Cohesive孔隙压力单元模拟页岩弱胶结层理面及水力裂缝扩展过程中的人工裂缝，通过作用在裂缝面上的压裂液控制Cohesive单元的破坏过程，同时耦合相邻岩石单元的变形过程，相交Cohesive处理方式如图3所示［9］。

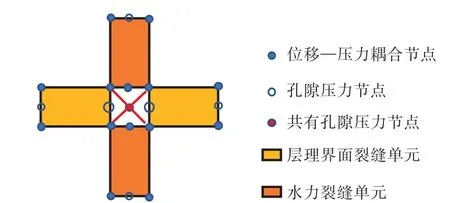
图3 天然裂缝与水力裂缝交汇点处理方式

利用ABAQUS软件网格模块中的Merge工具将层理界面与裂缝扩展路径的两个Cohesive单元中间节点合并为一个共有的孔隙压力节点来传递压裂液产生的缝内压力，中间节点合并后的结果见图4。

图4 相交Cohesive单元中间节点合并结果

4 数值模拟计算结果

4.1 地应力差影响

不同地应力差条件下水力裂缝沿层理界面的扩展路径如表3所示。其中页岩层理面临界能量释放率为70 N/m、临界最大拉应力为2 MPa；页岩本体临界能量释放率为150 N/m、抗拉强度为6 MPa；注液速率12 m3/s。数值模拟过程中保证这些参数不变，改变地应力变化，计算得到水力裂缝界面处的扩展路径。编号采用地应力差加最小水平地应力的方式，例如0-60表示地应力差为0，最小水平地应力为60 MPa。

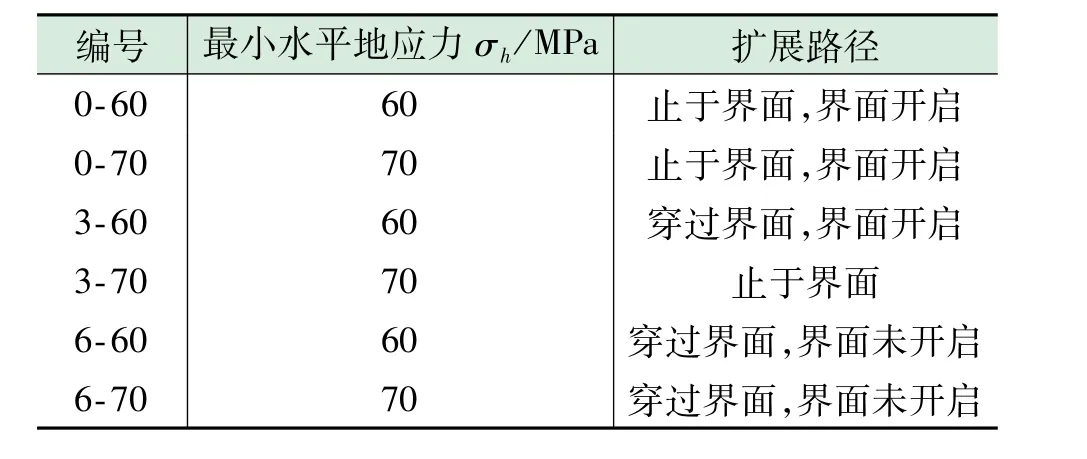
表3 不同地应力条件下水力裂缝界面处扩展路径

从表3中垂直裂缝穿层扩展路径结果可以看出，不同地应力差对裂缝扩展路径有着显著影响。地应力差为0时，垂直裂缝均未穿过层理界面，开启了层理界面；地应力差为3 MPa时，页岩层理界面都未开启，当最小水平地应力较小为60 MPa时，垂直裂缝穿过界面，当最小水平地应力较大为70 MPa时，垂直裂缝在界面处停止扩展；地应力差为6 MPa时，垂直裂缝均穿过界面，界面也并未开启。

可以看出，较大的地应力差有助于垂直裂缝穿层形成穿层裂缝，而较小的地应力差将会增大层理界面开启的可能；其次，对于地应力差相同的情况，最小水平地应力影响垂直裂缝扩展路径，最小水平地应力越小，裂缝约容易穿透层理界面。

图5与图6分别表示裂缝扩展过程中裂缝半缝长与裂缝高度的变化曲线。从图5可以看出，当地应力差相同时，最小水平地应力越大，缝长越大，例如图5中0-70、3-70、6-70分别比0-60、3-60、6-60的缝长大。对于地应力差为3 MPa的情况，当最小水平地应力为70 MPa时，出现了水力裂缝止于界面的情况，在图5中可以看出，此种情况下缝长最长，可见水力裂缝在高度方向的停止扩展也将促使水力裂缝长度的增长。

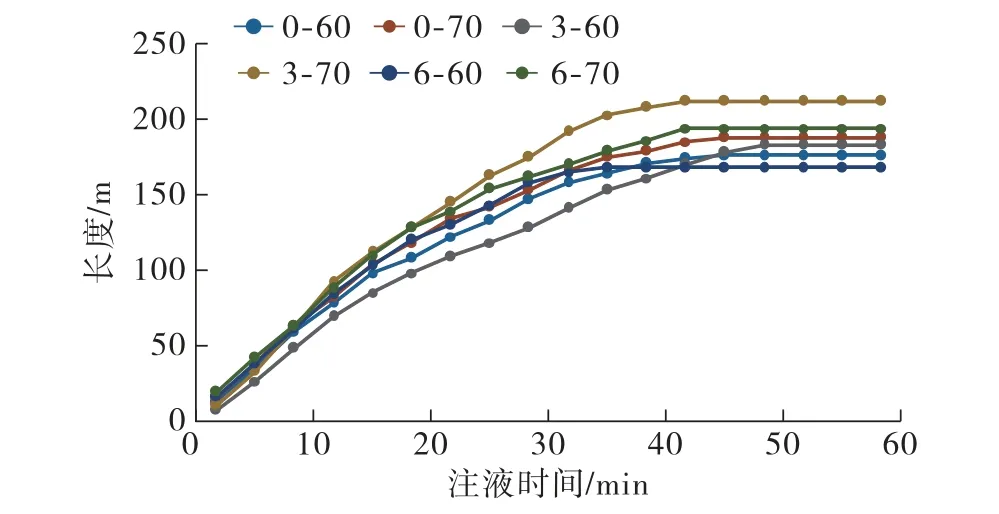
图5 半缝长随时间变化曲线

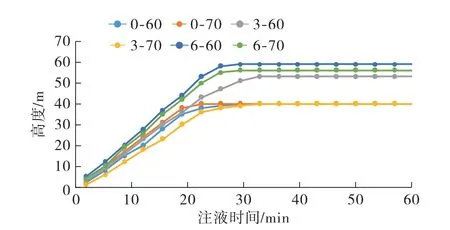
图6 缝高随时间变化曲线

由图6可知，20 min前后，曲线0-60、0-70、3-70的垂直裂缝高度曲线出现了偏转，偏转后的曲线高度为40 m，这是因为垂直裂缝高度顶端到达了层理界面处，造成层理界面的开启，从而造成水力裂缝高度增长受到影响。

4.2 层理面强度影响

表4为不同层理面刚度条件下水力裂缝的界面处扩展路径。其中页岩层里面能量释放率为70 N/m、最大拉应力为2 MPa；本体Cohesive拉伸刚度值为40 GPa/m、能量释放率为150 N/m、最大拉应力为6 MPa；注液速率12 m3/s。数值模拟过程中保证这些参数不变，改变层理面刚度值，计算得到水力裂缝界面处的扩展路径。

由表4计算结果可知，界面刚度值为2 GPa/m时，水力裂缝止于层理界面且引起界面的滑移，形成“T”型缝；当界面刚度值为20 GPa/m时，水力裂缝穿过界面且引起界面的滑移，形成“十”型缝；当界面刚度值为35 GPa/m时，水力裂缝穿过界面，界面未开启。

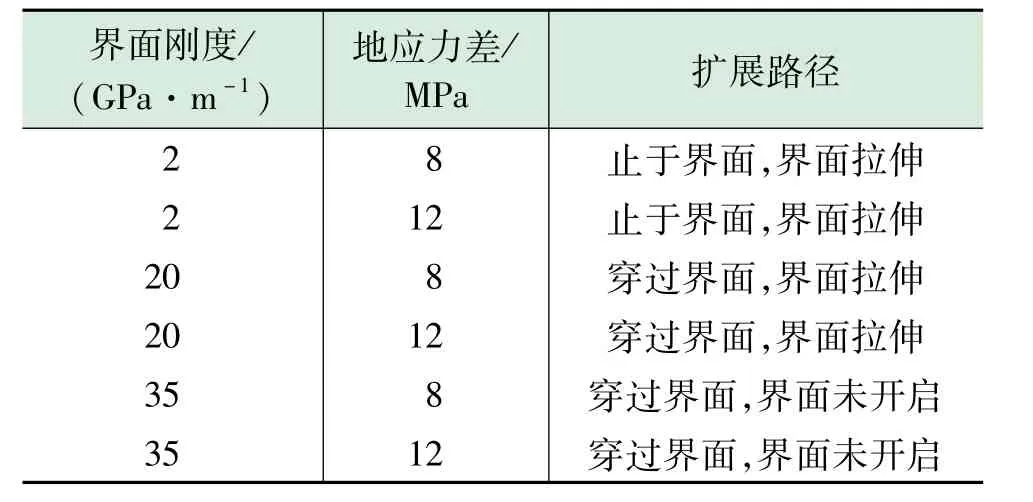
表4 不同界面刚度条件下水力裂缝界面处扩展路径

这说明，页岩层理界面强度影响着水力裂缝在界面处的扩展形式，较低的界面刚度值情况下水力裂缝将会开启页岩弱层理界面，高界面刚度情况下水力裂缝在穿过界面的同时将会开启界面；过高的界面刚度值情况下，水力裂缝将不再受到界面的影响，而是直接穿过并不开启界面，这种情况下可以在一定程度上认为不存在弱层理界面。

4.3 注液速率影响

表5为不同注液速率水力裂缝沿层理界面扩展路径，其中页岩层里界面拉伸刚度为35 GPa/m、能量释放率为70 N/m、最大拉应力为2 MPa；本体Cohesive拉伸刚度值为40 GPa/m、能量释放率为150 N/m、最大拉应力为6 MPa，计算得到水力裂缝层理界面处的扩展规律，如表5所示。

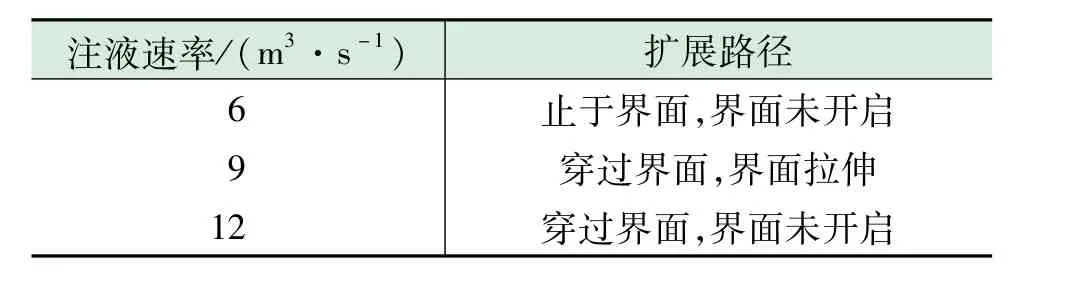
表5 不同注液速率条件下水力裂缝界面处扩展路径

由表5可以看出，注液速率影响着水力裂缝在界面处的扩展路径，当注液速率增大时，水力裂缝在界面处更容易穿过层理界面。

不同注液速率裂缝高度变化规律见图7。

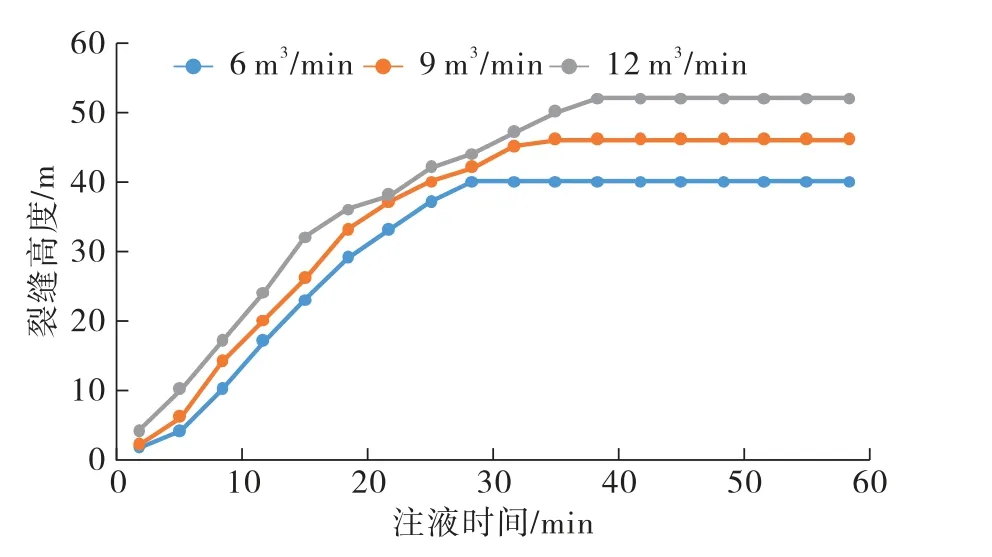
图7 不同注液速率条件下垂直裂缝高度

从图7看出，注液速率为6 m3/m时，由于裂缝未穿过界面，在28.3 min左右其裂缝在高度方向上抵达上下界面，缝高停止增长，注液速率为9 m3/m与12 m3/m时，裂缝穿过界面，缝高持续增长。

5 实例分析

以威远地区A井为例，该井所在井区层间厚度为20～40 m，且该压裂井施工段垂向应力σv与最小水平地应力σh之差达到4.1 MPa。依据数值计算结果，该种情况下裂缝在缝高方向很难开启层理，进而对A井的体积压裂复杂缝网的形成造成影响。

基于此，现场选取12 m3/min的注液排量，以增大缝内净压力。

从A井体积压裂施工后的微地震资料可以得出，水力裂缝在三维地层中扩展均匀，在高度方向上平均高度约为50 m，已经穿过地层界面，沿层理面方向（东西方向）上分布较大。

6 结论

（1）地应力差影响水力裂缝在层理界面处的扩展路径，当垂向应力与最小水平地应力差超过3 MPa时，裂缝更容易穿透层理面。

（2）页岩层理界面刚度影响水力裂缝在界面处的扩展形式，当界面刚度大于20 GPa时，水力裂缝越容易穿透水力层理而不发生偏转；当界面刚度小于20 GPa时，弱层理界面影响下的裂缝高度越小。

（3）不同的注液速率将导致不同的裂缝几何形态，注液速率超过9 m3/min时，水力裂缝穿过弱层理面的可能性较大；对于现场页岩气压裂施工，可采取增大注液排量的措施达到增大改造体积目的。