一种贝叶斯对数正态分布的张量分解插补算法

李小沛 李凡长 梁合兰

(苏州大学计算机科学与技术学院 江苏 苏州 215006)

0 引 言

智能交通系统已经被用于在各种场景中获得大量的城市交通数据。这些数据可以作为各种研究的数据集为交通管理者和研究者使用。通常可以将数据提取成矩阵存储，考虑将矩阵扩展成高维度的数据，可以保存数据本身的信息结构，高维度的数据存储形式被称作张量。所以可以将取得的数据变成一个多维数组，如按照路段×天×一天的时间间隔，或者用户×路段×某天。

虽然可以利用取得的数据进行整理分析预测，但是总会有各种外界因素，例如某地的网络信号有所浮动等故障，这会对数据的获取带来影响，最直接的结果就是使取得的时空数据有所缺陷，即数据缺失问题。如果该道路在给定的时空范围内没有任何数据信息，会使得数据集变得稀疏，导致无法准确地进行预测和估算，这会给基于这些数据集的各种工作带来负担。为了解决上述问题，就产生了对不完整数据集的缺失条目提供可靠估计的研究。

由于每个时空数据由不同含义的维度来定义，选择用张量来处理这类数据。处理稀疏张量数据的方式就是张量分解。当前较为流行的张量分解为CANDECOMP/PARAFAC模型和Tucker模型[1]。在插补任务中，考虑对未知条目的可靠预测，引入了一种贝叶斯矩阵分解算法[2]，并将其拓展为高阶张量来使用，即贝叶斯张量分解[3]。

这种完全的贝叶斯模型表征了数据生成过程，因此能够有效地估算缺失的条目。利用贝叶斯分析，在推导过程中，将共轭先验使用在超参数上，分析并得出其后验分布，得到马尔可夫链蒙特卡洛算法的采样模型[2]。MCMC算法为缺失值提供了多种估计，避免单点估计带来的较大误差[4]。由于数据集可以很好地拟合成高斯分布而没有极端值，考虑到速度数据集非负这一特性，选取一组服从对数正态分布的随机数据作为初始值，并选用了如下三种数据的表示形式[10]：(1) 矩阵(路段×时间间隔)；(2) 三阶张量(路段×天×时间间隔)；(3) 四阶张量(路段×周×天×时间间隔)。本文在这三种表示上评估了不同的模型的插补性能，发现本模型在三阶张量结构上的性能较好。

1 相关工作

张量已经是统计学问题中最为常见的数据存储形式。前人已经对张量的知识及其分解应用做了非常全面的综述，例如特征提取、数据填补、轨迹预测、数据降噪、信号处理及推荐系统方面等[6-8,15-16,24-25]。

已知的对缺失数据插补的方法中最常用的就是张量分解方法。利用观察到的数据估计低秩近似的模型，并且利用估计的低秩近似模型计算出缺失的条目[9]。

张量已经被应用在智能交通数据的研究中，例如在时空交通速度数据和轨迹预测数据集中应用张量来处理数据：文献[9]提出了一种SVD组合张量分解恢复不完全数据的方法；文献[10]提出了一种低秩张量分解模型(HaLRTC)来恢复从城市道路网收集的缺失交通速度数据集；文献[11]提出了一种基于上下文感知的张量Tucker分解的方法对收集的轨迹数据进行预测；文献[12]提出了一种基于上下文感知的将CP和Tucker分解结合的BTD方法对数据进行预测；文献[13]提出了一种Tucker分解方法来促进核心张量的简约性；文献[14]提出了一种基于动态张量进行短期交通流量预测的方法；文献[3]提出了一种贝叶斯高斯CP张量方法，基于贝叶斯推断，利用服从标准正态分布的随机变量迭代，对缺失数据集进行CP分解来进行数据集的插补。除此之外，还有很多运用张量的算法研究[15-17,21-22]，也有将张量和深度学习联合应用的研究[18-19]。

先前的研究大多数采用单点计算，在逼近过程中就会产生较大的误差，不能得出较为准确的结果。由于贝叶斯推断只需要较少的观察来进行估计，为了解决这个问题，将贝叶斯推理方法加入到张量分解问题当中，这可以有效地解决上述问题[16,20]。

2 贝叶斯对数正态分布张量分解

2.1 张量模型

几何代数中定义的张量是基于向量和矩阵的推广。简单而言，可以将标量视为零阶张量，多个标量组成的矢量视为一阶张量，多个矢量组成的矩阵视为二阶张量，多个矩阵的排列可以视为三阶张量，之后增加了维度的数据结构统称为高阶张量，空间上更为立体。为了便于张量运算，介绍以下张量分解中的数学知识。

(1) Kronecker积。Kronecker积在张量计算中十分常见，它是衔接矩阵计算和张量计算的桥梁。Kronecker积的定义为：给定一个大小为m1×m2的矩阵A，一个大小为n1×n2的矩阵B，矩阵A和B的Kronecker积为：

(1)

式中：矩阵A⊗B的大小为(m1n1)×(m2n2)；符号⊗表示Kronecker积。

(2) Khatri-Rao积。在矩阵分解过程中，利用一种特殊的矩阵运算加快采样过程，这个运算就是Khatri-Rao积(KR乘积)。其定义为：给定如下两个矩阵：

A=(a1,a2,…,ar)∈Rm×r

B=(b1,b2,…,br)∈Rn×r

(2)

矩阵A、B有相同的列数，则其KR积为：

A⊙B=(a1⊗b1,a2⊗b2,…,ar⊗br)∈R(mn)×r

(3)

式中：符号⊙表示KR积；符号⊗表示Kronecker积。

(3) 张量的秩。张量的秩与矩阵的秩的定义类似，但是有一些不同。张量的秩在实数域和复数域可以不同，并且没有直接的算法可以计算给定的张量的秩。通常情况下都是选择多个不同的值。本文分别选择了三个不同的值进行比较：r=50,80,110。

(4) CANDECOMP/PARAFAC(CP)张量分解。CP分解是将高维度的张量分解成为秩一张量的和，如图1所示。

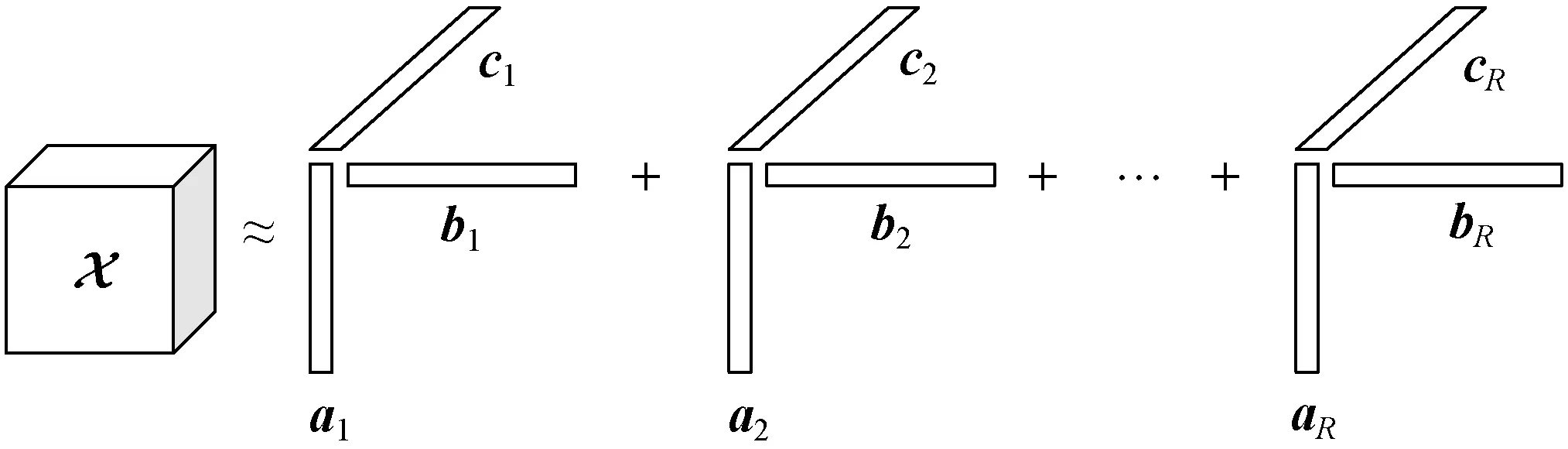
图1 张量CP分解模型

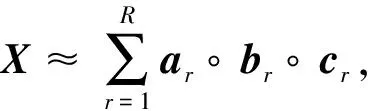
k=1,2,…,K

(4)

定义因子矩阵表示向量的组合，例如A=[a1,a2,…,aR]，然后对三维情况，可以写成如下形式：

X(1)≈A(C⊙B)T

X(2)≈B(C⊙A)T

X(3)≈C(B⊙A)T

(5)

式中:X(i)表示张量X在模式i上的展开。CP分解可以简明地表述为：

(6)

如果将A、B和C标准化，然后提出权重λ∈RR，可以得到如下表述：

(7)

对于N维度的情况：

x≈[[λ;A(1),A(2),…,A(N)]]≡

(8)

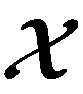
(9)

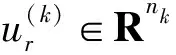
(10)

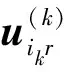
2.2 对数正态分布

正态分布，又称为高斯分布，若随机变量X服从一个位置参数为μ、尺度参数为σ的概率分布，且其概率密度函数为：

(11)

这个随机变量就可称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作：

X～N(μ,σ2)

(12)

当μ=0,σ=1时，正态分布就成为标准正态分布，记为：

(13)

但是由于有些量的值必须是正数，由于高斯分布中X中的值可正可负，所以它不能很好地描述这样的变量分布。在很多应用中，可能数据不符合正态分布，但是随机变量的对数可能符合正态分布，此情况就称之为对数正态分布，它是指一个随机变量的对数服从正态分布，则该随机变量服从对数正态分布。

若X是取值为正数的随机变量，若lnX～N(μ,σ2)，且其概率密度函数为：

(14)

则称随机变量X服从对数正态分布，记为：

lnX～N(μ,σ2)

(15)

2.3 贝叶斯对数正态分布CP分解

对多维交通数据变成的张量进行插补缺失条目的操作，利用了贝叶斯张量分解，贝叶斯分析方法是将未知参数的先验信息，与样本信息联合，根据贝叶斯公式，得出后验分布公式，而后依照后验信息推断未知参数。由于本文算法选用的数据集是速度数据集，这要求每一个值都是非负的，所以选用服从对数正态分布的随机变量作为初始值进行算法循环。

首先，假设观察到的项遵循独立的对数正态分布：

lnxi～N(μ,λ-1)

(16)

式中：μ代表是均值；λ代表精度，λ-1代表方差。假设所有的因子矩阵中的行向量的先验分布为多变量的正态分布：

(17)

多变量正态分布是单维正态分布向多维的推广。在贝叶斯环境中，使用多变量共轭Gaussian-Wishart先验来增强模型的鲁棒性，在μ和Λ都是未知的情况下，Gaussian-Wishart分布公式为：

p(μ,Λ|μ0,β0,W0,v0)=N(μ|μ0,(β0Λ)-1)W(Λ|W0,v0)

将超参数μ(k)和Λ(k)代入该公式，结果为：

(μ(k),Λ(k))～Gaussian-Wishart(μ0,β0,W0,v0)

p(μ(k),Λ(k)|μ0,β0,W0,v0)=

N(μ(k)|μ0,(β0Λ(k))-1)×Wishart(Λ(k)|W0,v0)

(18)

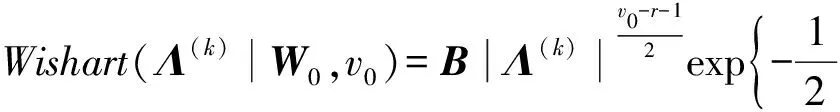
在式(16)的随机变量服从对数正态分布的假设下，方差用来捕获数据中偏离预期值的数据。然而，方差在已知的数据集中对我们而言也是未知参数。因此对精度参数使用一个单变量高斯分布，其似然函数为：

(19)

其共轭Gamma先验分布公式为：

其后验分布为：

记为：

λ～Gamma(a0,b0)

(20)

图2引用自文献[3]，展示了上述贝叶斯概率CP分解的数据生成过程的结构图。三个模型图分别对应矩阵、三阶张量和四阶张量。在此模型图中，节点xi代表观测到的数据；λ是参数；μ(k)、Λ(k)、a0和b0都是需要预先设置的超参数。当初始化采样时，应设置这些超参数。这样可以基于此模型推导出用于贝叶斯推断的Gibbs采样算法。

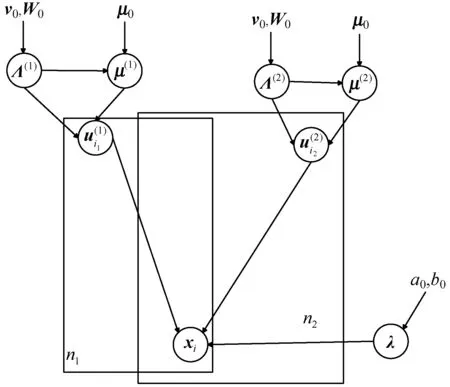
(a) 矩阵

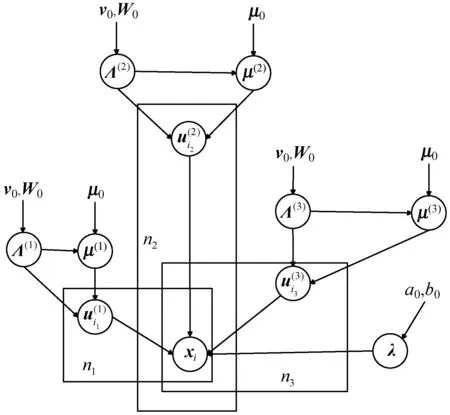
(b) 三阶张量

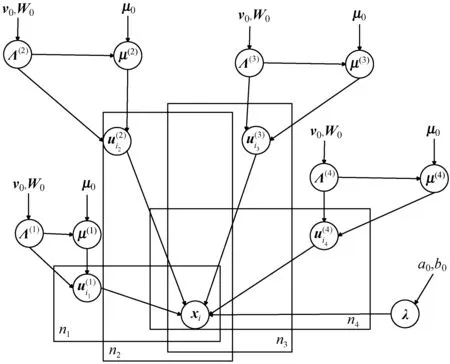
(c) 四阶张量图2 贝叶斯概率CP分解的数据生成过程的结构图

2.4 Gibbs采样

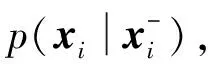
不断循环使得随机变量的概率分布将收敛于x的联合概率分布p(x)。

Gibbs采样的思想是在每次迭代中顺序更新所有变量。在所有其他变量的当前值的条件下，从其分布中采样每个变量。Gibbs采样算法的关键是为所有变量定义这种分布，这些条件分布通常称为完全条件。由于已经将共轭先验用于参数和超参数，因此图中模型的后验分布可以通过分析得出，以图2中三阶张量为例进行推导。

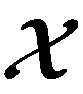
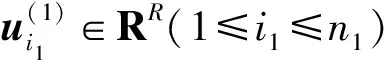
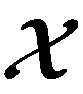
(21)

式中：⊗代表Hadamard乘积。结合式(17)和式(21)，给出后验分布多变量高斯的形式：

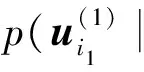
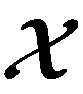
(22)

其中：

(23)

2) 采样超参数μ(k)和Λ(k)(k=1,2,3)。因子矩阵U(1)∈Rn1×R的似然函数为：

p(U(1)|μ(1),Λ(1))∝

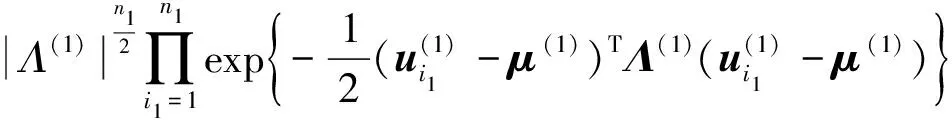
(24)

结合式(24)和式(18)中的Gaussian-Wishart超先验项，超参数μ(1)和Λ(1)的联合后验分布为：

p(μ(1),Λ(1)|U(1),μ0,W0,v0,β0)∝

p(U(1)|μ(1),Λ(1))×N(μ(1)|μ0,(β0Λ(1))-1)×

(25)

这两个分布中的参数可以通过以下方式计算：

(26)

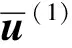
(27)

3) 采样方差的倒数λ。

似然函数为：

(28)

结合式(28)中的似然项和式(20)的先验项，可以给出λ的后验分布公式：

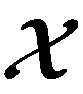
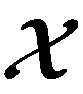
(29)

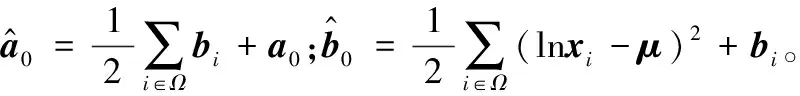
到此已经推导出三阶张量的Gibbs采样中所需要的所有变量的公式，可同样拓展至高维数据。Gibbs采样算法达到收敛后，就可以通过Monte Carlo近似估计缺失值。

通过上述对各项参数的推导和后验分布迭代公式，得出贝叶斯对数正态分布张量分解插补算法BLCP，如算法1所示。

算法1贝叶斯对数正态分布张量分解插补算法

初始化：μ0=0,β0=1,v0=r,W0=I其中I是单位矩阵，r是设置好的张量秩low rank。

设置随机变量U(k)使其服从一个对数正态分布作为初始值循环：

Foriter=1,2，…,T

Fork=1,2，…,d

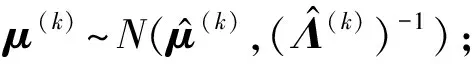
Forik=1,2,…,nk

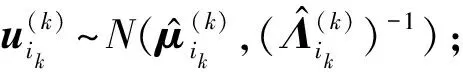
End for

End for

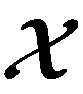
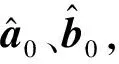
End for

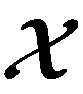
//T为迭代次数

3 实 验

本文使用的交通速度数据集是通过智能手机上广泛应用的导航程序生成的选取了文献[3]中给出的在中国广州收集的大规模交通速度数据集。数据集包含61天(2016年8月1日—2016年9月31日)，一天被划分为144个间隔(以10分钟为间隔)，并且记录了214个路段上行驶速度的观测值[3]。将这个数据集分别变成二阶、三阶和四阶张量进行实验。其中观测到的数据大约有1 855 527个，此数据集有约1.29%的数据缺失值。图3显示了观测到的速度数据的直方图，可以看出，数据的分布可以拟合成一个最大似然的高斯分布而没有极端值。

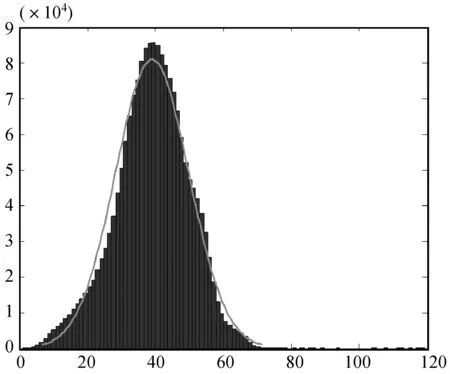
图3 观测到的速度数据直方图和正态分布的拟合

3.1 对比实验

通过随机删除一定数量的已知值来创建实验数据集，然后将原始数据集作为缺失数据的基础事实，可以利用这两个数据集评估本文算法插补的性能。

在对比实验中，对比了以下三个基于张量分解的插补方法和一个传统的方法：(1) K最近邻分类算法(KNN)；(2) 高精度低秩张量算法(HaLRTC)[10]；(3) SVD组合张量分解算法(STD)[9]；(4) 基于标准正态分布的贝叶斯张量分解方法(BGCP)[3]。

使用平均绝对百分比误差(MAPE)和均方根误差(RMSE)作为模型的评价指标，其计算公式分别为：

(30)

(31)

3.2 数据表示

张量的结构表示也是需要考虑的关键因素。基于交通速度数据集，本文使用了三种不同类型的数据表示形式[3]。

3.3 实验结果

对于随机丢失的情况，随机删除矩阵表示形式(1)中的某些条目，并将矩阵中的数据重塑为三阶张量和四阶张量的存储形式。

随机删除数据在不同模型下的性能如表1所示。由于STD模型主要解决非凸性问题，因此它在矩阵表示的数据集和四阶张量表示的数据集中没有提供太多的改进，所以只在三阶张量表示的数据集中有所应用。分别删除了原始数据集的10%、20%、30%、40%、50%，整理出五个数据集。本文模型对Gibbs采样算法进行了1 000次迭代估算缺失条目(T=1 000)。分别选取了张量秩为r=50、80、110来运行所有算法模型，最优结果已在表1中标粗。可以看出，BLCP在处理三阶张量的缺失数据集上有较好的性能。

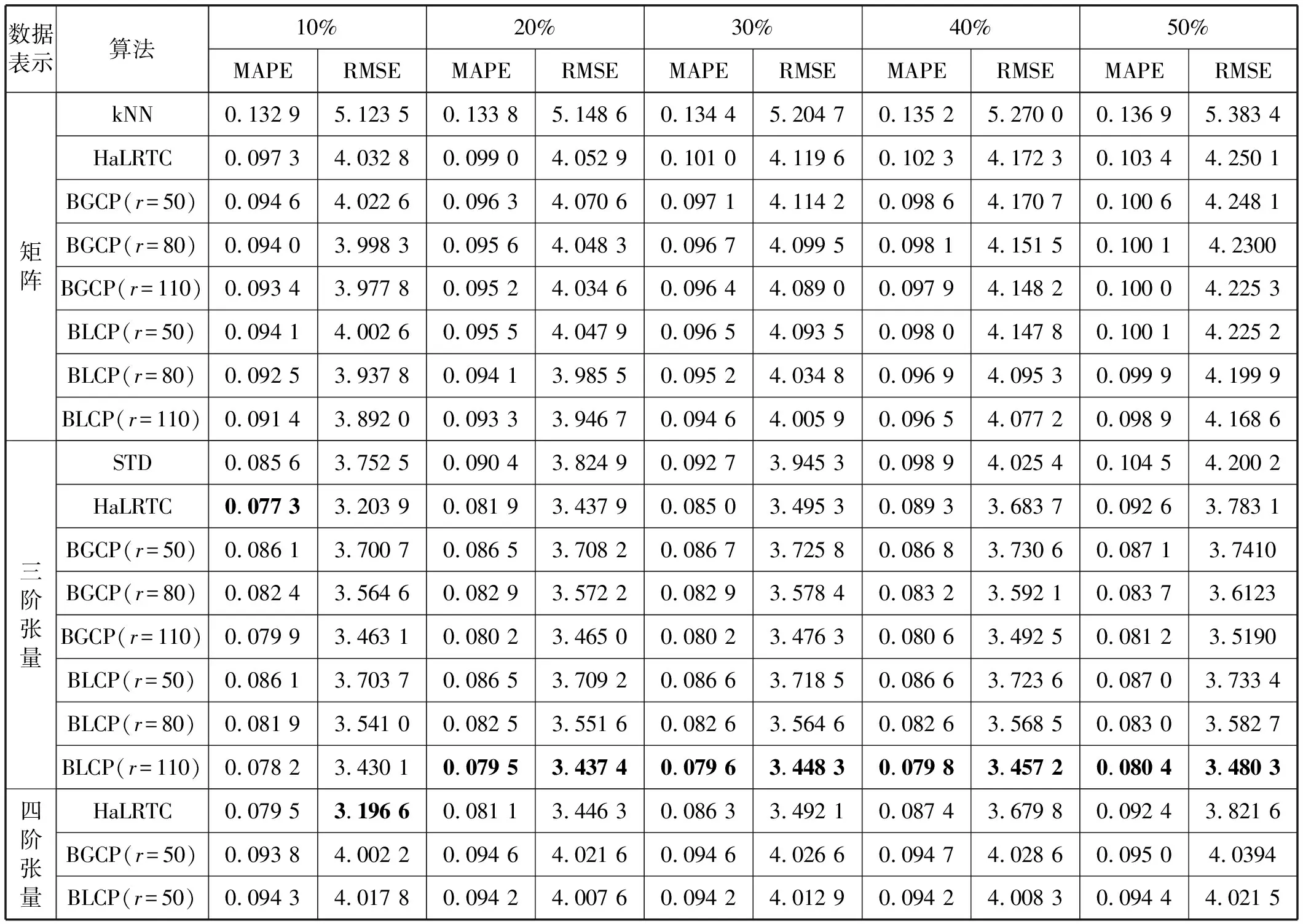
表1 实验结果

4 结 语

本文提供了一种贝叶斯对数正态分布的张量CP分解模型，对时空数据集的缺失位置进行插补任务。并利用了收集到的时空交通速度数据集作为实验数据集[3]，将数据集变成二阶张量(矩阵)、三阶张量和四阶张量三种不同的维度作为实验数据存储形式。通过随机删除二阶张量中的10%到50%的数据，并依次将其重塑成三阶张量和四阶张量作为实验数据，以原始未删除数据的数据集作为事实依据，并与HaLRTC、传统的KNN算法、STD算法及基于标准正态分布的贝叶斯高斯张量分解算法(BGCP)进行了比较，结果表明，在随机删除数据情况下，本文算法在处理三阶张量存储形式的数据上能获得较好的结果。

由于张量分解方法都是基于对低秩张量的逼近假设，并且时空数据集可能存在着强烈的时空关联性，在之后的研究可以考虑将时空关联的影响加入到算法中，并且由于CP分解张量的秩难以求出并且取得一个较好的值，可以考虑非参数的贝叶斯模型应用于CP分解上。除此之外，由于张量CP分解可能存在大量的冗余因子，可以考虑开发基于贝叶斯的Tucker算法解决上述问题。