Hom-LPNG代数的相关性质

张永平, 魏 竹, 张庆成

(1. 沈阳化工大学 理学院, 沈阳 110142； 2. 东北师范大学 数学与统计学院, 长春 130024)

Hom-型代数是在Hom-Lie代数[1]的基础上, 增加一个线性映射后得到的一类新代数, 是Hom-Lie代数的一种推广. 目前, 关于Hom-型代数的研究已有很多成果. 例如： 在一个代数体系中有Hom-Novikov代数[2-3]、 Hom-Leibniz代数[4-5]和Hom-结合代数[6-7]等； 在两个代数体系中有Hom-Novikov-Poisson代数[3]、 Hom-Novikov-Poisson超代数[8]和Hom-Gel’fand-Dorfmand代数[9-10]等. WANG等[11]在交换结合代数、 李代数、 Novikov代数的基础上定义了LPNG代数. 受上述Hom-型代数和LPNG代数的启发, 本文给出三个代数体系中Hom-LPNG代数的概念, 并给出Hom-LPNG代数的相关性质.

1 预备知识

定义1[9]设L是一个线性空间, ·:L×L→L是一个双线性映射,σ:L→L是一个线性映射, 如果下列条件成立：

x·y=y·x, ∀x,y∈L,

(1)

(x·y)·σ(z)=σ(x)·(y·z), ∀x,y,z∈L,

(2)

则称(L,·,σ)为Hom-交换结合代数.

定义2[3]设L是一个线性空间, ∘:L×L→L是一个双线性映射,σ:L→L是一个线性映射, 如果下列条件成立:

(x∘y)∘σ(z)=(x∘z)∘σ(y), ∀x,y∈L,

(3)

(x∘y)∘σ(z)-σ(x)∘(y∘z)=(y∘x)∘σ(z)-σ(y)∘(x∘z), ∀x,y,z∈L,

(4)

则称(L,∘,σ)为Hom-Novikov代数.

定义3[3]设L是一个线性空间, ·,∘:L×L→L是两个双线性映射,σ:L→L是一个线性映射, (L,·,σ)是一个Hom-交换结合代数, (L,∘,σ)为Hom-Novikov代数, 如果下列条件成立：

(x·y)∘σ(z)=σ(x)·(y∘z), ∀x,y,z∈L,

(5)

(x∘y)·σ(z)-σ(x)∘(y·z)=(y∘x)·σ(z)-σ(y)∘(x·z), ∀x,y,z∈L,

(6)

则称(L,·,∘,σ)为Hom-Novikov-Poisson代数.

定义4[9]设L是一个线性空间, [,]:L×L→L是一个双线性映射,σ:L→L是一个线性映射, 如果下列条件成立：

[x,y]=-[y,x], ∀x,y∈L,

(7)

[σ(x),[y,z]]+[σ(y),[z,x]]+[σ(z),[x,y]]=0, ∀x,y,z∈L,

(8)

则称(L,[,],σ)为Hom-Lie代数.

定义5[9]设L是一个线性空间, [,]和∘:L×L→L是两个双线性映射,σ:L→L是一个线性映射, (L,[,],σ)是一个Hom-Lie代数, (L,∘,σ)为Hom-Novikov代数, 如果下列条件成立：

则称(L,∘,[,],σ)为Hom-Gel’fand-Dorfman代数.

定义6设L是一个线性空间, [,],·,∘:L×L→L是三个双线性映射,σ:L→L是一个线性映射, 且(L,·,σ)为Hom-交换结合代数, (L,∘,σ)为Hom-Novikov代数, (L,[,],σ)为Hom-Lie代数, 如果式(5),(6),(9)及下列条件成立:

[x,y]·σ(z)=[x,z]·σ(y)+σ(x)·[z,y], ∀x,y,z∈L,

(10)

则称(L,·,∘,[,],σ)为Hom-LPNG代数.即(L,·,∘,σ)为Hom-Novikov-Poisson代数, (L,∘,[,],σ)为Hom-Gel’fand-Dorfman代数, 且运算·和[,]均满足式(10).

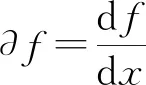
f∘g=f·∂(g), [f,g]=f·∂(g)-g·∂(f),σ(xα)=(x+c)α,

其中c∈是一个定值,α是任意正整数, 则(L,·,∘,[,],σ)为一个Hom-LPNG代数.

2 主要结果

证明： 证明分如下4步.

1) 由于

x·σy=σ(x)·σ(y)=σ(x·y)=σ(y·x)=σ(y)·σ(x)=y·σx,

(x·σy)·σσ(z)=σ(σ(x)·σ(y))·σ2(z)=σ2((x·y)·z),

σ(x)·σ(y·σz)=σ2(x·(y·z))=σ2((x·y)·z),

即(x·σy)·σσ(z)=σ(x)·σ(y·σz), 因此式(2)成立.于是(L,·σ,σ)是一个Hom-交换结合代数.

3) 由于

(x·σy)∘σσ(z)=σ(σ(x)·σ(y))∘σ2(z)=σ2((x·y)∘z),

σ(x)·σ(y∘σz)=σ2(x·(y∘z)),

因此式(5)成立.又由于

(x∘σy)·σσ(z)-σ(x)∘σ(y·σz)=σ2((x∘y)·z)-(x∘(y·z)),

(y∘σx)·σσ(z)-σ(y)∘σ(x·σz)=σ2((y∘x)·z)-(y∘(x·z)),

因此式(6)成立.于是(L,·σ,∘σ,σ)是一个Hom-Novikov-Poisson代数.

4) 由于

故式(10)成立.

命题2设(L,·,∘,[,])是一个LPNG代数,σ为(L,·,∘,[,])的一个自同态.如果定义运算·σ,∘σ,[,]σ如下:

x·σy=σ(x)·σ(y),x∘σy=σ(x)∘σ(y), [x,y]σ=[σ(x),σ(y)],

则(L,·σ,∘σ,[,]σ,σ)为一个Hom-LPNG代数.

证明: 由命题1知(L,·σ,σ)是一个Hom-交换结合代数, (L,∘σ,σ)是一个Hom-Novikov代数, (L,·σ,∘σ,σ)是一个Hom-Novikov-Poisson代数.由文献[9]中定理3.5知, (L,∘σ,[,]σ,σ)是一个Hom-Gel’fand-Dorfman代数, 因此只需证明式(10)成立即可.由于

[x,y]σ·σσ(z)=σ2([x,y]·z),

[x,z]σ·σσ(y)+σ(x)·σ[z,y]σ=σ2([x,z]·y+x·[z,y]),

故式(10)成立.

综上, (L,·σ,∘σ,[,]σ,σ)为一个Hom-LPNG代数.

命题3设(L,·,σ)为一个交换Hom-交换结合代数,F是特征数为0的域.∀λ∈F, ∂是L的一个导子, 且∂σ=σ∂.如果定义运算∘和[,]如下:

x∘y=x·∂(y)+λx·y, [x,y]=x·∂(y)-y·∂(x),

则(L,·,∘,[,],σ)为一个Hom-LPNG代数.

证明: 证明分如下4步.

1) 由文献[9]中推论3.9知, (L,∘,σ)是Hom-Novikov代数.

2) 由于

(x·y)∘σ(z)=(x·y)·∂(σ(z))+λ(x·y)·σ(z)=σ(x)·(y·∂(z))+λσ(x)·(y·z),

σ(x)·(y∘z)=σ(x)·(y·∂(z)+λy·z)=σ(x)·(y·∂(z))+λσ(x)·(y·z),

因此式(5)成立.又由于

(y∘x)·σ(z)-σ(y)∘(x·z)=-σ(y)·(x·∂(z))=-(y·x)·σ(∂(z))=-σ(x)·(y·∂(z)),

因此式(6)成立.于是(L,·,∘,σ)是Hom-Novikov-Poisson代数.

3) 由文献[9]中定理3.9知, (L,∘,[,],σ)是Hom-Gel’fand-Dorfman代数.

4) 由于

故式(10)成立.

综上, (L,·,∘,[,],σ)是一个Hom-LPNG代数.

例2若将例1中∘定义为f∘g=f·∂(g)+λx·y(λ是一个固定数), ·和[,]定义不变, 则由命题3知, 新代数(L,·,∘,[,],σ)为一个Hom-LPNG代数.

命题4设(L,·,σ)为一个交换Hom-交换结合代数, 且σ2=σ, ∂是L的一个导子, ∂σ=σ∂.如果定义运算∘和[,]如下:

x∘y=σ(x·∂(y)), [x,y]=σ(x·∂(y))-σ(y·∂(x)),

则(L,·,∘,[,],σ)为一个Hom-LPNG代数.

证明: 证明分如下3步.

1) 由文献[9]中推论3.10知, (L,∘,σ)是Hom-Novikov代数, (L,∘,[,],σ)是一个Hom-Gel’fand-Dorfman代数.

2) 由于

(x·y)∘σ(z)=σ((x·y)·∂(σ(z)))=(σ(x)·σ(y))·σ2(∂(z))=σ2(x)·(σ(y)·σ(∂(z))),

σ(x)·(y∘z)=σ(x)·σ(y·∂(z))=σ(x)·(σ(y)·σ(∂(z))),

且σ2=σ, 所以式(5)成立.又由于

(y∘x)·σ(z)-σ(y)∘(x·z)=-σ(x·(y·∂(z)))=-σ(y·(x·∂(z))),

故式(6)成立.因此(L,·,∘,σ)是Hom-Novikov-Poisson代数.

3)由于

[x,y]·σ(z)=(σ(x·∂(y))-σ(y·∂(x)))·σ(z)=σ((x·∂(y))·z-(y·∂(x))·z),

故式(10)成立.

综上, (L,·,∘,[,],σ)是一个Hom-LPNG代数.

例3A是以{e1,e2}为生成元的二维空间, 定义其上的一个双线性运算*为e1*e1=e1,e1*e2=e2*e1=0, 且A上的同态映射σ1(e1)=e1-e2,σ1(e2)=0, 则(A,*,σ1)是一个Hom-结合代数[7], 且显然A是交换的.

令L={f|f=(kie1+kje2)xα,i,j,α∈}是一个以A为系数的x幂的代数, 其中x>0, 定义L上的运算如下:

则由命题4知(L,·,∘,[,],σ)是一个Hom-LPNG代数.

命题5设(L,·,∘,[,],σ)是一个Hom-LPNG代数, 如果存在ξ∈L, 使得σ(ξ)=ξ, 定义运算*为x*y=ξ·x·y, 则(L,*,∘,[,],σ)是一个Hom-LPNG代数.

证明: 证明分如下3步.

1) 由于x*y=ξ·x·y=ξ·y·x=y*x, 因此式(1)成立.又由于

故式(2)成立.因此(L,*,σ)是一个Hom-交换结合代数.

2) 由于

故式(5)成立.又由于

故式(6)成立.因此(L,*,∘,σ)为Hom-Novikov-Poisson代数.

3) 由于

故式(10)成立.

综上, (L,*,∘,[,],σ)是一个Hom-LPNG代数.

命题6设(L,·,∘,[,],σ)是一个Hom-LPNG代数, 定义一个新运算[,]-为[,]-=x∘y-y∘x, 则(L,·,∘,[,]-,σ)是一个Hom-LPNG代数.

证明: 由文献[9]中定理3.2知(L,[,]-,σ)是Hom-Lie代数, (L,∘,[,]-,σ)是一个Hom-Gel’fand-Dorfman代数.下面只需证明式(10)成立.由于

因此式(10)成立.

综上, (L,·,∘,[,]-,σ)是一个Hom-LPNG代数.

命题7(L,·,∘,[,],σ)是一个Hom-LPNG代数, 如果存在ξ∈L, 使得σ(ξ)=ξ, 定义新运算*和[,]为x*y=ξ·x·y, [,]-=x∘y-y∘x, 则(L,*,∘,[,]-,σ)是一个Hom-LPNG代数.

证明: 由命题5知, (L,*,σ)是一个Hom-交换结合代数, (L,*,∘,σ)是一个Hom-Novikov-Poisson代数; 由命题6知, (L,[,]-,σ)是一个Hom-Lie代数, (L,∘,[,]-,σ)是Hom-Gel’fand-Dorfman代数.下面只需证式(10)成立.由于

因此式(10)成立.

综上, (L,*,∘,[,]-,σ)是一个Hom-LPNG代数.