防蒸发浮球在规则波作用下的运动响应分析
潘建旭
(新疆水利水电勘测设计研究院,新疆 乌鲁木齐 830052)
1 引言
近几年来,随着“一带一路”倡议的推进及西部大开发战略的实施,西部地区经济发展水平得到稳步提升[1],但西北地区气候干旱降水稀少,水资源分布不均且开发利用难度大。为提高水资源利用率,抑制水面蒸发的重要性不言而喻[2]。在抑制水库水面蒸发方面目前较为成熟的是浮球覆盖防蒸发,研究发现浮球抑制水面蒸发效果显著,已在美国加州的马尔水库成功的运用[3]。西北地区以新疆吐鲁番市胜金乡胜金沟三期水土保持水库为例,平均5级以上大风占全年的6.6%,平均风速为1.6 m/s~5.4 m/s[4]。防蒸发浮球长期处于水环境中,不可避免地要受到波浪的作用,波浪的方向、周期和波高在自然环境中随机且不断变化,在不同大小的波浪力作用下浮球因自身稳定性差容易发生不规则的运动,将润湿部分暴露在自然环境中,使其蒸发抑制率严重下降[5]。
目前物理模型试验和数值模拟试验是研究波浪与浮体相互作用的主要方法。但传统的物理实验在能直观反映浮体运动的同时具有成本高、耗时长、尺寸限制等缺点。近年来随着计算机技术的不断完善与发展,数值模拟技术已越来越成熟,其中以数值造波为核心建立数值波浪水槽[6],其本质上是通过计算机仿真模拟程序代替传统物理水槽模型,最终完成相应的科学研究任务。通过数值模拟技术可以避免传统物理模型试验的部分局限性,极大地提高了在波浪作用下对浮体运动响应的研究效率[7]。1977年Faltinsen[8]对浮体在波浪场中的运动进行了模拟,但由于早期的技术所限,并没有获得特别精确的模拟结果;周华伟[9]和吴国雄基于线性势流理论,研究了波浪与含“月池”浮体的相互作用问题;1993年王永学[10]通过求解N-S方程,在二维水槽中模拟了波在向前推进时的传播、变形、破碎、倾覆等过程;2003年齐鹏[11]等人在三维数值波浪水池中,计算出波浪对固定长方体浮体结构上的波浪力;2009年张婷[12]应用Flow-3D计算仿真工具在三维水槽中模拟波浪与小尺度及大尺度结构物的相互作用;2014年张涛涛[13]利用Flow-3D对造波和数值水槽的构建方法进行了比对分析;王元战[14]利用Flow-3D研究波浪冲击荷载与高桩码头上部结构的关系;陈兆虎[15]基于Flow-3D建立波浪水槽分析结构断面所受波浪力及波动压强分布特点。
本文以RNGk-ε模型、有限差分法和VOF方法为基础,利用FAVOR技术显示几何体,采用计算仿真工具软件Flow-3D,建立波浪水槽数值模型并验证,通过对浮球在不同波高和周期的波浪作用下速度、升沉等数据进行分析,对浮球在波浪作用下的运动响应规律进行模拟研究,为提高干旱区平原水库防蒸发浮球的稳定性和节水效率提供理论基础。
2 数值模型
2.1 数值方法
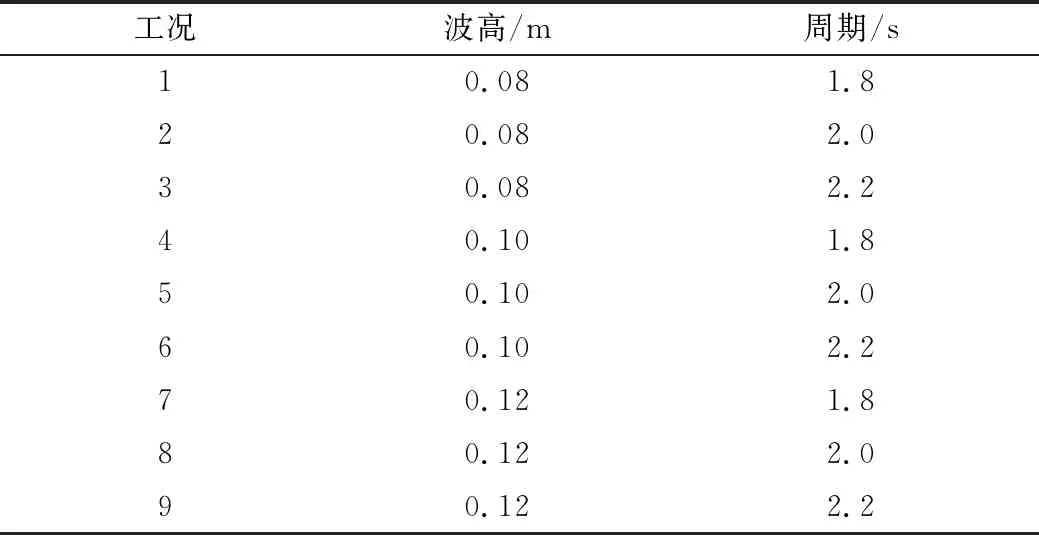
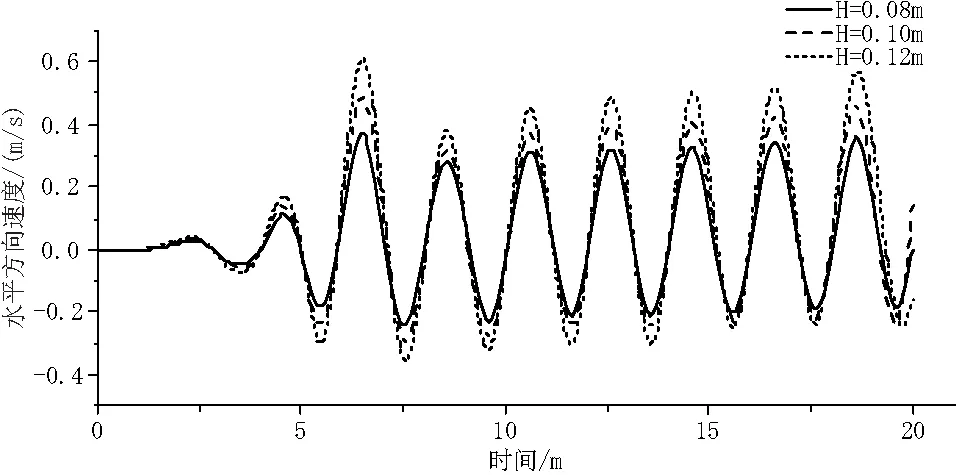
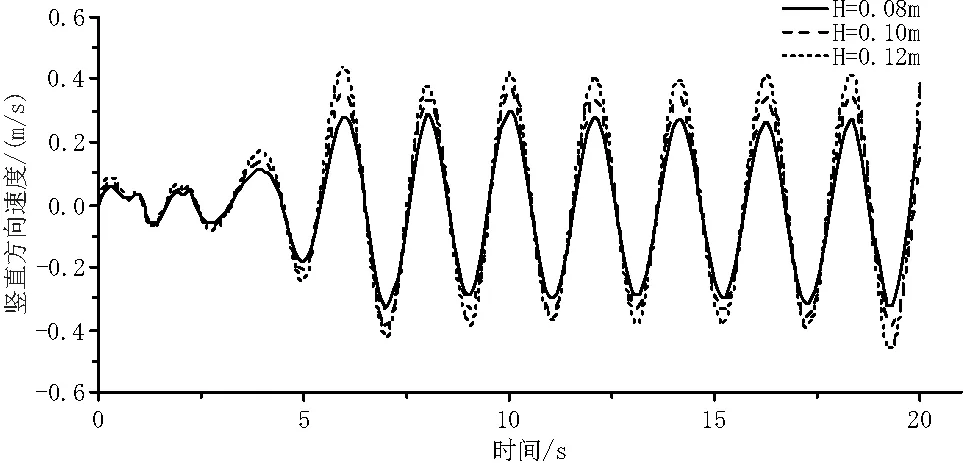
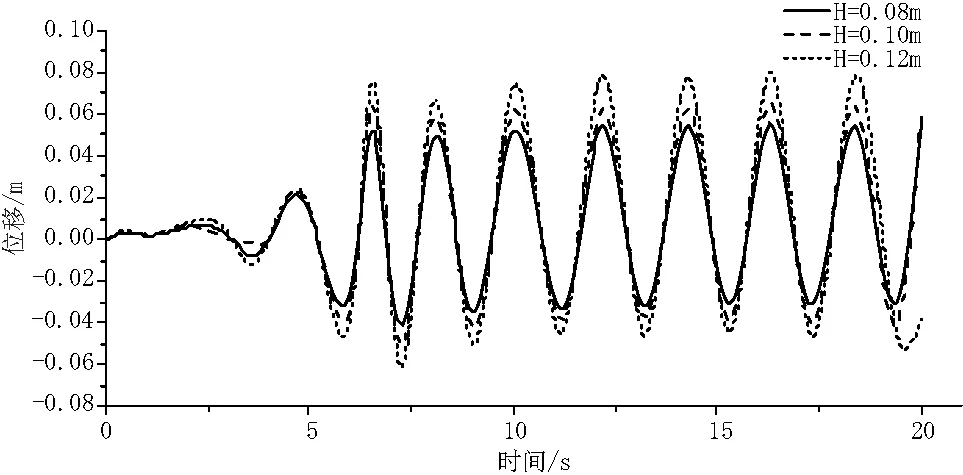
数值模型采用湍流模型,自由液面的捕捉运用VOF法。VOF法简单易行、存储量小、精度高、追踪的界面清晰。在计算域中定义一个流体体积函数F,表示单元内随时间、空间变化的流体所占有的体积与该单元可容纳流体体积之比,若单元内没有任何流体,则F=0;若单元被流体全部占满,则F=1;若该单元为交界面单元,则0 针对基本的流体运动都采用连续性方程和黏性不可压缩流体的N-S方程,连续性方程为流体控制方程。 连续性方程: (1) 动量方程: (2) VOF方程: (3) 式中:P为大气压强;ρ为流体的密度;VF为可流动流体的体积分数;U、v、w分别为x、y、z三个方向的速度分量;Ax、Ay、Az分别为三个方向上可流动流体的面积分数;Gx、Gy、Gz分别为物体三个方向的重力加速度;fx、fy、fz分别为三个方向上流体的粘滞力加速度。 造波边界定义为wave,采用线性波理论的速度入口法,模型左边界为造波边界条件,边界条件设置可给定波浪边界条件及波浪要素,即可生成线性规则波。 出流界为outflow(自由出流边界条件),出流边界满足能消除小振型线性波的So mmerfeld辐射条件。为保证在计算时间内反射波浪不会对浮球运动产生影响,模型中将浮球后方的数值水槽沿波浪传播方向加长。 水槽两侧为对称边界,边界上流体通量为零,法向方向、法向梯度与切向应力均为零。 模型底部采用无滑移边界,该边界上速度为零;顶部为液体自由面边界,其面上法向速度为零。 初始时刻,设置计算域中自由液面为静水面,水体初速度为零,压强满足在水深方向上静水压强分布。 图1 二维数值波浪水槽边界设置示意图 FAVOR网格处理技术确定结构在划分正交结构化网格中用于计算的形状。模拟波浪数值水槽中,造波端位于水槽中波浪传播方向左侧,水槽长度在波浪水平传播方向上长度取值满足计算时间内反射波未传递至浮球附近,此外为了更好地反应浮球受波浪作用的影响,减少波高衰减的影响,故在波高范围内的自由液面上下添加1个嵌套网格,对波高范围内进行网格加密,以便准确检测自由液面的波动情况。 模拟浮球在波浪场中的运动情况是通过在波浪水槽建立物体模型来实现,将浮球看作刚体[16],在其重心处建立坐标系,根据牛顿第二定律,两种运动方程为: (4) (5) 式中:m为刚体质量;F为刚体所受合外力;VG为重心处速度;TG为浮球所受关于重心的惯性矩;ω为角速度;[J]为刚体质量惯性矩。 根据模型数值理论张婷[12]等人研究,设置水槽模型水平方向长为20 m,高2 m,平均水深为1 m,建立二维数值水槽。波要素设置为波高0.2 m,周期2 s,波长为5.0 m,模拟的时间为30 s,设定记录数据的间隔为0.02 s,计算时间为20 s。分别选取波浪稳定后在x=8 m处自由液面的波动模拟结果与理论结果进行对比,其对比结果见图2。由波浪时程曲线对比模拟值与理论值可以发现,波浪在5 s之前还未稳定,在5 s~19 s范围内波浪趋于稳定,理论值和模拟值的波高、周期趋于一致,水槽模拟结果基本满足要求。 图2 x=8 m处波浪模拟值与理论值对比 本实验地点在新疆吐鲁番市胜金乡胜金台三期水土保持水库,在实验水库投入4万个直径为0.1 m的PVC浮球,入水深度为0.026 m。结合现场试验情况,设置二维数值波浪水槽中浮球直径为0.1 m,入水深度为0.026 m;根据流体、波浪理论,选择三种不同的周期和波高的规则入射波,周期分别为0.08 s、0.10 s、0.12 s,波高分别为0.08 m、0.10 m、0.12 m。在波浪载荷的作用下,浮球分别在相同周期和波高下进行单自由度运动响应,分析波浪因素对浮球运动变化的影响。工况见表1。 表1 不同工况组合 选取工况2、工况5、工况8,入射波浪为规则波,选取波高0.08 m、0.10 m、0.12 m,保持周期及其他环境参数不变,研究浮球运动速度和升沉位移的变化情况。 3.2.1 浮球水平及竖直方向速度变化 如图3(a)、图3(b)所示,其中横坐标t表示运动时间,即边界入射波的时间,纵坐标分别为随着波浪运动浮球在X、Y方向上的运动速度,速度为矢量,X、Y正方向分别为波浪行进方向和高于水平面方向。波高对浮球数值计算结果的影响:浮球随着波高的增加,X、Y方向速度随之增加。从图3(a)可以看出:当t<5 s,稳定的入射波未传到浮球,浮球速度、位移小幅波动;当t>5 s时,波浪趋于稳定,持续作用于浮球,在同一周期的波作用下,浮球X、Y方向正负速度变化趋于稳定,X方向正速度大于负速度,Y方向正负速度大致相等,浮球向波浪行进方向移动。 3.2.2 浮球升沉位移变化 从图3(c)反映了浮球在不同波高的波浪作用下的升沉位移变化,其中横坐标t,表示运动时间,即边界入射波的时间,纵坐标为浮球的升沉位移。波高对浮球数值计算结果的影响:随着波高的增大,升沉位移也随之增大。波高对浮球升沉位移影响显著,波高越大浮球的升沉位移越大,这与浮体的运动响应规律相符合。浮球在波浪的直接作用下做升沉位移,且位移随波高的增大而增大。 a浮球水平方向速度曲线图 b浮球竖直方向速度曲线图 c浮球升沉位移曲线图 选取工况4、工况5、工况6,入射波浪为规则波,选取波浪周期T为1.8 s、2.0 s、2.2 s,保持波高及其他环境参数不变,研究浮球运动速度和升沉位移的变化情况。 3.3.1 浮球水平及竖直方向速度变化 如图4(a)、图4(b)所示,其中横坐标t表示运动时间,即边界入射波的时间,纵坐标分别为随着波浪运动浮球在X、Y方向上的运动速度,速度为矢量,正负方向关系同3.2.1一致。周期对浮球数值计算结果的影响:浮球随着周期的增加,X、Y方向速度随着减小,周期越小速度变化幅度越大。从图4(a)可以看出:当t<5 s,稳定的入射波未传到浮球,浮球速度、位移小幅波动;当t>5 s后,波浪趋于稳定,持续作用于浮球,在同一波高的波作用下,浮球X、Y方向正负速度变化趋于稳定,X方向正速度大于负速度,Y方向正负速度大致相等,浮球向波浪行进方向移动。 3.3.2 浮球竖直方向升沉位移变化 从图4(c)反映了浮球在不同周期的波浪作用下的升沉位移变化,其中横坐标,表示运动时间,即边界入射波的时间,纵坐标为浮球的升沉位移。波浪周期对浮球数值计算结果的影响:随着周期的增大,升沉位移也随之增大。周期对浮球升沉位移影响显著,周期越大浮球的升沉位移越大。浮球在波浪的直接作用下做升沉位移,且位移随周期的增大而增大。 (a)浮球水平方向速度曲线图 (b)浮球竖直方向速度曲线图 (c)浮球升沉位移曲线图 选取工况5,入射波浪为规则波,波高为0.1 m,波浪周期t=2.0 s,其他环境参数不变,研究浮球运动速度的变化情况。 图5 水平及竖直方向速度对比 数值计算结果见图5,在相同周期和波高条件下模拟分析,波浪趋于稳定后,X与Y方向速度变化趋势基本一致。当X方向速度趋近为0时,Y方向速度达到极值;当Y方向速度趋近于0时,X方向的速度也达到极值。由于波浪持续作用,浮球X方向正速度大于负速度,Y方向正负速度大致相等。 本文建立了波浪作用下防蒸发浮球的运动数值模型,对浮球不同波高和周期的规则波作用下运动速度和升沉位移进行了数值模拟分析,为提高防蒸发浮球的稳定性和蒸发抑制率提供理论依据。主要结论如下: (1)当波高相同周期不相同时,浮球在波浪作用下水平与竖直方向速度随周期增大而减少。 (2)当周期相同波高不相同时,浮球在波浪作用下水平与竖直方向速度随波高增大而增大。 (3)当波高和周期条件相同时,浮球在波浪作用下运动速度也随之变化。水平方向正速度大于负速度,竖直方向正负速度大致相等;浮球水平速度为0时竖直方向速度达到极值,竖直方向速度为0时水平方向速度达到极值。 (4)当波高和周期条件变化时,浮球在波浪作用下升沉位移也随之变化。波高和周期变化越快,升沉位移变化趋势越明显。2.2 控制方程
2.3 边界条件及初始条件

2.4 模型网格划分
2.5 模型计算
2.6 模型参数及验证

3 模型计算结果分析
3.1 数值模型及工况
3.2 波高对浮球运动的影响
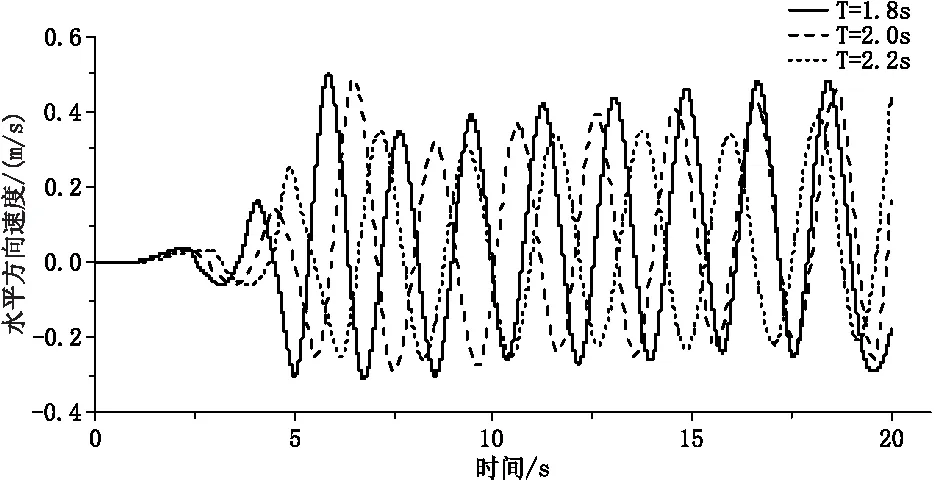
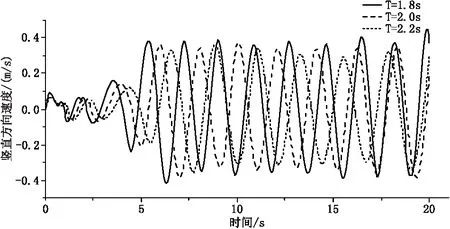
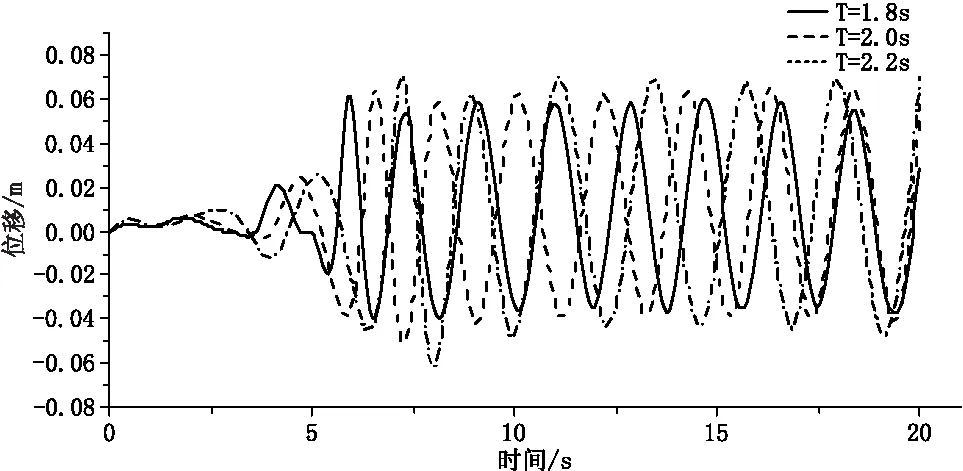
3.3 周期对浮球运动的影响
3.4 浮球水平速度与竖直速度的关系
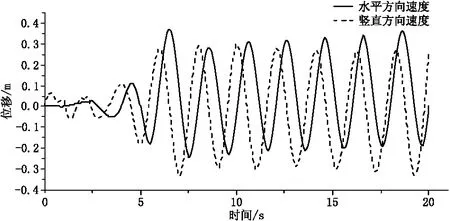
4 结语

