基于机器学习方法的三维粒子重构技术

朱浩然高 琪王洪平廖相巍赵 亮魏润杰王晋军

1．浙江大学 航空航天学院,杭州 310027;2．中国科学院力学研究所,北京 100190;3．鞍钢集团钢铁研究院 冶金工艺研究所,辽宁 鞍山 114009;4．海洋装备用金属材料及其应用国家重点实验室,辽宁 鞍山 114009;5．北京立方天地科技发展有限责任公司,北京 100083;6．流体力学教育部重点实验室 北京航空航天大学,北京 100191

0 引 言

粒子图像测速技术(Particle Image Velocity,PIV)是一种应用广泛的速度测量技术,对于复杂流体流动,可以根据体PIV中三维三分量(3D3C)流动结构进行研究。在所有的3D3C测量方法中,Elsinga等[1]提出的层析PIV技术(Tomographic PIV,Tomo-PIV)已经被证明能够在相当高的粒子播种密度(每像素0．05个粒子)下进行精确的空间分辨率测量。粒子重构(Particle Reconstruction,PR)是Tomo-PIV的关键步骤,它是解决从二维粒子图像到三维粒子分布的逆投影问题的过程。在Elsinga等[1]的Tomo-PIV原始文章中,提出了基于倍增代数重构技术(Multiplicative Algebraic Reconstruction Technique,MART)的三维粒子重构方法。从那时起,许多先进的技术被陆续开发出来用来优化三维粒子重构,以提高重构精度或效率,这已经被Scarano[2]和高琪等[3]充分验证。大多数可用的粒子重构技术都是基于MART算法的,例如空间滤波MART(Spatial Filtering MART,SFMART),它在每次MART迭代后对重构的粒子强度场进行空间滤波(Discetti等)[4]。SF-MART算法比传统的MART算法具有更好的重构质量,该算法将在本文中用来与新技术进行测试和比较。

对于粒子重构问题,随着粒子播种密度的增加,在视线交叉处会产生虚假粒子,重构质量将急剧下降。在高粒子浓度情况下,为了提高重构质量,目前已经有很多算法。Worth和Nickels[5]将乘性第一猜测(Multiplicative First Guess,MFG)作为标准MART方法的先验条件,它可以提供一个相当精确的解作为MART迭代的初始条件,并加快收敛速度。Atkinson和Soria[6]进一步提出了一种乘性LOS(Multiplicative LOS,MLOS)估计来确定可能的粒子位置,而不需要加权矩阵作为MFG。MLOS除了具有良好的初始化水平外,还可以有效去除虚假粒子从而显著提高重构质量。通过分析峰值强度和轨迹长度的联合分布,可以在某些情况下成功分离虚假粒子和实际粒子(Elsinga和Toggoz)[7]。de Silva等[8]提出的基于模拟匹配的重构增强(Simulacrum Matching-based Reconstruction Enhancement,SMRE)

技术利用实际粒子的特征形状和大小来去除重构强度场中的虚假粒子。抖盒子(Shake-The-Box,STB)方法(Schanz等)[9-10]使用已知轨迹来预测粒子分布。Wieneke[11]提出的体积粒子分布(Iterative Reconstruction of Volumetric Particle Distribution,IPR)迭代重构来校正粒子位置。与MART相比,STB在精确度和粒子浓度方面都有很大的提高。对于时间分辨图像采集,Lynch和Scarano[12]提出的序列运动跟踪增强MART方法(Sequential Motion Tracking Enhancement MART,SMTE-MART)通过建立在前一时刻的对象进行重构,也得到了一个基于增强猜测的时间推进估计目标强度场。与MART和MTE-MART相比,该方法具有更高的重构质量和更高的速度场测量精度(Novara等)[13]。对于三维粒子场重构,有学者提出了一些新的重构方案。强度增强MART方法(Intensity-Enhanced MART,IntE-MART)使用基于直方图的强度降低来抑制重影的强度(王洪平等)[14]。Gesemann等[15]使用基于约束最小二乘策略和L1正则化的优化算法求解体积强度。叶志坚等[16]提出了一种用于粒子重构的双基追踪方法,该方法在二维模拟实验中与MART相比具有更高的重构质量。Bajpayee和Techet[17]提出了一种基于单应匹配合成孔径重聚焦的高效方法。Ben Salah等[18]提出了一种“面向对象”的方法,称为基于标记点过程的迭代检测对象体积重建方法(Iterative Object Detection-Object Volume Reconstruction based on Marked Point Process,IOD-OVRMPP),用于粒子群总体的三维重构,用这种方法可以直接得到粒子的位置。

当前一些传统的粒子重构方法虽然已经取得比较理想的效果,但是在粒子重构过程中还存在一定的虚假粒子,影响粒子重构质量。随着机器学习在图像处理领域的发展,设计一个基于机器学习的模型来处理与图像相关的各种问题已成为一个热门话题。近几年来,神经网络已开始应用于粒子图像测速。机器学习已经被用来代替传统的互相关算法进行密集粒子运动的速度场估计(蔡声泽等)[19-20]。在第13届粒子图像测速国际研讨会上介绍了一系列工作。例如,Lagemann等[21]将卷积神经网络(CNN)应用于PIV,取得了与传统互相关算法相似的效果。然而,目前将机器学习应用于PIV的研究大多还处于二维阶段,将机器学习作为一种完全三维的应用用于粒子重构还缺乏研究。本文利用3D-CNN设计了一个机器学习算法来解决三维粒子重构问题,并尝试进一步提高粒子重构质量,该算法称为AI-PR(Artificial Intelligence Particle Reconstruction)。

1 卷积神经网络的概念

卷积神经网络(CNN)是人工神经网络(Artificial Neural Network,ANN)的一种,作为计算机视觉技术的有力工具已经得到了广泛的应用[22-23]。一般来说,一个深度神经网络由多层(包括输入、输出和隐藏层)组成,并且有许多可训练的参数。原始信息(如图像)通过输入层输入到CNN,预测结果(如分类结果)通过输出层给出。所有的信息通过网络内部的隐藏层进行传输和处理。神经网络的应用层一般包括卷积层、池化层、激活层和反卷积层等。

其中,卷积层是卷积神经网络结构的核心模块,其中输出的每个神经元(yj)仅连接到输入的一小部分神经元(xj),如图1(a)所示。相反,在全连接层中,任何输出神经元(yj－1)与每个输入神经元之间存在连接,如图1(a)中的黄色虚线箭头所示。因此,卷积层的正向计算通常更有效,涉及的可训练参数更少。输入和输出之间的关系可以被表示为Y＝WX＋b,输入向量X＝(x1,x2,．．．,xi)T,输出向量Y＝(y1,y2,．．．,yj)T,对于卷积层,权重矩阵W是稀疏的。

图1(a)中的局部连接性本质上是由卷积运算确定的,图1(b)中用一个简单的例子说明了卷积计算的原理(b＝0)。灰色立方体为过滤器或卷积核,其大小为3×3×4,其深度始终与输入层相同(输入层为5×5×4的蓝色立方体)。卷积核以一定的步幅(这里取1)在水平和垂直方向上移动,并将相应的输入元素乘以3×3×4卷积核内相应的系数。然后,将36组系数的乘积相加,所得的总和作为相应位置的输出值(青色正方形)。输出立方体的深度等于卷积核数,为便于说明,示例中卷积核数设为1,也可以使用多个卷积核来从输入中提取更多的特征。在卷积神经网络中,卷积核是需要学习的未知量。

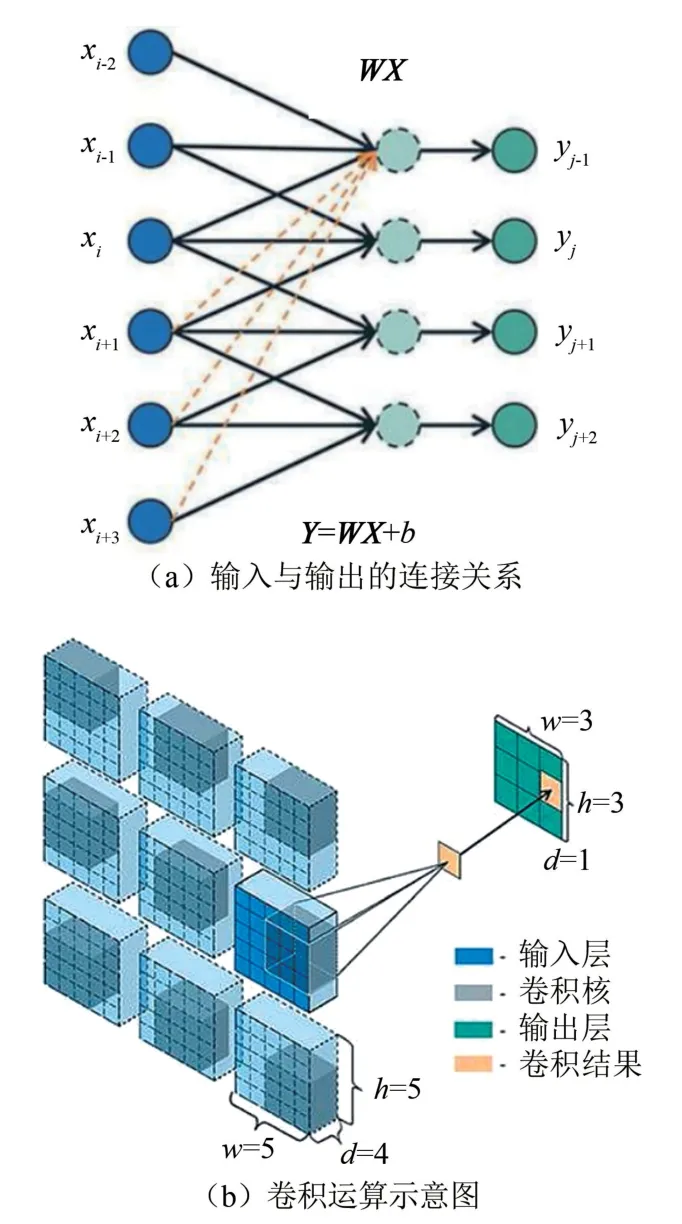
图1 简单卷积层示意图Fig.1 Sketch of the Simple convolutional layer

一旦卷积神经网络结构建立起来,就可以通过基于梯度下降的技术,通过最小化损失来训练网络的参数。由于训练数据量往往很大,为了提高训练效率,需要采用特殊的优化算法(与经典的参数优化问题相比),例如:小批量梯度下降、动量梯度下降[24]、均方根支柱(RMSprop)[25]、自适应矩估计(Adam)[26]等,这些算法已在卷积神经网络中得到了广泛的应用并取得了良好的效果。

2 使用机器学习方法进行粒子重构

神经网络的训练主要使用合成的三维粒子场作为“真实粒子场”和将其投影成多个二维图像后再使用MLOS方法重构出的三维粒子场作为神经网络的训练集。其中,MLOS方法被认为是一种非常高效的粒子场初始猜测方法,将其作为神经网络的输入可以提高计算的效率和成功率。通过多次迭代训练,获取MLOS粒子场和真实粒子场二者之间的虚拟映射关系。通过输入MLOS重构的初始三维粒子场,利用机器学习方法在训练过程中学习到的映射关系,得到接近“真实粒子场”的结果(如图2所示)。即本文提出的方法主要通过两个步骤来获得最终的粒子场。第一步通过相机成像从多个二维粒子图像中计算出初始三维粒子场(EMLOS),这与传统的PR算法相同。第二步用EMLOS作为输入,使用训练好的粒子重构的卷积神经网络计算得到最终的粒子三维分布。

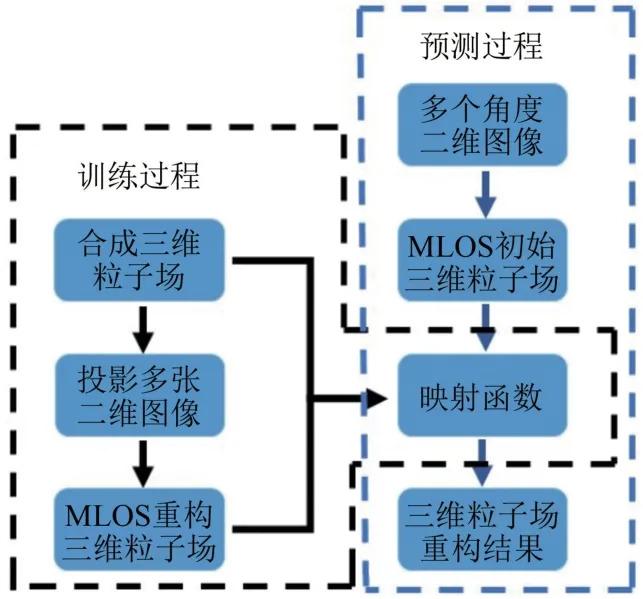
图2 机器学习方法训练和预测示意图Fig.2 Schematic diagram of machine learning method training and prediction

机器学习方法中所使用的卷积神经网络的结构如图3所示,通过建立12层深度卷积神经网络来学习三维粒子场。输入输出层尺寸均为64×64×32×1。最后一层的激活函数为Sigmoid函数,其他层为修正线性单元(Re LU)函数。除输入层和输出层外,其余层的尺寸均为64×64×32×16,并均采用批量归一化法[27]。输入层的卷积核大小为3×3×3×1,其他层的卷积核大小为3×3×3×16。

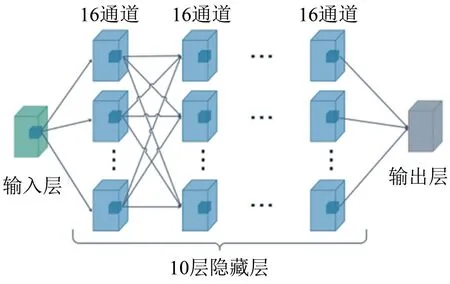
图3 神经网络结构示意图Fig.3 Schematic diagram of neural network structure

在实验中,通常无法通过测量获得粒子的精确位置和强度分布。因此,采用合成粒子场作为训练和测试数据。合成粒子场及其图像的生成使用了PR算法测试中常用的典型方法,详见王洪平[14]和叶志坚[16]等的研究。主要根据给定的映射函数计算粒子场的4个投影,模拟摄像机成像。然后计算初始MLOS字段,并将其作为上述3D-CNN的输入。

为了提高卷积神经网络的鲁棒性,我们在用于训练的20%的粒子图像中加入了高斯噪声。并在4幅粒子图像中加入不同程度的高斯噪声。按照添加噪声的典型方法[14,19],图像噪声的标准差σ用PR测试的nσ值来计算,其中噪声强度n的取值区间为0～0．20,间隔为0．05。实验结果表明:当训练样本数大于500时,新算法具有足够的稳定性和精确度。训练网络的损失函数定义为:

式中:F是真值目标矩阵,Fnn是网络输出矩阵,皆表示粒子空间灰度的矩阵;ε是一个小值,以防止分母为零,文章中ε取10－3;运算符“·”表示矩阵的内积,即矩阵中对应元素的乘积;sum()表示矩阵所有元素的灰度值总和;i是训练样本的索引序号;M是训练样本的数目。

3 结果与讨论

由于粒子重构技术很难用真实的实验数据直接进行验证测试,为了得到准确的比对结果,使用人工合成数据对AI-PR算法进行了验证测试。用与生成训练集相同的方式生成780×780×140测试粒子场。粒子播种密度ppp取值为0．05～0．30,间隔为0．05。噪声强度n取值为0．05～0．30,间隔为0．05。使用3种传统的PR方法:MLOS、MART-5次迭代和MART-10次迭代的方法,与本文提出的机器学习方法进行了比较。所有的训练和测试都是在Python编程的Tenserflow TMV1．13．1(Abadi等)[28]框架下进行的(www．python．org),并且使用到了Matlab编程软件(Math Works公司)。使用的计算机是一台Intel x99工作站,包含一个CPU为E5-2696 V4,64GB DDR4内存和一个RTX2080ti图形处理单元。

图4提供了ppp＝0．15的重构粒子场的中心截面图。很明显,MLOS只给出了一个非常粗略的粒子位置和强度分布的初始猜测,而AI-PR和MART可以更好的重构粒子场。进一步比较AI-PR和MART方法,可以发现MART比AI-PR产生更多的虚假粒子,并且强度分布更差。如果仔细观察粒子形状,可以发现MART重构的粒子具有更多的椭球形状,而AI-PR则可以更好地恢复成球形形状。

图4 粒子场截面图Fig.4 Cross-sections of particle field

如图5所示,在重构质量方面,AI-PR方法要优于MART方法。用质量因子Q来评价新技术的准确性和稳定性,即合成场与重构场之间的相关系数。图5(a)为无成像噪声情况下测得所有方法质量因子Q随粒子播种密度的变化。结果表明,AI-PR可以有效地从MLOS场中恢复粒子。它比MART方法有更好的Q值。当粒子播种密度为0．25时,AI-PR的Q值保持在0．7左右,而MART-10次迭代则降至0．6以下。在图5(b)粒子播种密度为0．15的样本中加入了噪声的影响,从图中可以发现对于所有方法,Q随着噪声强度的增加而减小,但是AI-PR对偏差的稳定性最好。

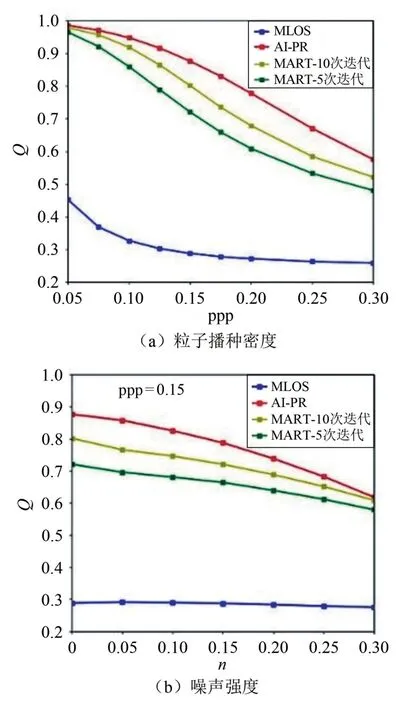
图5 几种方法的质量因子Q变化图Fig.5 Variation of quality factor Q of several methods

就计算效率而言,MLOS、MART-5次迭代、MART-10次迭代和AI-PR算法的计算时间分别为512．5、5333．5、9881．5和524．5 s。由 于AI-PR处 理包含了MLOS和CNN的计算时间,实际计算时间仅为12 s左右,但值得注意的是,前期卷积神经网络的训练耗时约为16 h,并且在测试中MART算法并未使用GPU加速。

除了评估新方法统计的品质因子之外,还针对粒子重构中经常出现的虚假粒子(Ghost particle)问题进行了测试。虽然虚假粒子也会在AI-PR中出现,其出现概率会随着粒子浓度增加而增大,但是其出现率非常低,以至于影响粒子重构质量因子的主要原因是灰度值分布的偏差。因为本文方法是以MLOS方法的初始场作为输入进行粒子场重构优化,其对粒子场是一个非常初步的猜测,只是为了实现粒子空间稀疏性的猜测,而最终粒子都将分布在MLOS初始场的灰度非零体素上,几乎不会出现粒子丢失现象。而机器学习有别于传统Tomo-PIV标定获得固定的映射函数,其能通过大量样本实现未知映射约束关系的学习,因此其求解稀疏欠定问题的能力更强,甚至可以求解1或0范数的优化问题。基于这些原因,机器学习能很好地避免虚假粒子的出现,尤其是在大样本训练集的前提下。

此外,有一点值得注意的是:目前测试数据为人工合成数据。最理想的方法是通过真实实验来验证重构结果,但由于在真实实验中难以得到真实粒子空间分布的信息,所以难以通过实验来进行算法验证。另一方面,粒子重构质量对流场统计特性的影响效果过于复杂且未知,很难评估具体哪个环节造成误差,因此也没有采用通过类似湍流边界层统计特性的评估来验证粒子重构算法。新方法在真实实验中的应用效果将在后续探索中进一步深化。

4 结 论

总的来说,基于机器学习方法的三维粒子重构技术在重构质量方面优于传统的基于MART的算法。

1)AI-PR技术相较于基于MART的传统算法,可以进一步剔除虚假粒子,并从二维粒子图像中有效的恢复粒子位置和形状,得到更加准确的粒子场分布。

2)AI-PR技术相较于基于MART的传统算法,具有更高的运算处理效率。

基于AI-PR技术的优势,该技术很有希望应用于更真实的实验。同时需要注意的是,对于不同的成像映射函数的实验,AI-PR需要在整个训练过程中来学习投影规则。今后的研究可以集中在体PIV的标定与AI-PR训练相结合,或者直接从AI-PR中进行粒子重构,而不需要标定以及针对不同实验情况来进行附加网络训练。