具有“前进-前进”运动模式的惯性压电驱动器

胡意立，胡 影，李建平，温建明，兰 虎

（浙江师范大学 浙江省城市轨道交通智能运维技术与装备重点实验室，浙江 金华321004）

1 引 言

压电精密驱动器由于体积小、输出精度高、反应速度快、抗电磁干扰强等显著优势［1］，受到科研人员的密切关注，并已成功应用于超精密制造［2］、生物医学［3］、光学仪器［4］等微操作领域。它们根据不同的驱动原理一般可以分为四类：超声驱动型［5］、直接驱动型［6］、惯性驱动型［7］和尺蠖驱动型［8］。惯性压电驱动器作为压电驱动器的一个大类，具有结构简单、分辨率高等优点［9-10］，满足细胞操作过程对驱动器集成化、定位精度的高要求，因此惯性压电驱动器在细胞操作等微操作领域具有很大的应用潜能。

然而，目前国内外研究人员所提出的惯性压电驱动器由于其在工作原理上存在的缺陷，都普遍存在着回退现象［11-12］。程光明等人以惯性压电旋转驱动器为研究对象，对比研究了非对称式惯性压电旋转驱动器和变摩擦力式惯性压电旋转驱动器的运动特性，试验表明非对称式与变摩擦力式压电驱动器的回退率分别为73.19%，65.67%［13］。Dalius Mazeika等人提出了一种基于矩形双晶片弯曲振动的惯性冲击式压电驱动器，驱动器输出力为0.21 N，最大输出速度达到40.376 mm/s，但是实验结果仍然存在回退现象［14］。传统惯性压电驱动器广泛存在的回退现象会直接影响其在运行过程中的定位精度和稳定性，从而严重限制了此类驱动器在精密操作领域的发展。近年来，研究人员们针对回退问题提出一些方法，比如通过磁流变控制前进和回退过程中的摩擦力［15］，通过复杂的波形输入来优化控制信号［16］，或是设计复杂的机械结构改善驱动器输出性能［17］。但是这些解决方法在实际操作中都较为繁琐，难以达到预期效果，只能在一定程度上抑制回退运动。因此，为了促进惯性压电驱动器在微操作领域的进一步发展，迫切地需要一种简单的、能彻底解决回退问题的方法。

本文提出并设计了一种基于双压电振子反向连接的非对称惯性压电直线驱动器。该驱动器在保留传统惯性压电驱动器结构简单、分辨率高等优点的基础上，通过“反接”接线方式，使驱动器工作在“前进-前进”的运动模式，从原理上彻底消除了此类驱动器一直以来存在的回退现象，并且在一定程度上提高驱动器的运动速度、稳定性以及能量转换效率，满足实际应用需求。所设计的惯性压电驱动器在细胞操作等精密操作领域具有良好的应用前景。

2 驱动器的结构设计

本研究所设计的新型惯性压电直线驱动器的结构如图1（a）所示。所设计的驱动器的总体大小为：70 mm×68 mm×39 mm（长×宽×高）。驱动器主要由一个承载盘，一个运动主体，一个底座，两对导轨，四片压电双晶片以及八对长、短夹持块组成。承载盘由四根尼龙柱固定在运动主体上，用于放置改变摩擦力的质量块以测试驱动器承载性能；八对长、短夹持块由螺栓固定在运动主体上，利用非对称夹持结构实现驱动器的直线运动。与悬臂梁结构相比，样机的设计中采用的两端固支梁结构具有结构紧凑、稳定性高等优点［18］。

如图1（b）所示为Guangming Cheng等人首次提出基于非对称夹持结构的新型惯性压电驱动器的驱动原理［19］：由于压电片向短夹持侧弯曲时的等效刚度小于向长夹持侧弯曲时的等效刚度，其通过弯曲振动对应产生的驱动力F1，F2方向相反，且F1＞F2。振子1，2与振子3，4采用分布完全相反的非对称夹持结构，通过将控制信号与这两对振子的交替连接，可以使驱动器具有双向运动的能力，如图1（c）所示。

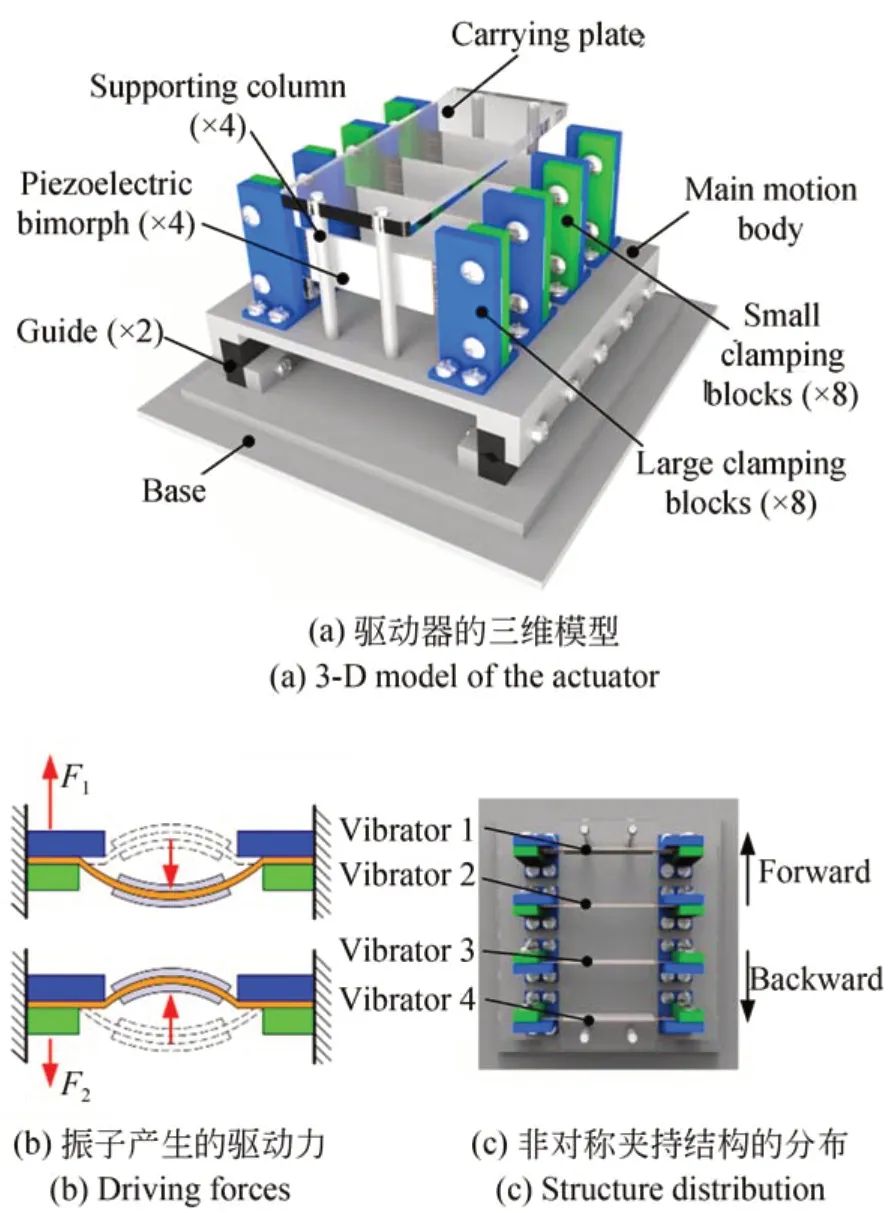
图1 惯性驱动器的总体结构Fig.1 Overallconfigurationoftheproposed inertialactuator

3 接线方式与运动原理

3.1 接线方式

传统惯性压电驱动器通常在控制信号与两个压电片之间采用完全相同的接线方式［20］，使两个振子处于相同的运动状态，本文将这种传统的接线方式命名为“正接”。图2所示为本文所提出的新型接线方式，振子1的压电晶片和金属基片分别与控制信号的正、负极相连，但是振子2采用的接线方式与振子1完全相反。由于双振子反向连接的特点，本文将这个新型的接线方式命名为“反接”。在反接条件下，当控制信号处于b→c阶段，振子1向短夹持侧弯曲，产生向左的相对较大的驱动力F1，振子2向长夹持侧弯曲，产生向右的相对较小的驱动力F2，驱动器在振子1和振子2的共同作用下受到向左的驱动合力∆F（∆F=F1-F2）；当控制信号处于d→e阶段，振子1向长夹持侧弯曲，产生向右的相对较小的驱动力F2，振子2向短夹持侧弯曲，产生向左的相对较大的驱动力F1，因此在过程Ⅱ，驱动器同样受到向左的驱动合力∆F。

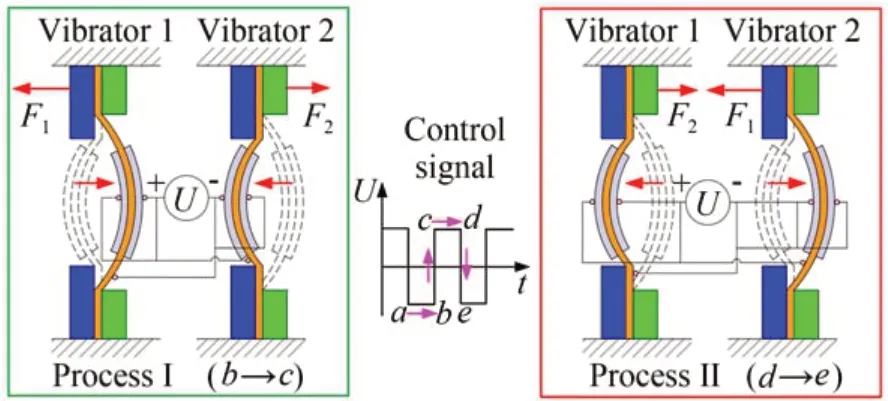
图2 反接接线方式示意图Fig.2 Schematic diagram of the converse wiring method

3.2 运动原理

在传统的正接的接线方式下，驱动器在前半个周期前进一大步，在后半个周期回退一小步，本文将这种运动模式命名为“前进-回退”运动模式。图3所示为反接条件下驱动器的运动原理图，以振子1和振子2与控制信号相连接为例进行阐述。过程Ⅰ，控制信号处于b→c阶段，振子1向长夹持侧弯曲，产生向后的驱动力F2，振子1向长夹持侧弯曲，产生向后的驱动力F2，驱动器在向前的驱动合力∆F（∆F=F1-F2）的作用下从P1运动到P2，前进位移S1；过程Ⅱ，控制信号处于d→e阶段，振子1向短夹持侧弯曲而振子2向长夹持侧弯曲，同样产生向前的合力∆F，使驱动器从P2运 动 到P3，前 进 位 移S2（S2=S1）。综 上 所述，驱动器在一个周期内前进两步，总位移为∆S（∆S=S1+S2=2S1）。根据驱动器在反接条件下的运动特点，将此运动模式定义为“前进-前进”运动模式。在周期性的信号激励下，驱动器将重复上述步骤，实现定向前进运动。

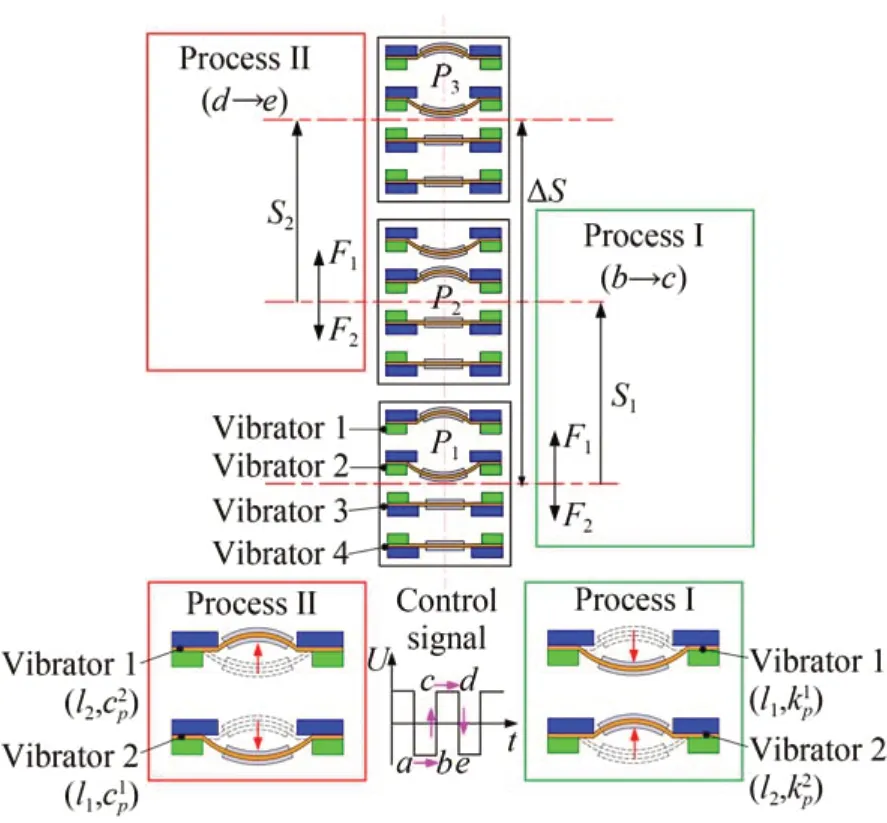
图3 “前进-前进”运动模式的运动原理Fig.3 Operation principle with the“forward-forward”motion mode

基于非对称夹持的驱动原理，一对振子可以实现驱动器在单方向上的大行程运动。因此，利用分布完全相反的两对振子的交替使用来实现驱动器的双向运动。将振子3和振子4与控制信号相连，就能实现反向的单周期双步的直线运动。

4 驱动主体理论分析

为了更好地分析驱动器在“前进-前进”运动模式下的运动特性，在该模式运动原理的基础上建立了机构的动力学模型如图4所示，并进行了Matlab/Simulink仿真分析。根据图3所示的“前进-前进”运动模式的运动原理，振子1和振子2的运动状态不同。根据图4所示的动力学模型，在动态电场作用下两端固支的振子1的动力学方程可表示为：

图4 “前进-前进”运动模式的动力学模型Fig.4 Dynamic model with“forward-forward”motion mode

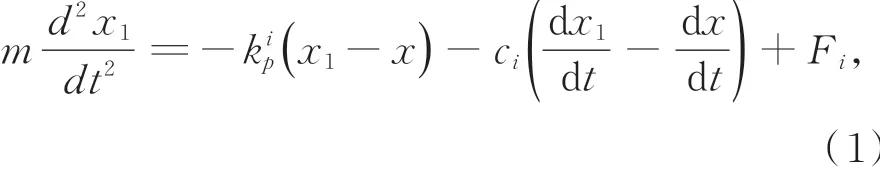
其中：m表示振子的质量，x1，x分别表示振子1和驱动器主体相对地面的位移分别表示振子1的等效刚度系数和阻尼系数，F i表示振子1弯曲产生的驱动力。

振子2的动力学方程可表示为：

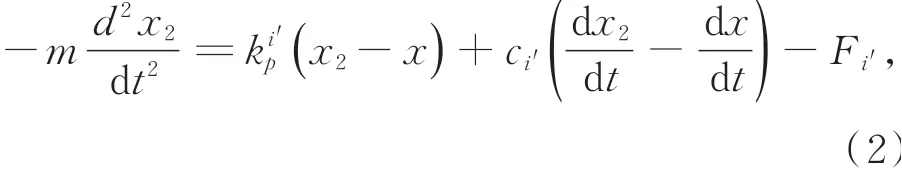
其中：x2表示振子2相对地面的位移分别表示振子2的等效刚度系数和阻尼系数，F i'表示振子2弯曲产生的驱动力。在过程Ⅰ，i=1，i'=2；过程Ⅱ，i=2，i'=1。

驱动器运动主体的动力学方程可表示为：

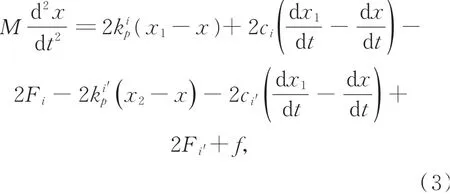
其中：M表示驱动器运动主体的质量，f是一个矢量，表示运动主体受到的摩擦力的大小和方向。根据物体运动特性，摩擦方向始终与速度方向相反。因此，利用符号函数确保摩擦力与速度方向相反：

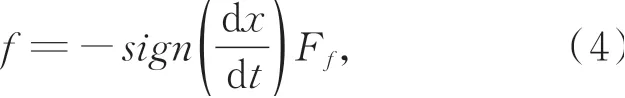
其中：F f是一个标量，只表示主体受到的摩擦力的大小。

将式（4）代入式（3），可以得到驱动器运动主体的完整的动力学方程：

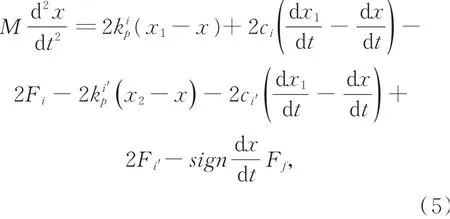
由于Lugre摩擦模型是静态摩擦与动态摩擦相结合的综合摩擦模型［21］，能够较为准确地描述驱动器运动过程中产生的摩擦力，所以采用Lugre摩擦模型进行仿真分析。导轨之间的摩擦可以表示为［22］：

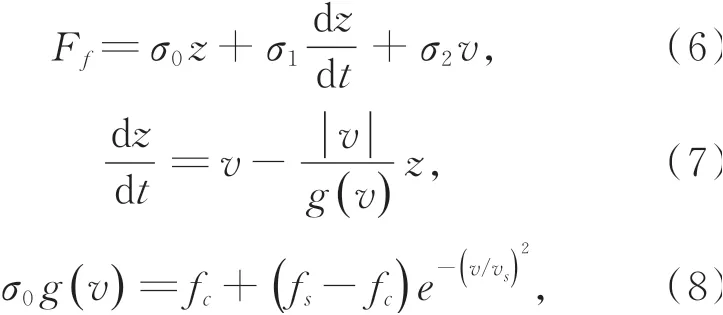
其中：σ0表示鬃毛的刚度系数，σ1为阻尼系数，σ2为黏性摩擦相对速度系数，z代表鬃毛的平均变形，v表示两个接触表面的相对速度，fc，fs分别表示库仑摩擦等级和黏性摩擦等级，vs表示Stribeck速度，g(v)是描述Stribeck效应的函数。

5 驱动器的性能试验测试

5.1 接线方式

为了测试所设计的压电惯性驱动器样机的输出性能，在图5所示的试验测试系统中进行了一系列试验，样机的主要元件的结构尺寸如表1所示。信号发生器产生的方波信号被功率放大器放大后作用到驱动器上。激光测位仪测量驱动器的位移并将数据结果输出到计算机上，通过计算机进行数据记录和处理。此外，功率分析仪用于测量驱动器的功耗。

图5 压电驱动器试验测试系统Fig.5 Experimental system of prototype

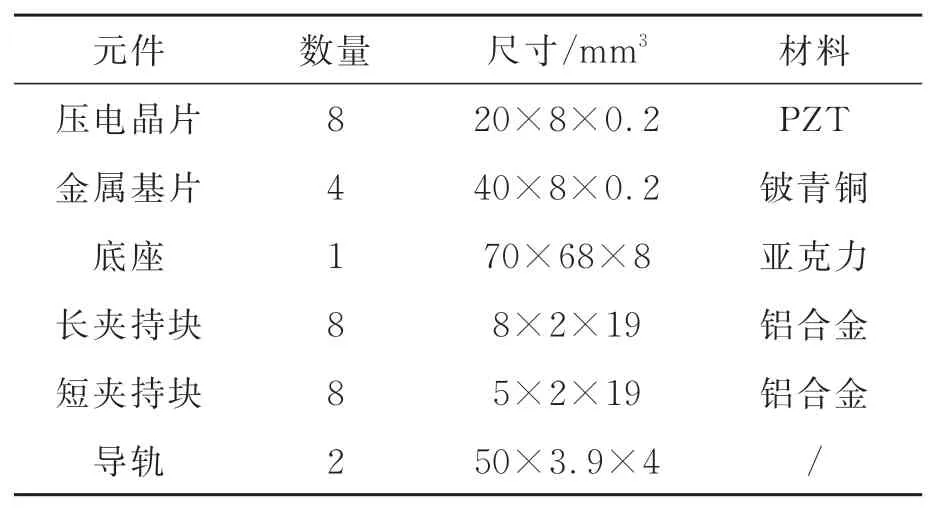
表1 驱动器主要元件的材料及尺寸Tab.1 Material and size of main components of actuator

5.2 驱动器步距特性测试

图6 （a）所示为驱动器在不同电压以及1 Hz频率的试验条件下，两种不同的运动模式的步距特性图。在传统的“前进-回退”运动模式下，驱动器在30，50和70 V电压时的平均单周期步距分别为2.16，4.14和6.08μm；在所提出的“前进-前进”运动模式下，驱动器在30，50和70 V电压时的平均单周期步距分别3.08，5.46和7.88μm。由试验结果可得，相同的控制信号条件下，“前进-前进”运动模式可以使驱动器可以达到相对较大的运动速度。从实验结果可以看出工作在“前进-前进”运动模式下的驱动器在实验条件范围内的回退率都达到0%，消除了传统运动模式下惯性压电驱动器存在的回退运动。

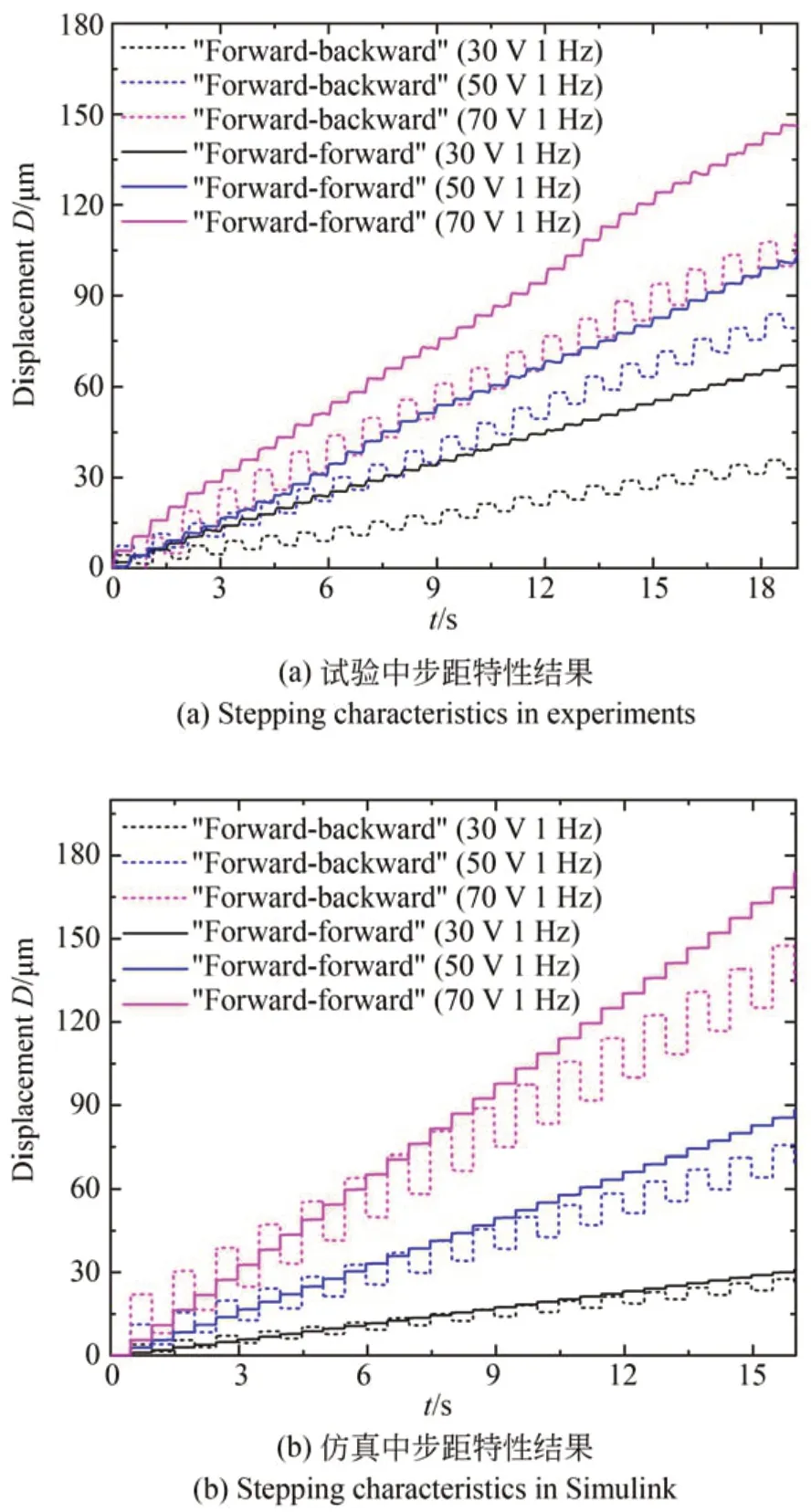
图6 步距特性对比Fig.6 Comparison of stepping characteristics

图6 （b）所示为试验对应的电压和频率条件下得到的步距特性仿真结果。从图中可以看出，在相同的激励信号下，“前进-前进”运动模式的平均速度明显大于“前进-回退”运动模式，这与试验得到的结果相吻合，证实了试验结果的准确性。

5.3 驱动器功耗特性测试

两种运动模式下驱动器的功耗与能量装换效率如图7所示。能量转换效率通过下式计算：

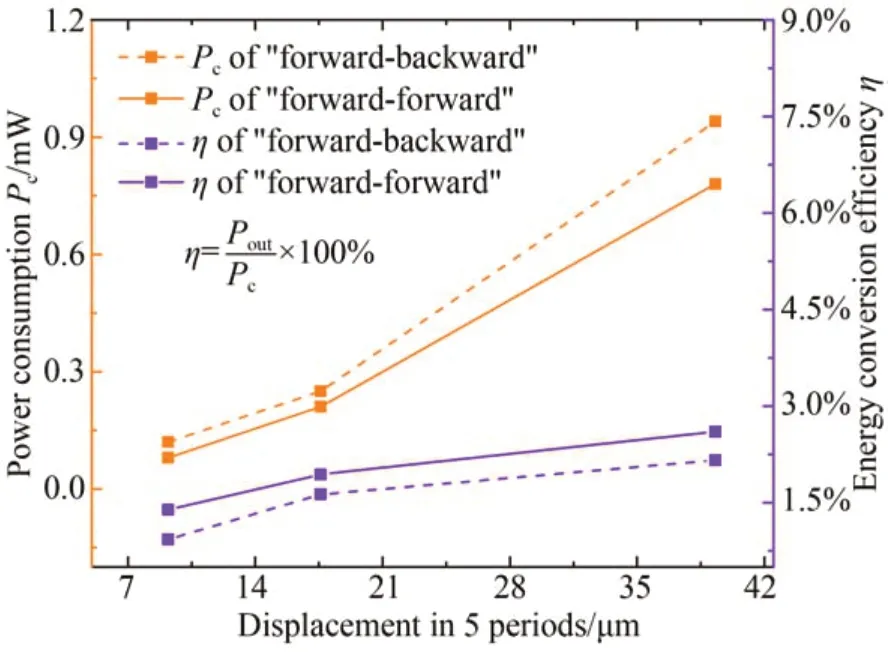
图7 功耗特性对比Fig.7 Comparison of power consumptions

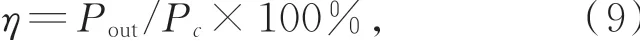
其中：Pout表示输出功率，Pc表示消耗功率，即功耗。在“前进-回退”运动模式下，驱动器在5个周期前进9.20，17.60和39.30μm消耗的功率分别为0.12，0.25和0.94 mW，能量转换效率分别为0.93%，1.63%和2.16%。在“前进-前进”运动模式下，驱动器在5个周期前进9.20，17.60和39.30μm消耗的功率分别为0.08，0.21和0.78 mW，能量转换效率分别为1.39%，1.94%和2.60%。显然，驱动器在“前进-前进”运动模式下达到相同速度时消耗的功率低于“前进-回退”运动模式，并且其能量转换效率高于“前进-回退”运动模式。

5.4 驱动器稳定性测试

图8 （a）、（b）所示分别为驱动器在“前进-回退”运动模式和“前进-前进”运动模式下的重复性试验结果。最大偏差和标准差计算方式为：

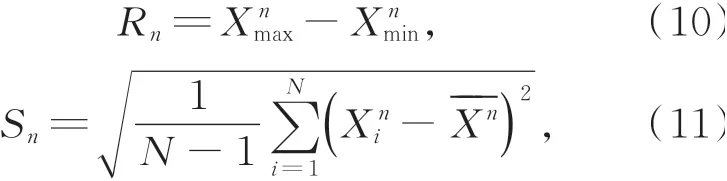
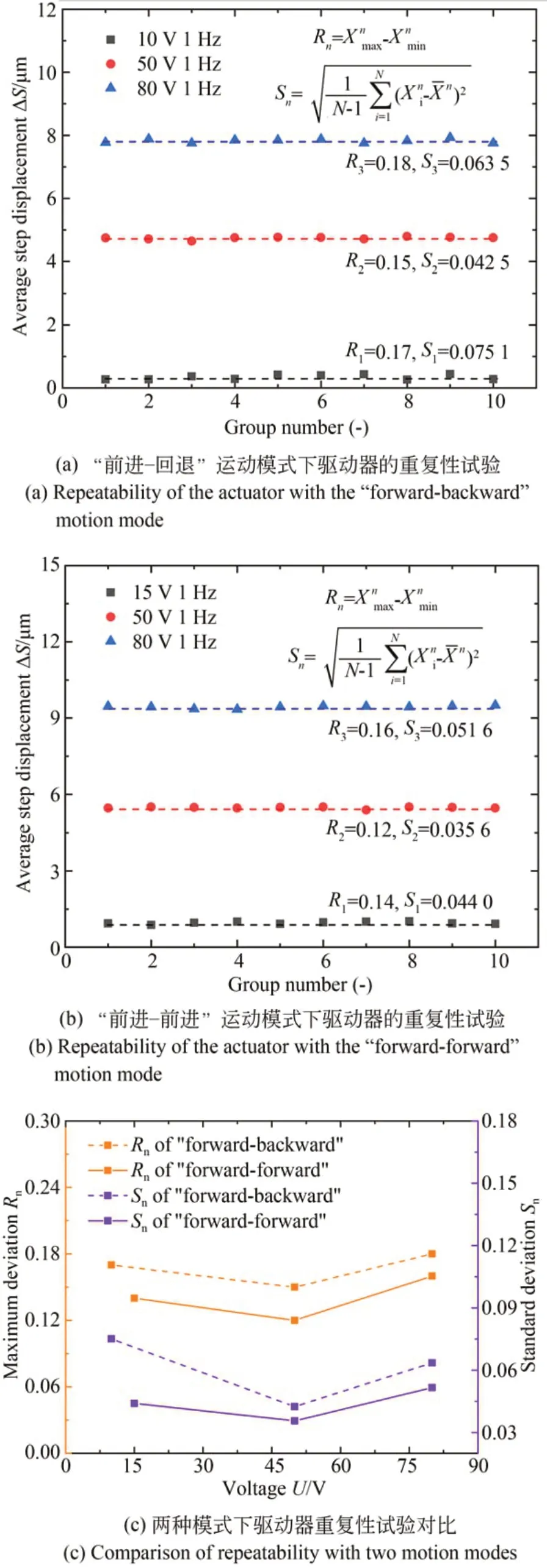
图8 稳定性对比Fig.8 Comparison of repeatability

5.5 驱动器双向运动性能测试

通过交替使用夹持方式分布相反的两对振子，可以使驱动器获得双向运动的能力。图9所示为驱动器在“前进-前进”运动模式下双向运动试验结果。驱动器在10个周期内双向运动位移的累计误差率可以通过公式（12）计算：

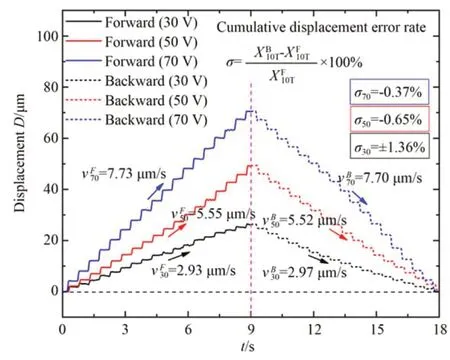
图9 驱动器双向运动试验Fig.9 Experiment on bidirectional motion of actuator

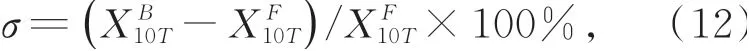
正向运动和反向运动的累计位移。通过上式计算可得，驱动器在30，50和80 V时的累计误差率分别为+1.36%，-0.65%和-0.37%。由于在不同电压条件下的累计误差率都很小，表明驱动器在“前进-前进”的运动模式下具有稳定、可控的双向运动能力。

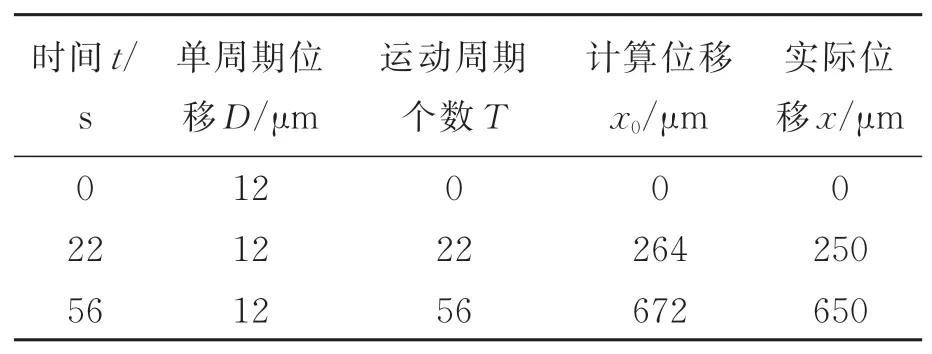
表2 驱动器在100 V和1 Hz条件下细胞药物注射模拟实验结果Tab.2 Simulation experiment results of cell drug injec⁃tion with actuator at 100 V and 1 Hz

5.6 细胞药物注射模拟实验

为了测试所设计的驱动器在细胞操作领域的应用潜能，将玻璃微针固定在样机上，对斑马鱼胚胎进行了药物注射模拟实验。实验测得在100 V电压和1 Hz频率的控制信号作用下驱动器的平均单周期位移约为12μm，经过22 s和56 s后驱动器通过计算可求得前进的位移分别为264μm和672μm，在细胞药物注射模拟实验中实际前进的位移约为250μm和650μm。图10显示玻璃微针在驱动器的带动下不断靠近斑马鱼胚胎，并在经过56 s后成功刺入胚胎。实验结果表明该驱动器适用于细胞药物注射研究，进一步证实了该驱动器在细胞操作领域的应用价值。

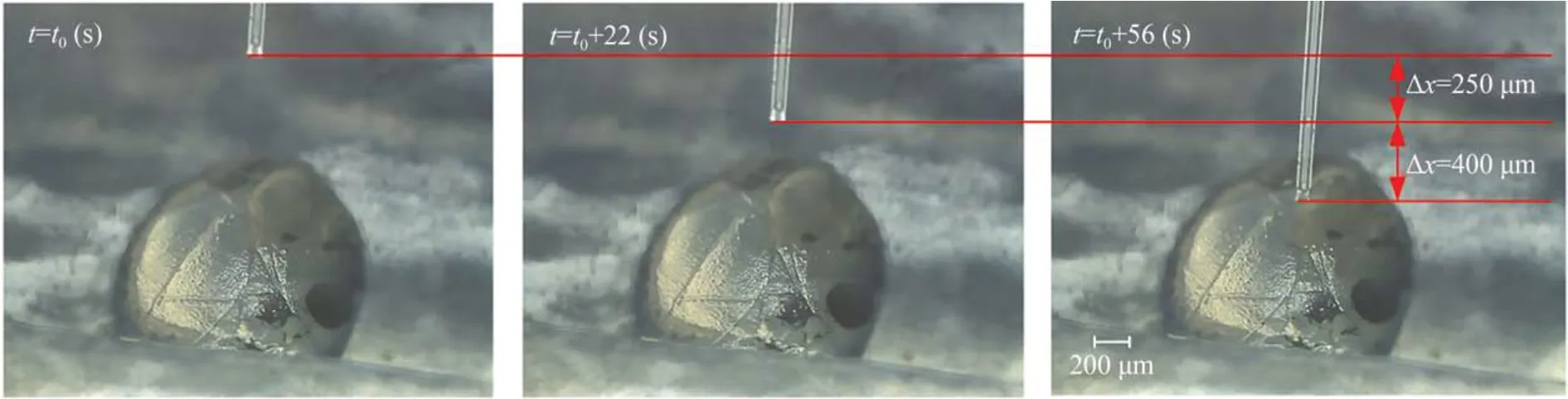
图10 细胞药物注射模拟实验Fig.10 Simulation experiment of cell drug injection

6 结 论

本次研究提出了一种基于双振子反向连接的惯性压电驱动器，试验结果表明，反接条件下驱动器可以实现单周期“前进-前进”的运动模式。与传统的惯性驱动器相比，运行在该模式下的驱动器具有以下四大优点：第一，驱动器在任何试验条件下都实现无回退；第二，在一定程度上提高了驱动器的能量转换效率，实验结果显示能量转换效率从2.16%提高至2.60%；第三，使驱动器获得相对较大的运动速度，驱动器速度从6.08μm/s增大至7.88μm/s；第四，该模式具有相对更优的重复性和稳定性，最大偏差为0.12μm，标准偏差为0.035 6。总的来说，基于所提出的反接接线方式，驱动器彻底解决传统惯性压电驱动器一直存在的回退问题，提高了驱动器的运动速度、能量转换效率以及稳定性，并且具有双向运动能力。细胞药物注射模拟实验结果表明，所设计的驱动器在细胞操作等微操作领域具有极大的应用潜能。