永磁球形电机转子区间划分及辨识策略研究

李洪凤，柏恩潮，陈旭，李斌

(1.天津大学 电气自动化与信息工程学院，天津 300072；2. 北京四方继保自动化股份有限公司，北京 100085)

0 引 言

随着现代科技的发展，对体积小、重量轻、精确度高、可靠性强的多自由度运动装置的需求越来越迫切。当前的多自由度运动，需要多台电机配合复杂的机械传动结构级联才能实现。球形电机可以单轴实现多自由度运动，从而可以大大简化整个系统的机械结构，有望促使多自由度运动系统向小型化、微型化发展[1-2]。

转子的位置信息对于永磁球形电机多自由度的精准控制非常重要，它决定了电机现在的状态，以及下一步的控制策略。然而球形电机的多自由度运动需要获取转子位置的三维信息，传统旋转电机的位置检测方案无法简单移植，因而众多学者开展了球形电机的位置辨识研究。目前的球形电机转子位置辨识还处于理论研究阶段。笔者从可以查到的文献中，归纳出球形电机转子的位置辨识主要分为两种方向，一种是不依赖于磁场模型的转子位置辨识方案，另一种是基于磁场模型的转子位置辨识方案。不依赖于磁场模型的转子位置辨识方案通常是需要在转子外部安装附加设备来检测转子的位置。文献[3-4]提出了一种基于滑轨支架的转子位置辨识方案，通过在滑轨以及输出轴上安装旋转编码器来得到转子的位置信息。文献[5-9]提出了一种基于视觉的转子位置辨识方案，该方案需要首先对转子表面进行图案预处理，然后通过外置视觉传感器来采集转子连续的图像，通过对图像的辨识计算出转子的位置。文献[10]提出了一种利用微机电系统姿态传感器进行球形电机转子位置辨识的方案，通过对微机电系统姿态传感器内部的陀螺仪以及三轴加速度计的输出进行处理，计算出球形电机的转子位置。以上文献提出的转子位置辨识策略都不需要建立转子磁场的模型，只需要根据在球形电机外部安装的传感器的输出数据就可以计算出转子的位置，计算量较大。文献[11-12]提出了一种基于三维霍尔传感器的永磁球形电机转子位置辨识方案，通过解算三维霍尔元件测量出的磁场信息与转子位置之间的关系，得到了转子的位置信息。文献[13]提出了一种利用三维霍尔传感器来测量球形轮式电机的转子位置的方案，通过建立误差函数，利用神经网络算法计算出了转子的旋转角度。文献[14]提出一种基于线性霍尔传感器的转子位置辨识方案。将4个霍尔传感器组成一个单元，利用传感器单元与磁场等高线几何相交位置求解出传感器单元与磁极间的位置差，进而辨识出转子的位置。文献[15]安装了64个线性霍尔传感器来辨识转子位置，通过分析线性霍尔传感器的检测值与磁极之间的距离，计算出磁极的位置，进而辨识出转子位置。

综上，不依赖于磁场模型的转子位置辨识方案一般都需要在球形电机的外部额外安装传感器辅助设备，从而造成转子位置辨识系统体积庞大，不利于球形电机向小型化、微型化方向发展。基于滑轨支架的转子位置辨识属于接触型转子位置辨识，滑轨支架带来的摩擦问题制约了该辨识方案的发展。基于视觉的转子位置辨识系统需要处理的数据量较大，因而对检测系统的处理器性能要求较高，造价较高。基于霍尔传感器的转子位置辨识方案，传感器体积小，可以内嵌在球形电机定子内表面，而且对处理器的性能要求不高。但是目前的基于霍尔传感器的转子辨识方案均是基于磁场的解析模型。

本文提出的基于霍尔传感器阵列的球形电机转子位置辨识方案基于有限元仿真结果来设定传感器的阈值和安装位置，不依赖于磁场的解析模型。根据有限元仿真得到的磁场分布特点设定线性霍尔传感器转换编码的阈值，由24位编码和极性编码两种编码来共同确定转子磁极位置。

1 电机的基本结构及工作原理

永磁球形电动机的结构如图1所示，由转子和定子两大部分组成，转子带有输出轴，在转子赤道上以N-S-N-S的交替顺序均匀排列着4个柱形磁极，磁极半径15 mm，厚度5 mm，材料为NdFeB35，定子壳内半径为44 mm，外半径49 mm，以赤道线为对称分布上下两层定子线圈。通过控制上下两层定子线圈电流可以使转子实现滚转、俯仰和偏航运动。

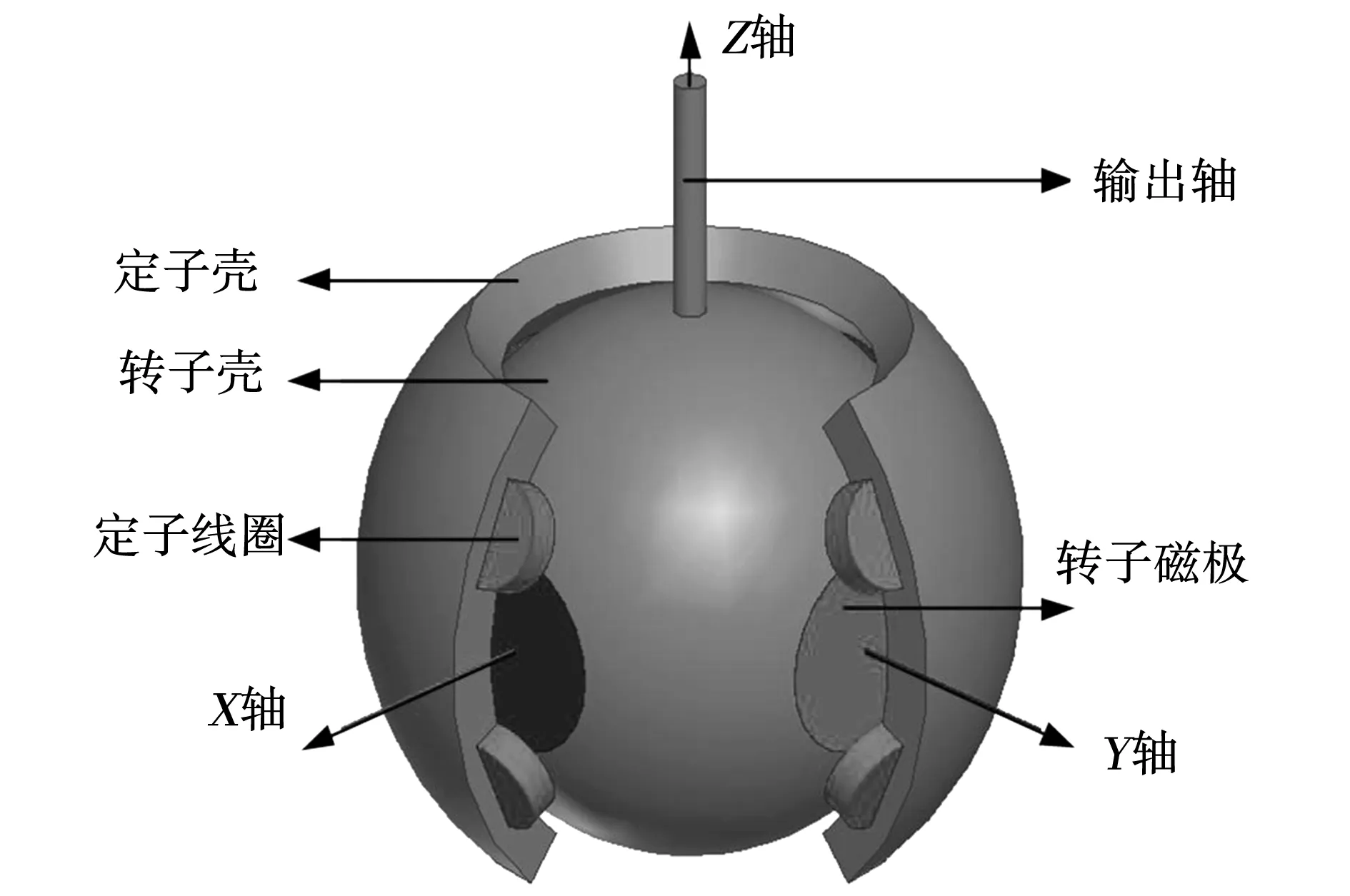
图1 永磁球形电机结构Fig.1 Structure of the permanent magnet spherical motor

建立转子有限元模型，如图2(a)所示。网格线位于距离转子球外表面4 mm的定子内表面上。网格线的划分分为经度方向以及维度方向。经度方向上，纬度角θ每间隔5°取一条纬度线，维度方向上，经度φ每隔1°取一个点，总共得到360×35个。仿真出转子表面的径向磁感应强度如图2(b)所示。

由图2(b)可以得出，在θ方向上，磁场值有一组波峰，跨度区间达到了50°。在φ方向上，磁场类似正弦分布，存在两个波峰，两个波谷。

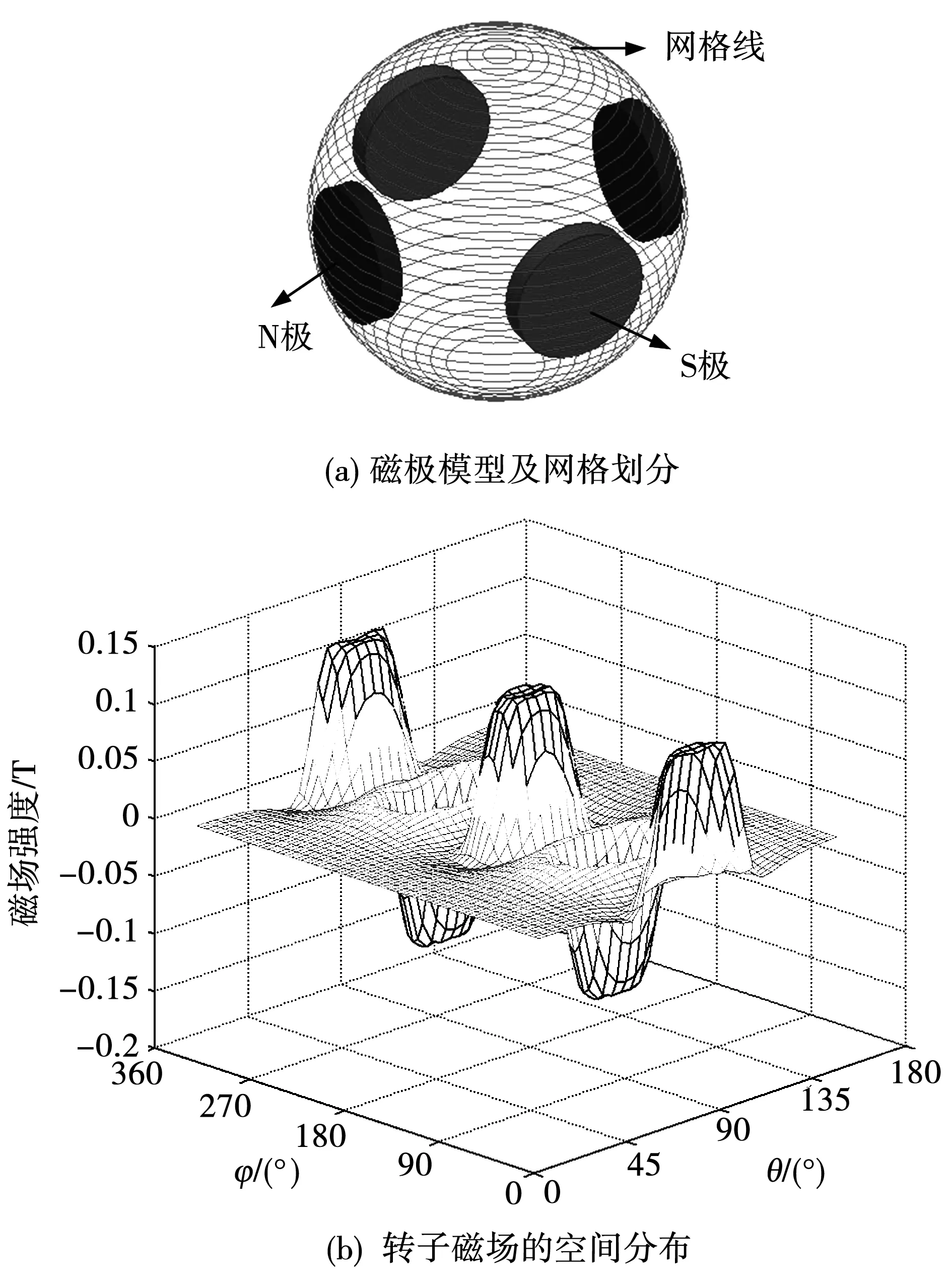
图2 ANSOFT模型、网格划分及磁场数据图Fig.2 Rotor model,mesh model and magneticfield data graph

2 阈值设计

阈值的设计需要考虑磁极、定子线圈的磁场的影响，以及实验中使用磁极实验值与有限元软件模拟值之间的误差。

2.1 转子磁极漏磁的影响

转子外半径40 mm，定子内半径44 mm。转子上的4个磁极在定子内表面上产生的磁场在零点附近不是单向光滑的，因为转子球壳不是导磁材料所以存在漏磁，如图3。

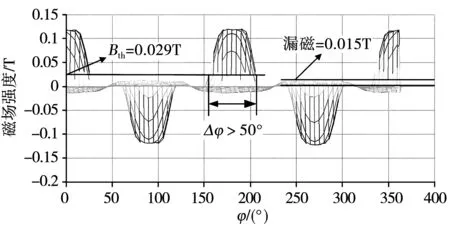
图3 在φ方向的磁场波动Fig.3 Fluctuating magnetic field in the direction of φ

由图3可以看出，漏磁的最大值在0.015T，为了消除漏磁对编码带来的影响，本文定义阈值B1，该阈值满足条件B1>0.015T。

2.2 定子线圈的磁场影响

在电机控制过程中，通电后的定子线圈产生的磁场会影响磁场检测。解决这一影响的方法是将阈值设定为大于定子线圈在传感器附近的磁场最大值。当一个定子线圈为200匝并通电1A得到其磁场分布图，取穿过定子线圈中心的一条线分析其周围的磁场变化，如图4。

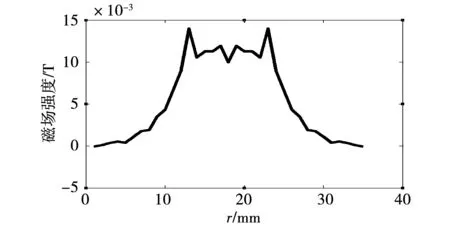
图4 线圈磁场随距离线圈中心的距离r的变化Fig.4 Coil magnetic field varies with the distance r from the coil center

由图4可以得出单个线圈中心的磁场最大值在0.012T左右。当多个定子线圈通电时，线圈产生的磁场最大值大于0.012T。为了便于消除由定子线圈磁场带来的影响，选取的阈值B2应根据具体通电策略确定的通电线圈确定。

综上，选取阈值为Bth=Max{B1，B2}。

2.3 实验值与FEA磁场仿真值的误差影响

由于FEA仿真软件得出的磁场与实验检测值之间也会存在一定的误差。因此，使用高斯计对磁极中心磁场进行了多次测量取平均值并与FEA得出的磁场进行对比，得出误差绝对值。定义转子的初始位置为X正半轴穿过N磁极中心，Y正半轴穿过S磁极中心。经过测量，可以得到有限元分析模拟值与实验测量值之间的绝对值误差最大值B3约为0.014T。

为了避免未被考虑的微小误差，在Bth=Max{B1，B2}的基础上叠加误差绝对值的最大值0.014T。当线性霍尔传感器输出的磁场值的绝对值大于Bth时，此时将该传感器的输出记为1，否则记为0。

3 传感器位置设计

根据传感器阈值对定子球内表面进行球面空间划分来确定传感器的放置位置。转子磁极产生的磁场大于阈值的位置在定子球壳内表面构成一个近似圆形区间，我们将该圆形区间命名为单元区间。在单元区间的中心放置一个传感器。

在赤道线上取8个点作为单元区间的中心点，单元区间在θ方向和φ方向上的跨度角为50°，在XOZ平面上的投影如图5所示。

图5 单元区间划分示意图Fig.5 Schematic diagram of cell regions division

在定子内表面赤道面均匀取8个单元区间中心点，构造8个相同的单元区间。将此8个单元中心点首先沿经度线上下移动22.5°，然后再沿着纬度线移动22.5°，得到上下两层各8个单元区间中心点。得到三层单元区间示意图如图6所示。

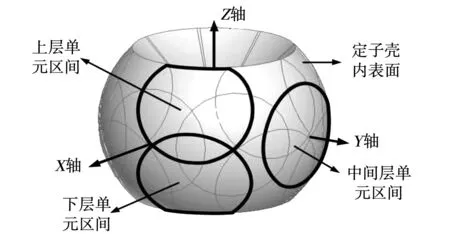
图6 单元区间示意图Fig.6 Cell regions diagram

由于转子的运动范围有一定限制，转子的滚转与俯仰范围在(-45°,45°)的范围，所以上层单元区间和下层单元区间并不完整。

传感器中心与单元区间几何中心重合。若磁极中心在某一单元区间之内，则该单元区间几何中心处的传感器必在该磁极的有效磁场的覆盖下，传感器输出编码信号必为1，如图7。

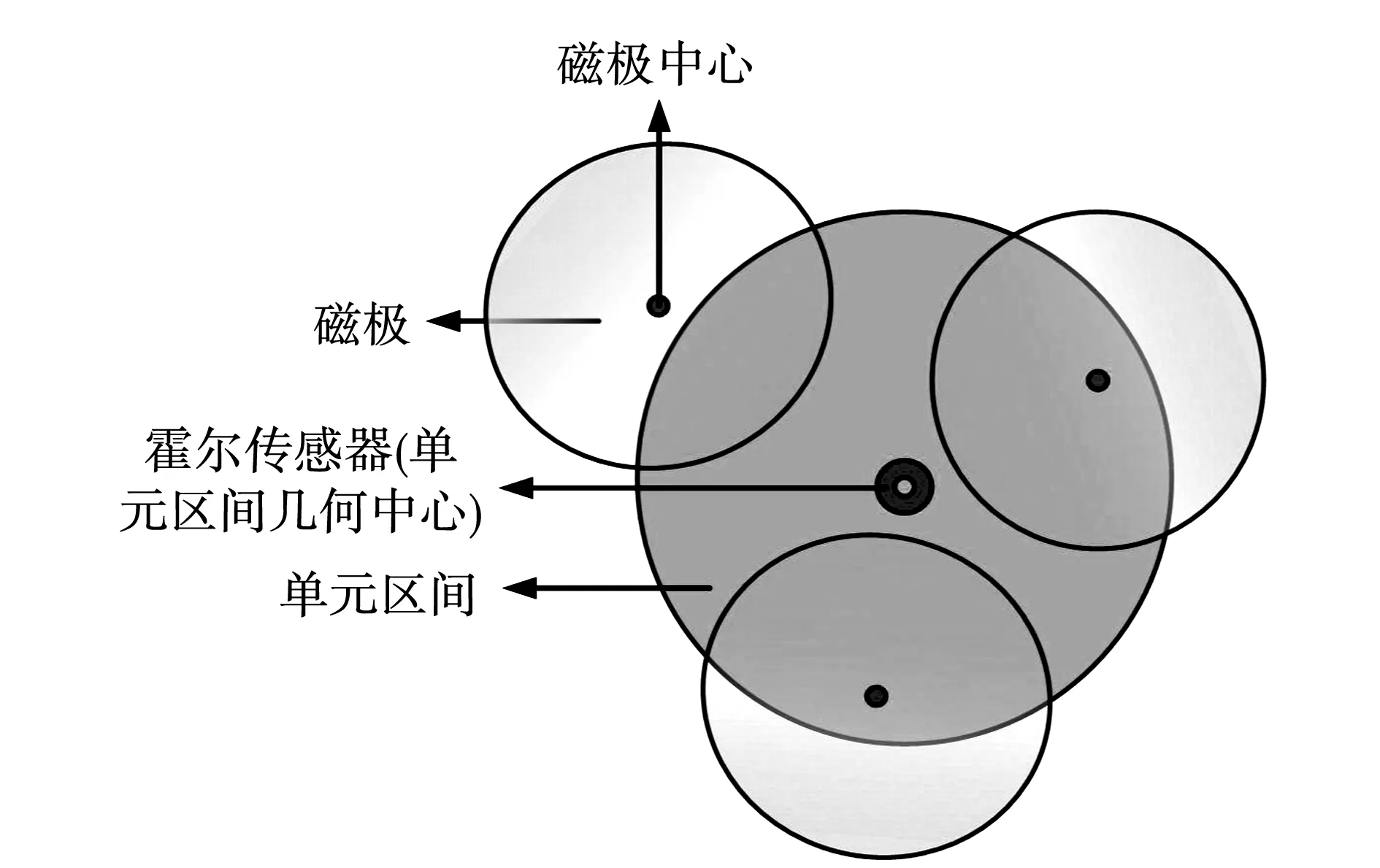
图7 磁极与单元区间的关系Fig.7 Relationship between the magnetic poles and the cell interval

在每一个单元区间的几何中心处均放置一个线性霍尔传感器，得到传感器放置方式如图8所示。在定子表面上一共分布了24个传感器，分为上中下三层，每层8个传感器，上中下三层编号开头分别为1、3、2。上层传感器编号分别为S1-1、S1-2、…、S1-8，下层传感器编号分别为S2-1、S2-2、…、S2-8，中层传感器编号分别为S3-1、S3-2、…、S3-8。传感器阵列编码由24个霍尔传感器的输出组成。

图8 传感器编号策略Fig.8 Sensor numbering strategy

对传感器阵列的编码规则如下：1)为了分辨磁极位置，将24个传感器输出的磁场值绝对值与磁场阈值比较后得到输出编码。称这种编码称为24位编码。2)为了辨别磁极的极性，将24个传感器中输出编码为1的传感器进行二次编码得到一组新的编码用来判断磁极极性。将输出编码为1的传感器的磁场测量值并与0进行比较，大于0编码为1，否则为0，这组编码称为极性编码。

4 转子位置辨识原理

单元区间在定子表面上相互重叠形成了范围更加小的区间。定义这些区间为位置区间。因为定子内表面的位置区间是关于球心对称的，因此只分析其中的代表性位置区间，其余区间分析方法与其分析方法相同。

选取的代表性位置区间包含P1-1、P1-2、…、P1-16。定子内表面由8组这样的16个位置区间组成，每一组的编号如图9(a)。16个位置区间的分析以及区间与传感器分布示意图如图9(b)。

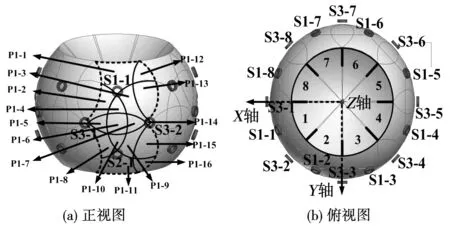
图9 位置区间的编号示意图Fig.9 Numbering diagram of the position interval

如图9所示，当磁极中心位于位置区间时的传感器阵列输出情况如表1所示。

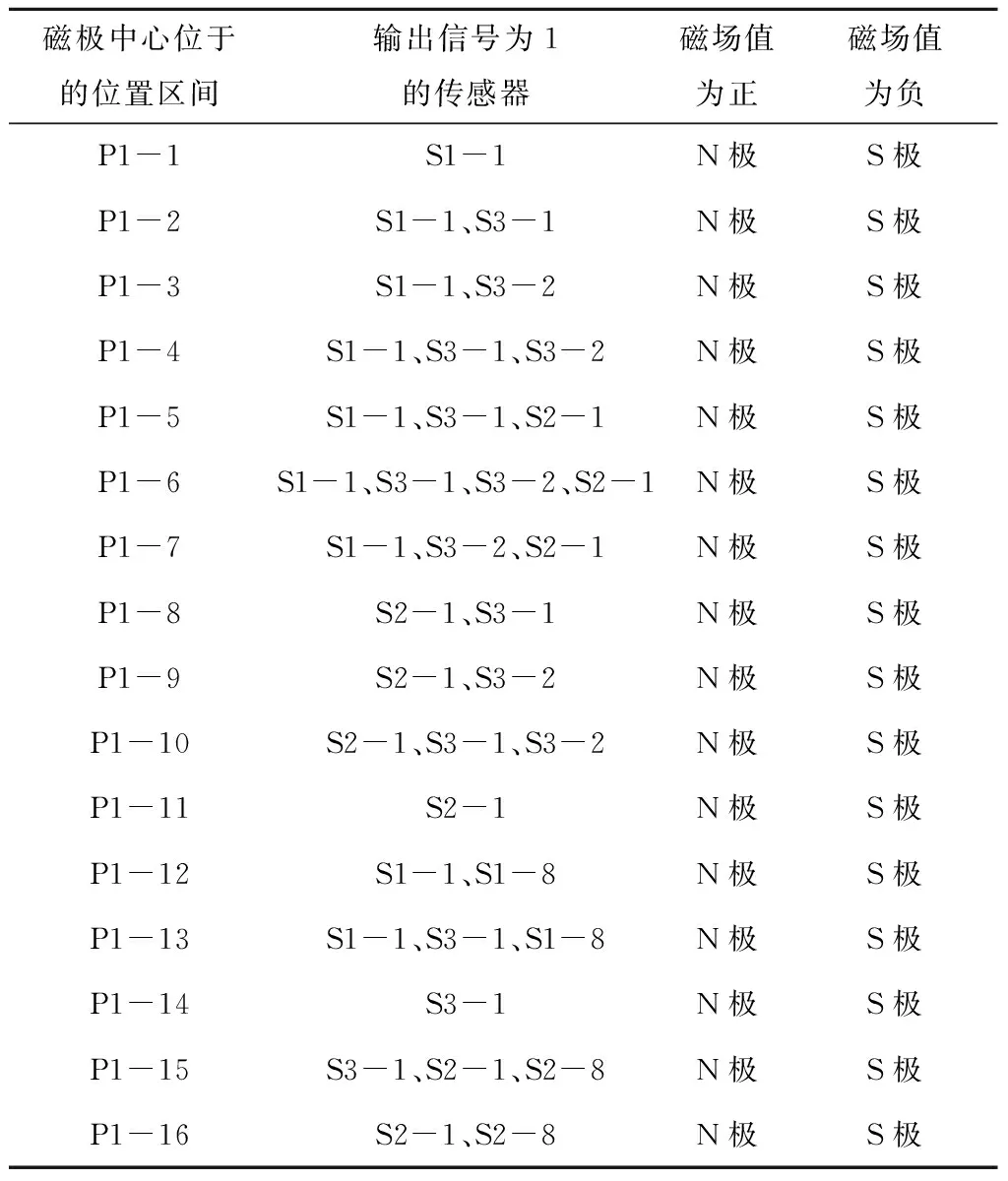
表1 传感器阵列输出与磁极位置

表1总结了转子磁极中心位于所有代表位置区间的情况。将24位编码与极性编码结合，并分析了当转子进行偏航运动，并且某一磁极位于位置区间P8-14、P1-5、P1-6、P1-7、P1-14、P2-5、P2-6、P2-7内时，传感器阵列输出的24位编码和极性编码，如表2。

表2 24位编码和极性编码

从表2可以发现，当S磁极位于P8-14和P4-14的位置区间，N磁极位于P2-14和P6-14的位置区间时，传感器S3-1、S3-3、S3-5、S3-7输出的信号均为1，可以得到的24位编码是0000/0000/0000/0000/1010/1010，极性编码为1010。

当转子在偏航运动基础上进行滚转和俯仰运动时，转子磁极中心会位于任意位置区间内，本文选取几个代表性区间进行24位编码和极性编码分析，如表3所示。

表3 24位编码和极性编码

当N磁极的中心位于P1-1和P5-11的位置区间，S极的中心位于P3-6、P7-6的位置区间时，传感器S3-1、S3-3、S3-7、S2-3、S2-5、S2-7、S3-4、S3-4、S3-7、S3-8输出的信号均为1，我们可以得到的24位编码是1010/0010/0010/1010/0011/0011,极性编码是1000/1000/00。

根据表2和表3中磁极位置与传感器阵列输出的编码信息，得出24位编码可以判断出转子4个磁极所在的位置区间，极性编码可以判断出磁极极性，将二者结合就得出了转子的位置。以两个例子对转子位置辨识的基本原理进行详细分析。

1)当N磁极中心位于位置区间P1-1、P5-11，S磁极中心位于位置区间P3-6、P7-6，此时传感器阵列24编码为1010/0010/0010/1010/0011/0011。将24位编码排布成如下形式，如图10。

图10 编号信号与传感器之间的关系Fig.10 Relationship between number signal and sensor

由图10可以得出传感器S1-1、S1-3、S1-7、S2-3、S2-5、S2-7、S3-3、S3-4、S3-7和S3-8输出信号为1，其中S1-3、S2-3、S3-3和S3-4相邻组成了四边形，在位置区间P3-6中必有一个磁极；其中S1-7、S2-7、S3-7和S3-8也组成了四边形，在位置区间P7-6中必有一个磁极。传感器S1-1输出编码为1，且与其相邻传感器输出为0，因此可以判断位置区间P1-1中必有一个磁极；同理得到位置区间P5-11中也有一个磁极。

根据极性编码1001/0000/00得到传感器S1-1输出的磁场值大于零，因此位置区间P1-1中的磁极为N极；同理，位置区间P5-11中的磁极也为N极。传感器S1-3，S2-3，S3-3，S3-4输出的磁场值皆小于零，因此位置区间P3-6中的磁极为S极；同理得到位置区间P7-6中的磁极也为S极。

2)当N磁极中心位于位置区间P1-4、P5-10，S磁极中心位于位置区间P3-10、P7-4时，此时传感器阵列24编码为1000/0010/0010/1000/1111/1111。将24位编码排布成如下形式，如图11。

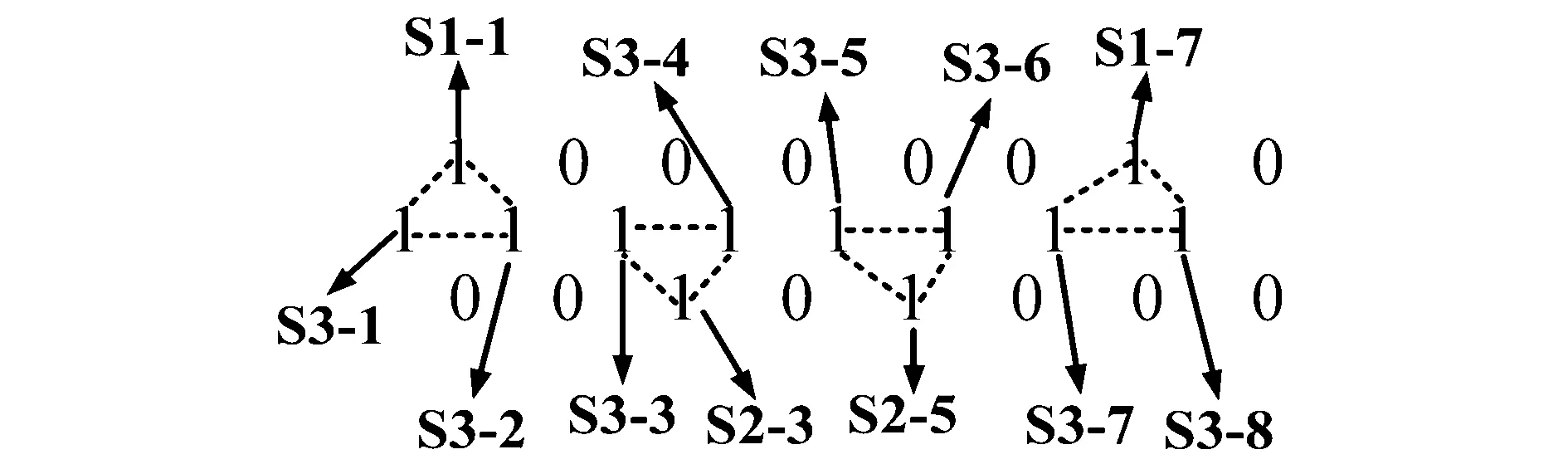
图11 编号信号与传感器之间的关系Fig.11 Relationship between number signal and sensor

由图11可以得出传感器S1-1、S1-7、S2-3、S2-5、S3-1、S3-2、S3-3、S3-4、S3-5、S3-6、S3-7和S3-8输出信号为1。其中S1-1、S3-1和S3-2相邻组成了三角形，在位置区间P1-4中必有一个磁极。再根据极性编码1001/1100/1100得到传感器S1-1，S3-1和S3-2输出的磁场值皆大于0，因此位置区间P1-1中的磁极为N极；同理得到位置区间P5-10中为N极、P3-10和P7-4中为S极。

依据传感器输出信息对转子位置判断的基本流程如图12所示。

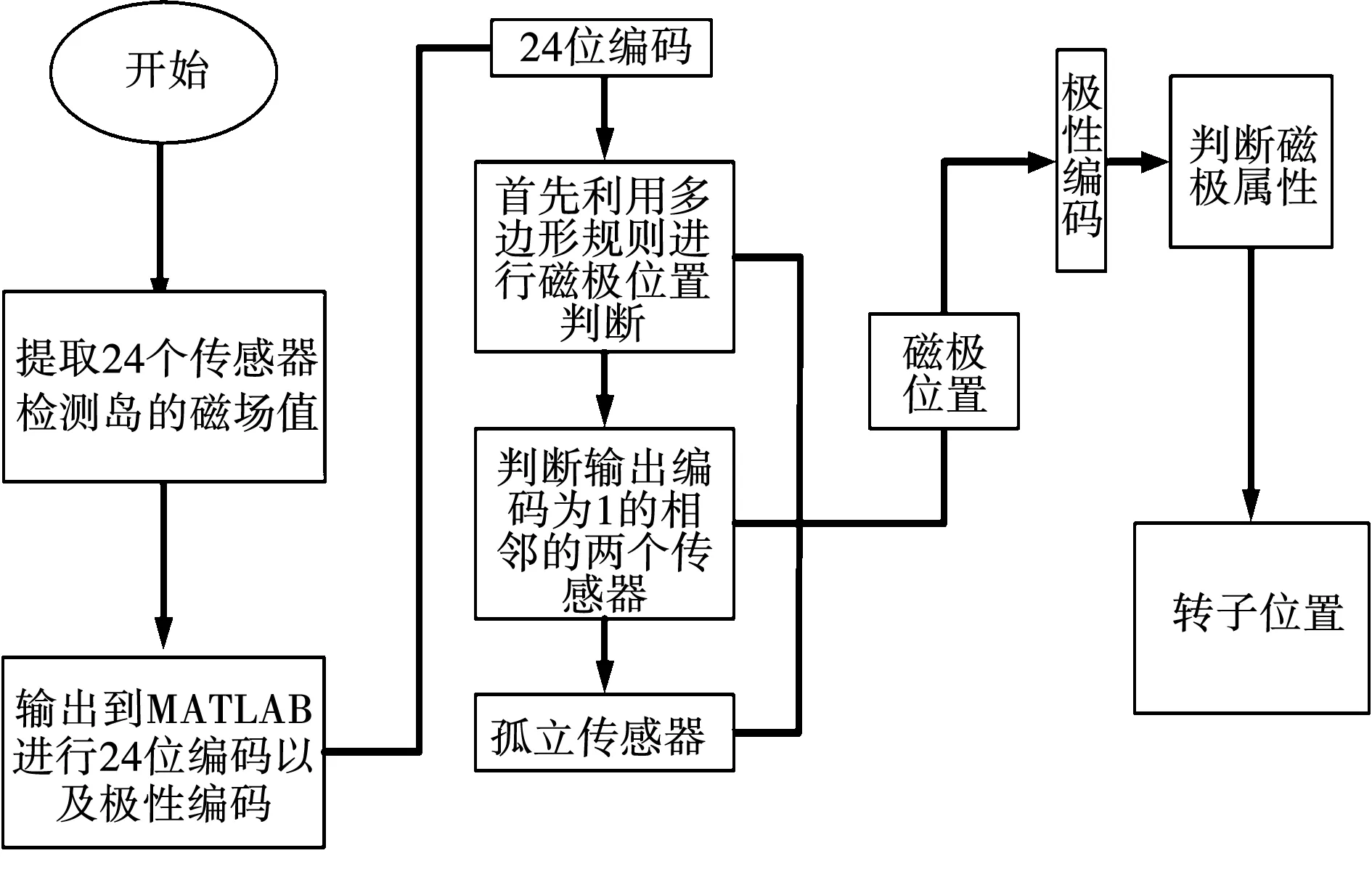
图12 球形电机转子位置检测整体流程图Fig.12 Overall flow chart of spherical motor rotor position detection

将输出编码为1的传感器进行多边形组合步骤中，其中多边形要求有以下几点：

1)在多边形区域内不能存在独立的霍尔传感器；

2)在边线上只允许两端点存在霍尔传感器；

3)多边形与多边形之间不存在公共的顶点和边；

4)多边形的所有内角αi≤90°；

5)四边形优先级要大于三角形。

输出为1的所有传感器尽可能多的划分成多边形，以多边形为一个整体来判断转子磁极的位置。如果剩余输出编码为1的传感器之间不能构成多边形，则首先判断相邻的两个传感器，然后再判断孤立的传感器。得到所有磁极所位于的位置区间后通过极性编码判断磁极极性。

5 实验验证

本实验通过利用Modbus通信协议来实现无线传输模块之间的通信，控制三轴转台旋转。利用3D打印技术制作了传感器支架以及球形电机样机壳，通过控制电机旋转，传感器的输出数据经过FPGA处理在MATLAB中绘制图像。

实验所用到的主要参数如表4所示，实验装置如图13所示。

表4 主要参数

图13 实验装置图Fig.13 Experimental platform

在实验过程中，控制电机1和电机2旋转到指定的角度。经过传感器采样和FPGA数据处理，可以得到在理论位置下传感器的输出信号，对其中几个特殊位置进行实验验证。

在实验过程中，考虑到旋转空间的因素，本文只对上半球面的传感器S1-1至S1-8、S3-1至S3-8进行验证，并且根据转子磁极的对称性，传感器的编码信号和磁场数据满足以下条件：C1-1=C2-5、C1-2=C2-6、C1-3=C2-7、C1-4=C2-8；B1-1≈B2-5、B1-2≈B2-6、B1-3≈B2-7、B1-4≈B2-8。因为实验中并没有考虑定子线圈的影响，所以规定传感器测量到的值B2-1=B1-5，B2-2=B1-6，B2-3=B1-7，B2-4=B1-8，B2-5=B1-1，B2-6=B1-2，B2-7=B1-3，B2-8=B1-4。因为阈值设置为0.029T，根据传感器的灵敏度，传感器输出阈值电压为0.377 V。对上述理论进行了部分仿真验证。

验证一：当转子位于初始位置时，X正半轴穿过传感器S3-1，Y正半轴穿过传感器S3-3。此时N磁极中心位于位置区间P8-14和P4-14，S磁极中心位于位置区间P2-14和P6-14。根据分析只有传感器S3-1、S3-3、S3-5、S3-7输出编码为1，并且相互不能构成多边形。验证传感器S3-1、S3-3、S3-5、S3-7的输出信号如图14。

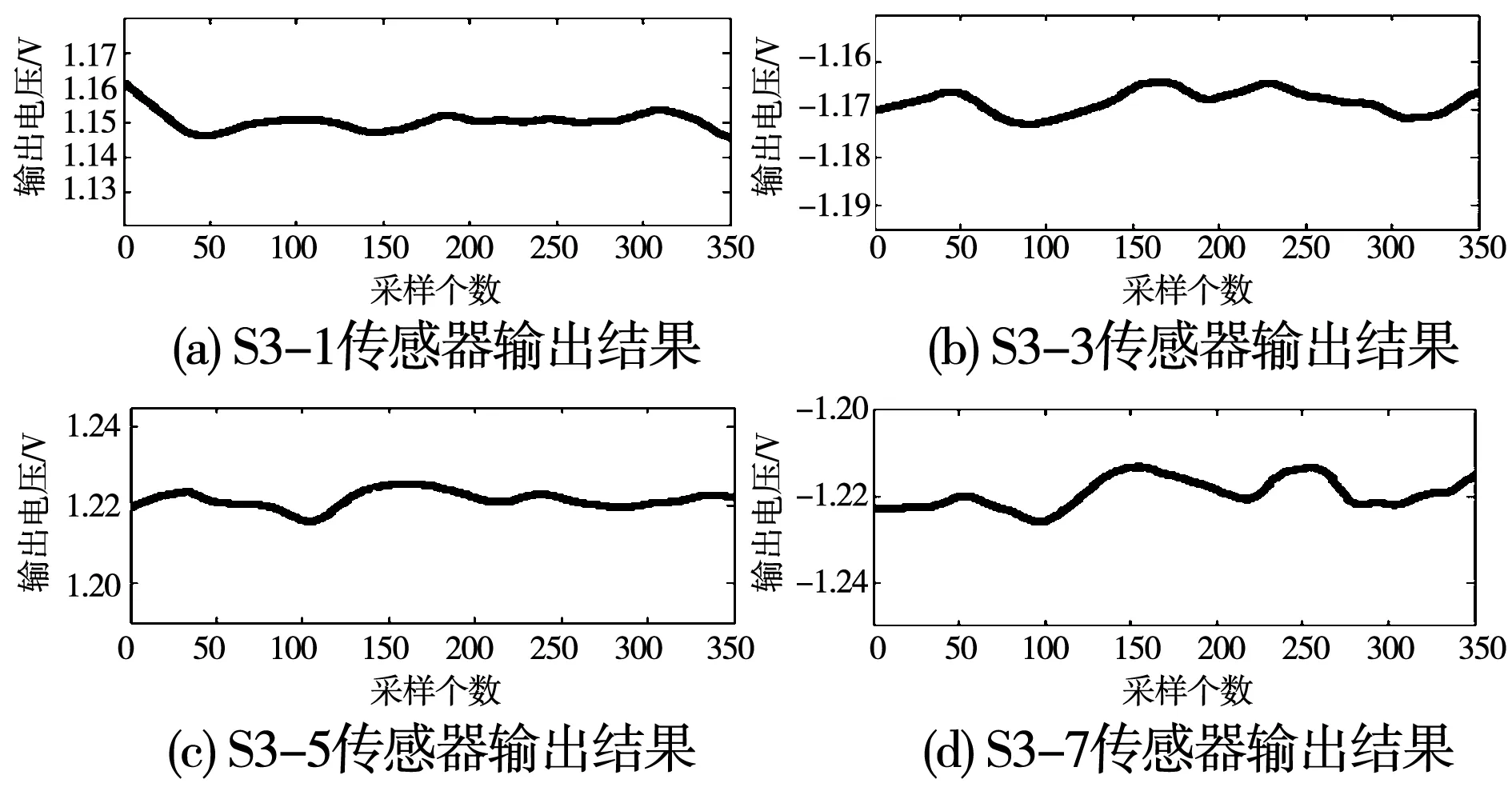
图14 传感器的输出信号图Fig.14 Outputsignal diagram of sensors

剩余12个传感器的输出信号如图15所示。

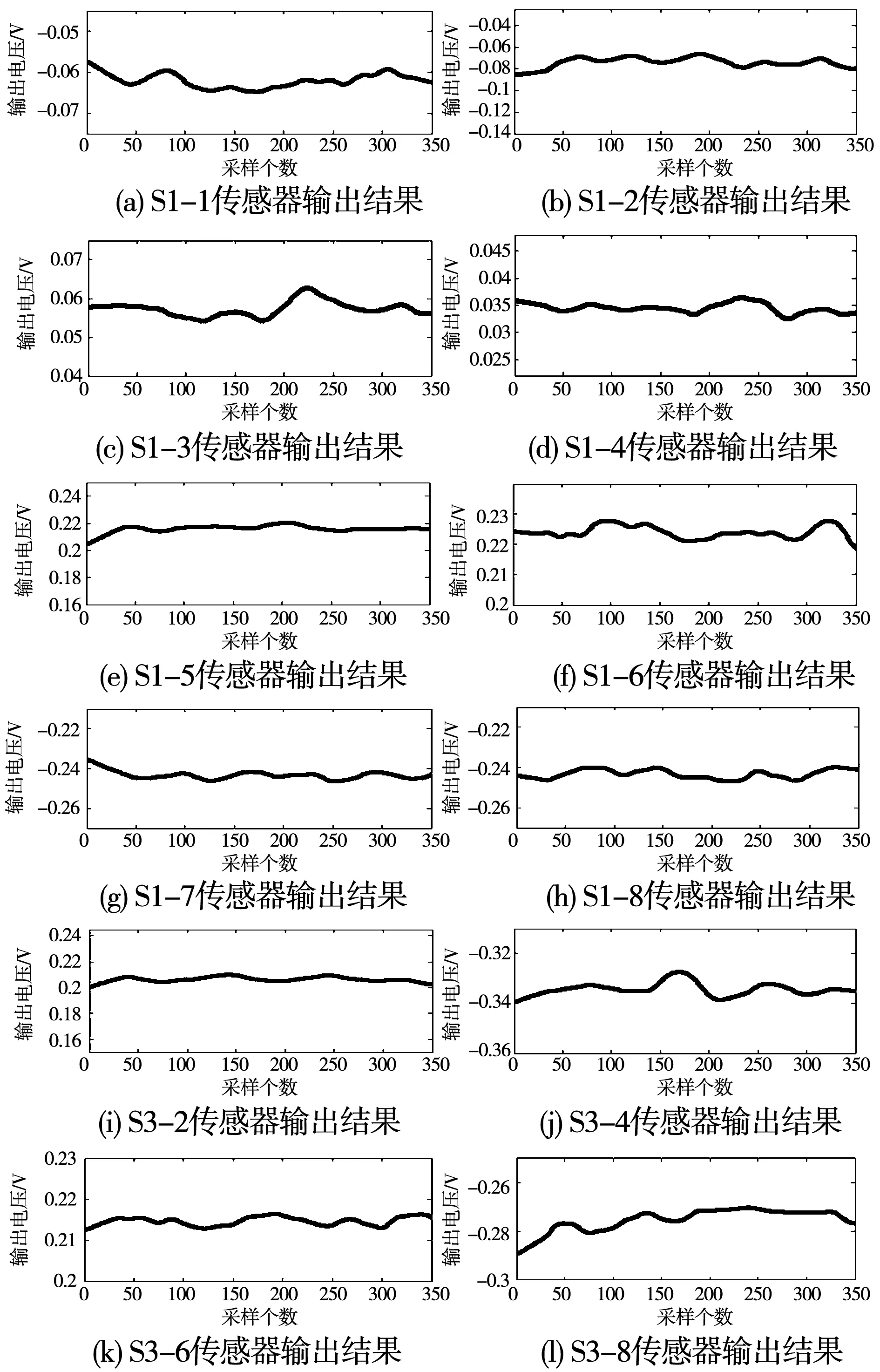
图15 传感器的输出信号图Fig.15 Output signal diagram of sensors

经过与阈值电压0.377 V比较，传感器S3-1、S3-3、S3-5、S3-7输出编码信号为1，剩余传感器的输出编码皆为0，因此可以得到传感器S1-1至S1-8、S3-1至S3-8的输出编码为0000/0000/1010/ 1010，根据对称性得到24位编码为0000/0000/ 0000/0000/1010/1010。极性编码为1010，通过判断规则得出N磁极中心位于位置区间P8-14和P4-14，S磁极中心位于位置区间P2-14和P6-14。结果与理论分析基本相符。

验证二：当转子由初始时刻绕Z轴旋转22.5°，使得N磁极中心为位置区间P1-6和P5-6，S磁极中心为位置区间P3-6和P7-6。根据分析得传感器S1-1、S1-3、S1-5、S1-7、S3-1、S3-2、S3-3、S3-4、S3-5、S3-6、S3-7、S3-8输出编码为1，剩余4个传感器的输出信号为0。其输出信号如图16。

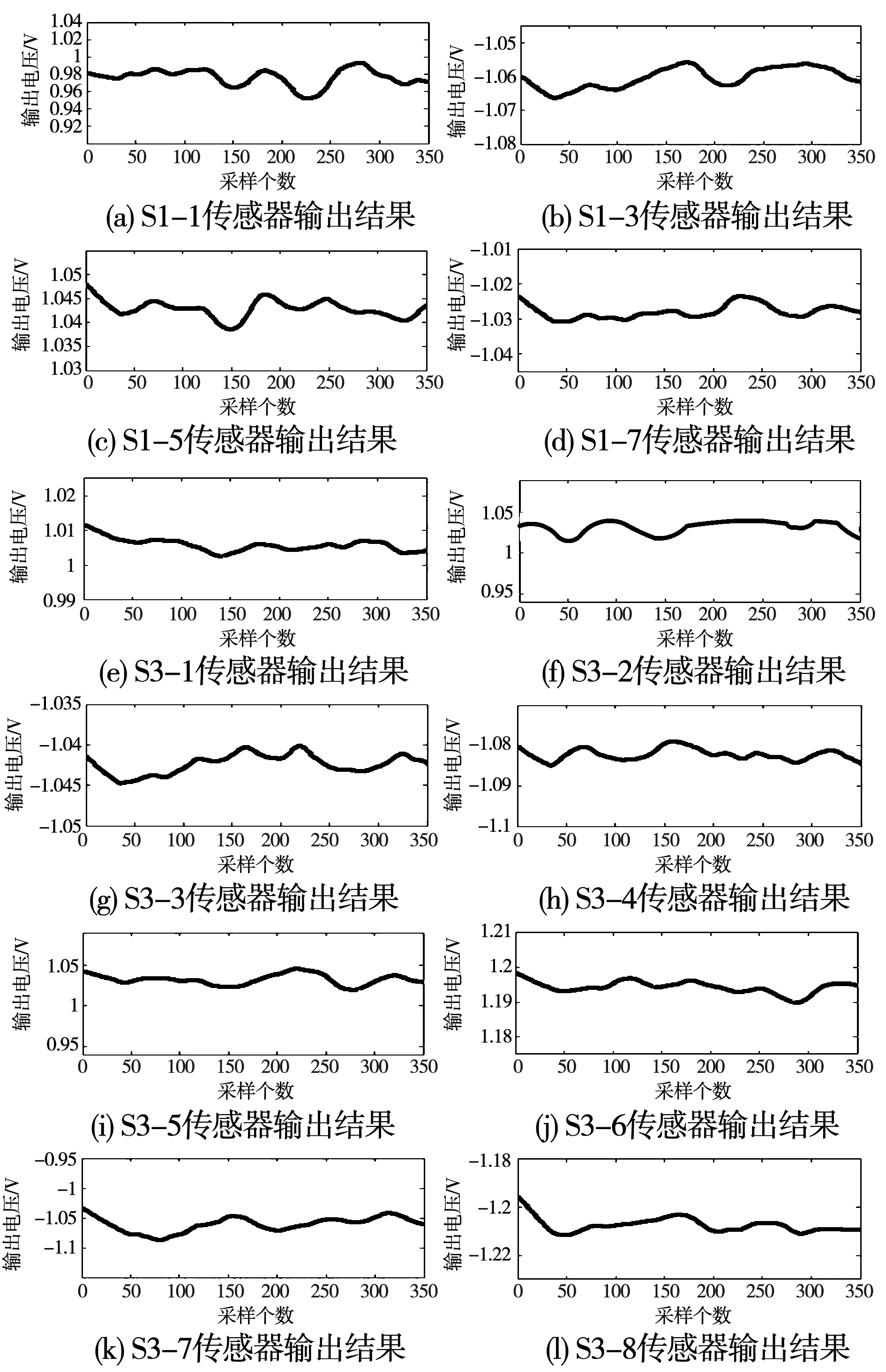
图16 传感器的输出信号图Fig.16 Output signal diagram of sensors

剩余4个传感器的输出信号为0，其输出信号如图17所示。

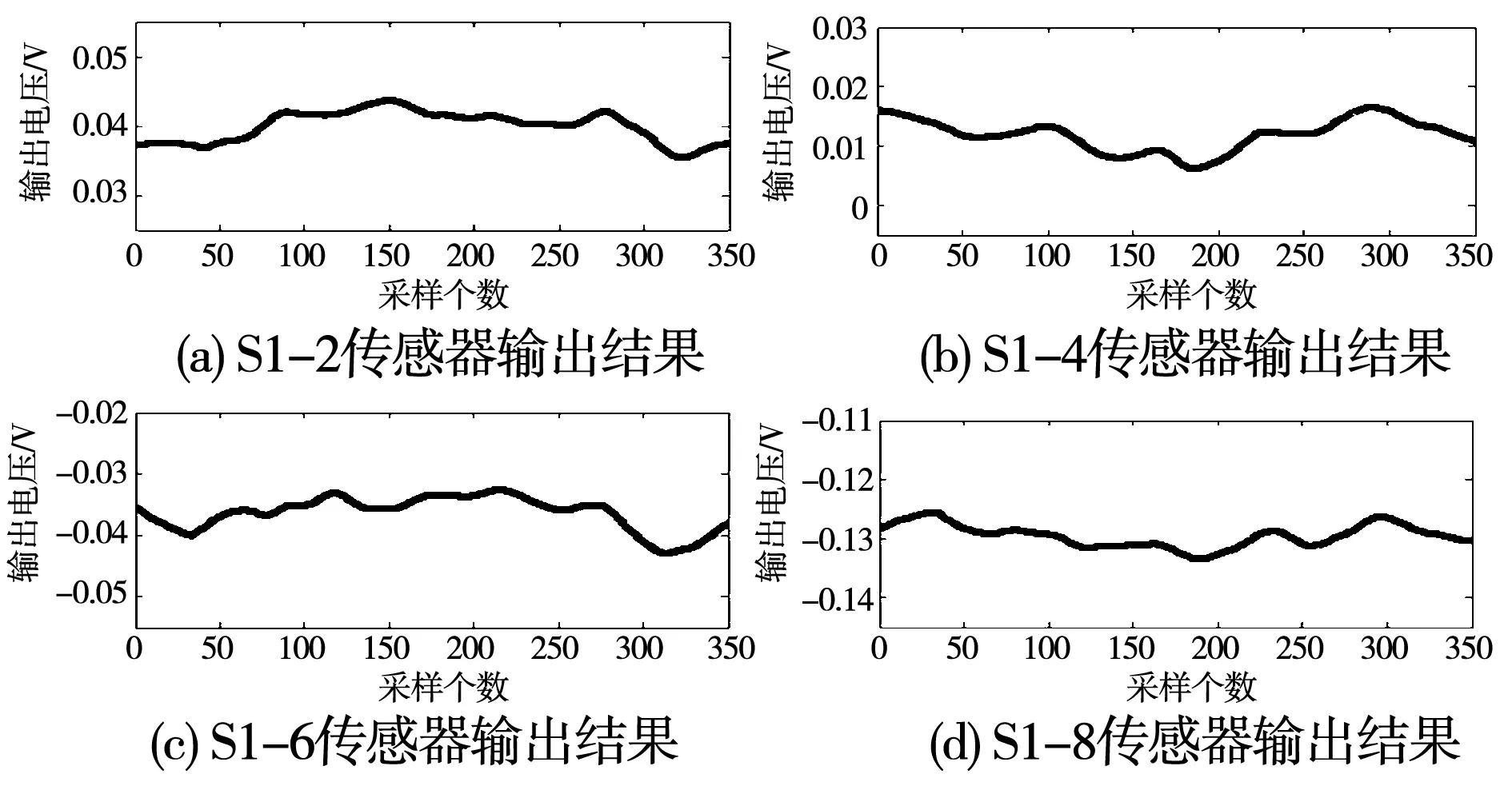
图17 传感器的输出信号图Fig.17 Output signal diagram of sensors

经过与阈值电压0.377V比较，传感器S1-1、S1-3、S1-5、S1-7、S3-1、S3-2、S3-3、S3-4、S3-5、S3-6、S3-7、S3-8输出编码信号为1。剩余的输出编码皆为0，因此可以得到传感器S1-1至S1-8、S3-1至S3-8的输出编码为1010/1010/1111/1111，根据对称性得到24编码为1010/1010/1010/1010/1111/ 1111，极性编码为1010/1010/1100/1100，通过本文的判断规则进行判断得出N磁极中心位于位置区间P1-6和P5-6，S磁极中心位于位置区间P3-6和P7-6，结果与理论分析基本相符。

6 结 论

本文研究了一种基于霍尔传感器阵列的永磁球形电机转子位置辨识方案。根据转子磁场的分布特点同时考虑定子线圈的影响来确定传感器输出编码的转换阈值，依据转化阈值定子球面进行划分，来确定霍尔传感器的安装位置及数量。最后根据霍尔传感器的24个输出编码以及极性编码确定转子磁极所在的位置，从而实现对转子的位置辨识。文中的转子辨识理论简单，所需的霍尔传感器数量不多，需要处理的数据量不大，因而对处理器性能要求不高。同时本文提出的转子辨识方案易于实现嵌入式转子位置辨识系统，利于永磁球形电机向小型化、微型化发展。但本文的研究成果还处于转子的位置区间辨识，后续将进一步开展辨识区间内的研究，最终确定转子的精确位置。