矢量控制下的车用永磁电机电磁振动特性分析

洪剑锋，王善铭，孙旭东，孙宇光，曹海翔

(清华大学 电力系统国家重点实验室，北京 100084)

0 引 言

电动汽车用永磁同步电动机的电磁振动噪声水平直接影响着电动汽车的噪声、振动与声振粗糙度(noise vibration harshness，NVH)性能。国内外学者针对车用永磁电机的电磁振动问题开展了大量研究，总结如下。

在车用永磁同步电机的振动噪声机理研究方面，基本都从电机定子三相电流出发进行磁场、电磁力和电磁振动噪声的计算。文献[1-2]采用解析法详细分析了表贴式永磁电机电磁振动特性和噪声的预估方法。文献[3]采用有限元法对6种不同齿槽配合永磁电机的电磁振动进行分析，结果表明两倍频电磁振动较大。文献[4-5]用解析法和有限元法对车用永磁同步电机径向电磁振动特征，并指出了影响电磁振动的相关因素。文献[6]提出了一种基于模态叠加法的车用永磁电机电磁振动估算方法。文献[7]采用半解析模型计算了考虑电流谐波的永磁同步电机的定子表面振动和噪声。文献[8]对电流的影响进行了详细研究，认为谐波电流会影响电磁力和电磁振动，指出谐波电流的相位是影响的关键。文献[9-10]对永磁电机磁场和电磁力进行了仿真，结果表明，电机中的电磁力随着负载的增加而增加，但文中并未对引起的原因进行解释。文献[11]对异步电机在不同负载工况下的电磁振动进行了实验测试，结果表明电机在不同的负载工况下呈现不同的规律，但是并未深入探究。

在汽车用永磁电机的减振降噪方面，主要从设计和控制两个角度出发。文献[12]针对V型转子永磁电机的电磁振动，提出一种新型隔磁桥的减振优化方案。文献[13]采用转子分段斜极，文献[14]采用斜槽方案通过降低电机中的转矩脉动降低电磁振动。文献[15]通过在转子齿上开槽来降低齿槽转矩和电磁振动。文献[16]以转矩脉动和电磁力最小为目标，对转子铁心结构进行优化来降低电磁振动。文献[17]提出齿顶偏移结构来降低电机中2倍电流频率电磁振动。文献[18]提出一种场重构法，通过优化电机电流波形，使得电磁转矩和径向力波动最小。文献[19-20]采用在电机定子中注入补偿电流的方案来降低2倍电流频率电磁振动。虽然这些方案具有一定的可行性，但是并未从矢量控制的角度进行分析和阐述，故不利于对低振动控制方案的指导。

因此，目前针对电机振动的研究，均从定子三相电流出发而不是dq轴电流出发推导电磁力特性，这不仅不利于从矢量控制出发开展电机控制方案设计，也不利于对负载下的电机电磁振动进行分析。基于此，本文从矢量控制的角度出发对永磁电机的电磁振动机理进行分析，致力于探究负载工况下永磁电机的电磁振动规律，并对低振动永磁电机电磁振动的矢量控制方案进行指导。

1 矢量控制下的电机电磁力分析

对于电动汽车驱动用永磁同步电机而言，不论是运行在基速下的恒转矩区，还是基速上的恒功率区，常采用矢量控制对其进行驱动。矢量控制的本质是将电机的定子电流解耦为转矩电流分量iq与励磁电流分量id，分别实现对电机的转矩和磁链的控制，使得永磁电机获得良好的动态性能。当电机工作在非饱和状态时，电机中的气隙磁场Bg可近似为d轴、q轴电流和永磁体产生磁场的叠加，即

Bg(θ,t)=BPM(θ,t)+Bad(θ,t)+Baq(θ,t)。

(1)

式中：BPM为永磁体产生的磁场；Bad为d轴电流id产生的磁场；Baq为q轴电流iq产生的磁场。当忽略齿的影响时，磁场表达式可以写成：

(2)

(3)

Cpωrt}。

(4)

式中：θ为气隙中的空间机械角度；p为电机极对数；Bn为永磁体产生的n次谐波磁场幅值；Badv和Badq为绕组电流产生的v次谐波磁场幅值。当v=6k+1时，C为1；当v=6k-1时，C为-1。

图1给出了永磁体产生的气隙磁场及其谐波分布。由图可知，含量主要为基波及奇次谐波分量。图2为dq轴坐标系下由绕组dq轴电流产生的气隙基波磁场分布结果。

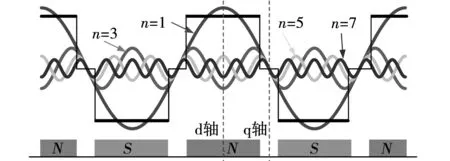
图1 永磁体产生的磁场Fig.1 Magnetic field excited by PM

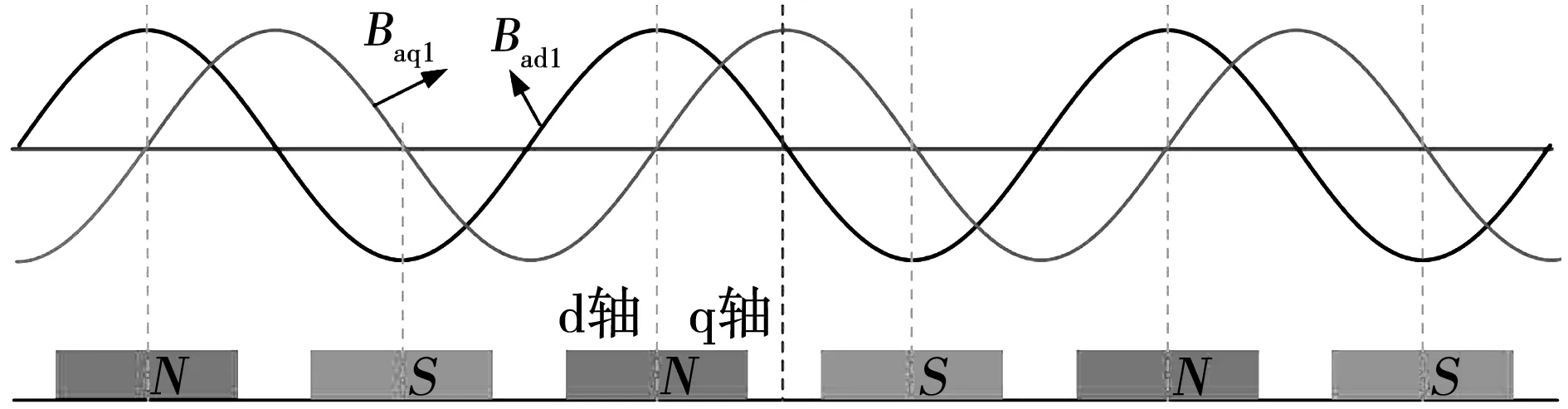
图2 绕组电枢反应产生的磁场Fig.2 Magnetic field excited by winding current

根据麦克斯韦应力张量法，可得引起电机振动的径向力波为

(5)

式中：

(n1±n2)pωrt]；

(C1±C2)pωrt]；

(C1±C2)pωrt]；

(n±C)pωrt]；

(n±C)pωrt∓π/2]；

(C1±C2)pωrt∓π/2]。

当只考虑永磁体和绕组电流产生的基波磁场时，则式(1)可以简写成

Bg(θ,t)=Bd(θ,t)+Bq(θ,t)。

(6)

式中：

Bd=(B1-Bad1)cos(pθ-pωrt)；

Bq=Baq1cos(pθ-pωrt-π/2)。

由此，气隙中的电磁力波式(5)可以写成

Fmcos(2pθ-2pωrt-φ)。

(7)

式中：

由式(7)可知，电机气隙中二倍频电磁力波与永磁体和绕组电流产生的磁场有关。图3为电磁力波随绕组产生的dq轴磁场分布变化，永磁体产生的基波磁场幅值为0.8T。由图可知，当磁场Bad1为0(即id=0)时，电磁力波幅值随着交轴磁场Baq1的增加而增加。由此可知，随着电机负载的增加，电磁力波幅值也将增加，这会导致电机的二倍频电磁振动也增加。在交轴磁场Baq1一定时，电磁力波随着直轴磁场Bad1的增加而减少。这是由于电机此时工作在去磁工况，d轴磁场减小，从而导致电磁力波的幅值降低，这使得电机的电磁振动将会降低。

②由于系统中各因素的数据量纲不尽相同，不能进行比较，故进行灰色关联度分析首先要进行无量纲化的数据处理。

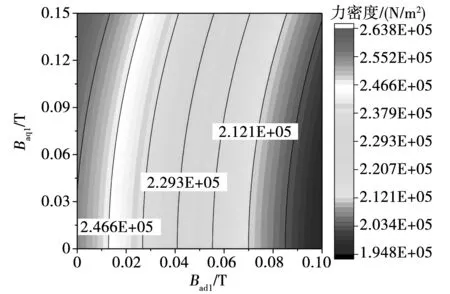
图3 力密度随着dq轴磁场变化情况Fig.3 Force density changing with dq-axis magnetic field

由于径向电磁力是主要的径向电磁振动源，因此，对电机定子齿部集中电磁力进行分析，作用在第i个齿上的径向集中力Fr,i(t)可以表示为

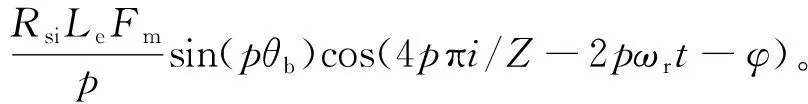
(8)

2 仿真分析

利用2D电磁场和3D结构场对一台6极36槽永磁同步电机的电磁力和定子电磁振动进行仿真，样机参数见表1，具体仿真流程如图4所示。

表1 电机模型的参数

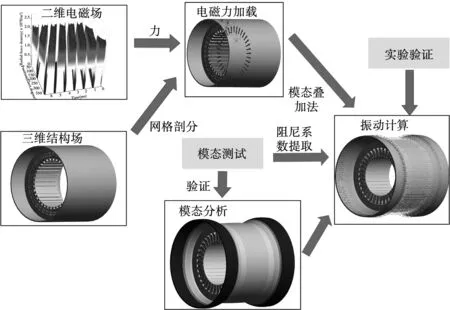
图4 电机电磁振动有限元分析流程Fig.4 Vibration calculation procedure of the motor

首先采用二维有限元法对电机的磁场和电磁力进行计算，得到各个齿上的径向力的幅值、频率和相位信息，其次在三维结构场中对电机的模态参数进行分析，模态求取的准确度将对振动计算有重要影响。再次，根据模态测试实验，得到电机的阻尼比。最后在三维结构场中，将各齿上的电磁力分别进行加载，采用谐响应分析，即模态叠加法对电机的电磁振动进行求解。仿真的电机模型考虑了定子铁心、定子绕组，电机外壳结构，具体的材料特性参数如表2所示。

表2 电机材料特性参数

图5为某一时刻电机在空载和负载Te=8 N·m工况时，沿靠近定子一层的气隙单元圆周的径向气隙磁场的分布及其谐波分量。由图可知，气隙中的谐波分量次数主要为基波及其奇数倍谐波。此外，当电机加载时，由于q轴磁场的引入，电机的空间磁场相位会发生偏移。而后，采用麦克斯韦应力张量计算了转子不同位置时电机气隙中的径向电磁力，对其在时间和空间上进行分解，图6给出了二倍电频率下的电磁力波空间分布结果。

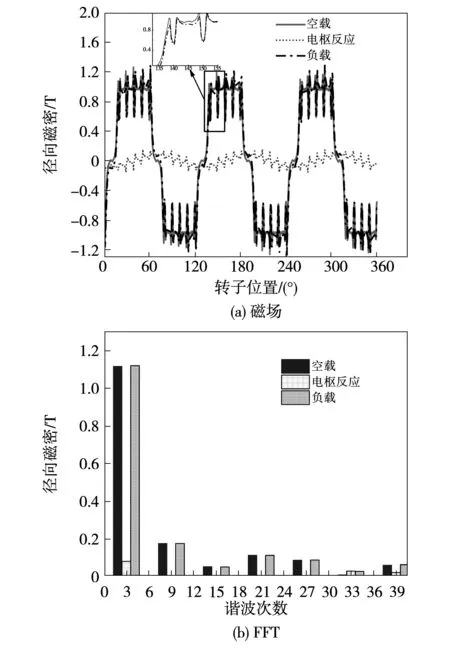
图5 负载Te=8 N·m时的磁场分析Fig.5 Air-gap flux distribution when Te=8 N·m

由图6可知，当电机加载时，电机气隙中二倍频模数为6的电磁力波幅值从空载的167.5 kN/m2增加到负载时的170.0 kN/m2。此外，其相位也发生一定的偏移，这说明前面理论分析的正确性。

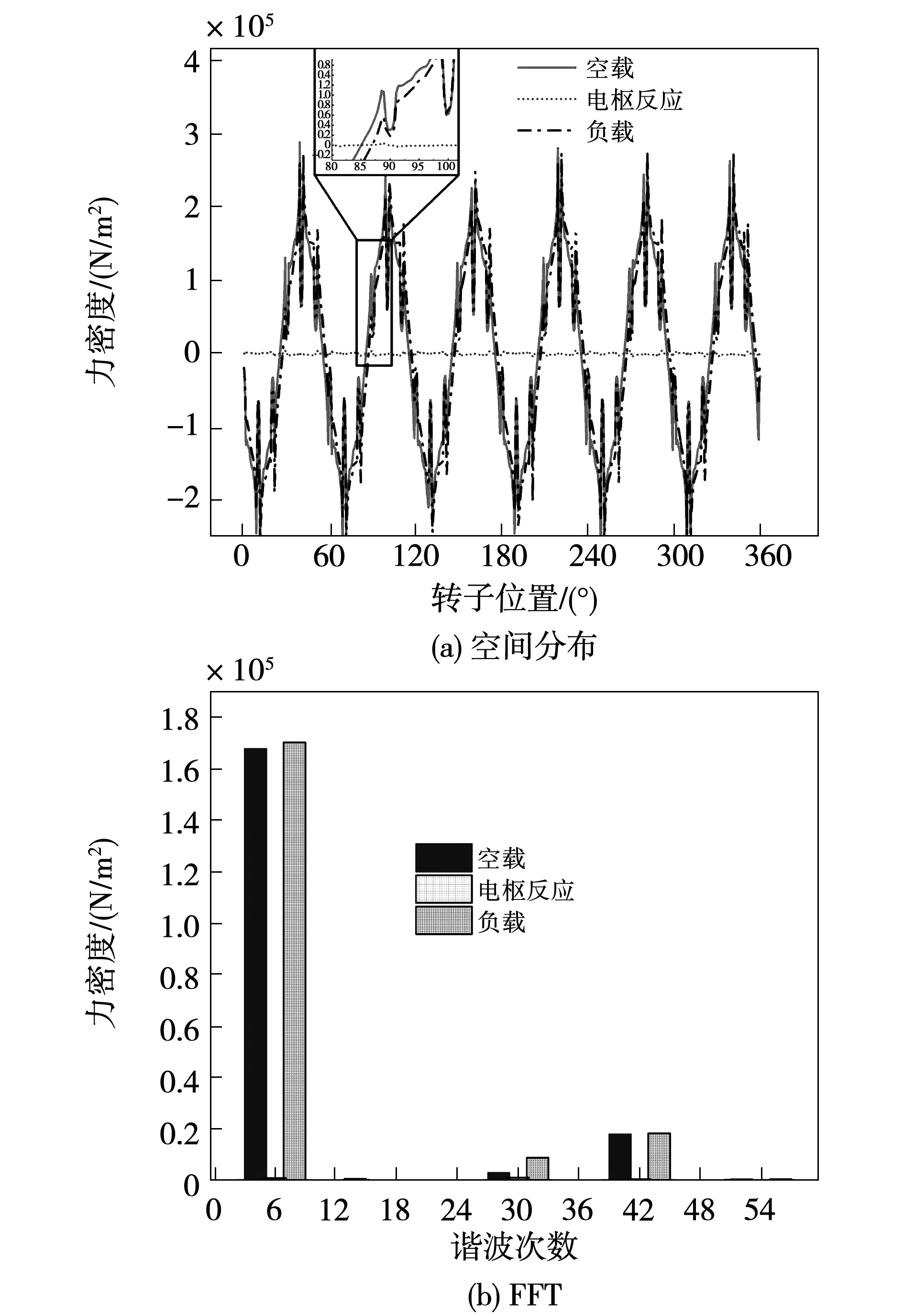
图6 负载Te=8 N·m时的二倍电频率电磁力波Fig.6 Radial force distribution when Te=8 N·m

为了进一步分析电机负载的影响，图7给出了id=0控制方案下，电机电磁转矩从0～18 N·m变化时，二倍电频率模数为6的电磁力波幅值变化曲线。结果表明负载增加时，电磁力波幅值也逐渐增加。

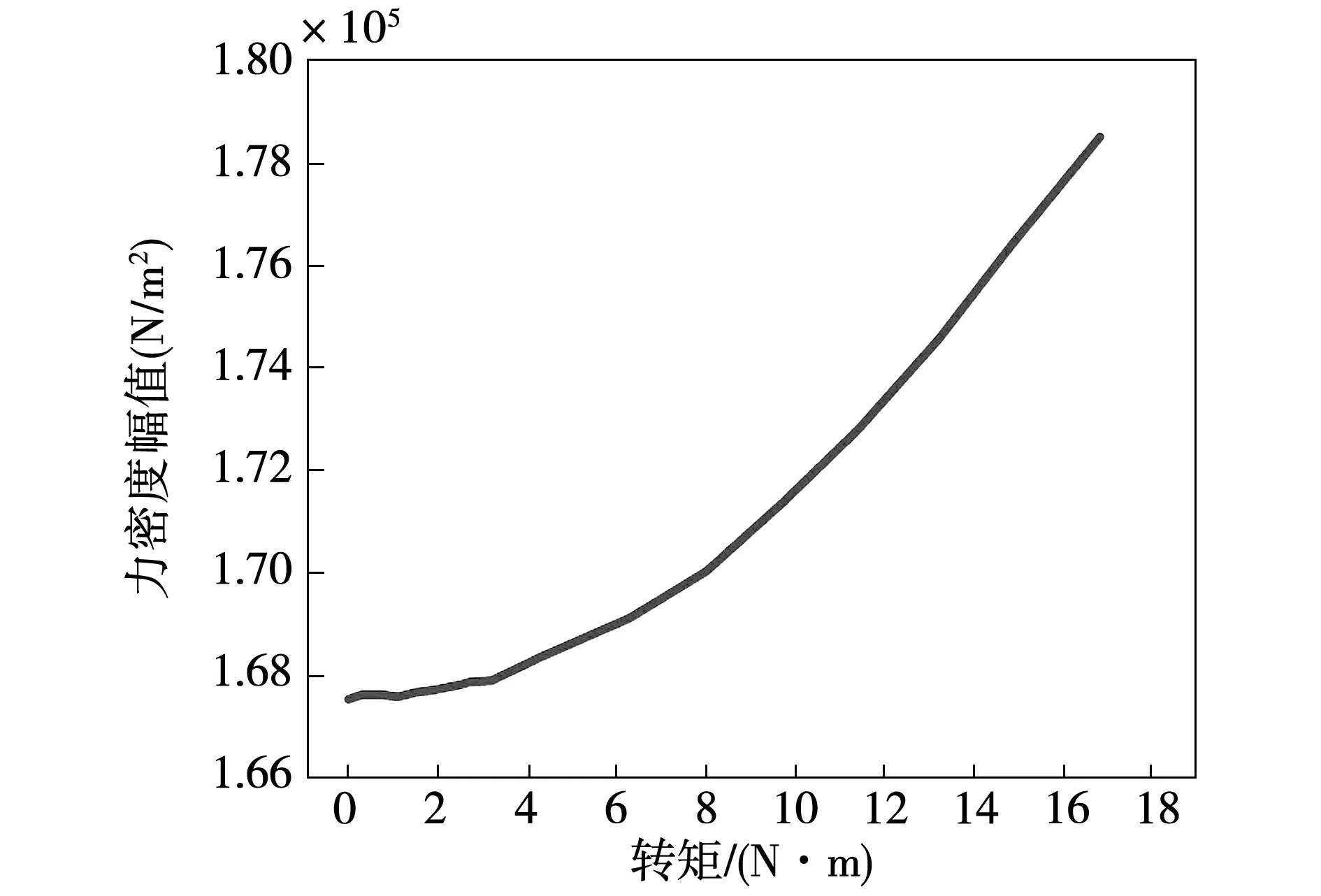
图7 不同负载下二倍频电磁力密度幅值Fig.7 Force density at twice fundamental frequency varying with different loads

图8给出了不同iq电流激励下定子单齿上的径向电磁力结果。由图可得，作用在定子齿部的二倍电频率集中力，其幅值随着q轴电流的增加而增加。进一步地，图9分析了id电流对定子齿部径向电磁力的影响，图中id电流为负值，表明其产生的磁场与永磁体产生的磁场相位相反。由图可看出，在保持q轴电流不变时，增加d轴电流，将使作用在定子齿上的二倍频电磁集中力逐渐降低，这主要由d轴电流产生的去磁磁场作用的增强导致的结果。

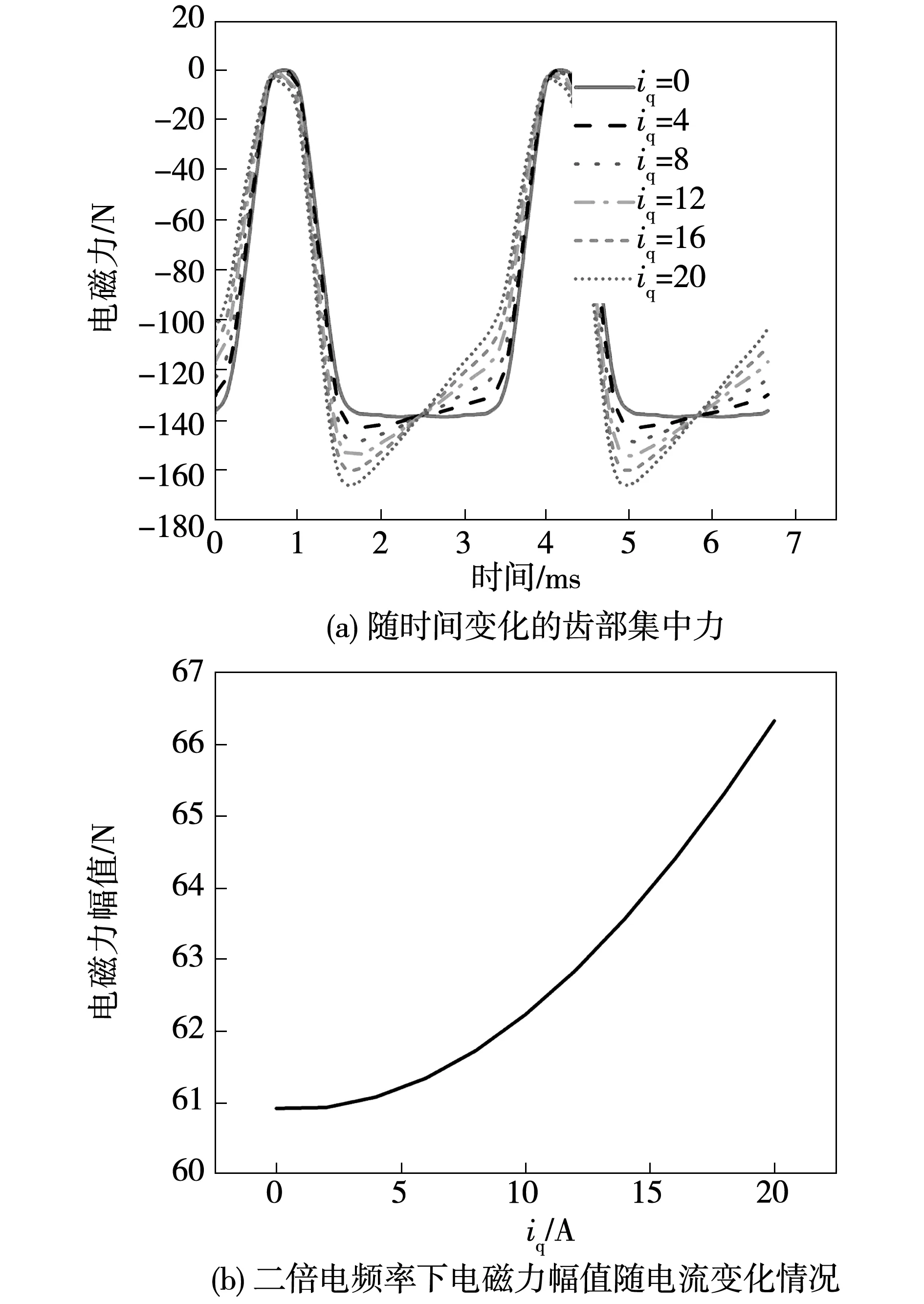
图8 不同iq电流下的齿部电磁集中力Fig.8 Concentrated tooth force varying with iq

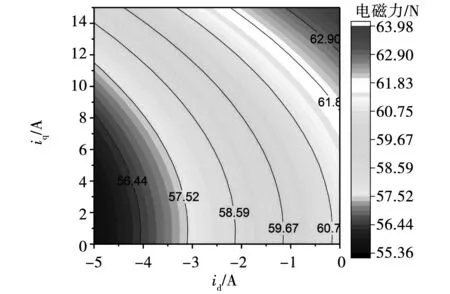
图9 不同id,iq电流下的齿部电磁集中力Fig.9 Concentrated tooth force varying with id and iq

图10为不同d、q轴定子电流下永磁电机的电磁转矩结果，随着q轴电流iq的增加，电磁转矩逐渐上升。而随着d轴电流id的增加，电机中的电磁转矩降低，但降低幅值不大。

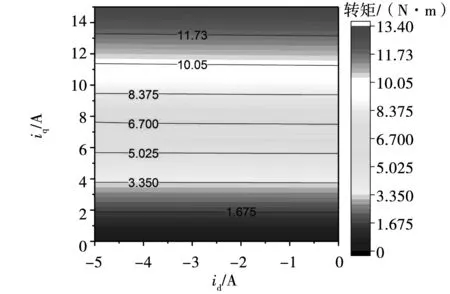
图10 不同电流下的电机电磁转矩Fig.10 Electromagnetic torque varying with id and iq

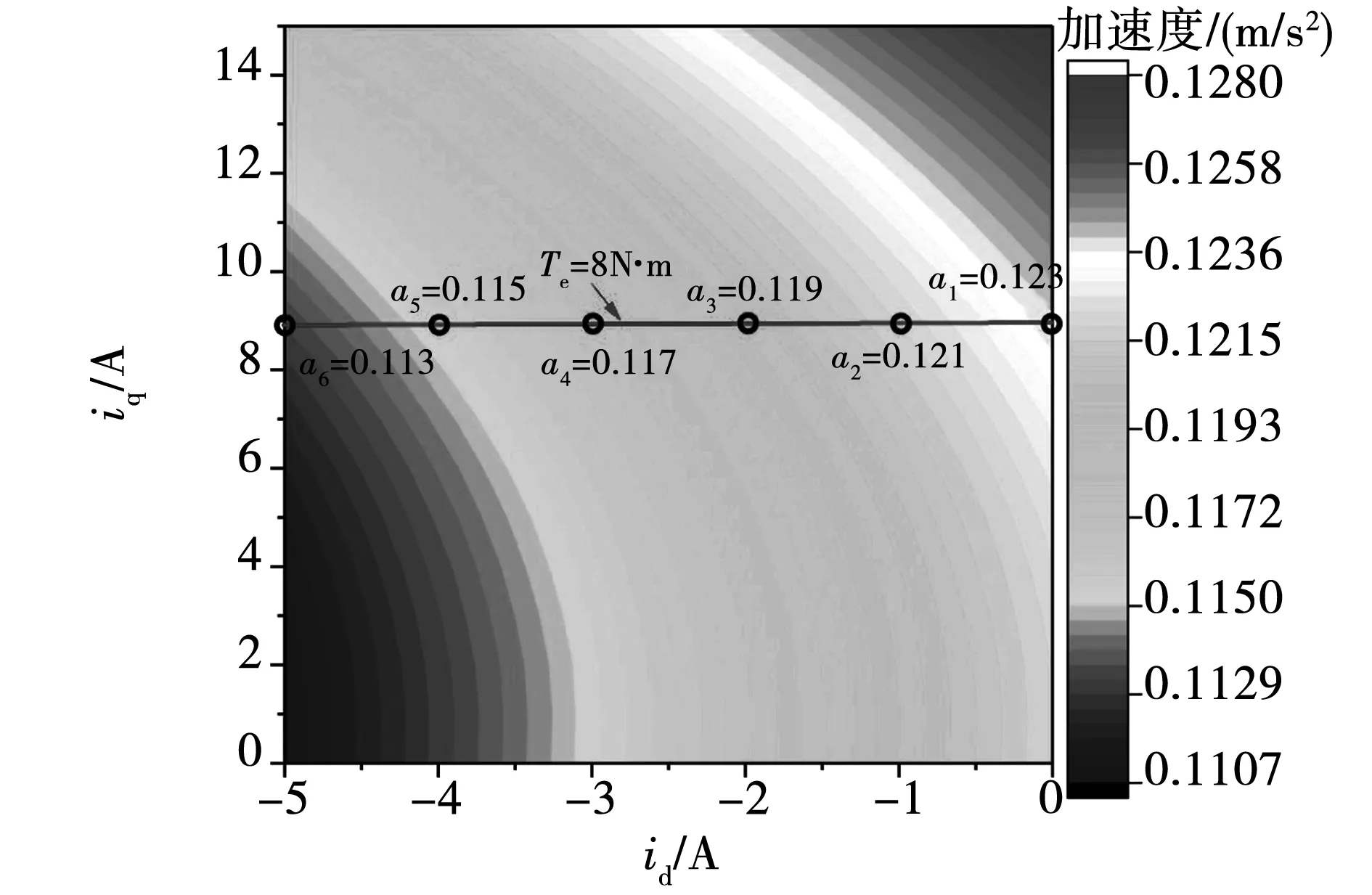
图11 不同id、iq电流时的电机电磁振动Fig.11 Motor vibration varying with id and iq

由此可知，从电机的转矩-电流关系图和电磁振动加速度-电流关系图中，在保证相同电磁转矩输出的前提下选择合适的d、q轴电流分量以寻求电机的二倍频电磁振动较小。

3 实验验证

为了对理论分析和有限元仿真结果进行验证，对一台6极36槽永磁电机进行了实验测试。实验中，采用id=0的电机控制方案。图12为样机振动测试平台，电机通过联轴器与负载机相连，固定在台架上。采用型号为PCB 356A32型号的加速度传感器采集电机机壳表面的电磁振动，采用西门子的SCM205数据处理系统对采集的数据进行处理。采用变频器对永磁电机进行驱动，测量不同转速不同负载工况下电机表面的振动加速度值。图13为电机运行在1 500 r/min、负载为6 N·m时的电机相电流波形。

图12 实验装置Fig.12 Test rig

从图13可看出，相电流中主要为基波电流，此外，还有3、5、7次谐波电流，但相对于基波电流而言，其幅值均较小，可忽略。图14给出了此种工况下电机的电磁振动波形。

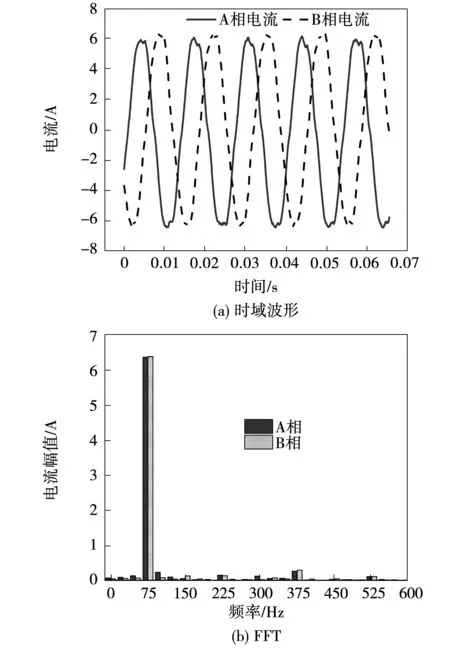
图13 电机在1 500 r/min转矩6 N·m时的电流波形Fig.13 Measured stator currents of the motor at 1 500 r/min under Te=6 N·m

由图14可知，电机在两倍电频率(150 Hz)处的振动加速度为0.12 m/s2，大于其他频率下的振动加速度。为了对负载的影响进行验证，完成了3种转速(900、1 200和1 500 r/min)6种负载(转矩1～6 N·m)工况下的电机振动测试，二倍电频率下的振动加速度幅值结果如图15所示。由图可得，在同一个转速下，随着电机负载的增加，电机电磁振动幅值也增加，这验证了理论分析和仿真结果。此外，对于同一个负载而言，当转速越高，电机的电磁振动越大。

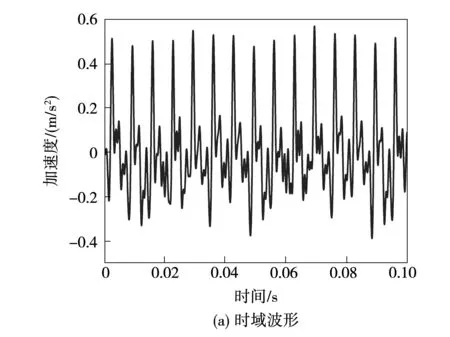
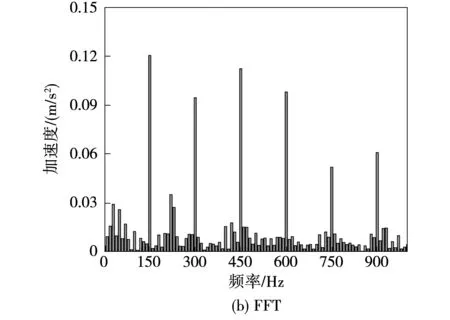
图14 电机在1 500 r/min转矩6 N·m时的电磁振动加速度Fig.14 Measured vibration acceleration of the motor at 1 500 r/min under Te=6 N·m

图15 电机在不同转速转矩下的电机二倍频电磁振动Fig.15 Measured vibration acceleration at twice fundam-ental frequency of the motor at different speed and toque

4 结 论

本文从矢量控制的角度分析了永磁同步电机的电磁振动规律，基于磁场定向的理论分析了电机在负载工况下的电磁力和电磁振动特点。采用多物理场有限元仿真研究和实验分析电机不同转速下的电机振动规律，对理论分析结果进行了验证，得到以下结论：

1)随着电机负载增加(q轴电流的加大)，气隙磁场中的基波含量增加，导致二倍频下的电磁力增加，从而加剧了电机的电磁振动。

2)不同d、q轴电流将导致不同的电机电磁振动和电磁转矩，可以通过选择合适的d、q轴电流以使电机的电磁振动降低。

本文的研究成果有利于在矢量控制方案中直接控制d、q轴电流分量来达到控制电磁力和电磁振动的目的，可以在电机设计和控制阶段评估电机的电磁振动性能。