基于时频域的变分模态分解油气检测技术及应用

张 舜， 周怀来,2， 王元君,2， 周玉毅， 韦 豪

(1.成都理工大学 地球物理学院，成都 610059； 2.“油气地质及开发工程”国家重点实验室，成都 610059)

0 引言

地震波在地下介质中传播时，受外界摩擦力和地层岩性变化等原因，会伴随着相应的能量与频率的损失和衰减。近年来，大量研究者依照这种衰减属性，结合时频分析技术提取“衰减梯度”进行含气性储层检测的方法，取得了有效的应用效果[1-5]。

Mitchell[6]提出了EAA方法，通过计算高频段拟合斜率来计算衰减吸收系数，但该计算方法仅适用于高信噪比或平稳的频谱，而地震信号高频段中往往掺杂着噪音的干扰，限制了该方法的应用；张固澜等[7]利用改进的广义S变换对低频段进行衰减梯度的提取，并进行了验证，但该方法需要避免强干扰信号的影响，需要事先掌握干扰信号的频率特征；熊晓军[8]使用三参数小波变换获得更高精度的时频谱结合曲线非线性拟合提取衰减梯度，提高了储层预测的可靠性；薛雅娟等[9]将EEMD与小波变换集合，通过提取特征剖面，进一步提取更高精度的衰减梯度，为含气性检测提供了一种新思路；于娅[10]提出了匹配追踪提取高频衰减梯度的方法，其对浅层油气检测更为敏感准确。

Huang[11]提出了经验模式分解(EMD)方法，该方法可以用于对非线性和非平稳信号的分解，但存在端点效应和模态混叠效应；Wu等[12]提出集合经验模态分解(EEMD)作为EMD的一种改进算法，但分解后的残留噪声导致重构误差较大，这也限制了其应用；Yeh[13]进一步改进提出互补集合经验模态分解(CEEMD)，该方法不仅改善了模态混叠而且保证了重构的精确性,但受递归分解方式的影响，不能完全抑制模态混叠现象；Dragomiretskiy[14]提出了变分模态分解(VMD)，VMD弥补了以往模态分解没有数学理论作支撑的弊端，它有着坚实的数学基础做支撑，并通过非递归的方式解决了模态混叠问题，在机械故障、桥梁和地球物理等领域得到了广范应用[15-16]；Zhou[17]应用VMD结合奇异值法对地震数据进行去噪，比起其他方法，该方法去噪效果更高，有效信号保留相对完整；龙丹[18]利用VMD改进的HHT方法，显示了其在突出地质信息方面的时频聚焦的优越性。

笔者受前人研究的启发，提出了利用VMD与高时频分辨率的广义S变换结合来加强含气储层的弱反射信号，从而获得更精确的衰减梯度进行含气检测的方法。通过对实际工区资料的处理，结合实际已知含气性资料及测井数据对本文方法进行了验证。结果表明，本文方法对含气目的层有很好地指示效果和应用价值，有望在以后的油气检测应用中进一步发挥作用和推广。

1 基本原理

1.1 变分模态分解原理

传统的EMD通过递归的方式对非线性信号进行分解，主要依靠对极值点的需找方法，缺少数学理论的支撑，存在严重的模态混叠现象。CEEMD是一种噪声辅助的改进经验模式分解算法。它将一定幅度的正负成对白噪声添加到时间序列，然后由EMD分解并保存结果，改善了EMD的模态混叠现象，但没有改变EMD的递归分解模式的本质。

变分模态分解(Variational Mode Decomposition，VMD)不同于EMD和CEEMD,可以将其看作是多个维纳滤波器的组合，是一种寻找最优解的变分问题。VMD具有坚实的数学基础，它改变了以往经验模态分解类方法递归分解的特征，是一种完全非递归的变分问题分解模型，克制了模态混叠现象。VMD的分解过程是假设每一个分量函数都围绕一个固定的中心频率ωk，通过寻找最优解，围绕中心频率扰动，不断更迭每个模态函数和中心频率，从而使得最终分解的每个模态函数为具有窄带特性的调幅-调频(AM-FM)信号。

调幅-调频信号表示为：

uk(t)=Ak(t)cos(φk(t))

(1)

式中：Ak(t)、φk(t)分别表示各模态函数的瞬时振幅和瞬时相位。

变分模态分解(VMD)主要对信号进行以下变换计算处理[14]：

VMD是一个约束变分问题，由式(2)、式(3)表示。

(2)

(3)

式中：δ(t)为狄里克莱函数；uk(t)为第K个模态函数。

每个模式的带宽由解析信号的L2范数决定。引入二次罚项α和拉格朗日乘子λ，将式(2)的约束问题转化为非约束问题：

(4)

式中：α为惩罚因子；f(t)为输入信号；λ(t)为Lagrange函数。

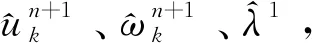
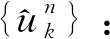
(5)

(6)

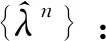
(7)

5) 重复步骤2)～步骤4)，对于给定判别精度e>0，若

(8)

则停止迭代。最终，得到具有AM-FM信号特征的K个IMF分量信号。

1.2 广义S变换原理

设h(t)为平方可积的函数，则可以定义h(t)的S变换为：

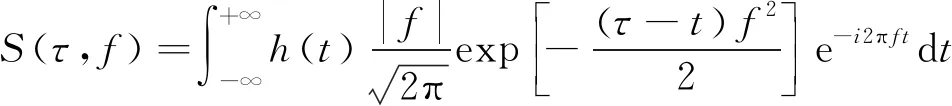
(9)

式中：τ为时间；f为频率；S(τ,f)为h(t)的S变换。

其中,S变换的基本小波函数定义为：

gf(t)exp(-i2πft)

(10)

式中：gf(t)为高斯窗函数，可定义为：

(11)

由于S变换的基本小波窗函数形态固定，使其不能够依据实际情况来调整窗口的大小，在高频部分分辨率低，导致在实际应用中不能得到较好的效果。

广义S变换是在S变换上的改进算法，对于S变换现在已经有多种改进方法，本文采用陈学华提出的二参数广义S变换法[19]，通过加入两个参数rgs和ρ来调节高斯窗函数(式(11))的大小，见式(12)。

(12)

从而得到信号h(t)的二参数广义S变换为

(13)

通过调整rgs和ρ，就可以获得高的时频分辨率。

1.3 衰减梯度求取

“低频伴影”技术已经成为含气性检测一种常用方法，它主要依据当遇到油气时“低频能量增强，高频能量减弱”的特性。其需要对不同频段的剖面进行对比，且需要注意频率的选取范围。衰减梯度已经成为油气检测的一个重要属性,衰减梯度主要依据在含气目的层高频能量快速衰减的原理，其仅需一个剖面即可反映我们所需信息，且不需人为寻找频段。衰减梯度值大的地方往往表示此处存在强振幅异常，高频衰减较快，排除其他因素影响一般表现为含油气反应。衰减梯度的提取离不开时频分析方法，笔者采用具有高时频精度的广义S变换来进行衰减梯度的提取。

衰减梯度通常采用EAA方法求取，根据粘弹性理论，依据均匀不完全弹性介质产生的吸收效应,使地震波振幅随地震波传播距离的增加呈指数衰减的特性，拟合出频谱中高频衰减异常部分，这里我们使用广义S变换来获得相应的频谱信息，即对于地震信号h(t)的广义S变换时频分布Xω(τ，f)，它与衰减梯度a的拟合关系可以表示为:

Xω(τ,f)=ce-af

(14)

式中的c为常数,然后对式(14)中两侧分别取对数：

ln[Xω(τ,f)]=lnc-af

(15)

然后，通过计算总能量85%与65%对应的位置频率与所对应的地震波能量，通过拟合斜率，对式(15)进行变换，可得式(16)。

(16)

EAA方法示意图见图1。

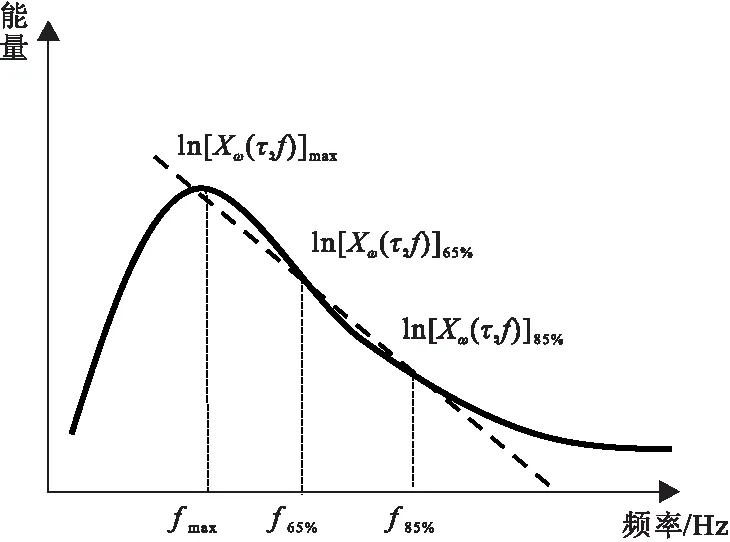
图1 EAA方法原理Fig.1 EAA schematic

应用VMD结合广义S变换提取衰减梯度的方法步骤：

1) 对地震数据剖面进行VMD分解。对分解后的模态函数进行相关性计算，从相关系数中选取具有强相关性的分量作为特征分量，将选取的特征分量合成重构地震剖面。

2) 衰减梯度提取。传统的EAA技术只适用于高信噪比的平滑频谱，利用VMD分解后，获得高信噪比的信号，再对重构后的地震剖面逐道进行二参数广义S变换，利用最小二乘法来拟合求取频谱斜率，并将其作为该时间点的衰减梯度值，逐道逐点计算衰减梯度值，最终得到整个衰减梯度剖面。

3)通过衰减梯度剖面，结合实际工区已知的相关资料，对含气储层进行分析。

具体流程如图2所示。

图2 VMD与广义S变换提取衰减梯度流程Fig.2 Schematic diagram of VMD and generalized S transform extraction attenuation gradient

需要值得注意的是VMD分解的参数对结果影响较大,K值过大会导致分解过度，产生虚假分量；K值过小，则不利于各模态分量的中心频率的捕获。K值过大或过小都会直接影响到结果的准确性，在多次试验中发现，K值一般取值在3～5之间时较为合适。

2 模型测试

为验证VMD的优越性，我们用主频分别为30 Hz、45 Hz和50 Hz的单频信号y1、y2、y3合成信号y分别进行CEEMD分解和VMD分解进行比较。其中分量信号表达式为y1=sin(2π*30t),t∈[0,1000](图3(a));y2=cos(2π*45t),t∈[600,1000](图3(b));y3=sin(2π*50t+15π),t∈[0,400](图3(c))；y(图3(e))是将y1、y2、y3叠加后再加入白噪声(图3(d))后的合成信号。

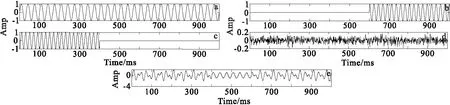
图3 合成信号及分量信号Fig.3 Synthesized signal and component signal(a)分量信号y1;(b)分量信号y2;(c)分量信号y3;(d)噪声信号;(e)合成信号y

为了展示VMD分解方法的优势，对图3中合成信号y进行分解。图4为CEEMD分解后得到的模态分量及其对应的振幅谱。由图4发现，CEEMD分解中IMF1分量主要为高频噪声分量；IMF3为30 Hz分量，出现轻微模态混叠现象； IMF2与IMF4出现了严重的模态混叠现象，这主要是因为IMF1分解不完全，及残留噪声等因素影响，通过递归传递向下传递分解所导致的。

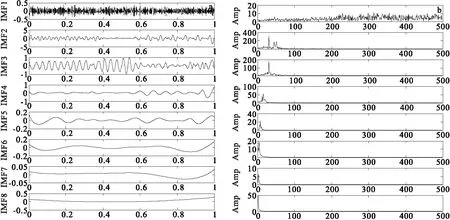
图4 CEEMD分解模态分量及其振幅谱Fig.4 CEEMD decomposed modal components and the amplitude spectrum(a)分解模态分量;(b)分解振幅谱

图5为VMD分解的分量及其对应的振幅谱。由图5中，可以清楚地看到，合成信号经过VMD分解后，完美的将30 Hz、45 Hz、50 Hz三个不同频率成分的分量信号分解了出来，在IMF4中主要为添加的噪声信号，有效克服了模态混叠问题，体现了VMD的优越性。这是由于VMD的非递归分解完全改变了以往的递归模态分解，且有着坚实的数学基础做约束，从而其分解分量都为窄带信号且约束在其中心频率附近。与CEEMD分解得到的8个IMF分量相比，VMD只需分解4个分量就可以分解出每个子信号，分解后的模态分量更加精确,且VMD可以有效对噪声信号进行分离，这也是很多研究者选择使用VMD去噪的原因之一。

图5 VMD分解模态分量及其振幅谱Fig.5 VMD decomposition mode components and the amplitude spectrum(a)分解模态分量;(b)振幅谱

3 实际工区应用

本文所用数据为南海某实际工区的叠后地震数据中截取的一个连井剖面如图6(a)，截取时间为2.4 s～2.85 s，受采集方式和外界其他因素等影响，储层较周边反射层响应较弱。其中包含了井1、井2和井3三口井，测井曲线为密度曲线，结合测井曲线与已知相关资料，得知井1为高产井，井2为含水气井(含气量少)，井3为弱含气井，笔者主要对高产井井1含气性进行研究。由实际工区资料及测井解释结果得知井1中包含油气层分别位于如图所指位置(图6(b))。

图6 实际工区Fig.6 Orignal seismic section(a)实际工区连井剖面；(b)井1放大剖面

首先对井1的井旁地震道作VMD分解见图7，其中参数为K=3。并将各分量与原始地震道进行相关性计算(表1)，从表1中可以得到IMF2相关系数最大，表现为强相关。对原始地震剖面进行VMD，得到IMF1～IMF3三个分量剖面(图8(a))。从图8中可以看到，相对于原始剖面，IMF2剖面很好的包含了主要目的层信息。原始剖面目的反射层能量受岩性等其他因素影响显示较弱，IMF2剖面对目的层的反射明显得到了增强，且经过VMD分解后的信号为窄带信号，具有更高信噪比与频谱更加平稳的优点，更有利于后期对衰减梯度的提取。因此选取IMF2剖面作为后期研究的特征剖面。

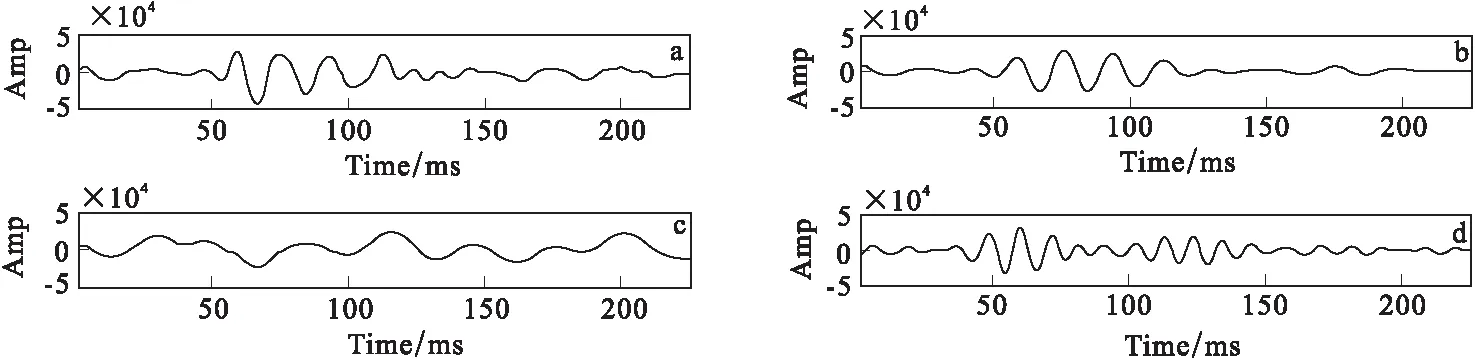
图7 井1井旁地震道及其VMD分解分量Fig.7 Seismic track beside well 1(a)原始信号；(b)IMF1；(c)IMF2;(d)IMF3

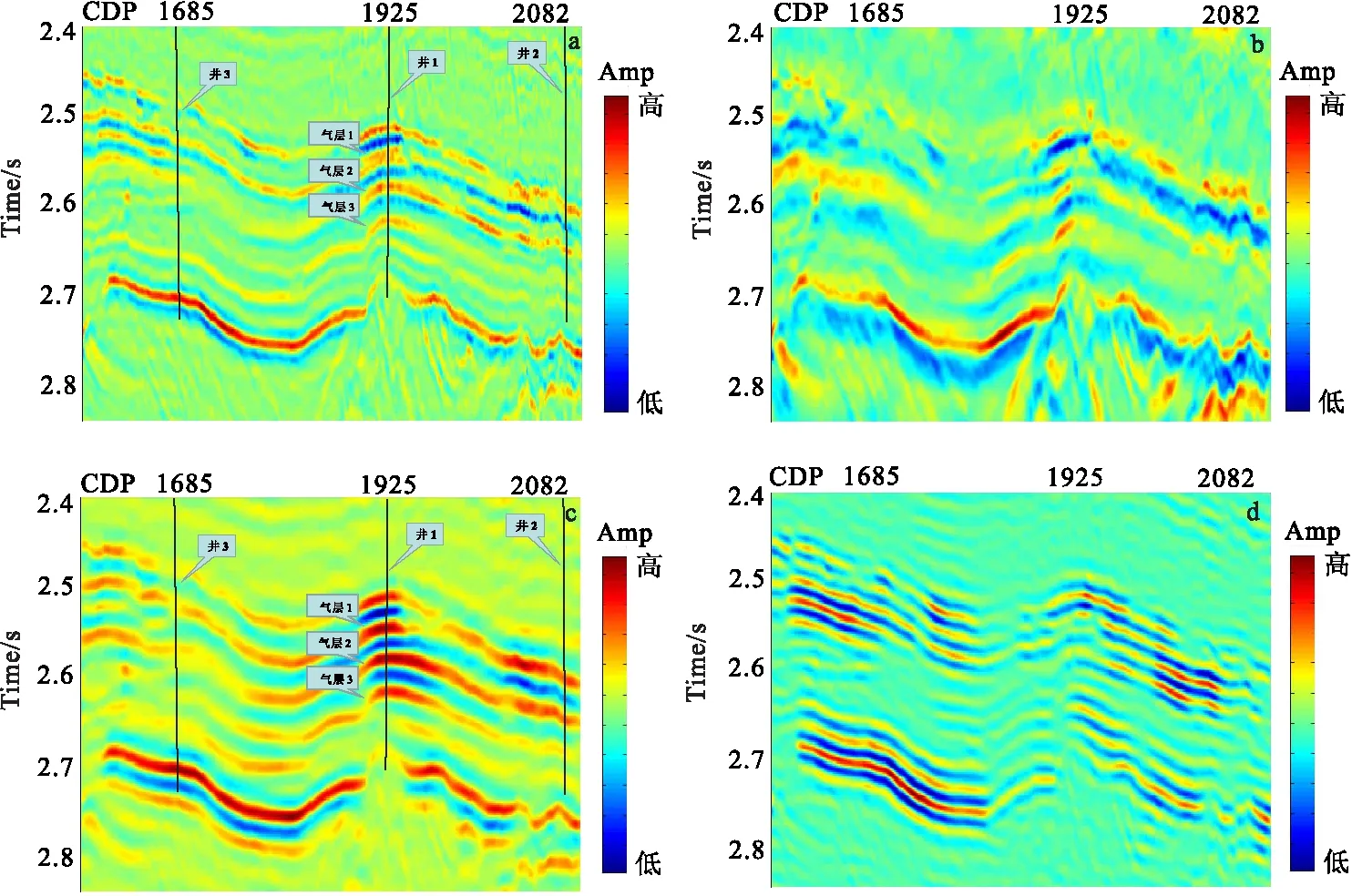
图8 原始剖面及VMD分解剖面Fig.8 Original section and VMD decomposition section(a)原始剖面;(b)IMF1剖面;(c)IMF2剖面;(d)IMF3剖面

表1 井1井旁地震道与其各IMF分量的相关系数

为突出本文方法的可行性与有效性，首先对图8(a)进行分频处理，并利用“低频伴影”的方法来进行含气性的检测，所得结果如图9所示。从图9中可以看到，通过分频得到了两个不同频段的分频剖面，在高频段(图9(b))中含油气层比低频段(图9(a))的能量有所减弱，表现出“低频伴影”效应。但从图9中可以观察到分频剖面分辨率低，无法准确指示出目的层，且需要对两图进行比较才可以得出结论。

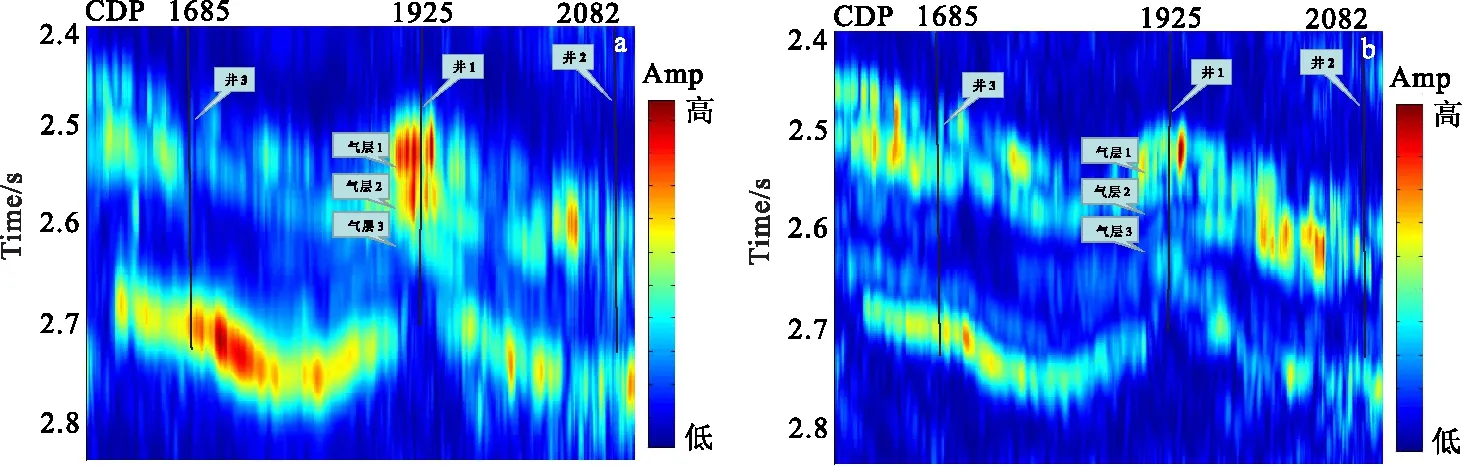
图9 分频剖面Fig.9 Frequency-division section(a)10 Hz～20 Hz分频剖面; (b)20 Hz～30 Hz分频剖面

图10为应用不同方法提取的衰减梯度剖面。由图10观察到，传统基于原始剖面直接使用广义S变换提取的衰减梯度(图10(a))，目的层能量较弱，反应不明显。笔者经VMD处理后再使用广义S变换获得的梯度剖面，衰减梯度强能量明显，分辨率高。对于强含气井井1，经这里VMD结合广义S变换获得的衰减梯度剖面(图10(b))，在目标区域位置都表现了强衰减梯度反映，表明此处存在振幅异常和频率异常特征，可能为含油气储层。对比上述所选用的分频方法，本文方法仅需一个剖面即可，更为直观，分辨率更高。为进一步确定本文方法有效性，将图10(b)中井1旁的衰减梯度剖面进行放大，并加入测井曲线(所选测井为密度曲线)，见图11。依据密度曲线含油气性处通常显示为低值的特性与已知实际工区资料结合，从图11可以看到，使用本文方法所得衰减梯度剖面很好地吻合了含油气部位。综上所述，证实了本文方法对研究工区储层含油气分布分析的可行性与有效性。

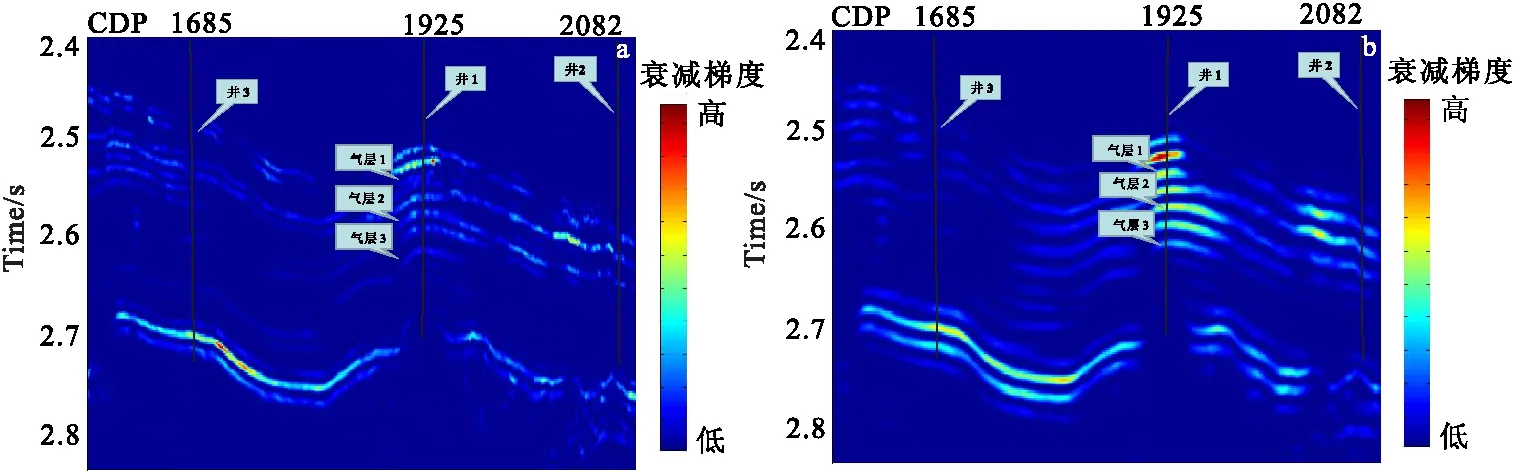
图10 不同方法得到的衰减梯度剖面Fig.10 Attenuation gradient profiles obtained by different methods(a)仅使用广义S变换的方法;(b)本文方法

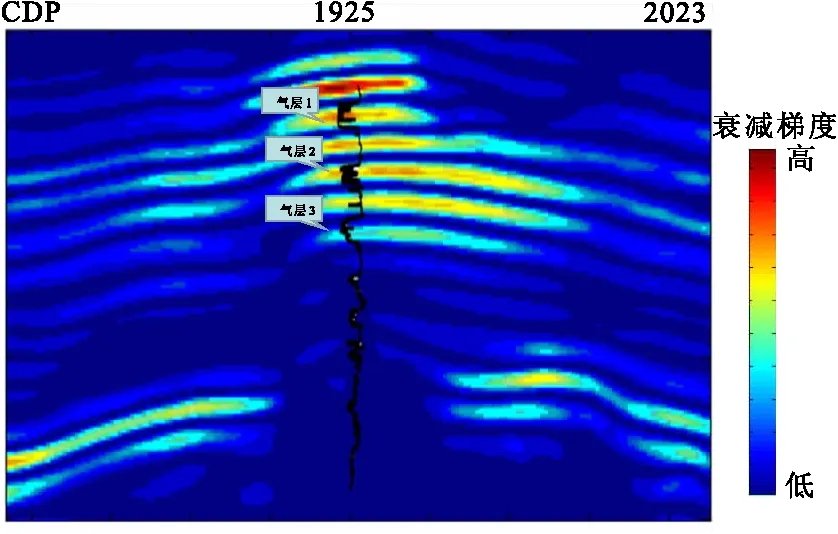
图11 井1衰减梯度剖面Fig.11 Well 1 attenuation gradient profil

4 结论

由于海上数据采集中受采集方式等多方面干扰，造成工区数据中含油气反射层信息较弱，笔者将VMD结合二参数广义S变换，通过VMD分解维纳滤波的特性和自身分解方式的优势降低了噪声的干扰，并加强了地震信号中弱含气信号的响应特征。然后，通过二参数广义S变换的灵活性和对时频分辨能力的适应性，使得在高频段得以提取更精准的衰减梯度，从而获得更高的分辨力。使用本文方法,可以直观精确刻画宽带地震数据中的特定频带含气储层的强振幅能量异常与高频的快速衰减。通过对实际工区的应用处理，进一步证明了本文方法在含油气性检测中的有效性和优越性。