用给定转角分步实现刚体任意有限转动的研究
巩浩然 武 迪 龚胜平 李俊峰
∗(清华大学航天航空学院,北京100084)
†(北京航空航天大学宇航学院,北京100191)
1775年,Euler[1]使用球面几何方法首次证明了任意有限刚体旋转运动都可以等价为一次绕某固定转轴的定轴转动。同时欧拉创造性地提出了欧拉角的概念,即刚体的任意姿态运动,都可以分解为3次绕固连系坐标轴的定轴旋转之叠加(连续两次的转轴不可相同),经典的分解顺序包括依次绕z-x-z轴旋转的进动、章动、自转,和依次绕z-y-x轴旋转的偏航、俯仰、滚转等。这种分解方法清晰易懂、方便可视化,尤其为工程应用带来了诸多便利。1973年,NASA研究人员Davenport[2]在欧拉角正交分解的基础上,研究了将刚体转动分解为几次绕非正交轴旋转的可行性及分解方法。2003年,Wittenburg等[3]进一步将问题拓展到一般的螺旋位移运动分解。
这几种姿态运动的分解虽有不同,但基本出发点一致:已知刚体某有限转动并给定几根转动轴(正交或非正交的),将该有限转动分解为绕这几根给定轴的转动之叠加。与上述研究的问题不同,本文研究的问题则是:已知刚体某有限转动,给定旋转角度大小,问该转动是否可以分解为一系列转角为给定角度的定轴运动(转轴的方向自由选取)之叠加。为了使问题阐述得更清楚形象,用三维欧式空间中的质点位移做个类比。上述已有的研究类似于已知质点某有限位移,给定几个空间方向(正交或非正交),将该有限位移分解为沿这几个给定方向的位移之和。而本文的研究问题则类似于,已知质点某有限位移,给定单步运动步长,是否可以将该有限位移分解为一系列步长为给定步长的位移运动之叠加。
举例来说,假设刚体需要绕z轴转动10°,如限定单次转角只能为5°,则可以拆分为2次绕z轴的旋转之和,如限定单次转角只能为2°,则可以拆分为5次绕z轴的旋转之和,如限定单次转角为3°,那么几次绕z轴的转动就无法实现需求,这时还需要去寻找z轴之外的其他转轴,将目标转动拆分为几次转角为3°的转动之和。
本问题属于较为经典的姿态运动学问题,既有其力学理论价值,也有工程实践意义。例如在依靠步进电机旋转的机构中,步进电机的转轴方向可以任意变化,但步进电机的最小步长有限制,对于某些微型步进电机,最小单步步长可以达到18°,此时依靠步进电机的姿态运动就不得不考虑本文研究的问题。此外,本文作者也在做空间多体系统通过关节运动实现姿态机动的研究,在这类问题中,有些情形下多体系统姿态运动的转角是一定的,而转轴方向的选取则有较大自由,本文所研究的问题也与之密切相关。
如图1所示的多体结构太阳帆,其姿态固连系建立在中心十字架上,1和3号帆可以绕x轴同步旋转,2和4号帆可以绕y轴同步旋转。整个帆可以看做一个由中心十字支架、1和3号帆、2和4号帆组成的3刚体系统,通过帆面的旋转,可以实现中心十字支撑(即姿态固连系)的姿态变化。当1和3号帆位于Oxy平面上时,2和4号帆的旋转会引起整星姿态(即固连在中心十字支撑上的固连系姿态)绕y轴反转,而当1和3号帆与Oxy平面形成一个夹角θ1时,2和4号帆的旋转也会引起整星姿态变化,但由于失去了对称性,此时整星转轴不再是y轴,而是偏离y轴的α轴。考虑如下一组转动:初始时刻4片帆面全部位于Oxy平面内,首先,1和3号帆旋转θ1后保持不动,接着,2和4号帆旋转nπ后保持不动(此时2和4号帆仍位于Oxy平面内),最后1和3号帆反转θ1回归原位。经历了这样一组转动后,太阳帆的构型与初始时一致,但整星姿态发生了变化,其姿态变化四元数可以由3次转动叠加得到

图1 由4片直角三角形帆面及相应支撑杆构成的太阳帆

其中,°表示四元数相乘运算。a是第一次转动后,整星绕x轴反转的角度,与θ1成正比,b是第二次转动后,整星绕α轴转动的角度,与nπ成正比,c是α轴抬离Oxy平面的角度,也是θ1的函数。固定b,而令a变化,式(1)显示,整星姿态变化的转角是一定的,而转轴的方向可以是Oyz平面内的任意方向(通过选取恰当的a)。试图通过一系列这样的3步组合转动实现太阳帆的任意姿态机动,这就不可避免地要回答一个问题:在多步姿态转动中,转角固定,而转动方向可在一定范围内选取,能否拼出任意想要的姿态变换?在这个太阳帆的问题中,转轴的方向被限定在了Oyz平面内,使得问题更加复杂,这里先来看看转轴方向可以任意选取时的情况。
在下一节中,使用姿态四元数作为主要工具,通过构造性的证明方式,证明上述分解的可行性,并给出分解方法。
1 问题描述及证明
1.1 问题的数学描述
对于某一转轴方向为e,转角为m的给定刚体定轴转动(用姿态四元数描述)

是否可以通过一系列转角n i给定,转轴方向e(i)任意的定轴转动

拼凑而成?即是否可以通过恰当选取每次转动的转轴e(i)使得q=q(1)°q(2)°...°q(k)?
1.2 一种构造性证明
首先,上述问题的答案是肯定的,通过有限次转角依次为n1,n2,···n k的定轴转动,一定可以拼接出某一转轴方向为e,转角大小为m的定轴转动,且一定可以在k次内完成,这里k表示满足的最小整数。具体分解方法如下:
(1)当m≥n1+n2时,取转轴方向e(1)=e,靠近目标姿态,设在第i−1步后,距离目标姿态的一次转动转角为m i-1,如m i-1≥n i+n i+1,继续取转轴方向e(i)=e;如m i-1 (2)当m 不失一般性地,可以假设目标转动q的转轴e=[0,0,1]T,因为对于任意转动,总能找到一个旋转坐标系,使得在该坐标系下,转轴方向为[0,0,1]T。令两次转动之叠加等于目标转动 注意,这里e1,e2并非在同一坐标系下的两个方向,e1是在空间惯性坐标系下的方向投影,e2则是基于e1转动之后的刚体固连系上的方向投影。方程(4)可展开为 因为单位四元数模为1的天然约束,如式(5)所示的4个标量方程中,只有3个独立方程,而独立未知量则有4个(每个转轴方向含2个独立未知量),故方程(4)的解并不唯一。设 代入方程(5)整理可得四个解 上述4个未知量的解只有3个是独立的,方便起见,取式(7)~式(9)为一组解,观察该解,式(8)和式(9)说明e1,e2在z方向的分量可以确定,式(7)说明e1,e2两方向的夹角可以确定,满足式(7)~式(9)均为可行解。解存在的条件为 与情况(2)的条件相符。 设目标刚体姿态运动为绕初始z轴旋转2π/3,依靠步进电机实现该运动,假设该步进电机的转轴方向可以任意取定,最小单步转角为π/5。根据上一节的讨论,由于2π/3>π/5+π/5,首先令步进电机转轴方向取为z轴,经1次转动后距离目标姿态2π/3−π/5=7π/15,因为7π/15>π/5+π/5,继续令步进电机转轴方向为z轴,经第2次转动后距离目标姿态7π/15−π/5=4π/15。此时因4π/15<π/5+π/5,将m=4π/15,n i=π/5代入方程(7)~方程(9)可得 满足式(12)的解均为可行解,不妨取两次转动的四元数为 综上,步进电机的4次定步长转动,即可实现目标姿态运动,图2为第3和第4两步旋转分解的示意图。初始姿态固连坐标系(经过前2步转动后的刚体固连坐标系)Ox0y0z0,目标姿态固连坐标系Oxfyfzf,经过前3次旋转后的刚体固连坐标系Ox1y1z1。为了展示清晰,除坐标系外,还画出了一个假想的手机状刚体。图中e1,e2为第3和第4两次旋转的旋转轴(均已转换到第2次旋转后的刚体固连坐标系下)。 图2 实验案例中的旋转分解示意图 关于姿态运动分解的过往研究,多集中于给定“基方向”,如何选择适当的转角以实现任意姿态变换;本文则是给定旋转步长,自行寻找适合的“方向”以实现任意姿态变换。本文通过四元数运算证明,通过有限次旋转步长给定、旋转轴方向任选的定轴旋转,可以实现任意的刚体空间旋转。这种分解的可行性将为姿态运动学的理论分析和实践运用带来一些新思路。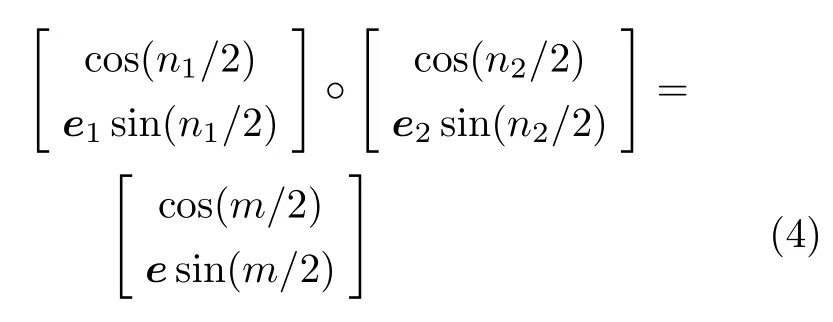
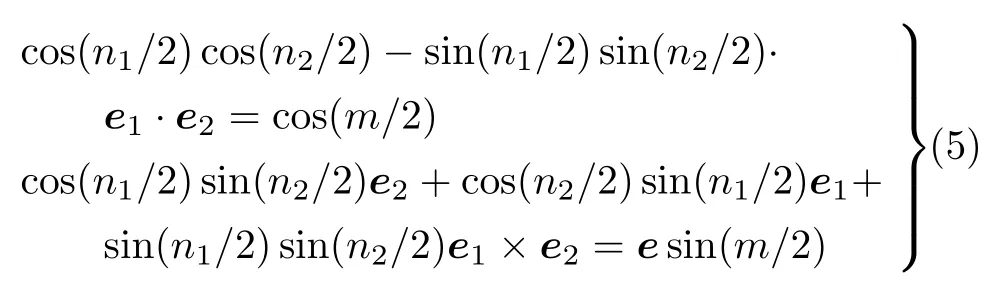

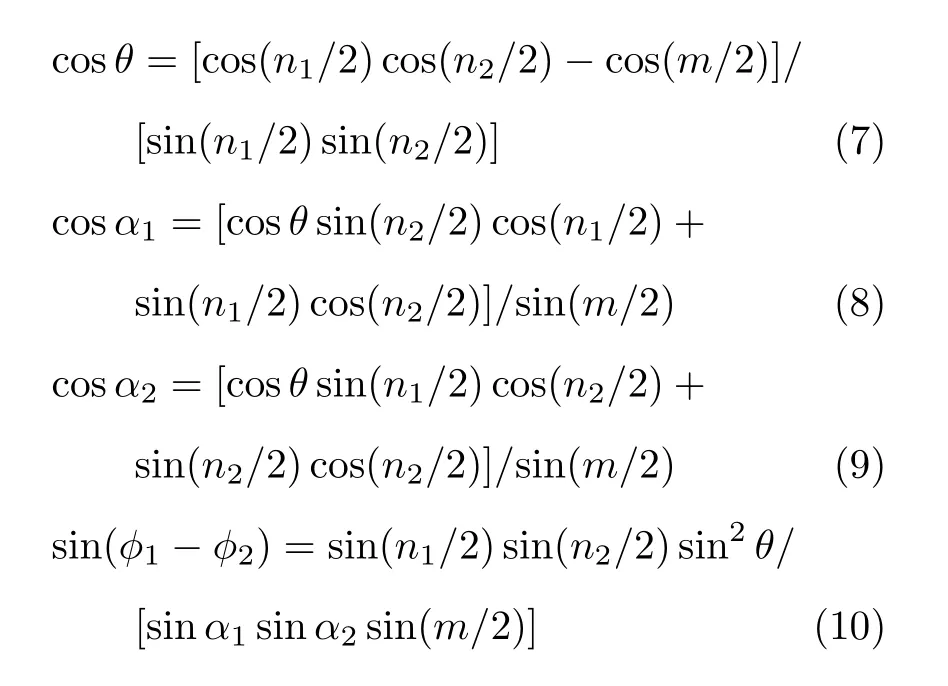
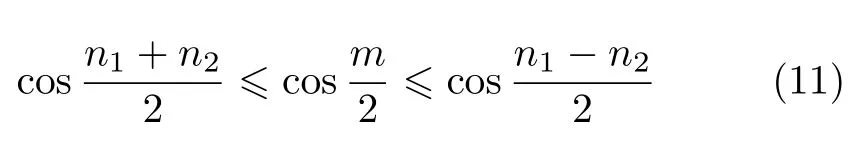
2 例子



3 结论

