磁浮车桥耦合振动性能模拟的离线混合试验方法

国 巍， 龙 岩， 邵 平， 曾 晨， 喻泽红

(1.中南大学土木工程学院， 长沙 410000； 2.高速铁路建造技术国家工程实验室， 长沙 410000)

磁浮轨道交通作为一种新兴的交通方式，车桥耦合振动问题突出. 在高速运动下，令仅有10 mm磁浮间隙的上部列车保持稳态悬浮需要良好的控制系统，若车桥耦合产生强烈振动，磁浮控制可能会失效进而导致事故发生，因此控制系统是需要进行测试的重要环节[1-2]. 在理论研究的基础上，需在现场和实验室进行大量测试，以检验磁浮控制、车桥耦合振动等性能. 现场测试需耗费大量财力，组织难度大，在无法保证桥梁结构、控制系统等可靠性时进行现场实测会造成人财浪费甚至危险，因此有必要发展实验室内的测试方法.

混合试验技术近年来被认为是可实现桥上行车测试的手段之一[3]，已应用于实验室内高速铁路桥上行车相关试验测试，采用实时混合试验以准确模拟桥上行车状态. 此外，实时混合试验也被广泛应用在土木工程中其他领域，如Jiang等[4]对物理磁流变阻尼器及数值公路桥梁进行实时混合试验测试，验证了磁流变阻尼器控制公路桥梁疲劳振动的有效性；Friedman等[5]在装有磁流变阻尼器的大型框架中进行了实时混合试验；Najafi等[6]提出一种基于模型的轻阻尼和高非线性结构系统实时混合试验方法，其用于屋顶轨道非线性能量吸收器性能研究. 实时混合试验具有较高的实时性要求，大型伺服液压系统作为混合试验中车辆等物理子系统的执行机构，需要高精度控制系统，同时大型复杂结构的计算也要求在毫秒内完成，具有很高挑战. 相比于实时混合试验，学者们提出了离线迭代的混合试验新思路，并应用于汽车轮胎耐久性测试、非结构构件等试验中，如Maddaloni等[7]提出基于传递函数的开环补偿模型，对安装吊顶的框架顶部x、y和z向进行离线迭代补偿；Zhou[8]等提出一种多自由度离线耦合迭代法用于非结构系统振动台试验中楼面响应谱的再现；MTS公司提出一种混合系统响应收敛方法，利用混合试验对汽车轮胎进行了疲劳和耐久性测试[9]；Li等[10]采用离线耦合试验方法应用于偏置电力变压器性能评估. 非结构构件往往是大型建筑或汽车系统中的设备与部件，从构成来看其类似于桥上行驶的车辆，区别在于桥上行车为移动设备，非结构构件往往为固定设备.

基于实时混合试验所存在的问题，本文发展了一种基于不动点迭代算法的离线迭代混合试验方法，其可以避免实时计算难题，同时可以在实验室内进行磁浮车桥耦合振动性能的模拟.

1 基于不动点迭代的离线混合试验方法

与实时混合试验在每一时间步内实时模拟桥上行车状态相比，离线混合试验通过在数值物理子系统间迭代修正力或位移时程响应误差，令其在边界处平衡协调，进而模拟桥上行车真实状态. 本文在离线混合试验中用于迭代修正响应误差的方法为不动点迭代算法. 基于不动点迭代的离线混合试验方法是在振动台系统包含的内环控制器[11]基础上，搭建外环控制器，原理如图1所示.

图1中，外环输入是z方向的系统初始位移时程，u为外环不动点迭代控制器输入给内环控制器的位移命令，ut为振动试验台自身所带内环控制器以u为期望响应经迭代修正后复现的位移响应，即内环控制器下达至振动台的控制命令，u′为数值- 物理划分界面处的位移响应，即振动台台面位移，F为磁浮车辆模型在振动台激励下反馈的磁浮力.

磁浮车桥离线迭代混合试验系统将数值- 物理切分界面选定为车辆与轨道梁之间，磁浮车辆作为物理子系统，磁浮轨道桥梁作为数值子系统，子系统间以参照实际行车，以磁浮力的大小与其在轨道梁作用点处所受力的大小相等作为边界条件，即2个子系统通过磁浮力连接.因磁浮列车与轨道间的力作用关系不同于传统的轮轨接触，且数值- 物理子系统切断了实际磁浮车桥系统间力磁浮力的传递，因此将车辆子系统反馈回来的磁浮力以移动荷载的形式加载至数值桥梁子系统.内环控制器用于实现振动试验台对于其输入信号的高精度复现；外环控制器通过不动点迭代收敛算法[12]，逐步减小混合试验中数值桥梁子系统与物理车辆子系统之间的动态响应误差，从而在数值- 物理划分界面处实现一定精度的磁浮车桥耦合振动复现.

实验室内的混合试验依托于振动试验台系统，因其自带的液压系统控制器可高精度复现输入至振动台的期望信号，故在模拟磁浮车桥耦合振动时忽略振动台复现误差，即仅对磁浮车桥系统间响应误差进行迭代修正.在磁浮桥上行车试验中，因子系统间以磁浮力协调为边界条件，因此在进行收敛判别时选择车辆位移与磁浮力作用点处轨道梁的位移响应，当两者间计算的均方根误差小于限值时，则认为离线混合试验收敛，即可在一定精度上复现磁浮车桥动态耦合.外环不动点迭代控制器的原理如图2所示.

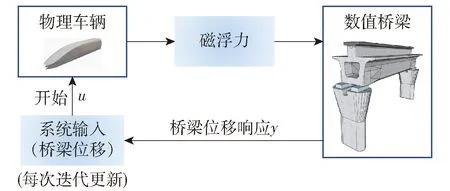
图2 不动点迭代算法流程Fig.2 Flow of fixed-point iterative algorithm

若基于磁浮车桥耦合的离线迭代混合试验系统的输入为作用于车辆模型的桥梁位移激励u，输出为车辆模型在激励输入下生成的磁浮力作用于数值桥梁模型后的桥梁位移响应y，对于此离线混合系统，其输入输出间的关系可由y=H(u)表示，则离线迭代混合试验的目标可表示为

error=u-y=u-H(u)=0

(1)

离线混合试验的目标可以转换为求解式(1)的解，且存在唯一解u.将式(1)化为同解方程可得

u=H(u)

(2)

取任意初值u0带入式(2)右侧

u1=H(u0)

通过迭代可得

u2=H(u1)
⋮
uk+1=H(uk)k=0,1,2,…

(3)

式中：uk为第k步迭代序列，式(3)为求解式(2)的不动点迭代法.若存在一序列u*，使迭代序列uk满足

(4)

则称不动点迭代法收敛，u*为式(2)的解，否则称为发散.

将上述不动点迭代法应用到磁浮车桥系统的响应收敛中，流程如图3所示.

图3 基于不动点迭代的离线混合试验操作流程Fig.3 Operation flow of off-line hybrid test based on fixed point iteration

1) 将一组初始位移驱动信号u0输入至振动台，振动台以初始驱动位移信号为目标进行内环控制并加载至磁浮车辆，加载完成后，记录反馈力.

2) 将反馈力作用于桥梁数值模型，计算得到位移响应并换算为振动台台面位移信号.

3) 比较换算后振动台台面位移输出时程和驱动位移信号，若计算均方根误差小于限值，则离线混合试验收敛，试验结束；反之，则令换算后的振动台台面位移信号作为下一步驱动位移信号.

4) 循环执行步骤1)～3)，直至驱动位移信号收敛，结束试验.

5) 以收敛的试验工况为准给出最终的试验测试结果.

步骤3)中所述均方根误差(root mean squared error, RMSE)通过桥梁响应相对系统输入的偏离程度判断迭代效果，具体计算公式为

(5)

式中：yk(i)为第k次迭代的系统输入；xk(i)为第k次迭代的系统输出响应.

不动点迭代算法的核心是将本次迭代计算出的桥梁位移响应作为下一次迭代作用于车辆模型的系统输入，若二者间的均方根误差小于阈值，则结束迭代，并以收敛时试验工况的系统输入作为最终测试结果，即磁浮车桥耦合振动响应.

2 数值环境的磁浮车桥离线混合试验

2.1 数值磁浮车辆模型

以中低速磁悬浮列车为研究对象，其主要构件包括车体、空气弹簧、悬浮架、电磁铁等. 每节车由车体及5台悬浮架组成，车体与悬浮架通过4个空气弹簧装置连接，每台悬浮架有4对电磁铁. 每对电磁铁配有4个电磁铁控制线圈[13]. 图4(a)所示为中低速磁浮列车实际构造，图4(b)为其构造示意图.

图4 中低速磁浮列车Fig.4 Low speed maglev train

因本文研究重点在于验证离线迭代混合试验方法在磁浮车桥系统耦合作用中的可行性，故对磁浮列车进行了下列简化：1)整个磁浮列车简化为单个移动弹簧质量块系统模型，将磁浮车体简化为一个质量块，悬浮架(5对)简化为一个质量块，悬浮电磁铁(5×4对)简化为一个质量块；2)整车的空气弹簧及悬浮架与电磁铁间的黏弹性连接分别简化为一组单弹簧阻尼系统；3)整车的电磁悬浮力简化为单点磁浮力，电磁铁与轨道梁之间通过使用线性弹簧和阻尼器模拟电磁悬浮关系. 在该简化模型中，车体、悬浮架与电磁铁均只考虑竖向自由度，最终磁浮车辆模型简化为三自由度模型，如图5所示.

图5 简化的磁浮车辆模型Fig.5 Simplified maglev vehicle model

图5中，m2、m1、m0分别表示简化模型中车体、悬浮架和电磁铁的质量；c2、c1、c0分别为二系悬挂、一系悬挂和等效磁浮力的阻尼；k2、k1、k0分别为二系悬挂、一系悬挂和等效磁浮力的刚度；x2、x1、x0、xb分别为车体、悬浮架、电磁铁和轨道的位移响应.简化车辆模型的运动方程为

(6)

式中：Mv为车辆运动方程的质量矩阵；Cv为阻尼矩阵；Kv为刚度矩阵；Xv为车辆的位移响应矩阵；Fv为外荷载列向量，即电磁悬浮力列向量.本文磁浮列车模型的具体参数[14]如表1所示.

表1 磁浮车辆模型参数

2.2 数值磁浮桥梁模型

本文研究的磁浮桥梁类型为单向简支梁桥，其主要由桥墩、支座垫石、混凝土梁、底座、自密实混凝土层、轨道板等组成[15]，示意图如图6所示.

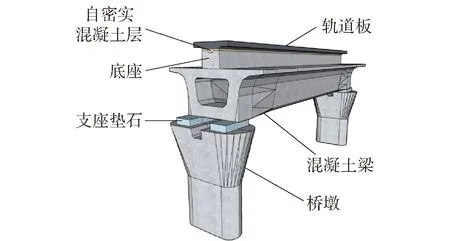
图6 磁浮桥梁模型三维图Fig.6 3D drawing of maglev bridge model

基于达朗贝尔原理可知数值磁浮桥梁的动力平衡方程为

(7)

式中：mb为磁浮桥梁的质量矩阵；cb为阻尼矩阵；kb为刚度矩阵；f为作用于桥梁的外荷载，即磁浮力.

根据阵型叠加法原理，换算整理后可得到桥梁的振动方程

(8)

表2 混凝土磁浮桥梁模型参数

2.3 离线迭代混合试验系统

磁浮桥上行车试验系统中的数值物理切分界面确定为在车辆与轨道梁之间，如图7所示，并在数值环境中进行研究和测试. 因振动台执行机构可通过内环控制实现信号的准确复现，故在搭建车桥系统时，不对振动平台进行建模.

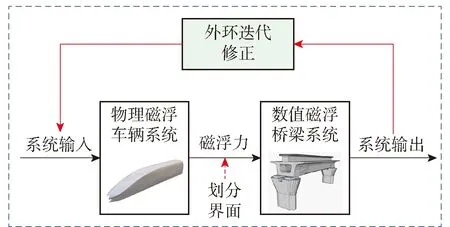
图7 离线混合试验数值- 物理系统切分界面示意图Fig.7 Sketch of interface between numerical and physicalsystem in off-line hybrid test

图8所示为磁浮车桥离线迭代混合试验系统在SIMULINK中框图[16-17]，系统输入位移信号作用于磁浮车辆模型，车辆模型在激励下生成磁浮力并作用于桥梁模型，记录桥梁竖向位移响应作为系统输出. 系统输入与系统输出通过外环不动点迭代修正二者间误差，最终实现磁浮车辆- 轨道耦合振动动态吻合.

图8 数值环境离线混合试验系统Simulink示意图Fig.8 Simulink schematic diagram of off-line hybrid test system in numerical environment

3 离线混合试验验证

3.1 磁浮桥上行车仿真计算

3.1.1 无轨道不平顺的桥上行车仿真计算

进行离线混合试验前，首先进行磁浮桥上行车的仿真计算，在不添加轨道不平顺的前提下，磁浮列车以300 km/h的速度移动过桥，计算得到磁浮轨道在荷载作用点处的竖向位移作为磁浮桥上行车的标准解，如图9所示. 图9(a)即为无轨道不平顺时磁浮桥上行车仿真计算时程结果，图9(b)为对应的桥梁竖向位移频谱，可知在不添加轨道不平顺时，磁浮桥上行车后桥梁竖向位移频率为3～5 Hz.

图9 无轨道不平顺磁浮桥上行车后桥梁竖向位移响应Fig.9 Vertical displacement response after driving on maglev bridge without irregularity

3.1.2 添加轨道不平顺的桥上行车仿真计算

实际的交通线路，如传统轮轨交通线路会因轨道初始弯曲、轨道磨耗损伤、轨枕间距不均、质量不一、路基下沉不均匀、刚度变化等因素呈现轨道随机不平顺[18]. 磁浮线路轨道不平顺与传统轮轨交通的轨道不平顺是导致车桥耦合振动的主要激振源，轨道不平顺及其他外部激励源的干扰使得磁浮列车产生振动响应，而后通过悬浮电磁铁所在转向架单元传递至下部轨道结构，最终形成车桥耦合振动效应.

在实际线路上存在的各种轨道不平顺是由不同波长、不同相位和不同幅值的随机不平顺波叠加而成的，是与线路里程有关的复杂随机过程，轨道随机不平顺的统计特征只能依靠线路实地测量获得，但工作量大不便于实施[19]. 由于缺乏磁浮线路轨道不平顺的实测数据，并没有统一的中低速磁浮轨道谱，学者[20-21]多采用高速机场谱、无缝线路轨道谱的改进形式作为磁悬浮车辆线路的随机不平顺形式，张耿等[22]利用检测到的唐山低速磁浮试验线右轨不平顺的采样数据得到了轨道不平顺谱. 中国铁道科学院拟合了统一的解析式功率谱密度函数(power spectral density，PSD)来表达轨道谱特征，即

(9)

式中：k为空间频率，单位为1/m；A～G为不平顺谱的特征参数. 本文采用的唐山中低速试验线轨道谱的特征参数如表3所示.

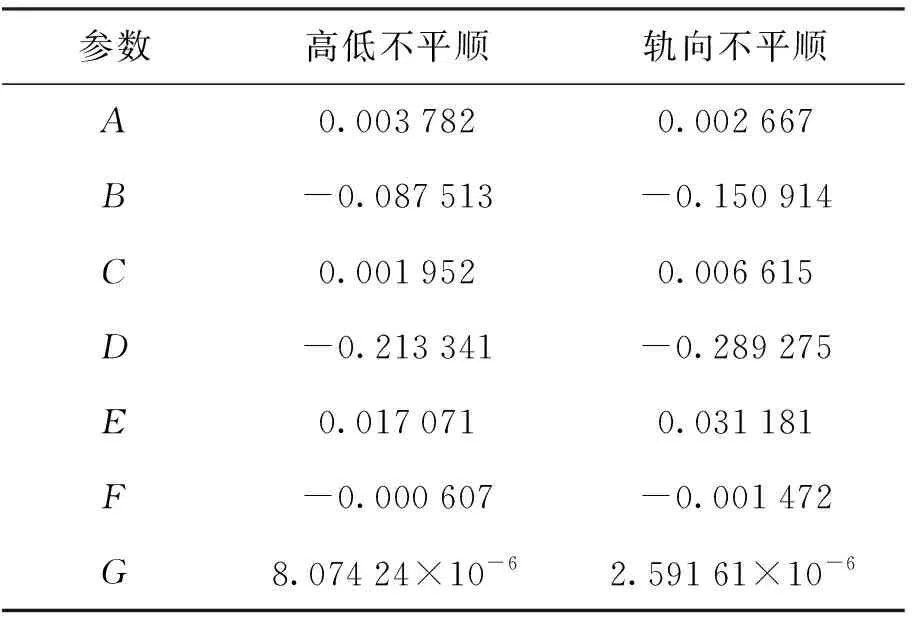
表3 磁浮轨道谱特征参数

由于轨道不平顺谱函数只适用于进行频域分析，在对系统进行时域分析时，需对轨道不平顺谱进行反演生成时域上的不平顺激励输入. 目前国内外最常用的轨道不平顺时域样本数值模拟方法有三角级数法、白噪声滤波法、二次滤波法和逆Fourier变换法(inverse fast Fourier transform，IFFT)等[23]，本文采用逆Fourier变换法进行模拟. 逆Fourier变换法由D.Cebon首次提出，是通过时间序列估计功率谱密度的Blackman Turkey周期图法，反推离散后的PDS与时间序列的关系为

(10)

式中：s(k)为离散化的功率谱密度；N为总的取样点数；D(xs)为对时间序列xs取离散Fourier变换后的复序列；X(k)为时间序列xs的Fourier频谱；X*(k)为X(k)的共轭.

式(10)直接建立了时域样本频谱与轨道不平顺功率谱密度之间的数学关系.由此可知，当已知功率谱密度时，可通过式(10)反演随机过程的Fourier频谱值，再对复序列X(k)进行Fourier逆变换，得到轨道不平顺在时域上的样本序列.

(11)

(12)

(13)

ε(k)=exp(iΦk)

(14)

式中：ε(k)为独立序列，其各分量均值为0；t为模拟时间；Φk为在[0,2π]上均匀分布的相互独立的随机变量.

根据式(11)～(14)可以计算得到功率谱函数s(k)的时域反演样本，当磁浮车辆运行速度为300 km/h、运行过带有左右各50 m过渡段的13跨32 m简支梁时，磁浮轨道竖向不平顺时域信号结果如图10所示.

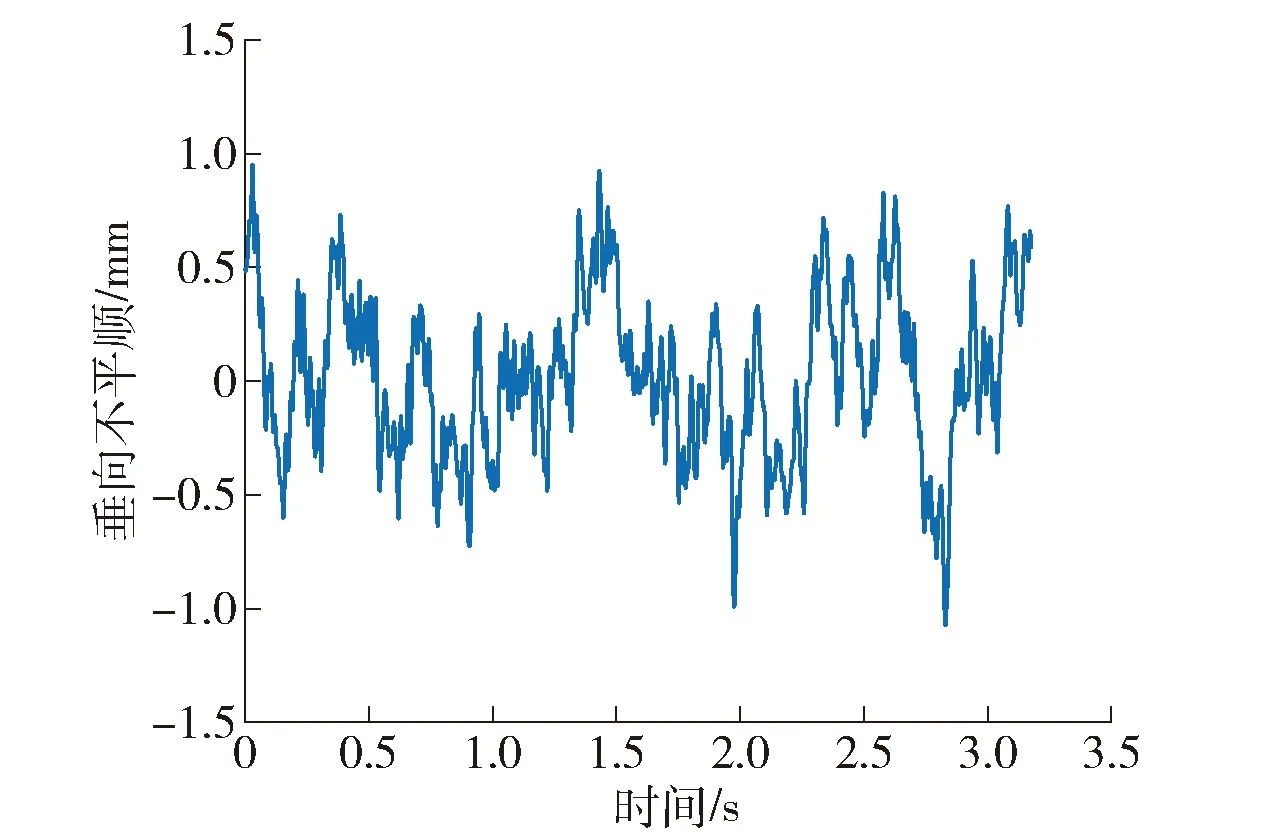
图10 磁浮竖向不平顺轨道谱反演时域信号Fig.10 Time domain signal inversion of vertical irregularity track spectrum of maglev

将逆Fourier变换法模拟出的轨道竖向不平顺时域样本序列作为磁浮桥上行车模型的竖向外部激励，计算磁浮列车以300 km/h的速度移动过桥后，磁浮轨道在荷载作用点处的竖向位移，并以此结果作为添加轨道不平顺的磁浮桥上行车标准解，如图11所示. 图11(a)为添加轨道不平顺后磁浮桥上行车仿真计算时程结果，图11(b)为对应的桥梁竖向位移频谱，可知添加轨道不平顺时，磁浮桥上行车后桥梁竖向位移频率以轨道不平顺频率为主要成分，范围为0.3～10.0 Hz.

图11 添加轨道不平顺磁浮桥上行车后桥梁竖向位移响应Fig.11 Vertical displacement response after driving on maglev bridge with irregularity

3.2 离线迭代混合试验验证

3.2.1 无轨道不平顺的离线迭代混合试验

对于无轨道不平顺的离线迭代混合试验，系统初始输入为零，但考虑到磁浮车桥模型建模时的简化处理会对结果造成一定的影响，且混合试验系统的搭建以振动台能够稳定复现为前提，未考虑振动台复现精度降低所造成的误差，故将存在的误差以随机白噪声的形式添加到系统初始输入.

将系统初始输入作用于磁浮列车模型，进行离线混合试验，记录同次迭代中的系统输入信号和桥梁响应信号，与无轨道不平顺的桥上行车仿真结果标准解进行对比，并计算桥梁响应与标准解的误差，结果如图12所示.

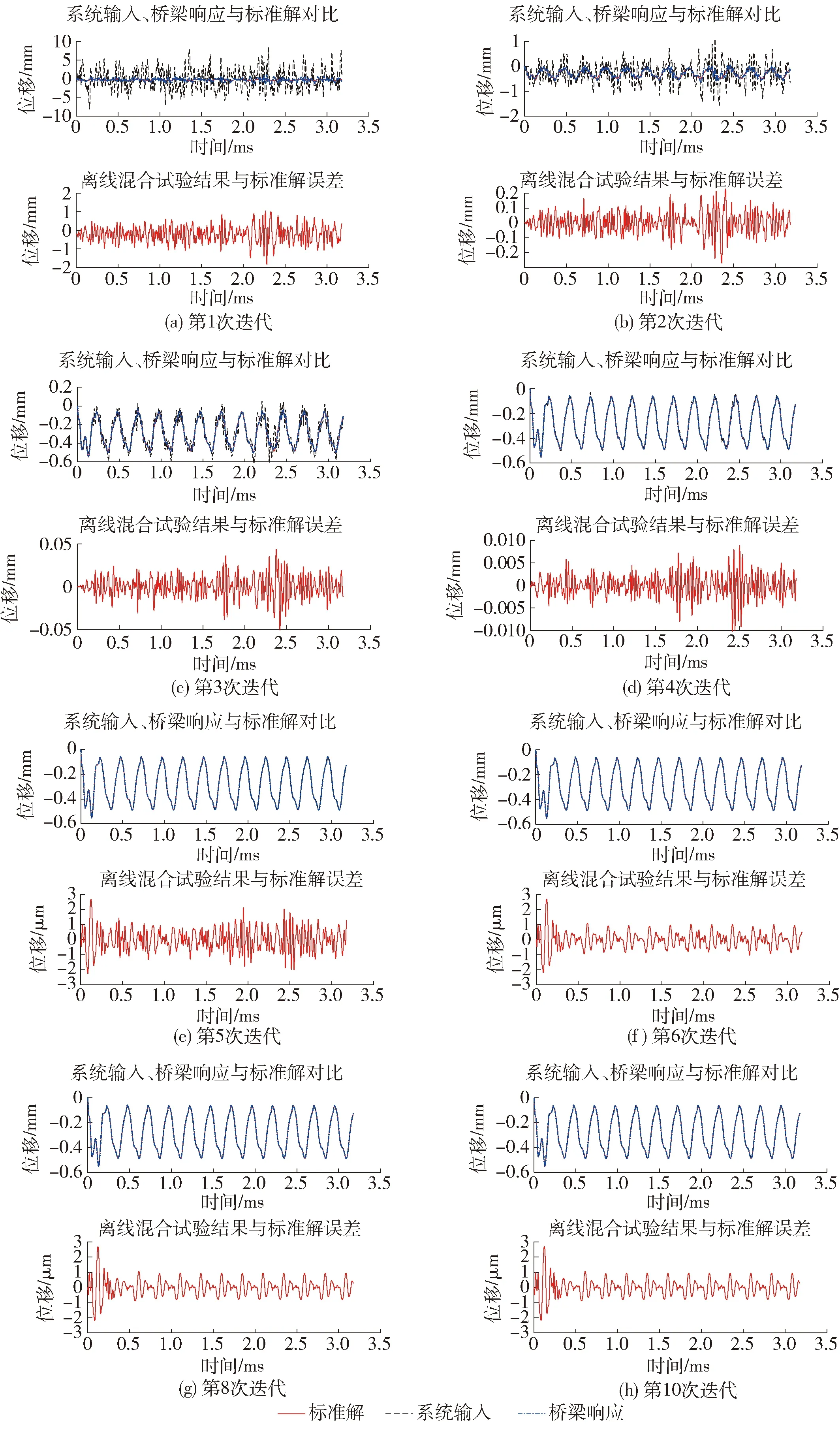
图12 无轨道不平顺离线迭代混合试验结果与标准解对比Fig.12 Comparison of off-line iterative hybrid test results without track irregularity with standard solutions

图12展示了不同迭代次数中系统输入、桥梁响应与无轨道不平顺桥上行车仿真计算结果的对比，以及桥梁响应与标准解的响应误差. 可以看出，随着迭代次数的增加，桥梁响应与标准解的波形逐渐吻合，响应误差显著下降，并基本维持在10-3毫米级.

3.2.2 添加轨道不平顺的离线迭代混合试验

首先确定试验的初始输入信号，为保证离线迭代混合试验计算结果与上文磁浮桥上行车仿真计算结果具有对比性，将系统初始输入信号选定为上文反演计算得到的磁浮轨道竖向不平顺时程. 同样考虑简化模型及振动台复现精度所带来的误差，对轨道不平顺时程添加低幅宽频白噪声以模拟该影响.

将系统初始输入作用于磁浮列车模型，进行离线混合试验，记录同次迭代中的系统输入信号和桥梁响应信号，与添加轨道不平顺的桥上行车仿真结果标准解进行对比，并计算桥梁响应与标准解的误差，结果如图13所示.

图13 添加轨道不平顺离线迭代混合试验结果与标准解对比Fig.13 Comparison of off-line iterative hybrid test results with standard solutions for adding track irregularity

图13展示了不同迭代次数中系统输入、桥梁响应与添加轨道不平顺桥上行车仿真计算结果的对比，以及桥梁响应与标准解的响应误差. 可以看出，即使系统初始输入有白噪声的影响，在迭代3次后，桥梁响应与添加轨道不平顺的桥上行车仿真结果之间的响应误差明显下降，并基本保持在10-2毫米级. 为更好地说明离线迭代混合试验方法的收敛效果，计算不添加轨道不平顺和添加轨道不平顺时每次迭代结果的RMSE，结果如图14所示.

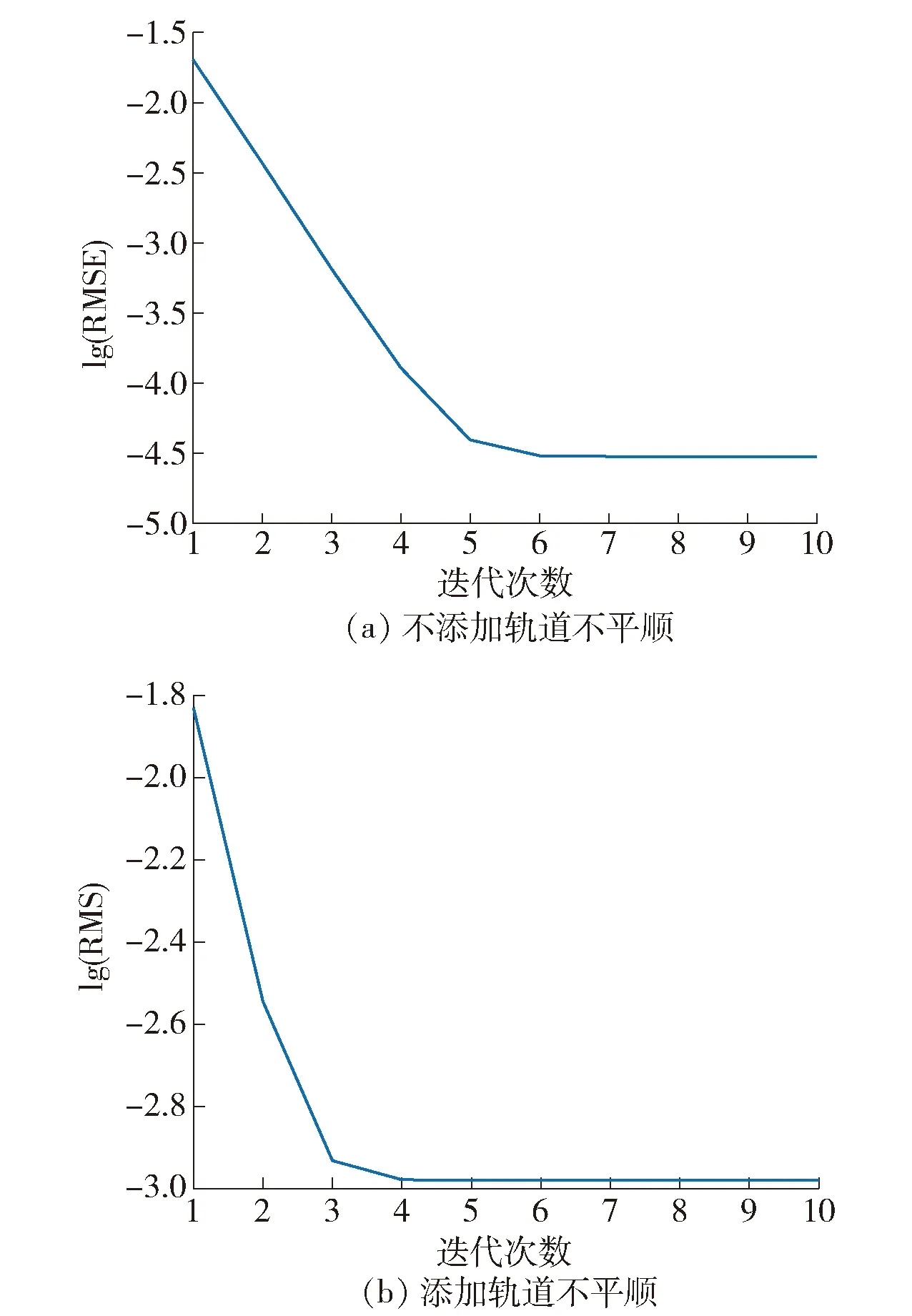
图14 前10次迭代离线迭代混合试验结果与仿真结果的RMSEFig.14 RMSE of the first 10 iterations of off-line iterativehybrid test results and simulation results

对比有无轨道不平顺工况下前10次迭代的RMSE结果可以进一步得出，随着迭代次数的增加，离线迭代混合试验结果与桥上行车仿真计算结果间的相对误差逐渐减小. 对于无轨道不平顺工况，迭代6次后，误差对数值下降到-4.5并基本保持不变；对于添加轨道不平顺工况，迭代4次后，误差对数值由-1.83下降到-2.98并基本保持不变，2种工况误差结果满足误差小于阈值，可收敛至标准解的要求.

4 结论

1) 基于不动点迭代算法的离线迭代混合试验方法可以用于桥上行车的混合试验研究.

2) 研究结果均基于振动台能够稳定复现的前提，振动台复现精度的降低会对最终收敛结果造成一定的误差.

3) 不动点迭代算法可实现信号快速收敛，对于代表实际干扰的白噪声输入和轨道不平顺输入，分别经过6次和4次迭代，可以稳定收敛.