基于多项式混沌的激光大气传输湍流效应不确定度量化
杜配冰,刘 钰,陈志华,关 奇,夏洪富,蔡利兵
(西北核技术研究所,西安710024)
激光在大气中传输时会出现光束扩展及功率密度下降等一系列湍流效应,使激光系统的使用效果发生变化[1-2]。数值模拟是研究激光大气传输湍流效应的重要手段之一,数值模拟中常用的方法是采用多层相位屏模拟大气湍流特性,再通过傅里叶变换求解激光的传输过程[3-4],一般只针对确定的输入参数进行计算。由于现实条件下激光器与大气环境均非绝对稳定,激光器及大气参数均存在着较大的随机不确定性,这严重影响了数值模拟结果的可信度。近年来,张建柱等分析了大气参数的测量不确定度对激光大气传输到靶平均功率密度的影响,结果表明,当湍流越强且热晕越弱时,大气相干长度的测量不确定度对计算结果的影响越大[5]。陈志华等研究了激光大气传输到靶平均功率密度的外推计算方法,并分析了近场激光功率密度和大气传输修正系数的不确定度,结果表明,当测量路径上的大气相干长度大于8 cm且外推路径上的发射仰角大于35°时,可以采用几何外推方法计算到靶平均功率密度[6]。
对激光大气传输湍流效应的数值模拟结果进行不确定度量化,可减少不确定性带来的风险,并有效提高数值模拟的预测能力[7-8]。蒙特卡罗(MC)方法是不确定度量化中最常用的方法,具有操作简单和适用性强等特点[9]。但MC方法的均值收敛率过慢,需要使用大量样本进行数值模拟才能得到较精确的结果,因此计算成本过高。近年来,多项式混沌方法在不确定度量化计算中的应用越来越广泛。例如,王瑞利等针对爆轰问题研究了JWL模型的多项式混沌不确定度量化方法[10];伍月千等基于多项式混沌方法研究了电磁波入射角对孔缝结构机箱中心点电场强度幅值的影响[11];万华平等研究了针对结构动力特性的多项式混沌不确定度量化方法[12]。多项式混沌方法的核心思想是将随机解表示为随机输入参数的正交多项式展开形式,从而构建与数值模拟对应的多项式混沌代理模型。由于正交多项式序列存在高精度快速计算方法[13],所以,用代理模型取代数值模拟可有效降低数值模拟生成样本的计算开销。目前,国内外在激光大气传输的不确定度量化方面,尚缺乏多项式混沌方法的研究报道。
本文将多项式混沌方法与拉丁超立方抽样方法[14]相结合,建立了激光大气传输湍流效应数值模拟的不确定度量化方法;以地空垂直上行激光传输为例,考虑了激光器出口光束质量和大气相干长度的不确定性,计算了远场功率密度的不确定度,并与MC方法的计算结果进行了对比,验证了本文不确定度量化方法的精确性与有效性。
1激光大气传输湍流效应的数值模拟策略
激光大气传输的数值模拟通常包含真空传输和相位屏构造2个部分。激光在大气中的传输可用抛物型方程描述为
(1)
其中,k=2π/λ,λ为激光波长;u为入射光波在自由空间传输至(x,y,z)处光波电场的复振幅;n′为湍流引起折射率的起伏值。求解式(1)时,通常将大气传输路径分成若干段,每一段均设置薄相位屏以体现湍流的影响,其余部分设置为真空,结合傅里叶变换分段循环求解。
傅里叶变换谱反演法是构造相位屏的常用方法,主要是通过湍流的功率谱对随机矩阵进行滤波,再通过傅里叶逆变换得到大气扰动的相位[15]。
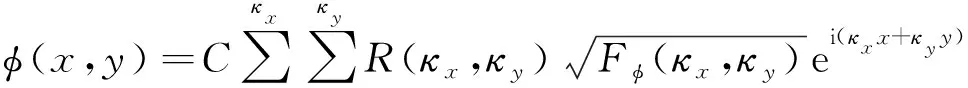
(2)
其中,κx,κy分别为x,y方向的相空间的波数;C为常数;R(κx,κy)为服从N(0,1)的高斯随机数;Fφ(κx,κy)为相位畸变的功率谱密度。
假设相邻的相位屏相距Δz,则第i个相位屏处光波电场的复振幅为
(3)
其中,f表示傅里叶变换;f-1表示傅里叶逆变换;τ(r)为相邻的相位屏之间由湍流引起的相位调制函数。
2多项式混沌方法
多项式混沌方法最早于1938年由Wiener提出[16]。该方法使用Hermite多项式基函数逼近带有Gauss型随机参数问题的随机解。随后,Xiu等通过Askey法则将多项式混沌方法推广到带有非Gauss型随机参数的问题,可根据随机参数的不同分布类型找到对应l2范数最优逼近的正交多项式基函数[17]。表1给出了常见概率分布函数对应的正交多项式基函数及其分布区间。

表1常见概率分布函数对应的正交多项式基函数及其定义域Tab.1Corresponding polynomial chaos basis of generalcontinuous probability distributions and their domain
对于带有n个独立随机参数X的不确定性系统Y(X),若X=(X1,X2,…,Xn) ,随机参数的联合概率分布函数FX(x)=P(X1≤x1,X2≤x2,…,Xn≤xn),随机参数Xi的边缘概率分布函数FXi(xi)=P(Xi≤xi),则
(4)
(5)
其中,i=(i1,i2,…,in),|i|=i1+i2+…+in,且0≤|i|,i1,i2,…,in≤N。构建一个关于目标函数y(X)的l2范数,逼近N阶正交多项式展开式,即
(6)
一元正交多项式基函数的正交性可表示为
E[bi(Xk)bj(Xk)]=
(7)
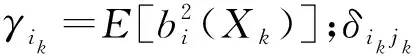
E[Bi(X)Bj(X)]=
(8)
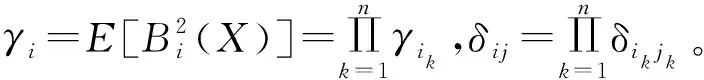
E[y(X)]≈E[yN(X)]=
(9)
目标函数的方差为
(10)
其中,ci可根据基函数的正交性由式(7)得到,即
(11)
采用多项式混沌方法逼近光滑函数的收敛速度随N呈指数增长,构建代理模型的计算开销主要用于求解多项式展开系数[18]。由于MC方法的收敛速度低于线性收敛速度,所以采用式(11)求解系数所需的样本量过高,严重降低了计算效率。因此,可随机抽取少量样本,采用最小二乘回归方法求解系数,即
(12)
3算例
本文对激光大气传输湍流效应数值模拟进行不确定度量化时,根据文献[5],主要考虑输入参数带来的不确定性,以激光器出口光束质量β0和大气相干长度r0为不确定性来源。
选取激光为准直Gauss光束,大气能见度和传输距离均为10 km,接收面为5 000 mm×5 000 mm的正方形,传输路径为垂直上行传输,大气折射率结构常数选用Hufnagel-Valley5/7参数模型,折射率起伏谱选用Kolmogorov模型。结合不确定性参数的统计分布随机特性[20],选β0为3倍衍射极限,r0为6.75 cm。根据文献[6],实验测量大气相干长度的不确定度应不大于7%,所以,本文假设在高斯分布场合下β0和r0的不确定度均为5%,即β0和r0均以99.73%的概率分别分布于3(1±5%)与6.75(1±5%)的参数空间中。
用MC方法进行激光大气传输数值模拟不确定度量化时,对β0和r0随机抽取10 000组样本,通过数值模拟可以得到10 000组远场光强分布的样本,归一化后得到的远场相对光强分布,如图1所示。
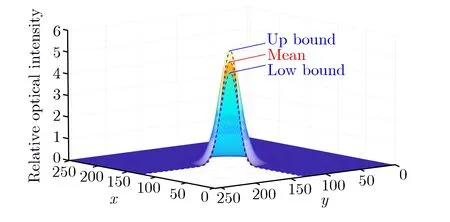
图1用MC方法得到的10 000组样本的远场相对光强分布Fig.110 000 samples of far-field relative optical intensity distribution calculated by MC method
采用随机抽样方法和拉丁超立方抽样(LHS)方法对β0和r0随机抽取20组样本,抽样结果的对比如图2所示。其中,图2(a)为随机抽样方法抽取的20组样本,图2(b)为LHS方法抽取的20组样本,图2(c)和图2(d)为随机抽样方法和LHS方法抽取样本对应的累积分布函数(CDF),由于LHS方法将CDF等分成若干区域后再分别进行随机抽样,所以抽取的样本更均匀。
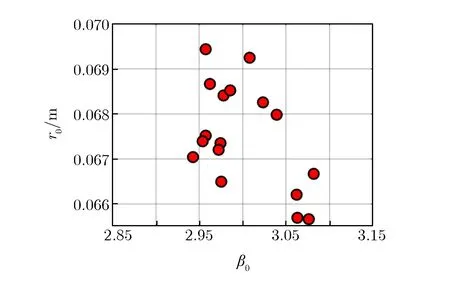
(a)20 samples by random sampling
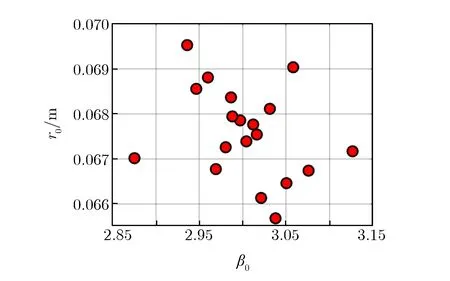
(b)20 samples by LHS
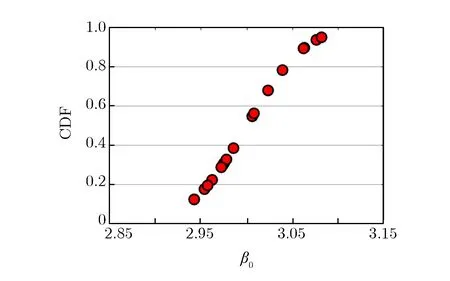
(c)CDFs of 20 samples by random sampling
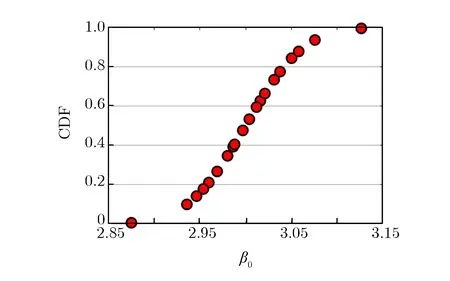
(d)CDFs of 20 samples by LHS
抽取样本后进行数值模拟,根据多项式混沌(PC)方法和表1,选取Hermite多项式构建远场功率密度的代理模型,用代理模型代替数值模拟,将随机抽取的β0和r0样本代入代理模型,最终得到归一化后远场相对功率密度均值,如表2所列。远场相对功率密度的不确定度及其与MC方法的相对偏差,如表3所列。由表2可见,PC方法与MC方法得到的远场相对功率密度均值比较接近。由表3可见,PC方法与MC方法的相对偏差基本上随着PC展开阶数与样本数量的增加而减小,当阶数为3且样本量为50组、阶数为4且样本量不小于30组及阶数为5时,相对偏差均小于5%,说明此时建立的代理模型具有足够高的计算精度。
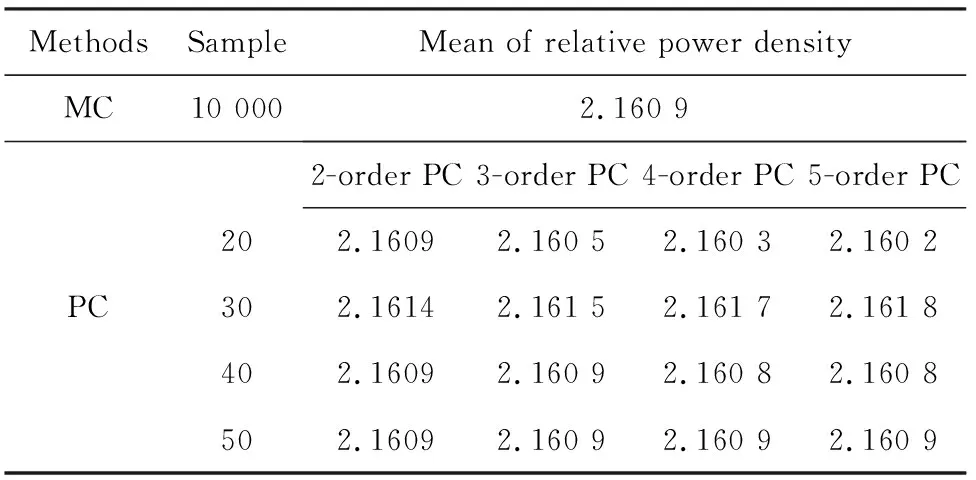
表2远场相对功率密度均值Tab.2Far-field means of relative powerdensity by MC and PC methods
由于所需生成的样本量越少,数值模拟的计算开销越小,所以采用20组样本和5阶PC方法构建的代理模型,将10 000组样本代入代理模型,计算得到样本数与相对功率密度之间的柱状图,如图3所示。其中,图3(a)为MC方法的结果,图3(b)为PC方法的结果。根据图3分布,估计得到远场相对功率密度的概率密度函数(PDF),如图4所示。由图4可得到MC方法与PC方法计算的远场相对功率密度的不确定度分别为18.7%与18.6%,二者依然吻合较好。
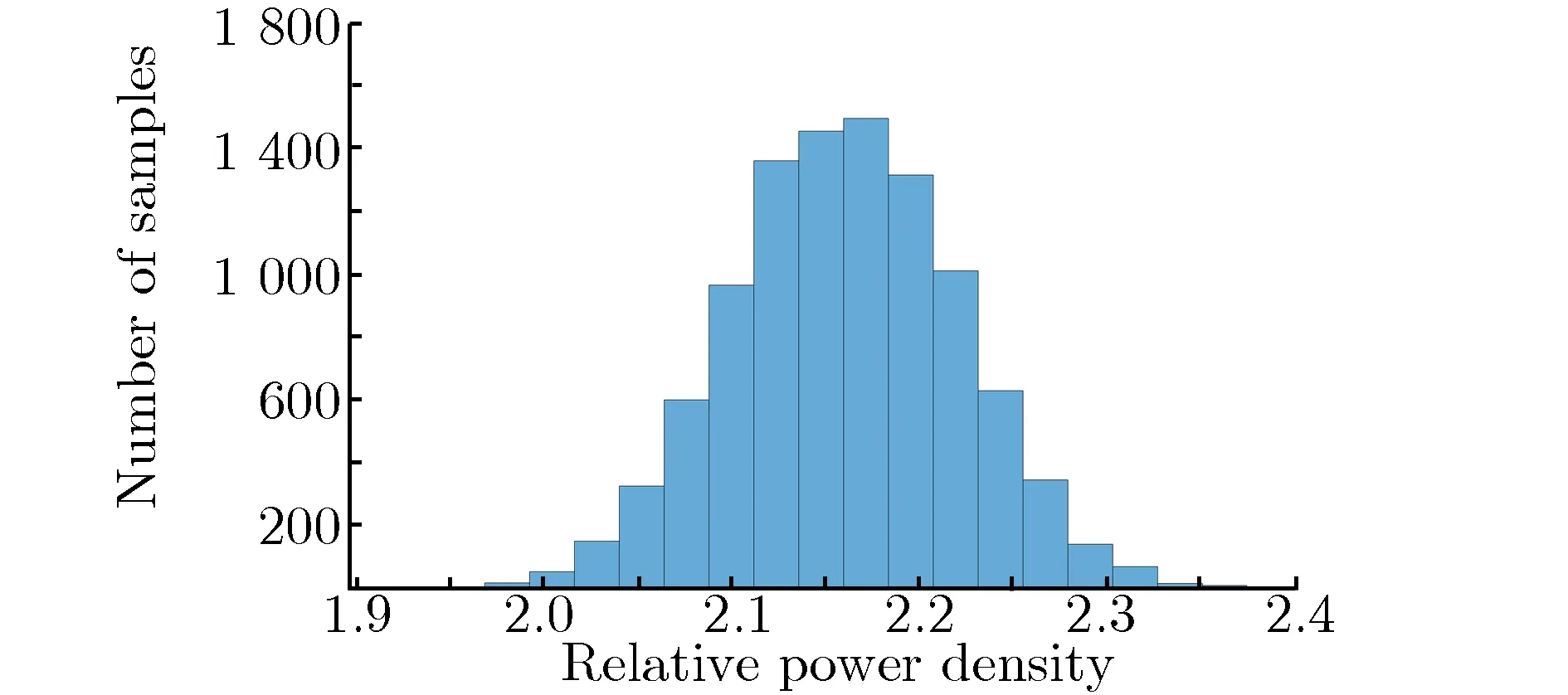
(a)Relative power density by MC method
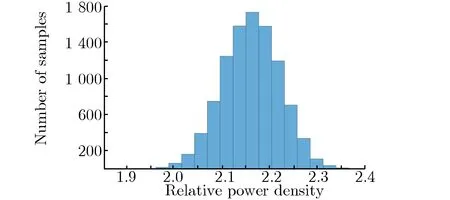
(b)Relative power density by 5-order PC method
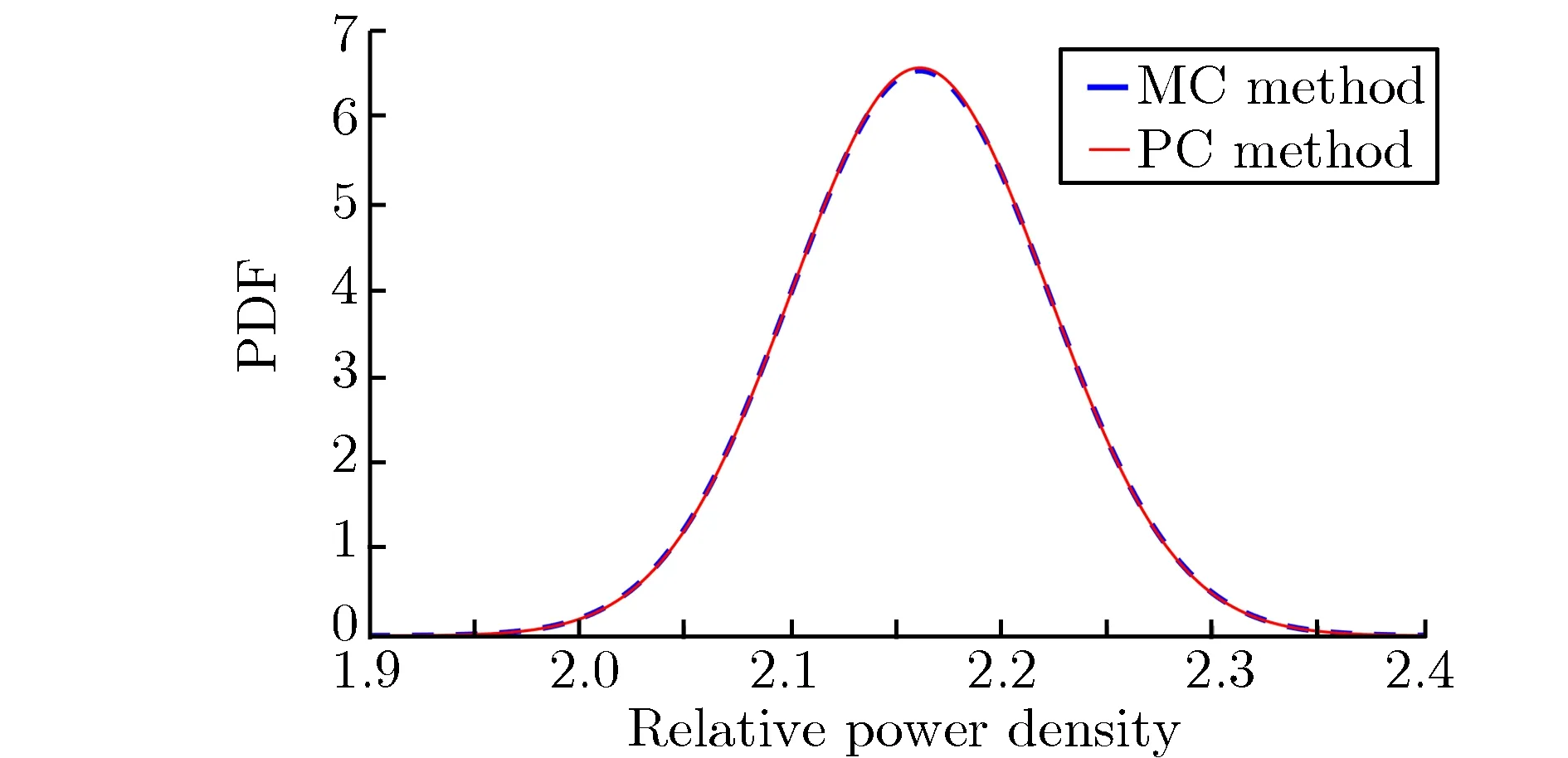
图4远场相对功率密度的概率密度函数Fig.4Probability density function of far-field relative power density
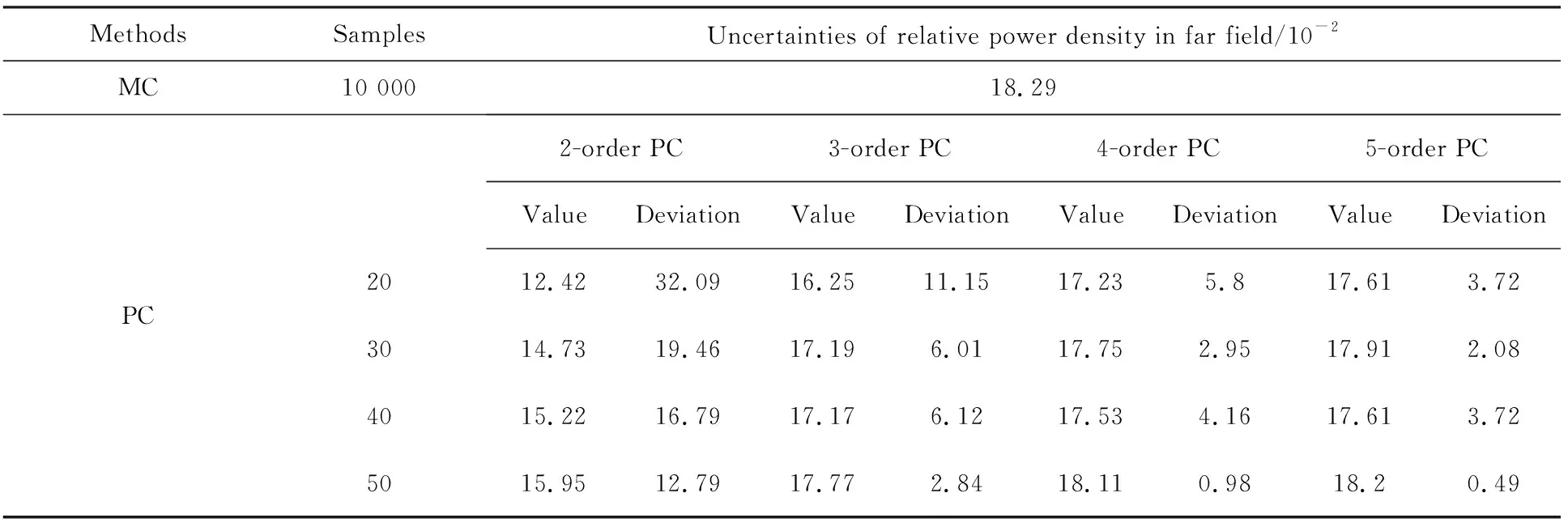
表3远场相对功率密度的不确定度及其与MC方法的相对偏差Tab.3Uncertainties of far-field relative power density and their relative deviations with MC method
4结论
本文针对现实条件下激光器与大气环境非绝对稳定的问题,建立了一种激光大气传输湍流效应数值模拟的不确定度量化方法。以出口光束质量与大气相干长度为不确定性来源,利用少量样本构建了多项式混沌代理模型,实现了远场相对功率密度的不确定度量化,在不损失精度的前提下大大提升了计算效率。

