天地一体化网络基于拥塞状态的路径选择算法

鄢砚军，徐慧慧，叶 升

(1.中国人民解放军91892部队， 海南 三亚 572099； 2.武汉大学 电子信息学院， 武汉 430072)

当前，地面第五代移动通信系统(5G)因高数据速率、低延迟和大规模连接特征成为通信业和学术界探讨的热点。然而，覆盖面积小和小型蜂窝小区有限的回程容量仍未解决，难以单独依靠地面网络实现中国领土、领海内信息网络全覆盖。随着低轨道(low earth orbit，LEO)卫星的快速发展，LEO卫星网络已显示出巨大潜力，可以与地面网络融合来解决上述问题。2018年，一些国家和组织宣布发射低地球轨道(LEO)通信卫星用于构建MSN为全球用户提供宽带互联网连接服务。同样，Oneweb计划发射648颗低轨卫星组成卫星通信网络用于全球卫星互联网宽带服务[1]。得益于高海拔、宽广的工作频谱和超密集拓扑结构，LEO卫星网络可以通过大容量回程、广阔的覆盖范围和灵活的接入技术支持大量用户通信[2]，通过地面段接入移动卫星通信网络终端[3]进行通信。

在天地一体化网络中，信息数据传输需要高带宽，但是终端业务存在不均衡的流量分布，难以保证最佳的端到端吞吐量，天地一体化路由算法在建立源终端与目标终端之间的最佳路径至关重要。研究人员对天地一体化路由方法[4-5]的研究主要方向是将地面路由协议扩展到卫星网络中，使用预先计算的网络拓扑来限制泛洪路由消息的数量。这些研究大多数适用于预先计算的拓扑，难以反映卫星网络的动态链路状态，对于卫星网络的高动态拓扑，应解决卫星动态路由问题。文献[6]提出基于虚拟拓扑的路由算法，该算法利用卫星轨道的周期特性和星座结构的可预测特性，在卫星运转的周期T内，将时间T离散化为n个时间片段。在某个时间片内，卫星的拓扑结构可虚拟为静态的拓扑图，用最短路径算法(dijkstra shortest-path，DSP)计算路由。文献[7]采用周期离散化的思想，提出有限状态的概念，将卫星系统的一个周期分为多个状态，将每个状态下的卫星拓扑连接视为静止，DSP算法能计算出每个状态内的全局最优路径，但该算法所有时间片内路由表的计算操作都是预先完成的，无法应对动态变化的网络结构。

国家安全和军事领域日益增长的移动数据流量需求使卫星网络得到了学术界和工业界的广泛关注，由卫星网络与地面网络互联互通的天地一体化信息网络被列入我国“十三五”规划纲要。同时当今世界正处于信息化战争时代，信息化战争是高度依赖信息保障的立体战争形态，天地一体化网络不受区域、地形影响，能够快速建立无线网络，为联合作战提供通信支持。

随着卫星网络用户的快速增长，卫星通信网络拥塞情况已不可避免。为提高数据传输效率，文献[8]采用了预测排队时延的方法避免拥塞。文献[9]提出基于“轨道代理”的方法，该算法收集每个相邻链路的排队时延，将时延信息转发给轨道上的所有卫星。在高流量负载下，由于报文传输时延大，收集的排队时延可能已过时。为避免拥塞，文献[10]提出了一种负载均衡(ELB)方案，在ELB中，当卫星链路变得拥塞时，它向邻居卫星发送拥塞通知，并要求邻居卫星降低发送速率。由于ELB没有考虑下一跳链路的时延，仍然无法有效防止部分链路拥塞。为解决这个问题，文献[11]提出了一种基于交通灯的智能路由策略，该策略根据当前ISL的队列时延来决定下一跳转发节点。该方法降低了报文丢失率，但算法的传输时延是固定值，下一跳的选择不是最佳解决方案，可能选择更长的路径传输数据，导致端到端时延变得不稳定，有时会异常高。

为解决天地一体化路由中拥塞问题，本文提出了一种基于拥塞状态的路径选择算法(routing selection algorithm based on congestion in ITSNs，RACA)。该算法根据极轨道星座和切斜轨道星座特点提出一种新的网络拓扑模型，相应给出了基于该模型的路由优化算法。该路由算法的路由选择以源地址和目的地址之间路径的最小传播时延和队列时延为准则，该算法是分布式的结构，即下一跳路由的选择基于当前时刻LEO卫星中的分组来决定，与其他LEO卫星和分组无关。然后通过模拟退火算法计算最优的天地一体化路由集合，在端到端时延的约束条件下，最大化端到端的可用带宽。

1 天地一体化网络路由和拓扑分析

1.1 天地一体化网络路由策略

由LEO卫星通信网络和地面网络组成的天地一体化网络联合作战架构如图1所示。卫星网络由N个极轨道和M颗卫星组成，每个地面终端到卫星终端同时连接卫星节点和地面节点。用户终端可以通过地面节点或卫星节点接入网络。每个卫星有5个端口，其中4个端口连接到4个相邻卫星，另一个端口连接到地面节点的端口。每个端口都可以配置一个性能计数器，该计数器用于计算报文的到达率和发送率，从而获得每个链路的排队时延。链路包含以下3种。

1) 轨内星间链路，它是同一轨道平面内相邻2个卫星节点之间的链路，记为Intra-ISL。

2) 轨间星间链路，它是相邻轨道上相邻卫星之问的链路，记为Inter-ISL。

3) 星地链路，它是地面终端与卫星之间的通信链路，记为GSL。

为了最大化源到目的终端之间的可用带宽，本文根据地面链路、星地链路和ISL中的可用带宽找到最佳路径。由于卫星的高移动性会导致ISL和星地链路的频繁变化，卫星路由算法直接影响天地一体化路由算法的性能。为此，本文首先基于每个ISL的通信时延，设计卫星路由算法，得出源到目的卫星之间的最小时延。然后，通过模拟退火算法选择一种最佳组合，在端到端时延的约束条件下，最大化端到端可用带宽。

1.2 拓扑分析

文献[12]使用了不同网络拓扑结构寻找极轨道星座的最短路由，但不能用于倾斜轨道星座。本文提出了一种新型的网络拓扑结构，可以适用于极轨道星座和倾斜轨道星座。极轨道卫星网络和倾斜轨道卫星网络的拓扑如图2、图3所示，本文将极轨道卫星网络和倾斜轨道卫星网络的立体星座分别从N极和S极的角度形成平面的拓扑结构。此时的平面网是由2张普通的网背靠背的叠加而成，这样源卫星在立体球面网络上传输数据给目的卫星的路由问题，变成了卫星在平面网络上寻找最短路由的问题。

图2 极轨道星座网络拓扑示意图

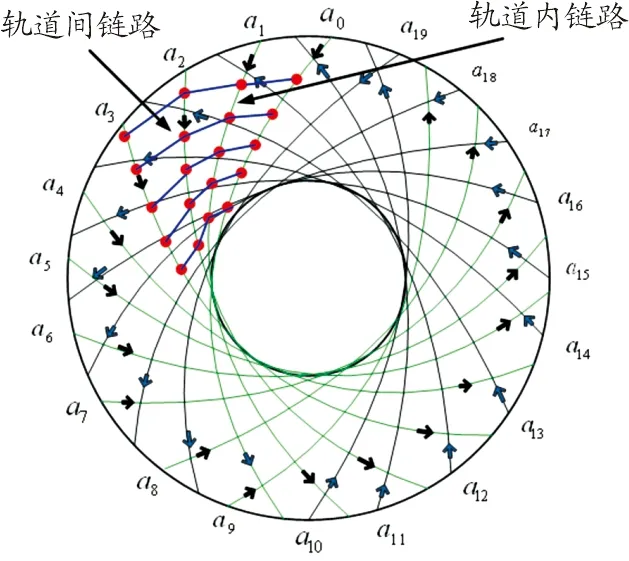
图3 倾斜轨道星座网络拓扑示意图

从图2中可以看出，所有轨道面内链路的长度是固定的，其计算公式为:

(1)

式(1)中：r表示轨道半径；M为单个轨道面上的卫星颗数；L表示轨道面内链路的长度。

2个相邻轨道面上的卫星之间链路长度为：

(2)

式(2)中：F代表轨道间的相位参数；N表示每个轨道的卫星个数；θ表示当前卫星节点的纬度。

2 路由算法

2.1 队列时延

链路的距离决定数据包通过链路的传播时延，网络的拥塞程度决定数据包通过的队列时延，本文定义链路的拥塞率为ci=λi/μi，i=1，2，3，4，λi是收到的相邻4个卫星的报文率，μi是给相邻4个卫星的发送率，λg是GSL报文到达率，μg是GSL报文发送率。si-sj之间的第n条链路的队列时延表达式为：

(3)

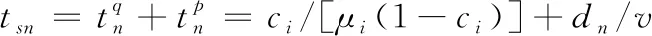
(4)

定义dsg为星地链路的距离，则GSL的通信时延表达式为：

tsg=cg/μg(1-cg)+dsg/v

(5)

2.2 卫星路由算法

本文提出的RACA路由算法中的各个网络节点只需要收集本节点和邻居节点的网络信息，对转发的数据报文计算下一跳节点，不需要收集全网的时延信息，路由信息交互较少。卫星节点地址以赤道为中心将地球分为南北2个极面，用0表示北极面，1表示南极面。我们定义源卫星和目的卫星的地址分别为(poles，rs，θs，ids)和(poled，rd，θd，idd)，其中pole表示极面，r表示卫星与极心的距离，θ表示极轨道星座卫星轨道与中心线的夹角，id表示卫星所处的轨道。

由于每个卫星节点有4个方向的端口，当节点收到需要转发的数据时，首先确定可以转发数据的端口。在当前节点(poles，rs，θs，ids)收到发往目的节点(poled，rd，θd，idd)的数据时，首先记录数据的入口方向，该方向在任何情况下都不会成为数据的下一跳方向；然后计算目的节点所在的方向，以保证数据包能以最少时延到达目的节点。当前节点选择下一跳的方法的相对地址表示如下:

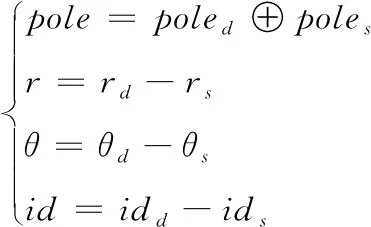
(6)

式(6)中：pole的取值为0或1，0表示源节点和目的节点在相同极面，1表示在不同极面；r表示卫星与极心的距离，当r>0时，表示目的地址在源地址的外环上，当r<0时，表示目的地址在源地址的内环上；θ为正数时，表示目的节点在源节点的逆时针方向，θ为负数时，表示目的节点在源节点的顺时针方向；id=0表示目的地址和源地址在相同的轨道上，id≠0表示目的地址和源地址在不同的轨道上。

2.2.1相同极面时的情况

1)id=0，进一步对比r，r>0时，内环方向的节点不会成为数据的下一跳方向，记录数据的入口方向，该方向在任何情况下都不会成为数据的下一跳方向；当r<0时，外环方向的节点不会成为数据的下一跳方向；最后对比剩下候选方向的邻居节点的传输时延和队列时延，选择最短通信时延的候选邻居为转发的下一跳；当r=0时，表示当前卫星就是目的节点卫星。

2)id≠0，首先记录数据的入口方向，该方向在任何情况下都不会成为数据的下一跳方向；然后对比r和θ，当θ>0且r>0时，目的卫星在当前卫星的右上侧，确定候选节点为内环和右方向的节点；当θ<0且r>0时，目的卫星在当前卫星的左上侧，确定候选节点为内环和左方向的节点；当θ<0且r<0时，目的卫星在当前卫星的左下侧，确定候选节点为外环和左方向的节点；当θ>0且r<0时，目的卫星在当前卫星的右下侧，确定候选节点为外环和右方向的节点；最后对比剩下候选方向的邻居节点的传输时延及队列时延，选择有最短通信时延的候选邻居为转发的下一跳。

2.2.2不同极面的情况

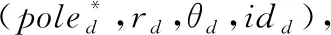
2.3 路径选择算法

基于提出的卫星路由算法，si-sj之间的通信时延tsisj为：

(7)

对于源终端到目的终端u0-ud之间的数据传输，其端到端的通信时延由tu0si和tsjud组成。tussi表示源终端us到卫星节点si的通信时延；tsjud表示卫星节点sj到目的终端ud的通信时延，其计算公式分别为：

tussi=tusgi+tgisi，gi∈W，si∈S

(8)

tsjud=tgjud+tgjsj，gj∈W，sj∈S

(9)

式(8)～(9)中：tusgi表示u0到地面-卫星终端gi的通信时延；tgjud表示gj到ud的通信时延；tgisi和tgjsj表示星地间的通信时延。

由于地面网络的拓扑结构是固定的，源终端使用bellmanford 路由算法计算出u0-ud之间的路由和该路由上的地面终端节点到卫星终端节点。并搜集u0-ud路径上所有链路的流量状态信息，然后通过路由更新周期内的历史链路流量来预测地面节点的每条链路流量，从而获得该链路的队列时延。由于u0-ud路径上所有链路的传播距离是固定的，传播时延可以通过传播距离计算，因此本文可以得到地面必经链路的通信时延，即tu0gi和tgjud。

用无向图G(V，E)表示天地一体化网络，其中V为网络节点集(包括地面和卫星节点)，E为节点之间的物理链路集，链路权重表示节点之间的通信时延。设定地面网络节点集Vc⊂V和地面终端到卫星终端数目k，由于数据传输需要高带宽，定义Cs、Cs分别为卫星链路和地面链路的带宽容量，Lsn、Lun分别为第n条卫星链路和地面链路传输的报文总长度，Tsn、Tun分别为数据流量在第n条卫星链路和地面链路传输所需时间，本文目的是找出连接卫星网络的地面终端到卫星终端的一个子集{g1，g2，…，gk}⊆W和卫星子集{Si，…，Sj}⊆S，最大化源终端到目的终端的可用带宽R，表达式为：

(10)

模拟退火算法的具体步骤为：

Input：G(V，E)，tmax

Output：Wopt，Rmax；

1： Initialize 初始温度β，终止温度βfinal，退火系数α；

2： 从Vc集合的n个节点中随机选择k个初始地面-卫星终端和为其服务的源-目的卫星节点对集合Wopt；

3： 计算时延(tsisj+tsjud+tu0si)；

4： if (tsisj+tsjud+tu0si)≤tmaxthen

5: whileβo>βfinaldo

6：Wnew=Wopt；

7： 生成新的集合Wnew；

8： 计算可用带宽Rmax；

9：Δ=Rnew-Rmax；

10: 生成一个(0，1)的随机数；

12：Wnew=Wopt；

13：tnew=tmax；

14： end if

15:β=β.α；

16： end while

17： returnWopt，Rmax。

我们设定源节点到目的节点的地面至卫星终端个数为k，其解空间集合的容量是k(k-1)/2，具有有限的数据量，考虑模拟退火算法过程简单，能快速求出从所有源终端到目的终端可用带宽的最大化最佳组合，我们采用模拟退火算法进行计算。

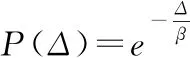
3 仿真

仿真场景中的卫星网络由156颗卫星组成，均匀分布在13个轨道上，高度为1 000 km，仿真参数见表1。仿真时在STK中创建星座模型，建立链路，在Qualnet中实现仿真模拟通信过程。在天地一体化路由算法中卫星路由算法决定天地一体化路径的选择，为了验证天地一体化路由方案，将RACA算法与ELB和DSP卫星路由算法进行对比。设置600条On-Off流，平均突发时间和平均空闲时间设置为200 ms，源终端和目的终端均匀分布，分为6个大陆区域，数据流分布见表2。源节点以0.8 Mbit/s至1.5 Mbit/s的恒定速率发送数据。

表1 仿真参数

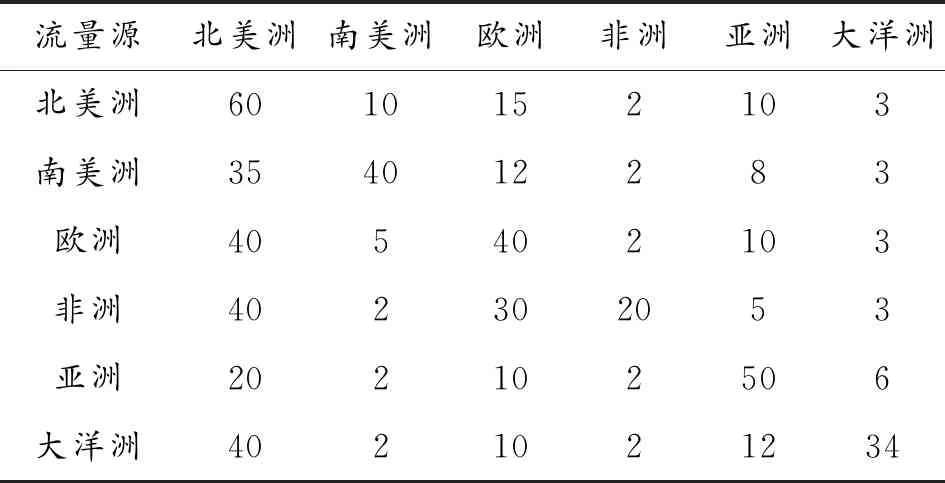
表2 数据流分布 %

3.1 端到端时延。

端到端时延是指源终端发送数据流量到目的终端需要的时间。从图4可以看出，DSP算法的平均端到端时延要比其他算法高，原因是DSP算法一直在最短路径上传输数据流量，随着数据流量的增加，链路开始拥塞，所选最短路径排队时延增加，导致平均端到端时延大幅增加。ELB算法响应拥塞动态地将流量绕道到备用路径，因此ELB算法端到端时延低于DSP算法。

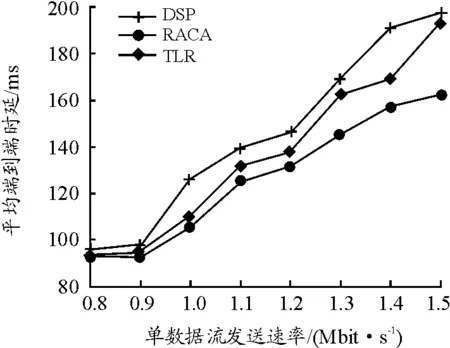
图4 不同速率下的端到端时延曲线

对比ELB算法和RACA算法发现ELB的传播延迟是恒定的，通过具有较高传播延迟的路由发送数据包，造成ELB算法端到端时延比RACA算法高。本文提出的RACA算法在3种方案中均实现了最低的平均端到端时延，这是因为所提出的路由算法的传输时延是时变的。该算法选择传播时延和排队时延中最小的路径，一定程度缓解了拥塞。

图5显示了3种算法数据丢包率的变化趋势，每条流的数据发送速率在0.8～1.5 Mbit/s的范围内变化，

图5 不同速率下的丢包率曲线

从图5可以看出，RACA算法的丢包率最低。这是因为在所有速率中，DSP算法始终选择最短路径传输数据，发送速率增大时，链路会出现拥塞，造成所选路径报文溢出，丢包率情况加大。ELB算法考虑了下一跳的拥塞，避免了队列的溢出，但ELB算法传输时延是固定值，ELB算法绕行的路径可能包括拥堵区域，造成丢包率增加。

3.2 地面传输和天地一体化传输性能对比

为了验证天地一体化路由的性能，图6表示地面路由和天地一体化路由的吞吐量。在没有拥塞的条件下，地面有足够的网络带宽满足用户流量的需求，使用地面路由的时延最短，此时，TSHR选择的路径与地面路由选择的最短路径相同，在地面链路没有拥塞时，地面网络和TSHR网络传输的吞吐量相同，在150 s时，由于流量需求的增加，节点开始拥塞。在地面路由算法中，一直选择最短路径会使数据流量集中该路径上，导致该路径节点负载过重。而在天地一体化路由算法中，卫星节点参与到数据包的转发工作，通过卫星网络更改路径避免选择地面拥塞的链路，提高数据传输的吞吐量。

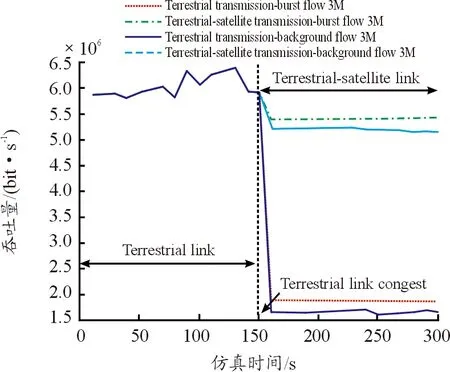
图6 地面传输和天地一体化传输的吞吐量曲线

4 结论

本文针对通信网络数据传输拥塞的问题，提出将卫星网络融合到地面网络中，并提出一种天地一体化网络传输路由算法RACA，根据地面段内以及地面和卫星段之间的流量需求调整路由。为了降低拥塞导致的队列时延，首先提出基于ISL通信时延的卫星路由算法，该算法通过计算每个方向上的ISL时延，找到最佳下一跳。然后以最大化路径的可用带宽为目标，通过模拟退火算法计算最优的天地一体化路由集合。在Qualnet中对RACA算法、ELB算法和DSP算法进行了仿真对比，结果表明，本文提出的RACA路由算法在端到端时延和丢包率方面均优于其他2种算法。同时对比了拥塞状态下天地一体化路由算法和地面路由算法，仿真结果表明天地一体化路由算法能为终端提供较好的吞吐量。