海沟模型及钢悬链线立管疲劳寿命预测研究*

娄 敏 庄肃然 时 晨

(中国石油大学(华东)石油工程学院)

0 引 言

海底地层中蕴含丰富的石油与天然气资源，各大石油公司都将石油资源开发的目标投向了深海。近几年，钢悬链线立管(Steel Catenary Risers, SCR)在深海油气输送领域中广泛使用。早在1994年，壳牌公司首次将SCR用于872 m水深的张力腿平台。经过了20余年的发展，SCR被成功应用于TLP(Tension Leg Platform)平台、SPAR平台、半潜式平台和FPSO(Floating Production Storage and Offloading)等多种平台，最大应用水深超过了3 000 m。另外，由于SCR具有经济性好、管径大、承压等级高、安装简单以及耐久性好等特点，被一致认为是技术可行、经济划算的深水油田立管解决方案。

海洋环境条件十分复杂，海洋结构物面临着波浪和海流等多种环境载荷以及内部载荷的共同作用问题[1-2]，可能会发生疲劳失效破坏，造成巨大的经济损失、严重的环境破坏，甚至人员伤亡，因此对它们的疲劳寿命评估至关重要。对于SCR来说，其在触地区域的疲劳表现一直是业内关注的问题，因为它会与海床土体相互作用形成一定深度的海沟，而海沟的存在会严重影响SCR的疲劳表现。白兴兰等[3]开发了一套小比尺钢悬链线立管整体分析试验装置，用来研究海床土体对立管触地区域动力响应的影响。在管土相互作用的模拟研究中，C.P.PESCE等[4]证明了线弹性海床模型可以较好地模拟出立管与海床的相互作用。杜金新[5]提出了一种简化的模型来表示立管与海床之间的相互作用。P.E.VOIE等[6]详细地计算了立管与海床土体之间的相互作用关系，并探究了立管响应对于哪种相互作用关系较为敏感。A.NAKHAEE等[7]开发了CABLE3D程序，用来准确地评估立管土体的相互作用。R.HEJAZI等[8]提出了一种等价线性刚度土体模型，用来评估立管与土体的相互作用。M.RANDOLPH等[9]提出了非线性滞后海床模型，该模型给出了土体吸力和土体刚度在SCR不同运动情况下的详细变化信息，目前该模型已被加入到商业软件Orcaflex中并被广泛应用于工程设计。

在工程实际中，海沟的存在对于SCR触地区域疲劳破坏的影响通常被忽略，这主要是因为通过有限元软件模拟海沟的形成需要花费大量的时间，所以在对SCR进行疲劳分析时常常采用平坦海床。为了解决这一问题，研究者们提出在对SCR进行动态分析前将海沟模型加入到有限元软件中，这样就会节省大量模拟时间。H.SHIRI[10]提出了两种海沟形状模型，分别是线性指数模型和二次指数方程模型，并且将这两种形状模型与ABAQUS软件中模拟出的海沟形状进行对比，发现当立管与土体相互作用循环次数超过1 000次时，二次指数海沟形状模型更贴近有限元软件模拟结果，然后将该模型加入到软件中分析其对立管疲劳寿命的影响。C.P.AUBENY等[11]提出了三次多项式海沟形状模型。以上提到的海沟形状模型是关于海沟对SCR触地区域疲劳破坏影响研究中应用最多的3种，若要建立完整的海沟模型，除了形状之外，还需要准确获得海沟的初始位置和长度。WANG K.P.等[12]提出了计算海沟长度与位置的方法以及参数方程，但在应用参数方程时发现存在一些错误，出现错误的原因在于他们对于合理海沟的定义不够准确，因此本文首先修正了合理海沟的定义并应用迭代法拟合出了更为合理的参数方程。

通过将3种海沟模型与Orcaflex动态模拟形成的海沟模型进行对比，发现三次多项式海沟模型不管是形状还是疲劳分析结果都与动态模型十分接近，因此在实际工程设计中，可以采用本文提出的新的参数方程结合三次多项式海沟形状模型来快速建立完整的海沟模型。最后应用该模型研究了海沟对SCR触地区域疲劳损伤的影响。

1 海沟模型

1.1 海沟形状模型

H.SHIRI[10]提出的线性指数模型为：

d(x)=-c1xe-c2x

(1)

其中：

(2)

(3)

二次指数模型为：

(4)

C.P.AUBENY等[11]提出的三次多项式模型为：

(5)

其中：

(6)

(7)

(8)

(9)

式中：d(x)表示在x处的海沟深度，m；x表示距离海沟起始点的距离，m；dmax表示海沟的最大深度，m；Lmax表示海沟起始点到海沟最大深度点的水平距离，m；LT表示海沟长度，m。

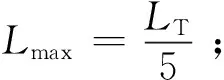
图1 海沟示意图

由图1可以看出，在海沟形成后触地点将朝向SCR的悬挂段移动。图1中TP代表海沟起始点和平坦海床时SCR的触地点之间的距离，且海沟起始点应位于平坦海床时SCR的触地点左侧，此时TP为负值。从以上3个海沟形状表达式来看，要想建立完整的海沟模型，还必须知道海沟的起始位置和长度。

1.2 WANG K.P.等[12]提出的参数方程

WANG K.P.等认为，当SCR的触地点位于海沟起始点和海沟最大深度点之间，并且SCR与海床自触地点到海沟终止点完全接触，此时的海沟为合理海沟。基于合理海沟的定义，他们应用迭代法来获得海沟长度LT和海沟起始点与平坦海床时SCR的触地点之间的距离TP，也就是海沟的起始位置。另外他们选择了三次多项式海沟形状模型来表示海沟形状。迭代法的简化流程如图2所示。

图2 迭代法的简化流程图

在他们的研究中，认为有3个关键参数会影响海沟长度LT和海沟位置TP，它们分别是海沟最大深度dmax、SCR单位长度质量M以及SCR的横纵跨度比H/V(从悬挂点到平坦海床触地点的水平距离与垂直距离的比)，将这3个参数以及LT和TP标准化为无量纲参数，即有：

(10)

(11)

(12)

(13)

(14)

式中：D为SCR的外径，m；ρ为海水密度，取值1 025 kg/m3。

研究中SCR的配置形式如图3所示。水深取1 000 m，立管总长度为1 610 m，立管内、外径分别为0.268和0.300 m，立管单位长度质量为175 kg，弹性模量为210 GPa，H初始值为361 m，拖曳力系数CD取0.7，附加质量系数CA取1.0。

图3 SCR的配置形式

从图3可以看出，V=995 m，H会随着悬挂角的改变而改变，RL和RTP均是Rd、Rm、RHV的函数。在他们的研究中，共选取了504组(Rd、Rm、RHV)，其中Rd取值1.5、2.0、2.5、3.0、3.5、4.0、4.5和5.0；Rm取值1.4、1.6、1.8、2.0、2.2、2.4、2.6、2.8和3.0；RHV取值0.361、0.456、0.560、0.675、0.803、0.954和1.129。

通过图2的迭代过程得出504组结果并拟合出了RL和RTP的表达式：

RL=72.5+30.9Rd+106.1RHV-

(15)

RTP=-99.2-12.7Rd+48.8Rm-30RHV+

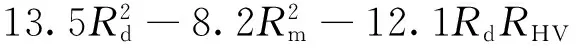
(16)

但是在应用过程中发现，通过上述方程计算的海沟长度和起始位置存在错误，导致建立的海沟模型并不符合他们研究中的合理海沟定义，下面选取一个算例来简单说明。

图4为Rd=4、Rm=1.6、RHV=0.803时SCR在海沟中的静态位置。图4中横轴代表海床上的水平坐标，纵轴代表垂直于海床向上的坐标，其值为负表示位于海床下面。黑色实线为SCR轮廓，红色点线为通过上述参数方程建立的海沟轮廓。从图4可以看出，此时触地点位于海沟最大深度点和海沟终止点之间，说明海沟的位置偏离SCR锚固点过远，并且SCR与海床自终止点到锚固点间存在间隙，即图中间隙区，这说明海沟的长度偏短。这个算例证明他们提出的参数方程不准确，这将会导致预测SCR在触地区域的疲劳表现时出现错误。

图4 SCR在海沟中的静态位置

1.3 改进后的参数方程

SCR静态轮廓与海沟轮廓不匹配是由于对合理海沟的定义不够准确，导致迭代循环跳出过早。为了获得能够准确计算海沟起始位置和长度的参数方程，本文将WANG K.P.等[12]在迭代法中关于合理海沟的定义修改为：当SCR的触地点位于海沟起始点和海沟最大深度点之间，并且SCR与海床自触地点到锚固点完全接触，而不仅仅是到海沟终止点，此时的海沟为合理海沟。

在重新定义合理海沟后，重复图2的迭代法。为了方便与WANG K.P.等[12]得到的参数方程进行对比，本文也采用相同的SCR配置形式和SCR参数配置，另外也选取了同样的504组(Rd、Rm、RHV)。相应地，生成了504组的RL和RTP。除此之外，还选择了相同的方程形式，即二阶多项式，经过敏感性分析去掉不重要的项之后，拟合的方程式如下。

RL=492.4+47.5Rd-222.2RHV-296.8Rm+

(17)

RTP=-128.6-13.8Rd+83.4Rm-

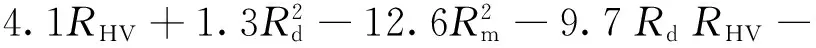
16.3RmRHV

(18)

接着应用改进后的参数方程计算了如图4所示算例的海沟长度和起始位置，结果如图5所示。图5中黑色实线代表SCR的静态位置，红色点线表示由改进的参数方程建立的海沟模型，蓝色虚线表示由原参数方程建立的海沟模型。由图5可以看出，SCR的静态位置与新的海沟轮廓十分匹配，说明用改进后的参数方程建立的海沟模型更为合理。

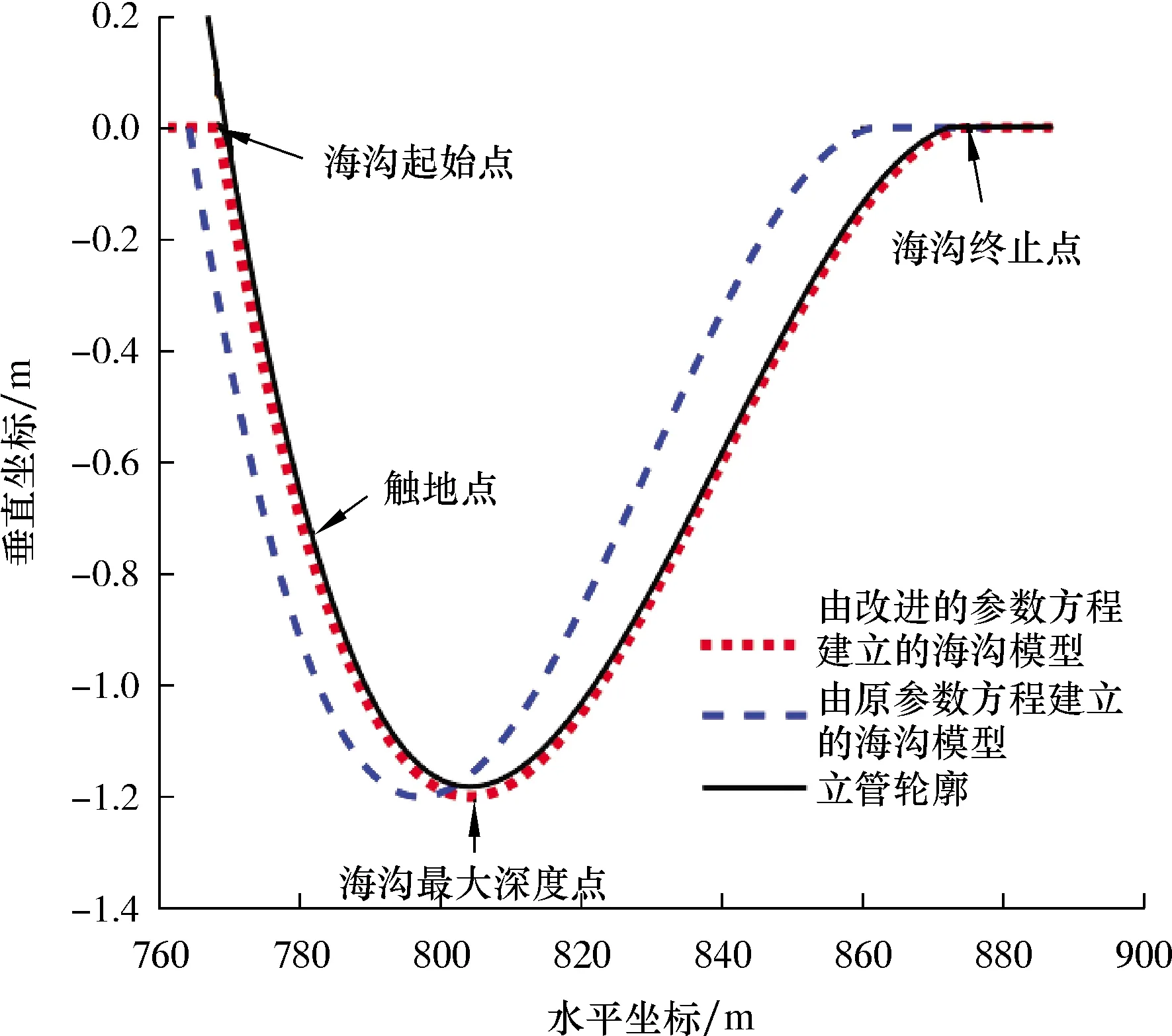
图5 SCR在改进的参数方程海沟中的静态位置并和原参数方程海沟位置对比

2 参数方程验证与海沟模型对比

接下来，本文将应用改进的参数方程来计算海沟的长度和起始位置，并通过与Orcaflex动态模拟生成的海沟模型进行对比来验证参数方程的准确性。另外，通过与动态模型的轮廓和疲劳分析结果进行对比，找出3种海沟模型中最准确的一个。

2.1 海床p-y模型

M.RANDOLPH等[9]提出了非线性滞后海床模型，也就是p-y模型，目前该模型已被加入到商业软件Orcaflex中并被业界广泛应用。图6为p-y模型中海床法向反力与立管贯入深度之间的关系曲线。该模型的主要特点为：随着SCR贯入深度的增加，海床法向反力逐渐增大直到达到某一确定深度(见过程①)；然后立管由于浮体的运动被举升起来(见过程②)，此时海床反力将表现为吸力，它将吸引立管向下；在过程③中吸力会增大而在过程④中将会减小。另外，过程⑤、⑥、⑦是SCR重新贯入土体的过程，循环上述过程将会逐渐形成某一深度的海沟。

图6 海床法向反力与立管贯入深度的关系曲线

本文所采用的非线性土体参数以及数值如下。泥线剪切强度Su0取1.5 kPa，剪切强度梯度S取2.5 kPa/m，幂次参数a和b分别取6.5和0.25，标准化最大刚度Kmax取200，吸力比fsuc取0.6，吸力衰变参数λsuc取0.5，重新贯入参数λrep取0.4，其中Kmax控制初始贯入曲线和举升曲线的土体最大刚度；fsuc控制吸力极限曲线；λsuc控制到达海沟最底部时吸力和最大反力释放速度；λrep控制重新贯入曲线以及举升曲线的相交位置。

2.2 验证参数方程

在Orcaflex中模拟海沟的形成需要花费大量的时间。H.SHIRI等[13]指出λrep可以控制海沟的发展速度，也就是说λrep越大，海沟的发展速度越快，所应用的时间也就越短，同时由于λrep的改变引起的其他效应可以忽略不记，所以应用Orcaflex进行动态模拟之前，将λrep设置为一个相对较大的值，经过30 min左右的模拟，海沟深度稳定在3D，通过这种方法得到的海沟模型在本研究中简称为“动态模型”。选取Rd=3、Rm=2.6、RHV=0.347，将动态模型的起始位置和长度与新的参数方程计算结果进行对比，其中动态模型的起始位置水平坐标为375.74 m，长度为57.25 m，参数方程的起始位置水平坐标为376.63 m，长度为55.66 m。由此可以看出，参数方程计算出的海沟起始位置和海沟长度与动态模型十分接近。

2.3 对比海沟轮廓以及疲劳分析结果

图7为Rd=3、Rm=2.6、RHV=0.347时，由新参数方程建立的三种海沟模型与动态模型轮廓对比。从图7可以看出，线性指数和二次指数海沟模型与动态模型相比有较大差距，三次多项式海沟模型与动态模型较为贴近。

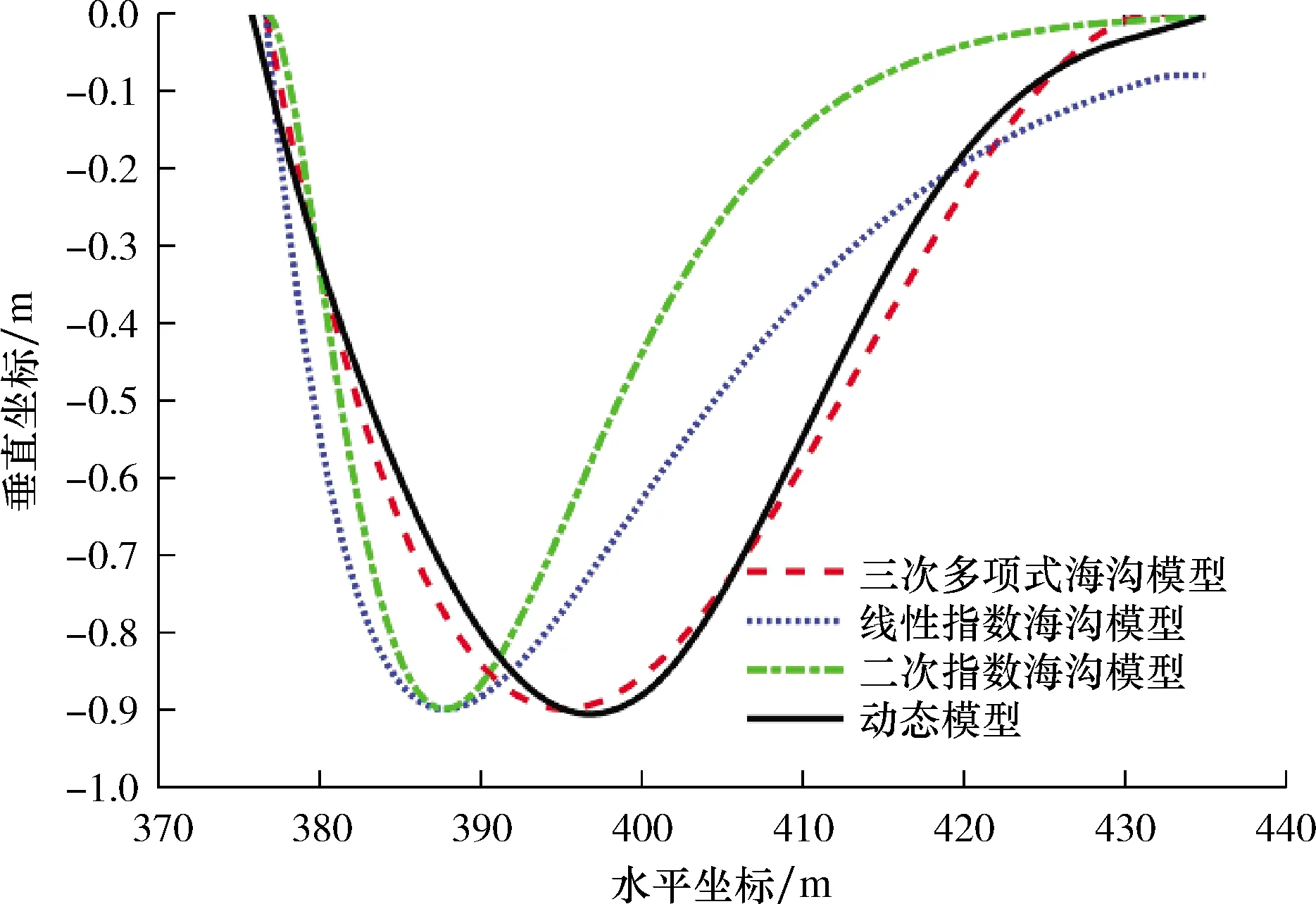
图7 海沟轮廓对比

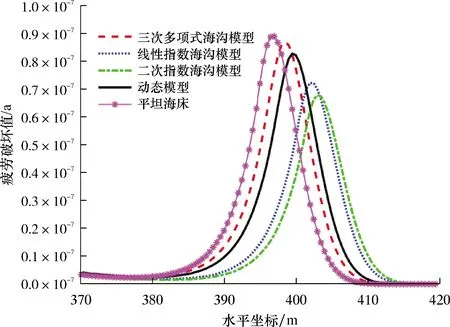
图8 SCR在触地区域的疲劳破坏值对比

综合图7和图8可以看出，在3种海沟形状模型中，三次多项式海沟模型与Orcaflex动态模型最为接近。

3 海沟对SCR触地区域疲劳表现的影响

为了探究海沟对SCR触地区域疲劳寿命的影响，下面对比了平坦海床和海沟存在时，SCR在触地区域的弯矩变化值，海沟模型使用的是三次多项式模型，海况参数同2.3节，结果如图9和表1所示。图9中黑色实线为应用Orcaflex动态模型的算例，红色虚线为应用三次多项式海沟模型时的算例，蓝色点线为应用线性指数海沟模型时的算例，绿色点画线为应用二次指数海沟模型时的算例，紫色星标线为平坦海床算例。表1中，平坦海床时，立管弯矩变化峰值为14 099.15 N·m，此时疲劳寿命为26 680 a；应用动态模型时，立管弯矩变化峰值为13 820.68 N·m，此时立管疲劳寿命为28 679 a；应用三次多项式模型时，立管弯矩变化峰值为14 018.09 N·m，此时立管疲劳寿命为27 781 a；应用二次指数模型时，立管弯矩变化峰值为13 091.28 N·m，此时立管疲劳寿命为34 980 a；应用线性指数模型时，立管弯矩变化峰值为13 317.80 N·m，此时立管疲劳寿命为32 855 a。

图9 弯矩变化值对比

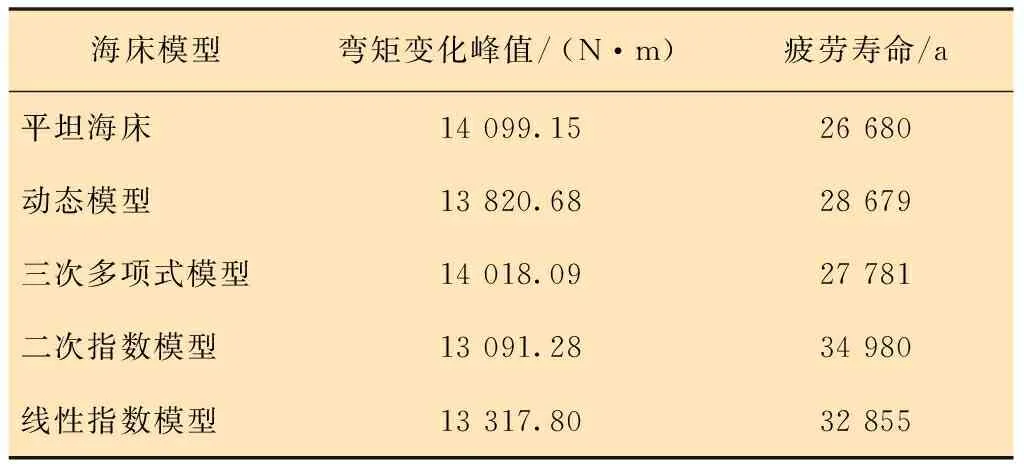
表1 弯矩变化峰值对比

由图9和表1可以看出，平坦海床时的弯矩变化值略高于海沟存在时，且平坦海床时立管的疲劳寿命最短，也就是说在该海况下，海沟的存在减小了SCR在触地区域的弯矩变化值，延长了SCR的疲劳寿命。

4 结 论

(1)之前关于海沟的研究中，有3种海沟形状模型应用较为广泛，分别是三次多项式模型、线性指数模型和二次指数模型。为了找出理想的海沟模型，重新定义了合理海沟，也就是当触地点位于海沟起始点和海沟最大深度点之间，并且SCR与海床自触地点到锚固点完全接触时，海沟是合理的。基于这个定义改进了文献提出的“静态迭代法”。

(2)采用了相同的变量和立管参数配置，然后根据改进的迭代法得到的数据，拟合出了新的参数方程用来计算海沟长度和起始位置，并结合海沟形状模型建立完整的海沟模型。

(3)通过与Orcaflex动态模型对比发现，改进的参数方程能够较为准确地计算海沟长度和起始位置，并且三次多项式海沟模型不管是轮廓还是疲劳分析结果都与动态模型十分接近，因此在工程设计中，应采用本研究提出的新参数方程结合三次多项式形状模型，以便快速建立完整合理的海沟模型。

(4)针对海沟对SCR触地区域疲劳表现的影响做了研究，通过与平坦海床对比发现，海沟的存在会减小SCR在触地区域的弯矩变化值，延长SCR的疲劳寿命。