燃料电池发动机空气系统改进内模解耦控制策略
孙田 陈光 景帅帅
(中国汽车技术研究中心有限公司)

由化石能源短缺和排放污染引发的能源危机已经成为当今社会发展的主要矛盾之一。燃料电池汽车与传统汽车相比,具有噪声低、效率高和零排放的优点。将燃料电池应用在重型卡车领域,可以有效避免体积限制,而且与纯电动重卡相比燃料电池重卡运行成本更加低廉。空气供应系统作为燃料电池发动机的一个子系统,会直接影响燃料电池的输出特性和动态响应,因此需要对其进行协调控制以满足系统的负载需求。近年来,国内外学者针对燃料电池发动机的空气供应系统开展了各类研究。文献[1-3]介绍了燃料电池发动机的建模方法。文献[4]在不考虑背压阀开度变化的基础上,采用自适应滑模控制方法对空压机供气量进行控制,实现了对过氧比的控制。文献[5]采用前馈模糊控制+反馈自适应PID的控制方案对空气流量进行控制避免氧饥饿现象。文献[6]针对大功率燃料电池发动机,根据负载大小对空压机进行分段控制以获取期望的流量。对于空气供应系统,空气进气流量和压强具有耦合关系,在实际应用中必须考虑协调控制以实现对空气流量和压强的独立控制。文献[7]基于线性二次调节器理论对空气流量和压强进行协调控制。文献[8-9]分别采用前馈补偿解耦和传统内模解耦对高压燃料电池的空气供应系统实现了解耦控制。在其他领域中,学者针对耦合系统的研究也提出了一些解决方案[10-13]。文章通过改进内模解耦控制算法,采用改进型Butterworth滤波器对内模解耦控制策略进行优化,实现对重卡用燃料电池发动机空气供应系统中空气流量和压强的解耦控制,提高了控制效果。
1 燃料电池发动机原理及建模
为保证燃料电池能够输出电能,需要向电堆入口持续供给充足的气体参加电化学反应。燃料电池的阴极需要供给氧气或空气,在电堆内部发生还原反应:

在燃料电池发动机中,空气供应会影响电堆输出和动态特性,供气供应系统组成如图1所示。大气中的空气经空气过滤器过滤掉固体杂质,进入空压机加压提升空气质量流量。离心式空压机具有结构紧凑、响应速度快、使用寿命长的特性,在车用燃料电池发动机系统中被广泛应用。空气经冷却、加湿以获取适宜的温度和湿度,进入燃料电池参加电化学反应。电子节气门连接在燃料电池阴极出气流道,其开度可以调整背压大小,对空气进气流量和压强进行调节。
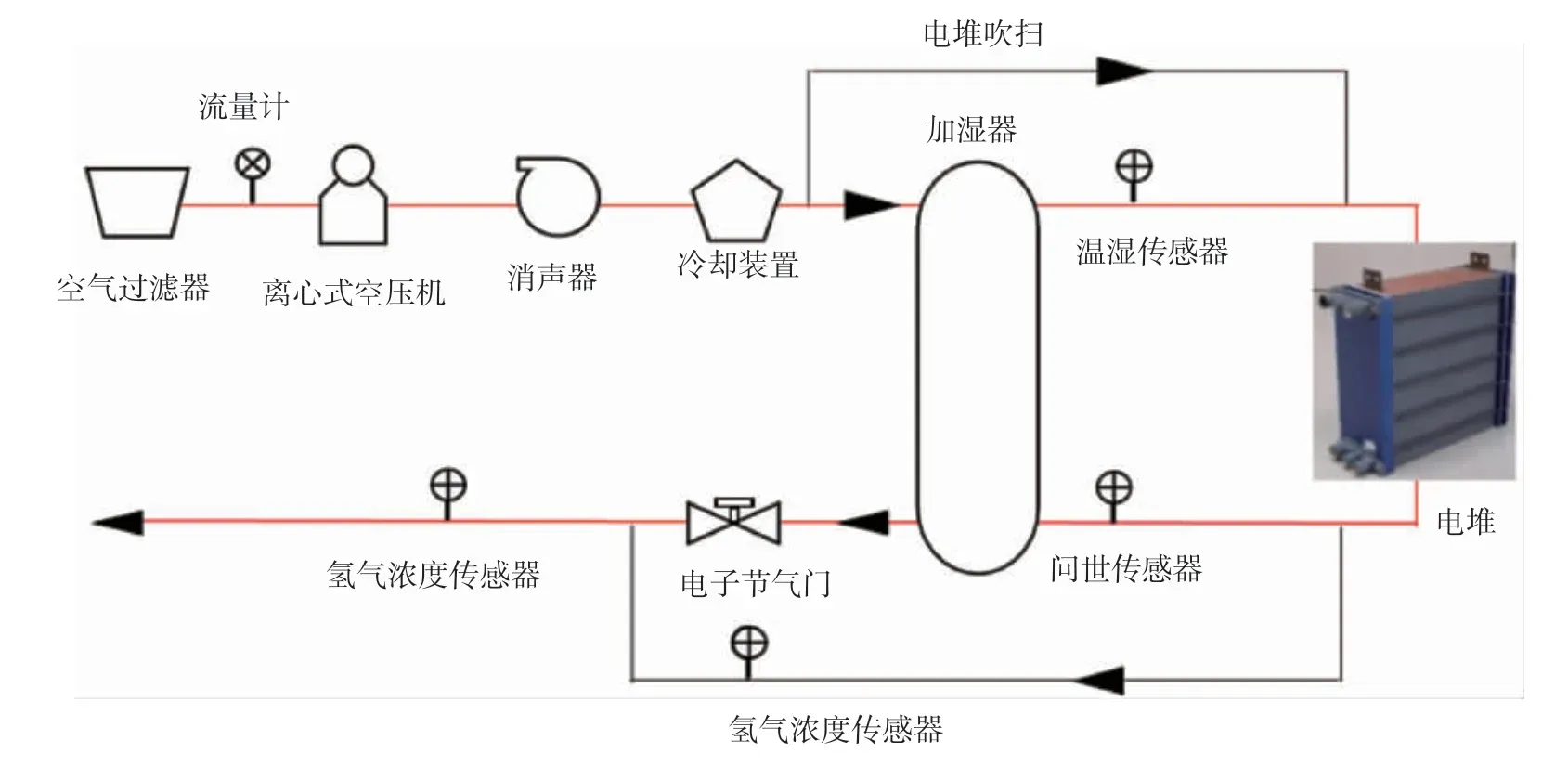
图1 燃料电池发动机空气供应系统组成
在不考虑温度和湿度的变化下,燃料电池阴极入口处的空气进气流量和压强是由离心式空压机和电子节气门的工作状态共同决定。空气进气流量和压强会影响燃料电池输出特性,压强如果过大会对质子交换膜产生损害影响燃料电池寿命,因此希望控制器能够对空气流量和压强进行独立控制。
基于搭建的燃料电池发动机台架,如图2所示,进行试验采集数据,建立以离心式空压机输入电压和电子节气门开度为输入,空气进气流量和压强为输出的两入—两出系统,对空气供应系统的动态试验数据进行辨识,系统传递函数矩阵为

图2 燃料电池发动机试验台架
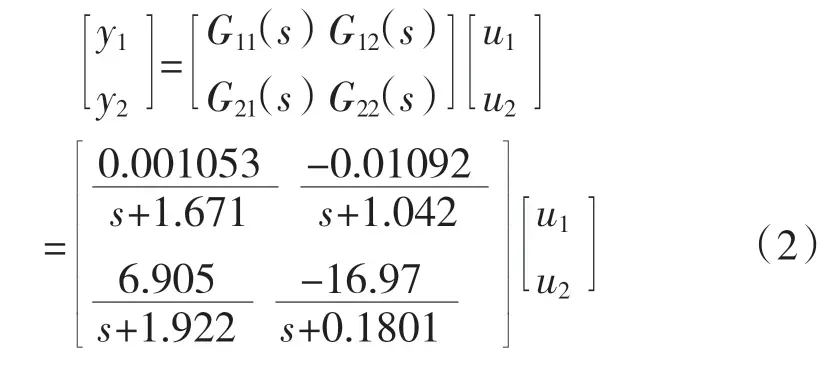
式中:y1、y2——系统输出:空气流量(g/s)和压强(kPa);
u1、u2——系统输入:空压机输入电压(V)和电子节气门开度;
s——拉普拉斯微元;
G(s)——各自通道的传递函数。
由传递函数矩阵可以看出该系统为耦合系统,为了达到良好控制效果对系统进行解耦控制。
2 燃料电池发动机空气系统改进内模解耦控制策略设计
燃料电池发动机空气系统中,空压机与电子节气门工作状态共同影响供给空气的流量和压强,因此采用解耦控制策略实现对空气进气流量和压强的独立控制,控制方案如图3所示。

图3 燃料电池发动机空气系统解耦控制方案
2.1 内模解耦控制原理
内模解耦控制策略将内模控制原理和解耦控制原理结合,属于鲁棒解耦控制策略的一种,具有参数少、鲁棒性强的优点,可以很好解决系统的耦合问题。
内模解耦控制系统的结构原理如图4所示。
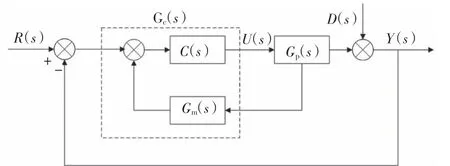
图4 内模解耦控制结构原理
其中GC(s)为反馈控制器传递函数,由结构图可推导出输入输出关系为
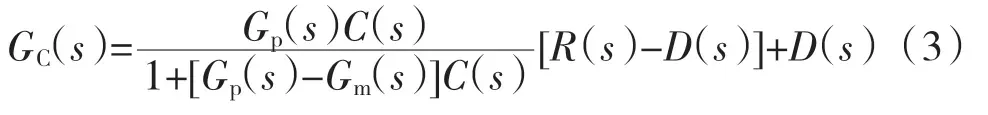
当系统为稳定系统不考虑干扰时且模型精准匹配时,此时该闭环系统的内模控制结构的传递函数为

可见当闭环传递函数矩阵Gm(s)C(s)为对角矩阵时,系统可以实现单输入对应单输出的解耦控制。C(s)作为内模解耦控制器传递函数,会直接影响控制精度、响应速度等控制质量,最为常用的内模控制器设计方法为零极点对消法,即:
其中,f为滤波器传递函数,Gm-(1s)为对G(ms)的求逆过程。
滤波器的参数会影响控制器的控制效果,因此调整滤波器参数可以对系统响应速度、鲁棒性进行调节。传统内模解耦控制原理中,滤波器通常采用一型低通滤波器,形式如下:

2.2 基于改进型Butterworth滤波器内模解耦控制策略设计
标准型Butterworth滤波器为全极点配置的一种低通滤波器,且响应幅度较为平坦,当零点在s=∞处时,标准Butterworth滤波器的传递函数为
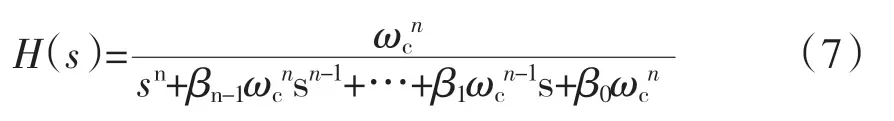
标准Butterworth滤波器的极点都均布在以截止频率为半径的左半圆上,由分布规律可知当离虚轴最近的一堆共轭极点与虚轴之间的夹角为

因此截止频率ωc不变的情况下,增加阶次n,会导致夹角θ减小,而系统的阻尼振荡频率为

随着夹角减小阻尼振荡频率增大,上升速度加快,阻尼比会减小,引发更强的振荡,加剧系统的不稳定性。
针对标准Butterworth滤波器随着阶数n增大系统更加不稳定的情况,提出改进型Butterworth滤波器,固定夹角θ不变,使其不随阶数变化而变化,其他极点均分布在单位圆上,改进型的Butterworth滤波器传递函数为:

对于n阶改进型Butterworth滤波器,其传递函数分为奇数和偶数2种情况。n为奇数时,传递函数形式为:

n为偶数时,传递函数形式为:

此时,基于改进型Butterworth滤波器的内模解耦控制器传递函数为:

其中,f1为改进型Butterworth滤波器的传递函数。
3 燃料电池发动机空气系统仿真结果分析
改进型Butterworth滤波器中影响控制效果的参数主要是阶次n和截止频率ωc,为探究各参数变化对控制效果的影响,文章基于Matlab/Simulink软件中搭建燃料电池发动机空气供应系统仿真模型,进行仿真分析。
3.1 阶数n对控制效果的影响
为探究阶数n对控制效果的影响,给定一组阶跃工况,设定截止频率ωc=3,夹角θ=60°,分别取阶数n=2、3、4进行仿真分析,系统响应曲线如图5和6所示。

图5 空气流量回路响应
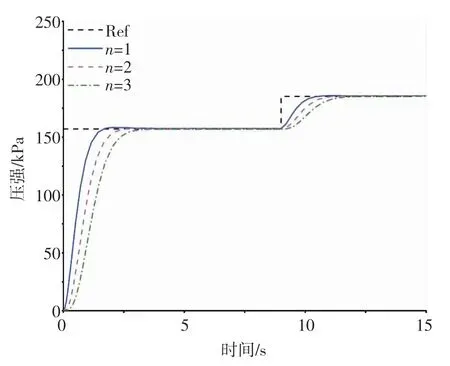
图6 压强回路响应
通过仿真可以看到,随着阶数n增大,系统的响应速度减慢,会增加上升时间,但超调量会随n的增加而减小。
3.2 截止频率ωc对控制效果的影响分析
为探究截止频率ωc对控制效果的影响,给定一组阶跃工况,设定阶数n=2,夹角θ=60°,分别取阶数ωc=1、2、3进行仿真分析,系统响应曲线如图7和8所示。

图7 空气流量回路响应
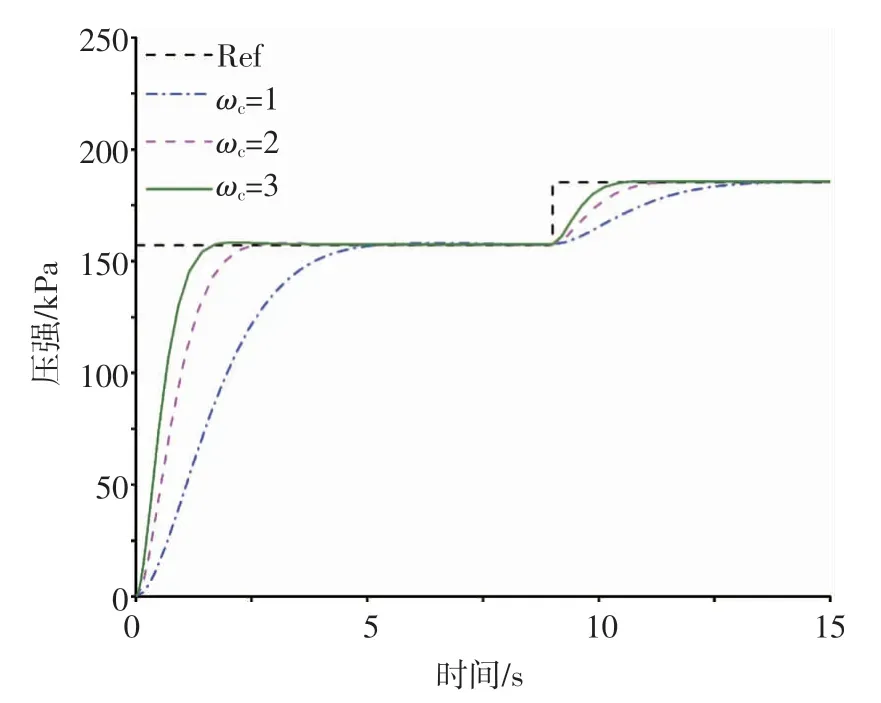
图8 压强回路响应
通过仿真可以看到,随着截止频率ωc增大,系统的响应速度加快,超调量没有变化。这是由于夹角θ不变,阻尼比ζ=sinθ不变,所以超调量不会发生变化,但是分析可知系统的抗干扰能力会减弱。
4 结论
1)改进型Butterworth滤波器的内模解耦控制策略较传统一型滤波器的内模解耦控制策略具有可调节参数多的优点,能够满足更多的控制效果需求。对于重卡用大功率燃料电池发动机空气供应系统的解耦控制效果非常理想,可以实现空气流量回路和压强回路的独立控制;
2)改进型Butterworth滤波器中,保持截止频率ωc和夹角θ不变,阶数n增大会使系统的响应速度减慢,但可以减小超调量数值;
3)改进型Butterworth滤波器中,保持阶数n和夹角θ不变,截止频率ωc增大会使系统的响应速度加快,降低系统的稳定性。

