基于性能的屈曲约束支撑与黏滞阻尼器组合减震结构设计方法

吴克川 陶忠 潘文 王林

摘 要：基于结构自振周期及阻尼比变化对结构地震作用的影响规律，推导屈曲约束支撑（BRB）与黏滞阻尼器（VD）组合减震结构单自由度体系位移降低率及地震剪力降低率计算公式，绘制组合减震结构在目标位移降低率及目标剪力降低率下的减震性能曲线，提出基于性能的组合消能减震设计方法，采用工程算例验证该设计方法的有效性，并提出组合减震设计方法在多自由度体系中的简化应用模式。结果表明：当目标位移降低率及目标剪力降低率确定时，结构存在唯一减震性能点，合理设计下，组合减震结构可同时取得较好的位移及地震剪力减震控制效果，用该设计方法得到的算例结构实现了设定的减震目标，质量和刚度沿高度均匀分布的多自由度体系组合减震设计可采用该基于一阶振型的简化应用方法。

关键词：屈曲约束支撑;黏滞阻尼器;组合减震;位移降低率;剪力降低率

中图分类号：TU352.1;TU311.41 文献标志码：A 文章编号：2096-6717（2021）03-0083-10

Abstract： Based on the influence rule of the structural natural vibration period and the damping ratio on the seismic excitation of the structure， the calculation formula of displacement reduction rate and seismic shear reduction rate of SDOF system of the combined damping structure with BRB and VD are derived and the damping performance curve of combined energy dissipation structure under target displacement reduction rate and target shear reduction rate is established. In addition， the performance-based combined energy dissipation design method is proposed and the validity is verified with a practical engineering example. The simplified application mode of the combined energy dissipation design method in multi-degree-of-freedom system is proposed. The results show that there exists unique performance point under the case that the target displacement reduction rate and target shear reduction rate are determined， and the combined damping structure could achieve excellent displacement response and seismic shear reduction control effects if designed reasonably. The calculation example structure designed according to the design method achieves the expected damping target. The simplified application method based on the first-order mode can be used for the combined seismic design of multi degree of freedom system with uniformly distributed mass and stiffness along the height.

Keywords：buckling restrained brace; viscous damper; combined energy dissipation; displacement reduction rate; shear reduction rate

消能減震技术[1]是指在建筑结构的特定部位设置消能装置，通过该装置吸收、耗散输入结构的振动能量，从而减小结构的地震反应。消能装置根据不同的工作原理可分为位移型消能器和速度型消能器[2]，其中，屈曲约束支撑（buckling restrained brace，BRB）与黏滞阻尼器（viscous damper，VD）分别为位移型消能器和速度型消能器的典型代表。目前，工程中应用消能减震技术时，大多采用单一类型阻尼器进行结构抗震设计[3-6]，而对组合使用BRB和VD减震技术的研究则较少。

陈斯聪等[7]对采用BRB+VD、BRB及VD减震方案结构的抗震性能进行了对比，并提出逐步布置阻尼器的减震设计方法，该方法通过调整阻尼器的数量及布置位置实现减震目标;吴宏磊等[8]基于性能化设计理念，提出组合消能减震技术在超高层建筑中的应用与设计，并通过一超高层建筑应用案例验证组合减震技术的有效性;兰树伟等[9]通过大量的分析计算，得到了特定设防烈度与场地条件下BRB和VD的匹配关系曲线;赵昕等[10]总结了BRB和VD的基本性能，提出了附加阻尼虚拟VD模型，并分析BRB的各种应力状态，并基于此进行BRB布置，进而提出了一种实用的混合减振设计方法。

以上研究均表明，在位移减震控制效果方面，BRB表现更好，而VD通过增加结构阻尼则能有效减小结构的地震剪力，二者组合使用可同时取得较好的位移及地震剪力控制效果。笔者基于结构自振周期及阻尼比变化对反应谱曲线的影响规律，推导BRB与VD组合减震结构单自由度体系位移降低率及地震剪力降低率计算公式，绘制组合消能减震结构的减震性能曲线，提出基于性能的组合消能减震设计方法，采用工程算例验证该设计方法的有效性，并给出了组合减震设计方法在多自由度体系中的简化应用模式。

1 组合减震结构位移降低率计算式

由地震反应谱理论可知[11]，周期在不同范围内变化时对结构地震力及位移影响的差异较大，因此，须掌握框架结构自振周期的分布规律。研究结果表明[12-13]：框架结构自振周期主要位于规范反应谱的曲线下降段，即Tg到5Tg范围内，笔者将基于该周期范围进行组合减震结构位移降低率及地震剪力降低率计算公式的推导。

《建筑抗震设计规范（GB 50011—2010）》[14]（简称《抗规》）规定建筑结构采用“两阶段，三水准”的抗震設计方法，即结构采用多遇地震作用下的地震内力进行承载能力设计，并验算其抗震性能指标，因此，笔者针对结构在多遇地震作用下的性能目标展开研究。设非减震结构（未设置消能器）的质量为m，抗侧刚度为Kf，阻尼比为ξ，自振周期为T;组合减震结构中BRB提供的附加刚度为ΔK，VD提供的附加阻尼比为ξa，结构自振周期为Te，消能器及其连接部件的质量为Δm，BRB与VD组合减震结构单自由度体系计算简图见图1。

非减震结构及组合减震结构的自振周期为

图2为非减震结构及组合减震结构自振周期关系曲线。从图中可以看出，两结构自振周期关系随消能器附加刚度及附加质量的增加呈非线性变化，且受消能器附加刚度的影响更为显著，这说明减震结构较非减震结构在动力特性上有较大改变，即结构的地震反应有较大变化。

设非减震结构单自由度体系在地震作用下的位移为x1，相应的等效地震内力为V1，设置消能器后的组合减震结构单自由度体系的位移为x2，相应的等效地震内力为V2，则有

采用振型分解反应谱法计算非减震结构及组合减震结构地震内力V1及V2，钢筋混凝土框架结构自振周期主要位于规范反应谱的曲线下降段，地震影响系数α采用该周期范围内公式进行计算，即

式中：Tg为建筑所在场地特征周期;η2及η2e为非减震结构及组合减震结构的阻尼调整系数;αmax为地震影响系数最大值;g为重力加速度;非减震结构阻尼调整系数η2取1，衰减指数γ取0.9;组合减震结构阻尼调整系数η2e及衰减指数γe分别按式（9）、式（10）计算。

将式（3）、式（9）、式（10）代入式（8），并联立求解式（5）、式（6）、式（7），得

式（11）即为组合消能减震结构在特定目标位移下所需BRB提供的附加刚度及VD提供的附加阻尼比组合关系式，其中，μx为组合减震结构目标位移x2与非减震结构位移x1之比（μx=x2/x1）。当附加阻尼比ξa=0时，式（11）转化为BRB减震结构在目标位移下的刚度需求方程;当刚度比μk=0时，式（11）转化为VD减震结构在目标位移下的阻尼需求方程;当BRB设计为多遇地震屈服时，式（11）中的附加阻尼需求为BRB及VD提供附加阻尼之和，附加刚度需求为BRB屈服后提供的等效刚度（割线刚度）。

图3为位移比μx不同取值下，刚度比μk与附加阻尼比ξa间的组合关系曲线，从图中可以看出：当结构目标位降低率一定时（即位移比μx确定时），随着VD提供附加阻尼比的增加，结构对BRB提供刚度的需求随之降低，且两者呈非线性变化关系;当VD提供的附加阻尼比较大时，随着附加阻尼比的增加，所需BRB附加刚度的变化趋于平缓;当结构附加阻尼比或附加刚度确定后，可通过图中曲线确定相应目标位移下结构所需的附加刚度或附加阻尼比;在考虑《抗规》对消能减震结构附加阻尼比上限值规定的情况下，难以通过仅附加阻尼比实现结构较小的目标位移值（例如μx=0.5时）。

2 组合减震结构剪力降低率计算式

在组合减震结构中，由于BRB为结构提供附加刚度，使结构自振周期减小，从而在一定程度上增加结构地震剪力[15-17]，VD则会增大结构阻尼，提高结构耗能能力，一定程度上减小结构地震剪力[18-20]，这一增一降作用的结果可能使结构的地震剪力增加或降低，地震剪力的最终增减结果受到结构附加刚度及附加阻尼比组合关系的影响，合理设计下，组合减震结构可同时取得较好的位移及地震剪力控制效果。将式（7）除以式（8），得

将式（9）、式（10）代入式（12）并化简得

式（13）即为组合消能减震结构在特定目标地震剪力降低率下所需BRB提供附加刚度及VD提供附加阻尼比组合关系式，其中，μv为组合减震结构地震剪力V2与非减震结构地震剪力V1之比（μv=V2/V1），当BRB设计为多遇地震屈服时，结构附加阻尼需求同样为BRB及VD提供附加阻尼之和，附加刚度需求同样为BRB屈服后提供的等效刚度;当刚度比μk=0时，式（13）转化为VD减震结构在目标剪力降低率下的阻尼需求方程。

图4为剪力比μv不同取值下，刚度比μk与附加阻尼比ξa间的组合关系曲线。从图4可以看出：当结构目标剪力降低率一定时（即剪力比μv确定时），随着刚度比μk的增大，结构需求的附加阻尼比ξa随之增加;附加阻尼比一定时，结构剪力降低率随刚度比μk的增大而减小;当刚度比μk过大时，即BRB为结构提供较大附加刚度时，在考虑《抗规》对消能减震结构附加阻尼比上限值规定的情况下，无法通过VD提供的附加阻尼比实现结构地震剪力的降低。

3 组合减震结构减震性能曲线

采用设置BRB及VD组合减震结构的位移、剪力与非减震结构的位移、剪力之比μx、μv来表示结构的地震反应降低程度，将μx及μv表示为附加刚度ΔK及附加阻尼比ξa的连续函数（式（11）及式（13）），定义该函数组成的方程组为组合减震结构的减震性能曲线，该曲线的绘制步骤为：

1）按常规抗震设计方法设计非减震结构，并计算出非减震结构单自由度体系自振周期T，设定结构的目标位移比（反映位移降低程度）及目标剪力比（反映地震剪力降低程度）;

2）根据式（11）计算不同μx取值下结构所需附加刚度ΔK及附加阻尼比ξa的组合值;

3）根据式（13）计算不同μv取值下结构所需附加刚度ΔK及附加阻尼比ξa的组合值;

4）第2步和第3步计算得到的组合值的交集即为减震性能点。

重复步骤1）～步骤4），可求得位移比μx及剪力比μv不同取值下减震性能点组成的减震性能曲线，如图5所示。

从图5可以看出，当结构位移降低率及剪力降低率确定时，可求得唯一的减震性能点（图中实线与虚线交点），继而可求解出相应减震目標下所需的附加刚度与附加阻尼比，合理设计下，组合减震结构可同时取得较好的位移及地震剪力减震控制效果。

4 组合消能减震设计方法与步骤

利用减震性能曲线进行结构的组合减震设计，步骤为：

1）按常规抗震设计方法设计非减震结构，并计算非减震结构的基本参数，包括结构自振周期T、抗侧刚度Kf、场地特征周期Tg等，设定结构的位移降低目标及地震剪力降低目标（相当于设定目标位移比及目标剪力比）。

2）绘制目标位移比及目标剪力比下的减震性能曲线，求解出两曲线交点的坐标值，该交点坐标值即为目标位移降低率及目标剪力降低率下的附加阻尼比需求及附加刚度需求。

3）根据附加刚度需求及附加阻尼比需求确定BRB数量及VD数量，并进行产品选型设计，当BRB的性能目标设计为多遇地震屈服时，应特别注意BRB的产品参数设计与性能目标的一致性。

4）采用有限元软件建立组合减震分析模型，通过反应谱等效线性化分析或时程分析验证是否达到减震目标。

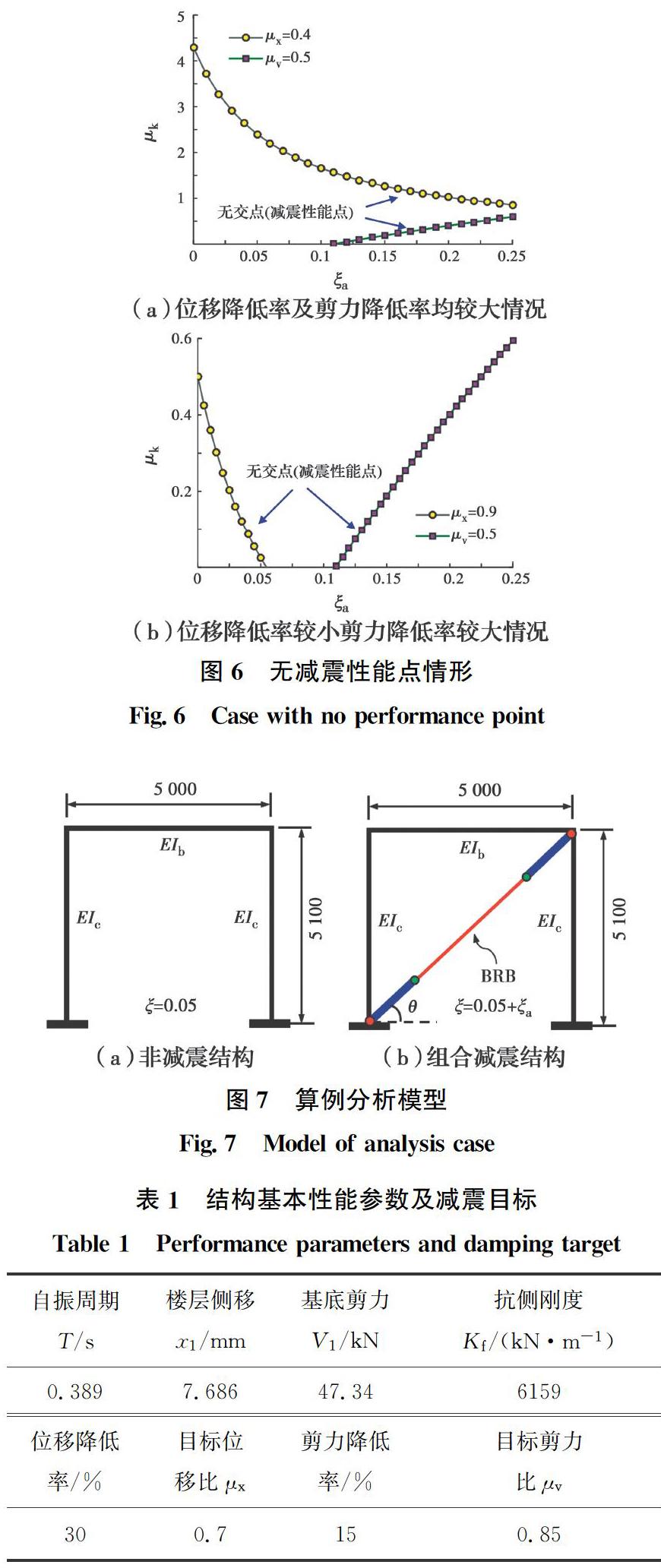
在设计过程中，应注意合理设定结构的减震目标，即设定合理的位移降低率及地震剪力降低率，避免出现位移降低率及地震剪力减低率均较大以及位移降低率较小而地震剪力减低率较大的情况，这是考虑到此情况下可能出现减震性能曲线无交点的情形，见图6，即无法通过合理的组合减震设计同时实现位移减震目标及地震剪力减震目标。根据图5中减震性能点的分布规律，μx的建议取值范围为0.5～0.8，μv的建议取值范围为0.7～0.9。

5 算例验证分析

5.1 算例模型概况

某单层钢筋混凝土框架结构如图7（a）所示，梁截面尺寸为200 mm×400 mm，柱截面尺寸为300 mm×300 mm，梁、柱混凝土强度等级均为C30，层高为5.1 m，跨度为5 m，楼面恒载为5 kN/m2，活载为2 kN/m2，结构抗震设防烈度为8度（0.3g），设计地震分组为第二组，场地类别为I0类，场地特征周期Tg=0.25 s。结构基本性能参数及减震目标见表1，基于设定的减震目标（位移降低目标及地震剪力降目标）采用BRB及VD组合减震方案进行结构消能减震设计。

5.2 附加刚度ΔK及附加阻尼比 ξa计算

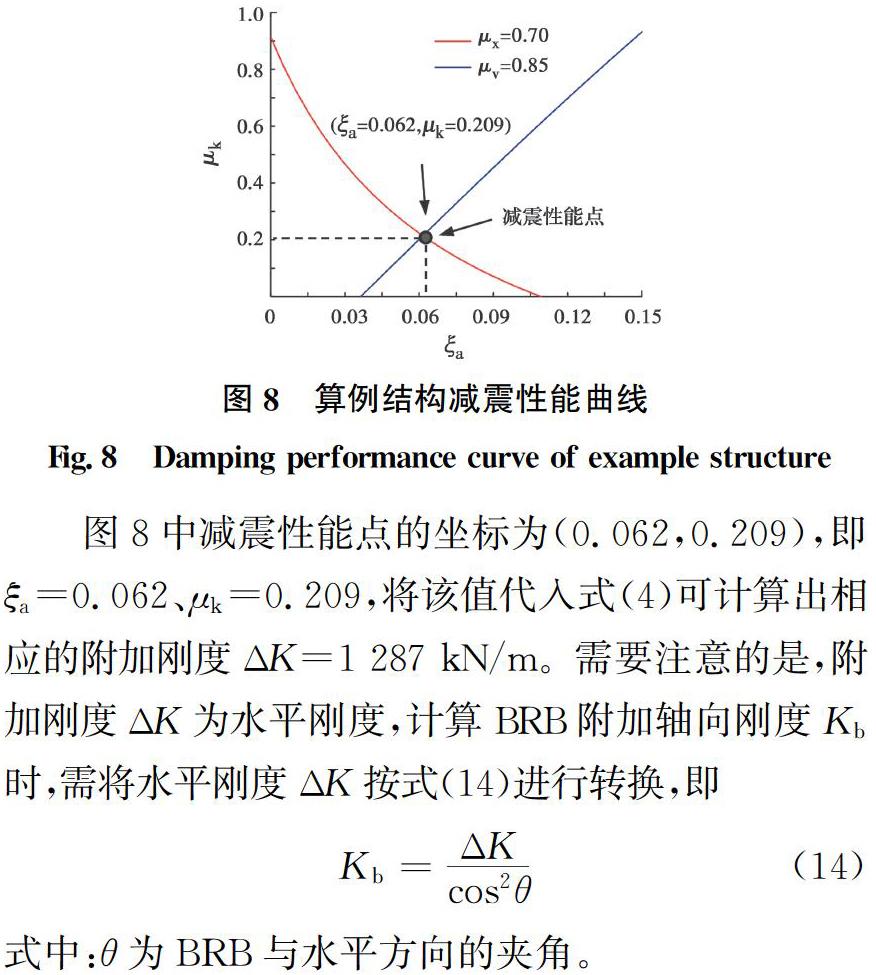
将表1中结构基本参数代入式（11）及式（13）中，计算出目标位移降低率及目标剪力降低率下结构所需附加刚度ΔK及附加阻尼比ξa的组合值，并将该组合值绘制成减震性能曲线，如图8所示，两曲线交点（减震性能点）坐标值即为所需附加刚度及附加阻尼比值。

图8中减震性能点的坐标为（0.062，0.209），即ξa=0.062、μk=0.209，将该值代入式（4）可计算出相应的附加刚度ΔK=1 287 kN/m。需要注意的是，附加刚度ΔK为水平刚度，计算BRB附加轴向刚度Kb时，需将水平刚度ΔK按式（14）进行转换，即

式中：θ为BRB与水平方向的夹角。

5.3 有限元验证分析

为验证算例模型采用该方法计算出的附加刚度及附加阻尼比能否实现结构的位移减震目标及地震剪力减震目标，采用SAP2000有限元软件对算例模型进行验证分析，梁、柱构件采用框架单元模拟，BRB采用塑性连接单元模拟，VD提供的附加阻尼作用通过修改结构自身的阻尼比模拟，有限元分析模型见图9。仅以X向为例进行分析说明，其中，结构所需BRB附加的轴向刚度Kb=2 627 kN/m，所需VD附加的阻尼比ξa=0.062，即结构的总阻尼比ξ=0.112。

采用符合《抗规》要求的5条天然波及2条人工波进行时程分析，对比非减震结构及组合减震结构的楼层侧移及地震剪力，并计算结构位移降低率及剪力降低率，从而验证设计方法的有效性。表2为结构剪力比、位移比实际计算值与目标值的对比。从表2可以看出，各地震波工况下结构剪力比、位移比平均计算值分别为0.844、0.693，与目标值间的误差分别为0.76%与1.04%，反应谱工况下结构剪力比、位移比计算值分别为0.862、0.716，与目标值间的误差分别为1.43%与2.32%，实现了设定的位移减震目标及地震剪力减震目标，也验证了该组合消能减震设计方法的有效性。

6 多自由度体系中的简化应用

6.1 基于一阶振型的简化应用

为将该计算公式应用于多自由度框架体系，对多自由度框架体系参数进行简化：1）将多自由度框架体系视为一悬臂构件，如图10所示;2）多自由度体系位移降低率采用结构顶点最大位移降低率表示;3）多自由度体系地震剪力降低率采用结构底部剪力降低率表示;4）式（11）及式（13）中的基本自振周期T采用结构相应主轴方向上的一阶自振周期，刚度Kf采用结构的整体抗侧刚度，质量m采用结构的总质量。

按照该简化方法，计算出多自由度体系在目标位移降低率及目标地震剪力降低率下的整体附加刚度需求及附加阻尼比需求。值得注意的是，该附加刚度需求及附加阻尼比需求为多自由度体系的性能总需求，须将附加刚度及附加阻尼按楼层进行分配，BRB提供的附加刚度可初步按结构楼层刚度进行分配，VD提供的附加阻尼可初步沿楼层高度方向进行均匀分配，最终，通过对组合减震结构进行非线性时程分析验证是否实现设定的减震目标。

6.2 工程实例分析

以某框架结构为工程案例，该结构总高度为23.3 m，共6层，底层层高为5 m，标准层层高为3.9 m，结构抗震设防烈度为8度，基本地震加速度为0.3g，场地特征周期Tg=0.45 s，结构固有阻尼比为5%，计算模型如图11（a）所示。

6.2.1 非减震结构分析

采用SAP2000软件建立分析模型，其中框架梁柱构件采用杆单元，楼板采用壳单元，并在梁和板上施加荷载，通过反应谱分析得到结构的各项性能参数如表3所示，并设定结构的位移降低目标及底部剪力降低目标。

6.2.2 BRB及VD参数设计

按照简化处理思路，将表3中结构的基本参数代入式（11）及式（13）中求解减震目标下结构所需整体附加刚度ΔK及附加阻尼比ξa，如图12所示。从图12可以看出，结构X向、Y向所需附加刚度分别为ΔKx=402 618 kN/m、ΔKy=461 985 kN/m，所需附加阻尼比分别为ξax=9.5%、ξay=9.2%。由于该结构总层数为6层，其中，1～4层的层间位移角较大，因此，考虑将阻尼器（BRB、VD）布置在结构的1～4层，将BRB提供的附加刚度按结构楼层刚度进行分配，VD提供的附加阻尼沿楼层高度方向均匀分配，即在布置阻尼器的楼层中，所用VD的数量和参数均相同，根据计算出的结构性能需求（附加刚度需求和附加阻尼比需求）进行BRB、VD的参数设计及选型，最终得到减震目标下的BRB及VD参数见表4及表5。

6.2.3 时程验证分析

采用SAP2000软件建立组合减震结构分析模型，并根据表4及表5中結果输入阻尼器参数，其中BRB采用Bouc-Wen单元模拟，VD采用Damper单元模拟，按照简化方法进行阻尼器布置，见图13，组合减震结构有限元分析模型见图12（b）。选择符合《抗规》要求的5条天然波以及2条人工波进行时程分析，各地震波的峰值加速度调整为110 cm/s2，其反应谱曲线与规范设计反应谱的对比见图14。通过时程分析计算结构的顶点位移降低率及底部剪力降低率，并与减震目标进行对比，从而验证文中提出的多自由度体系基于一阶振型的简化应用方法的有效性与正确性。

图15为混合减震结构与非减震结构在各地震波作用下的楼层剪力平均值及楼层侧移平均值的对比，其中，组合减震结构与非减震结构X方向的底部剪力分别为5 152、6 179 kN，Y方向的底部剪力分别为5 067、6 348 kN，组合减震结构与非减震结构X方向的顶点位移分别26.26、50.08 mm;Y方向的顶点位移分别28.09、47.62 mm。根据以上数据可计算得到结构在X方向及Y方向的底部剪力降低率分别为16.62%、20.18%，X向及Y向的顶点位移降低率分别为47.56%、41.01%，均实现了设定的位移减震目标及地震剪力减震目标，这也在一定程度上说明了提出的多自由度体系基于一阶振型的简化应用方法的有效性。

7 结论

对框架结构自振周期进行统计分析，通过推导组合减震结构位移降低率及地震剪力降低率计算公式，绘制了组合减震结构的减震性能曲线，提出基于性能的组合减震设计方法，得到以下结论：

1）当结构目标位移降低率确定时，随着VD提供附加阻尼比的增加，结构对BRB提供刚度的需求随之降低。

2）考虑《抗规》对消能减震结构附加阻尼比上限值规定的情况下，难以通过仅附加阻尼比实现结构较大的位移降低率，且当刚度比μk过大时，无法通过提高附加阻尼比实现结构地震剪力的降低。

3）当结构目标剪力降低率确定时，随着刚度比μk的增大，结构需求的附加阻尼比ξa随之增加;附加阻尼比一定时，结构剪力降低率随刚度比μk的增大而减小。

4）当目标位移降低率及目标剪力降低率确定时，结构存在唯一的减震性能点，合理设计下，组合减震结构可同时取得较好的位移及地震剪力减震控制效果。

5）工程案列分析结果表明：文中提出的组合减震设计方法可采用基于一阶振型的简化方式应用于多自由度体系的消能减震设计。

以上结论适用于自振周期处于规范反应谱曲线下降段、质量和刚度沿高度均匀分布、以剪切变形为主，且总阻尼比不超过30%的消能减震结构，其他周期范围内的结构可参考该思路进行推导。

参考文献：

[1] 周锡元， 阎维明， 杨润林. 建筑结构的隔震、减振和振动控制[J]. 建筑结构学报， 2002， 23（2）： 2-12，26.

ZHOU X Y， YAN W M， YANG R L. Seismic base isolation， energy dissipation and vibration control of building structures [J]. Journal of Building Structures， 2002， 23（2）： 2-12，26. （in Chinese）

[2] 建筑消能减震技术规程： JGJ 297—2013 [S]. 北京： 建筑工业出版社， 2013.

Technical specification for seismic energy dissipation of buildings： JGJ 297-2013 [S]. Beijing： China Architecture & Building Press， 2013. （in Chinese）

[3] 景铭， 戴君武， 刘永彬. 高层剪力墙结构消能连梁设计案例分析及几个问题的讨论[J]. 地震工程与工程振动， 2017， 37（6）： 79-89.

JING M， DAI J W， LIU Y B. Case analysis and discussion on the designing of energy-dissipative coupling beams in high-rise shear wall structures [J]. Earthquake Engineering and Engineering Dynamics， 2017， 37（6）： 79-89. （in Chinese）

[4] 高杰， 徐自国， 任重翠， 等. 北京市轨道交通指挥中心（二期）屈曲约束支撑设计及动力弹塑性分析[J]. 建筑结构学报， 2014， 35（1）： 56-62.

GAO J， XU Z G， REN C C， et al. Beijing Rail Transit Command Center（Phase Ⅱ） energy dissipation technology and dynamic elasto-plastic analysis [J]. Journal of Building Structures， 2014， 35（1）： 56-62. （in Chinese）

[5] 翁大根， 张超， 吕西林， 等. 附加黏滞阻尼器减震结构实用设计方法研究[J]. 振动与冲击， 2012， 31（21）： 80-88.

WENG D G， ZHANG C， LV X L， et al. Practical design procedure for a energy-dissipated structure with viscous dampers [J]. Journal of Vibration and Shock， 2012， 31（21）： 80-88. （in Chinese）

[6] 吳宏磊， 陈长嘉， 丁洁民， 等. 黏滞阻尼器在超高层建筑中的应用研究[J]. 建筑结构学报， 2016， 37（Sup1）： 39-47.

WU H L， CHEN C J， DING J M， et al. Application research of viscous damper in a super high-rise building [J]. Journal of Building Structures， 2016， 37（Sup1）： 39-47. （in Chinese）

[7] 陈斯聪， 周云. BRB+VD消能减震结构体系分析研究[J]. 建筑结构， 2016， 46（11）： 85-90.

CHEN S C， ZHOU Y. Analysis and research of BRB+ VD energy dissipation system [J]. Building Structure， 2016， 46（11）： 85-90. （in Chinese）

[8] 吴宏磊， 丁洁民， 刘博. 超高层建筑基于性能的组合消能减震结构设计及其应用[J]. 建筑结构学报， 2020， 41（3）： 14-24.

WU H L， DING J M， LIU B. Design and application of performance-based hybrid damping structures for super high-rise buildings [J]. Journal of Building Structures， 2020， 41（3）： 14-24. （in Chinese）

[9] 兰树伟， 周东华， 双超. 屈曲约束支撑与黏滞阻尼器联合减震设计研究[J]. 四川建筑科学研究， 2018， 44（6）： 21-26.

LAN S W， ZHOU D H， SHUANG C. Research on energy-dissipated design of buckling restrained braces and viscous dampers [J]. Sichuan Building Science， 2018， 44（6）： 21-26. （in Chinese）

[10] 赵昕， 杜冰洁， 李浩. 超高层建筑黏滞阻尼器及屈曲约束支撑混合减振结构系统集成优化设计[J]. 建筑结构学报， 2020， 41（3）：25-35.

ZHAO X， DU B J， LI H. Integrated optimization design of hybrid vibration damping structure system of viscous damper and buckling restrained brace for super high-rise buildings [J].Journal of Building Structures， 2020， 41（3）：25-35. （in Chinese）

[11] 林新阳， 周福霖. 消能减震的基本原理和实际应用[J]. 世界地震工程， 2002， 18（3）： 48-51.

LIN X Y， ZHOU F L. Theory and application of energy dissipation-seismic reduction technology [J]. World Information on Earthquake Engineering， 2002， 18（3）： 48-51. （in Chinese）

[12] XING L L， ZHOU Y， AGUAGUIA M. Optimal vertical configuration of combined energy dissipation outriggers [J]. The Structural Design of Tall and Special Buildings， 2019， 28（4）： e1579.

[13] GAO Y Q， LIU W F. Statistical analysis of fundamental periods of frame-shear wall structures [J]. Applied Mechanics and Materials， 2012， 174-177： 2071-2078.

[14] 建筑抗震設计规范： GB 50011—2010 [S]. 北京： 中国建筑工业出版社， 2010.

Code for seismic design of buildings： GB 50011—2010 [S]. Beijing： China Architecture & Building Press， 2010. （in Chinese）

[15] CHUANG M C， TSAI K C， LIN P C， et al. Critical limit states in seismic buckling-restrained brace and connection designs [J]. Earthquake Engineering & Structural Dynamics， 2015， 44（10）： 1559-1579.

[16] RYU J， KO H J， OH J， et al. Experimental evaluation of steel cable-pulley-bearing complex damping systems with silicone viscous damper [J]. Journal of Korean Society of Steel Construction， 2020， 32（4）： 247-255.

[17] QU B， LIU X F， HOU H T， et al. Testing of buckling-restrained braces with replaceable steel angle fuses [J]. Journal of Structural Engineering， 2018， 144（3）： 04018001.

[18] LI Y， QU H， XIAO S， et al. Behavior of three-tube buckling-restrained brace with circumference pre-stress in core tube [J]. Steel and Composite Structures， 2019， 30（2）： 81-96.

[19] MAGAR PATIL H R， JANGID R S. Numerical study of seismic performance of steel moment-resisting frame with buckling-restrained brace and viscous fluid damper [J]. The IES Journal Part A： Civil & Structural Engineering， 2015， 8（3）： 165-174.

[20] CHEN L， DI F D， XU Y Y， et al. Multimode cable vibration control using a viscous-shear damper： Case studies on the Sutong Bridge [J]. Structural Control and Health Monitoring， 2020， 27（6）： e2536.

（编辑 章润红）