基于卫星反演的有效波高研究

段凡平

摘 要：在很多非洲国家，波浪要素等水文资料的缺失是制约港口工程设计与施工的最主要因素之一。本文以喀麦隆克里比深水港项目为实例，在研究海域没有实测资料的情况下，以卫星反演测波理论为基础，推算深水波有效波高。为本项目设计与施工提供了科学的研究依据，亦为类似大型港口项目提供有效参考和经验思路。

关键词：港口;卫星反演测波;高度计法;有效波高

中图分类号：U65          文献标识码：A            文章编号：1006—7973（2021）03-0067-04

1绪论

近年来，随着习主席“一带一路”倡议引领，在中非合作论坛“八大行动”舉措的推进下，中资承包商在非洲国家或地区承建了一大批基础设施工程，改善了当地基础设施状态，提高了当地人民的生活水平，形成中非合作互利共赢的新局面，喀麦隆克里比深水港便是典型项目之一。

由于喀麦隆经济及技术发展相对落后，当地沿海未建有水文观测站，工程海域缺乏实测水文数据及波浪条件。而卫星反演测波为先进的技术手段，本文基于卫星反演测波理论，研究确定工程海域深水波有效波高，为项目的设计及施工提供依据。

2工程背景

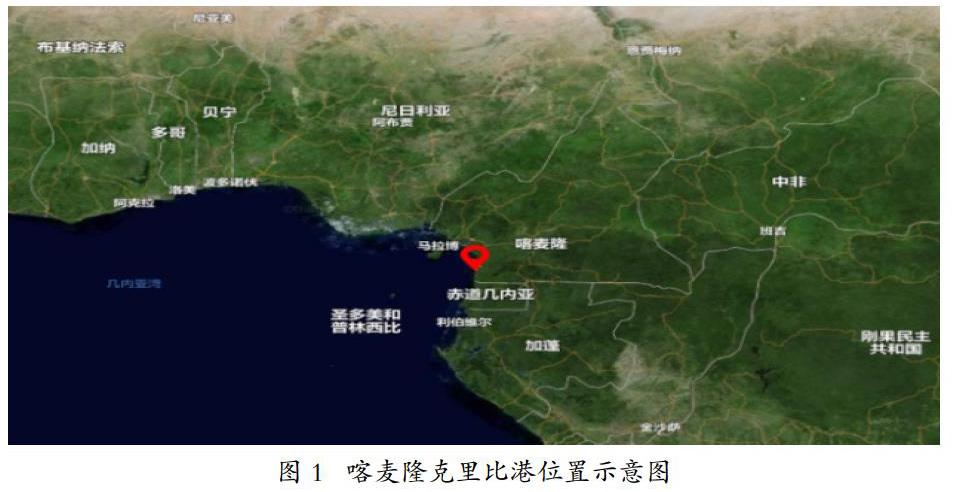
本文研究工程位于喀麦隆沿海城市克里比市，纬度02°43′N，经度 09°50′E，毗邻西非几内亚湾，见图1中红点标注。项目分为两期，一期为一个集装箱泊位和一个多用途泊位，二期为两个集装箱泊位。

根据现有有限的资料统计分析，西非几内亚湾海域除了被普遍认为存在短周期风浪、长周期涌浪外，还存在因极端天气下，排列成带状雷暴群的飑线[1]（见图2中红线）天气产生的飑线浪，波浪条件较复杂。而波浪要素是防波堤结构设计、码头结构设计、码头附属设施设计、港内泊稳条件计算及施工期临时设施和施工条件确定的重要因素。因此，在无实测资料的情况下，采取科学有效的技术方法确定深水波浪要素是本文项目的重中之重。

3卫星反演有效波高

3.1 卫星反演测波原理

最近二十年来，随着卫星传感器技术的日趋成熟，各个国家发射了多颗海洋卫星，其携带的传感器（高度计，合成孔径雷达，微波散射计，辐射计等），可以实现对海洋表面风场、盐度、有效波高、海温、悬浮泥沙场的观测[2]。现阶段，有两种传感器高度计和合成孔径雷达可以用来观测波浪，介于成熟度和应用广泛程度考虑，本文采用高度计传感器数据[3]。

高度计的应用都基于三个基本观测量：①时间延迟-高度计发射脉冲到接收海面回波信号的时间间隔-从中获取海面高度的信息，并由此反演海洋重力场、海洋大地水准面、海洋潮波系统等;②海面回波波形的前沿斜率-从中可以获取海面有效波高的信息;③海面回波波形强度-从中获取海面风速的信息。

高度计测量海上有效波高的原理依赖于反射的雷达脉冲的形状和时间。高度计在轨道运行绕地球运动的过程中，会不断向海面发射电磁脉冲，到达地面的雷达波束通常直径为几公里，这样的分辨率是无法来描述波浪结构的。然而，反射回来的雷达波会由于波浪的存在而产生变形。利用反射雷达波变形的特征信息，可以得到海面的粗糙度，通过大量理论和实验的分析，建立粗糙度和波高之间的联系，就可以反演波高。

图3显示了分别携带海浪波峰和波谷信息的雷达脉冲返回传感器时刻的示意图。在轨的高度计会持续向海面发射电磁脉冲，如果海面平整光滑，那么反射回来的雷达波仍然是脉冲形式。如果海面有波浪存在，那么入射脉冲会首先在波峰处产生反射，当脉冲继续向下传播，会有越来越多的入射波被反射回去;当脉冲到达波谷的时候，所有的入射脉冲都会被反射[4]。因此，在有波浪存在的情况下，卫星雷达接收到的脉冲波型会由于波面的起伏而产生扭曲变形。波浪越大，反射脉冲波的持续时间越长，波形的扭曲变形越严重。

假定波面高度服从高斯分布，可以证明在窄谱条件下海表面的波高服从瑞利分布。假定波面高度服从高斯分布，雷达脉冲的有效脉冲持续时间T与海表面的有效波高Hs之间存在如下关系：

式中，

C----光速;

Tp----发射的脉冲持续时间，它是雷达设计中设定的已知参数;

Hs----有效波高;

T----反射的雷达脉冲持续有效时间;

根据高度计反射雷达脉冲的形状和时间首先确定有效脉冲持续时间T，然后依据上述公式可获取海表面的有效波高。

3.2卫星数据介绍

因卫星数据商业化的滞后性，本文收集了最新商业卫星数据自1991-2011年，21年多颗卫星高度计测波资料，详细清单见表1：

其中ERS系列卫星和Jason系列卫星在几内亚湾附近的轨迹详见图4。从图中还可以看出，Jason系列卫星轨距比较大，而ERS要密很多，这是由于前者的回归周期要比后者小很多。为了增加取样的个数，会取工程附近的一个矩形区域作为卫星数据的采样区，本文选取区域为：经度方向： 东经4-9度;纬度方向：北纬 0-4度。区域大小见图5中红框，其中四条轨道分别是Jason卫星的 Pass33、Pass122、Pass198、Pass211在本区域内的轨迹线。

3.3卫星数据前处理

卫星高度计是根据其发射的主动式雷达脉冲经过不同粗糙海面的反射所获得的回波信号的不同形状来遥测海面波高。雷达微波及其回波信号在大气介质的传播中，要受到电离层、平流层，尤其是大气层和海气界面的影响。而其影响程度在时间上和空间上都要发生很大的变化， 因此在使用之前要做一些预处理和资料的质量控制。

卫星高度计的资料产品在发布之前，根据雷达微波及其回波信号在大气介质的传播中所受到电离层、平流层、尤其是大气层和海气界面的影响， 进行了大量的常规校正， 在资料中做了许多的标记。在T/P 高度计资料中， 给出了22字节的长度来标记“ENVIRONMENTAL CORRECTION GROU P”，分别给出干对流层、湿对流层、平流层、逆温层的校正参数; 给出了30 字节的“FLAGS GROU P”来标记高度计的姿态、资料的质量。在GEOSAT 高度计资料中有16 字节的校正数据段， 用来对固体潮、海洋潮、干对流层、湿对流层、平流层等对微波信号的干扰进行校正;用2 字节来记录高度计的姿态。

高度计设计者尽管在高度计的硬件设计和软件反演中做了诸多考虑，但由于其传播环境的复杂性和多变性以及海气界面的影响，使得不少遥感资料严重偏离实际海面的“真值”。因此，高度计遥感波高资料的质量控制，无论对于其本身，还是对于各种海洋应用研究来说都是十分重要的、必不可少的。

提高高度计遥感波高资料质量的第一步，可以根据质量标志位“FLAGS”或“FLAG GROUP”中的信息对其进行甄别和处理。但是仅经过上述处理是远远不够的，资料中仍然有大量失真的“坏资料”。为了更有效地甄别和清除失真资料，必须对高度计测波资料进行物理机制方面的控制[5]。

除了上述在读取数据时进行的订正之外， 在实际应用前应进行严格的质量控制，采用的物理判据为：风速超过18m/s 的数据;靠近陆地、有海冰覆盖和受降雨影响的测量值。满足以上条件之一的数据，应予以删除。经过以上数据预处理，虽然可能去除了一些实际上有效的观测值， 但可以进一步提高和保证数据的精度。

3.4 反演有效波高

利用上述方法，对1991-2011年21年间卫星波高数据进行前处理后，整理得到共4926个平稳海况，有效波高的统计数据如下表2所示：

21年间的最大深水波有效波高为3.21米，反演的深水有效波高见图6。

常用的推算重现期对于数据极大值的采样分为年最大值法和峰值阈值法。峰值阈值法会把所有大于某一阈值的数据点，全部作为进行极值分布的采样点，但是较低数值的采样点与较高数值的采样点并非一定服从同一分布。基于此，本文采用年最大值法，提取21年间的卫星实测深水有效波高最大值，得到图7。

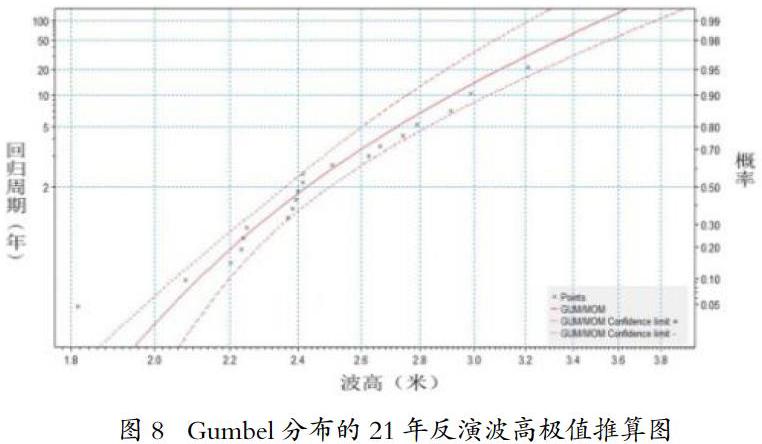
目前国内外常用的推算极值波高的概率分布有P-III曲线、Weibull、Gumbel、对数分布等[6]。其中对于卫星反演的波高，采用Gumbel分布较为合适。本文对以上四种分布都做了尝试，发现确实Gumbel分布的得出的结果最优，详见图8。

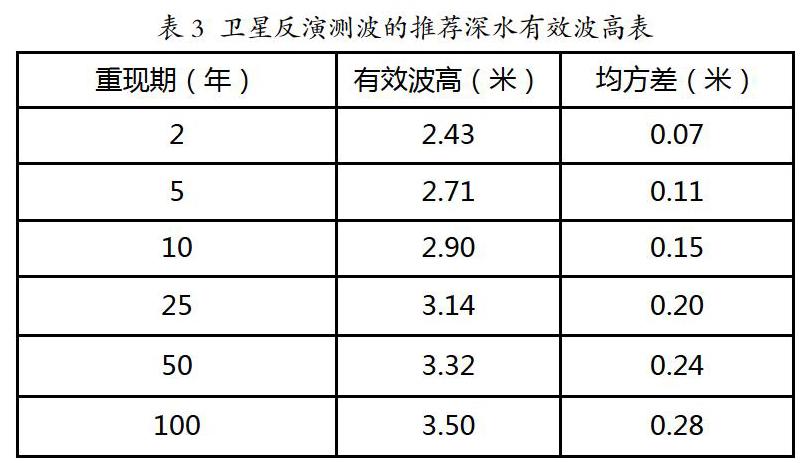
根据21年间卫星数据的年最大值，采用Gumbel分布，最终推算出的建议2年，5年，10年，25年，50年和100年一遇的重现期的深水有效波高见表3所示。

4结语

本文在喀麦隆克里比地区无实测水文资料的情况下，详细介绍了卫星反演測波技术原理，通过对获取的卫星数据进行前处理及推算，得到了项目海域不同重现期的建议深水有效波高，为项目后期的物数模试验及设计、施工提供了有力的依据与支撑。亦为“一带一路”沿线较不发达国家无实测波浪资料的大型港口项目提供了有效参考和经验思路。

参考文献：

[1] KOUASSI A A， YOROBA F， ASSAMOI P， et al. Numerical Study of a West African Squall Line Using a Regional Climate Model[J]. Atmospheric and Climate Sciences， 2012，2（1）.

[2] Wang Jiuke，Aouf Lotfi，Jia Yongjun，Zhang Youguang. Validation and Calibration of Significant Wave Height and Wind Speed Retrievals from HY2B Altimeter Based on Deep Learning[J]. Remote Sensing，2020，12（17）.

[3] 钱扬风，孙建.JASON-2卫星高度计波高数据同化对中国渤黄海海浪数值预报影响研究[J].海洋湖沼通报，2020（04）：14-22.

[4] 许安迪，陈学恩.基于卫星高度计数据的全球海洋潮汐特征分析[J].中国海洋大学学报（自然科学版），2021，51（01）：1-8.

[5] 韩树宗，王海龙，郭佩芳.利用卫星高度计资料进行多年一遇极值波高推算的方法研究[J].青岛海洋大学学报（自然科学版），2003（05）：657-664.

[6] Rituparna Chutia， D. Datta. Construction of a fuzzy probability space with Gumbel function， Gaussian function， derivative of Gaussian function and Weibull function[J]. Int. J. of Fuzzy Computation and Modelling，2016，2（1）.