刚柔耦合特种车辆越障行驶动力学分析及悬架优化*

刘欢 1 李韶华 1，† 张培强

（1.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，石家庄 050043）

（2.石家庄铁道大学机械工程学院，石家庄 050043）

前言

基于ADAMS等软件的虚拟样机技术发展，通过整车建模及动力学仿真可以使设计人员在设计之初就对车辆性能全面分析和优化，使之能缩短开发周期、降低成本［1］.特种车辆因其特殊性，经常行驶于具有障碍路面的越野环境中，因此研究特种车辆通过障碍路面时的动态性能，并设计优化方案，不仅可以提高车辆平顺性、减小人员健康隐患［2］，而且可以提高作战能力.

目前，对于车辆行驶平顺性的研究，正在从随机路面、匀速直线行驶工况扩展到凸台、凹坑、变速等越野极限工况；研究对象也从汽车本身扩展到特种车辆.董明明［3］建立了8×8越野车模型，利用遗传算法对悬架刚度和阻尼进行了匹配优化，有效提高了越野车辆的平顺性；秦伟［4］建立了某车载火箭炮车辆模型，对该车通过垂直路障、壕沟进行了计算，通过仿真分析研究了该车的越障能力；程康［5］建立了某越野车刚柔耦合模型，对该车平顺性进行了仿真分析评分评价，并研究了越野车通过垂直台阶、陡坡路面时的动力学性能；王钦龙［6］建立了某型6×6轮式越野车辆多刚体动力学模型，分析了其振动固有特性和频响特性，并利用多刚体动力学模型进行了随机路面匀速行驶的动力学仿真.谢润［7］建立了某火炮特种车辆，进行了不同随机路面工况下车辆和炮管发射时的动态性能研究.洪刘生［8］以改善某轻型越野车平顺性为目的，建立路面-车辆动力学模型，将响应面法、神经网络模型、克里格方法应用到近似建模中，应用多目标粒子群优化算法对悬架系统参数进行优化.但是以上研究主要关注车辆本身的动力学性能，对于炮管的振动冲击进行分析的文献，尚不多见.

本文利用ADAMS软件建立了具有双横臂独立悬架、柔性炮管的刚柔耦合特种车辆模型，并与带有刚性炮管的整车进行对比分析.考虑通过障碍的能力不同，计算了该整车模型通过凸台障碍路面的极限高度，并建立了不同参数的凸台障碍路面，研究了特种车辆的越障行驶动力学性能.最后通过悬架参数的优化，提高了整车在障碍路面下的平顺性.研究结果可为特种车辆研发提供理论依据.

1 特种车辆刚柔耦合模型的建立

利用ADAMS/Car软件建立特种车辆整车模型，考虑到建模过程的便捷性，充分利用样板模型进行修改.为提高整车模型的准确性，对弹性变形大的炮管进行柔性化处理.

1.1 双横臂独立悬架模型的建立

悬架是车身与轮胎之间力传递的桥梁，可以缓冲不平路面传给车架和车身的冲击力，减小由此引起的振动，保证车辆平顺行驶［9］.双横臂悬架具有横向刚度大，抗侧倾性能优异，抓地性能好.适合于运动速度快、重量大、行驶环境恶劣的军用特种车辆［8］.因此本文利用ADAMS软件中的双横臂独立悬架样板，根据拓扑结构依次进行硬点及方向、通讯器的修改匹配［10］.建立的双横臂悬架模板如图1所示，从左到右依次为前悬架、中悬架、后悬架.

图1 双横臂独立悬架Fig.1 Double wishbone independent suspension

1.2 柔性炮管的建立

在ADAMS/Flex中用有限元法处理柔性多体动力学，将柔性体用离散化的若干个单元的有限个节点自由度来表示物体的无限多个自由度.这些单元的弹性变形可近似用少量模态线性组合表示［11］.本文首先生成炮管.MNF中性文件，导入ADAMS/Car并替换刚性炮管，并利用BUISHING建立刚体、柔体之间的连接.

对于实际工程有意义的模态多为低频部分，因此选取炮管前20阶低频模态计算响应，并根据各阶模态质量、惯矩在总模态所占份额，将1-6阶刚性模态失效.最终用于计算分析的模态、频率如表1所示.

表1 被激活的炮管模态阶数与频率Table1 Modal order and frequency of the activated barrel

1.3 整车模型的建立

利用模板依次建立各个子系统，即可组装刚柔耦合整车模型，如图2所示.整车质量取为1.5×104kg，转动惯量取为Ixx：1.3×1010，Iyy：4.42×1010，Izz：3.72×1010（kg·mm2）.

图2 组装后的刚柔耦合整车模型Fig.2 Rigid-flexiblecoupled vehicleafter assembling

1.4 刚柔耦合建模对炮管响应的影响

考虑到特种车辆恶劣行驶环境，利用轮廓生成器（Road-Profile Generation）来生成了B级随机路面，如图3所示.

图3 B级随机路面的生成Fig.3 Generation of Class BRandom Pavement

为了进行对比，另外建立了带刚性炮管的整车模型.使刚性车和刚柔耦合整车分别以30km/h速度匀速通过前面生成的B级随机路面，得到两种炮管的炮口垂向和水平方向位移、速度、角速度，如图4所示.从图4可以看出：

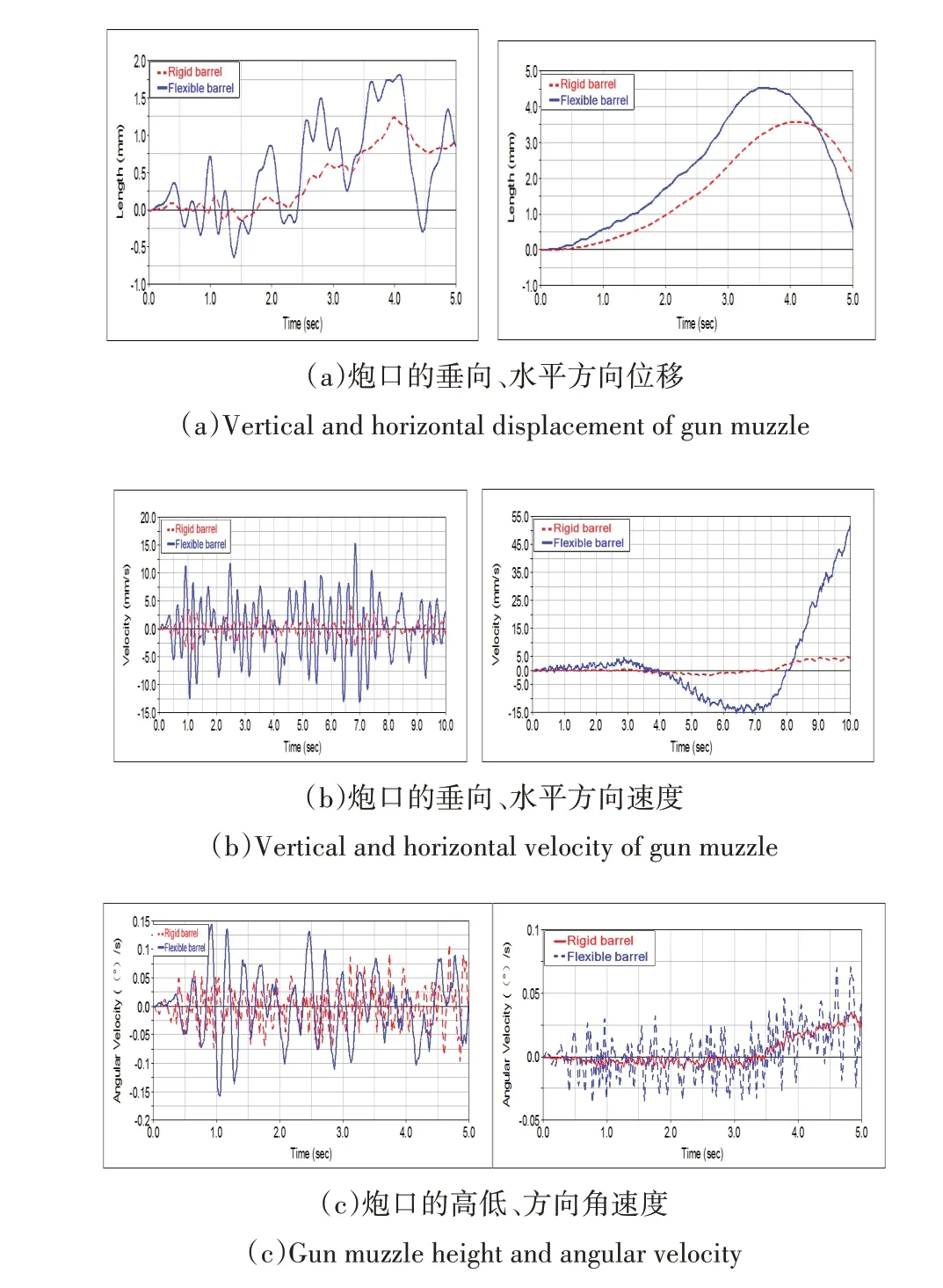
图4 刚、柔炮管响应曲线对比Fig.4 Comparison of Response Curves of Rigid and Flexible Gun Barrels

（1）在整个行驶过程中，炮口垂向位移、速度的幅值要小于炮口水平方向上位移、速度幅值.这是由于在随机路面工况下，左右轮受力不均匀，导致车身不稳定，进而传递给炮管.

（2）在整个行驶过程中，柔性炮管炮口垂向及方向上的位移、速度、角速度等参量较刚性炮管炮口的响应较明显，且波动相对于刚性炮管较剧烈.原因是柔性化炮管振动不仅受路面影响，而且柔性化炮管的离散单元在整个仿真过程中受自身弹性变形影响，而刚性炮管更多的是作为车身的部件，仅由路面状况决定.

（3）同工况下行驶时，柔性炮管的振动频率较大，且与刚性炮管振动频率成倍数关系.说明在分析炮管动态性能时，柔性化的模型对测试结果影响明显，炮管弹性变形不可忽视.

综上分析得出，炮管的弹性变形对炮口垂直方向参量（线位移、线速度、角速度）、炮口的水平方向参量（线位移、线速度、角速度）影响显著.因此带有柔性炮管的刚柔耦合整车在行驶中炮口的动态性能更符合实车动态性能，其建模精度更高.

2 障碍路面下整车的行驶动力学

车辆行驶时，对路面不平度的隔振特性，称为车辆的行驶平顺性.行驶在恶劣路面环境时，路面的不平会激起整车的振动［12］，振动达到一定程度时，会对车辆产生很大的冲击，不仅影响驾驶员的乘坐舒适性和射击时的精度，而且会缩短车辆的使用寿命.下面通过建立障碍路面来分析整车的动态响应.

2.1 垂直凸台障碍路面极限高度的确定

车辆超越垂直凸台障碍的能力主要取决其所能克服的垂直障碍的极限高度h.整车模型在前轮刚接触凸台障碍时的状态图和受力图，如图5、图6所示.

图5 前轮驶入时状态图Fig.5 Statediagram when thefront wheel drivesin

图6 前轮驶入时受力图Fig.6 Force diagramwhen thefront wheel drivesin

整车垂直方向、水平方向的力平衡方程式以及前轴的力矩平衡方程式：

其中，N1、N2分别为地面对前、后车轮的反作用力，uN1、uN2分别为前、后车轮与地面接触点处的推力，u取0.8，m为整车重量，α为前轮上的反作用力与水平面的夹角，h为垂直台阶的高度，h0为车重心到车轴平面的垂直距离，a为前轴至车重心的水平距离，r为车轮半径，l为前后车轴距.具体参数如表2所示.

表2 整车参数Table 2 Vehicle Parameters

由式（1）可解得h的极限高度为330mm.因此下面仿真试验时所建立的凸台障碍高度应在330mm以下.

2.2 通过凸台障碍路面时特种车辆动力学响应分析

通过凸台障碍路面时，如果车速过高，容易造成整车跳动和偏移，引起较大的测量误差，因此速度不宜过高.车辆以20km/h速度，双侧六轮通过高100mm垂直凸台时，整车和炮管的垂向加速度、侧向加速度、横摆角速度，如图7～图9所示.由图7可知，在行驶到3.5s时，整车开始接触垂直凸台障碍，此时整个系统的垂向加速度发生突变，整车质心垂向加速度突变为1.5g，炮管突变为2.5g，且在整个障碍路面冲击作用下，整车质心垂向加速度峰值为1.5g，炮管为4g，相差三倍多.这是由于柔性炮管的弹性变形，导致其垂向加速度大于整车质心垂向加速度.当通过凸台后，垂向加速度均能快速稳定下来.且从图8可知，在整个障碍路面行驶过程中，整车和炮管侧向加速度峰值仅为0.02g、0.05g，侧向加速度在障碍路面下均不大.说明整车在遇到障碍路面时受到的垂向冲击较大，但其行驶中仍具有较好的稳定性.

图7 垂向加速度Fig.Vertical acceleration

图8 侧向加速度Fig.Lateral acceleration

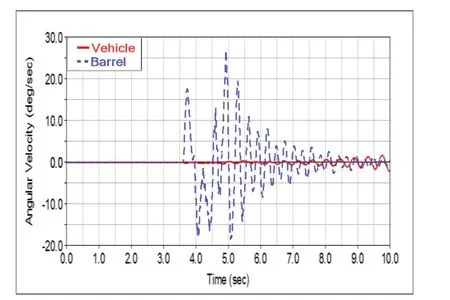
图9 横摆角速度Fig.Yaw rate

由图9可知，在驶入障碍路面时，炮管的横摆角速度无论是大小范围还是波动情况均明显大于整车质心，炮管的横摆角速度在此障碍路面行驶中的峰值为25deg/sec；在驶出障碍路面时，两者的横摆角速度均能够快速稳定下来.这是因为整车具有较好的越障能力，而炮管作为大长径比的弹性部件，其通过冲击路面时，横摆运动相对较为剧烈.

2.3 工况参数对整车行驶动力学的影响

2.3.1 车速的影响

设置路面的凸台障碍高度为200mm，车辆分别以20km/h、30km/h、40km/h速度匀速通过凸台障碍，计算得到整车和炮管的垂向、侧向加速度，如图10所示.由图10（a）可知，整车以不同速度通过障碍路面时，垂向加速度均发生突变，其峰值分别为1.2g、3.5g、5g.同时由图10（c）可知，炮管的垂向加速度峰值在不同速度下分别为5g、5.5g、6g，三种速度下差距不大，且均大于整车质心的垂向加速度.整车和炮管在低速通过障碍路面后垂向加速度均能够快速稳定下来.由图10（b）和11（d）可知，三种速度下整车的侧向加速度最大峰值仅为0.1g，炮管的峰值最大值为0.7g.

图10 不同速度下整车和炮管动力学响应Fig10 Dynamic responseof vehicleand barrel at different speeds

可见，随着速度的增大，整车通过凸台障碍路面时，受到的冲击性会变大，炮管的垂向振动会加剧.但车速低于一定速度通过凸台路面时，车辆的稳定性较好.因此，当通过凸台路面时，应适当降低车速，以减少路面对车辆的冲击，减小炮管的振动，提高车辆的行驶平顺性和安全性.

2.3.2 凸台高度的影响

车辆以30km/h速度，分别通过100mm、200mm、300mm高度的凸台障碍路面，计算得到的整车和炮管垂向、侧向加速度，如图11所示.由图11（a）可知，整车以同一速度通过不同高度的凸台路面时，垂向加速度均发生突变，其峰值分别为1.5g、3.5g、4g.同时由图11（c）可知，炮管的垂向加速度峰值在不同凸台高度下分别为5g、7g、10g，均大于整车质心的垂向加速度.整车和炮管在通过障碍路面后，垂向加速度均能够快速稳定下来.由图11（b）和11（d）可知，100mm、200mm障碍高度下，整车和炮管的侧向加速度不大，而通过300mm障碍高度时，整车侧向加速度峰值突变为0.45g，炮管峰值突变为4g.

综合分析可知，随着凸台障碍高度的增大，整车通过凸台路面时，受到的冲击会变大，炮管的垂向振动会加剧.当凸台高度为300mm，接近极限高度时，车辆的稳定性开始变差.因此，在通过较高凸台障碍时，应低速谨慎驾驶，以防止较大的冲击对整车的安全性、稳定性造成影响.

2.3.3 单侧车轮、双侧车轮驶过障碍的影响

设置车速20km/h，凸台高度200mm，使车辆分别以左侧单侧车轮和左右双侧车轮通过凸台障碍路面，两种情况下的整车和炮管响应，如图12所示.由图12（a）可知，以同一速度通过同一高度的障碍路面时，当双轮同时驶过时整车垂向加速度峰值为3g，而单轮通过时峰值仅为1.5g，减小了50%.而由图12（c）可知，炮管的垂向加速度峰值在单、双轮通过时分别为5g、5.2g，相差不大，但均大于整车质心的垂向加速度.在通过障碍路面后，整车和炮管垂向加速度，均能够快速稳定下来.由图12（b）和图11（d）可知，整车的侧向加速度，在双侧轮通过障碍时峰值仅为0.05g，而单侧轮峰值高达1g.炮管的侧向加速度，当双侧轮通过时峰值为0.5g，单轮峰值高达4g，相差8倍.

图11 不同凸台高度下整车和炮管动力学响应Fig.11 Dynamic response of vehicle and barrel at different obstacle heights

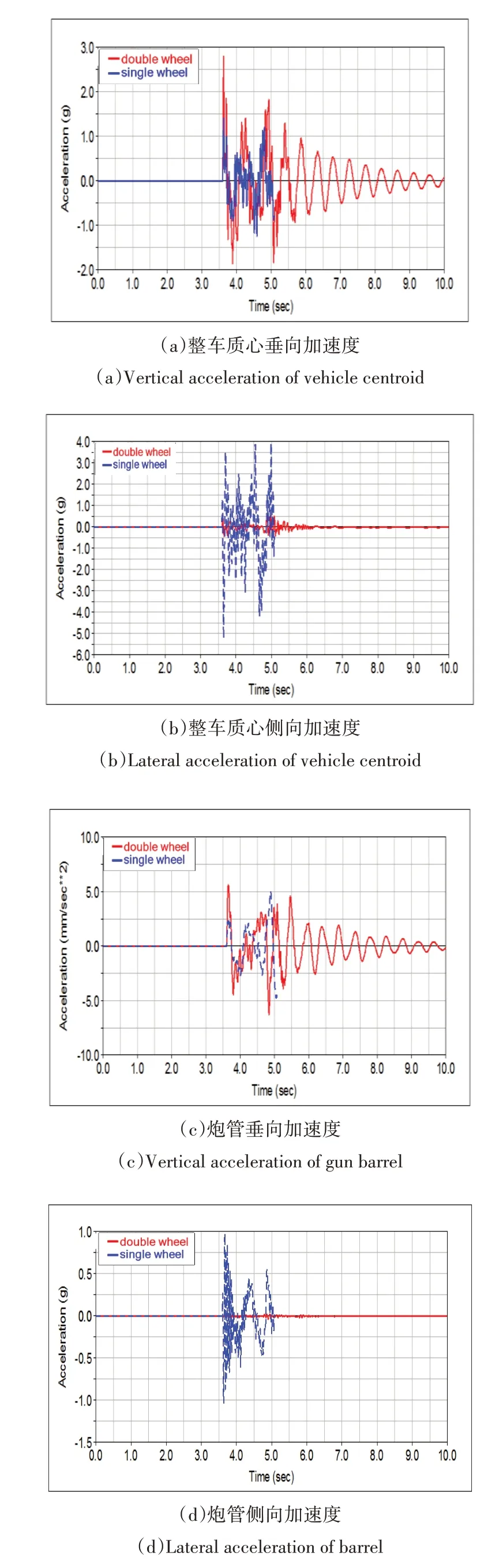
图12 单侧轮、双侧轮通过凸台障碍路面时动力学响应Fig.12 Dynamic response of single wheel and double wheel passing through convex obstacle Road

因此，在车速和凸台高度相同的情况下，单侧轮通过凸台时整车受到的冲击性远大于双侧轮，但对于炮管的垂向振动影响不大，且单侧轮通过时车辆的稳定性会变差.所以，在通过障碍路面时，以单侧轮驶入可以减小路面对整车冲击，以双侧轮驶入可以提高行驶稳定性，减小炮管的水平方向振动.

3 悬架的优化设计

在优化过程中使用的是ADAMSInsight模块，该模块可以进行分组实验设计，通过筛选试验将最灵敏的参数选出，从而得到优化结果.

3.1 优化目标和参数选择

研究障碍路面下整车平顺性的主要目的是使整车在各种工况下的垂向振动处在合理范围.选取整车在20km/h速度通过高度100mm的垂直凸台障碍路面时的垂向加速度为目标函数，并使之最小.选取前中后悬架弹簧的刚度、减振器阻尼这六个悬架物理特性参数作为待优化参数.设定各优化参数在整车允许条件下的变化范围如下；

0.9K≤K≤1.1K

0.9C≤C≤1.1C

3.2 优化结果分析

ADAMSInsight模块可以进行分组实验设计，通过筛选试验将最灵敏的参数选出，从而得到优化结果.本节在Insight软件中生成64种试验组合，运行后返回ADAMS/Car主页面依次仿真.通过优化过程，可显示出各优化参数对目标的影响情况，如图13所示.由图13可知：对垂向加速度的影响大小依次为中悬架刚度、后悬架刚度、前悬架刚度、前悬架阻尼；中悬架对目标值垂向加速度是正影响，后悬架是负影响.

图13 各变量对目标的影响大小Fig13 Impact of each variableon thetarget

根据影响目标值的大小对原悬架刚度和阻尼进行优化，优化前后参数如表3所示.在ADAMS/car中对刚度、阻尼特性文件进行修改，依次替换原刚度、阻尼特性文件，对优化后的车辆动力学模型进行重新仿真计算.仍以20km/h速度通过高度100mm的凸台障碍为例，得到优化后的整车和炮管的垂向加速度，并与优化前进行对比，如图14所示.

表3 优化前后设计变量的对比Table 3 Comparison of design variables before and after optimization

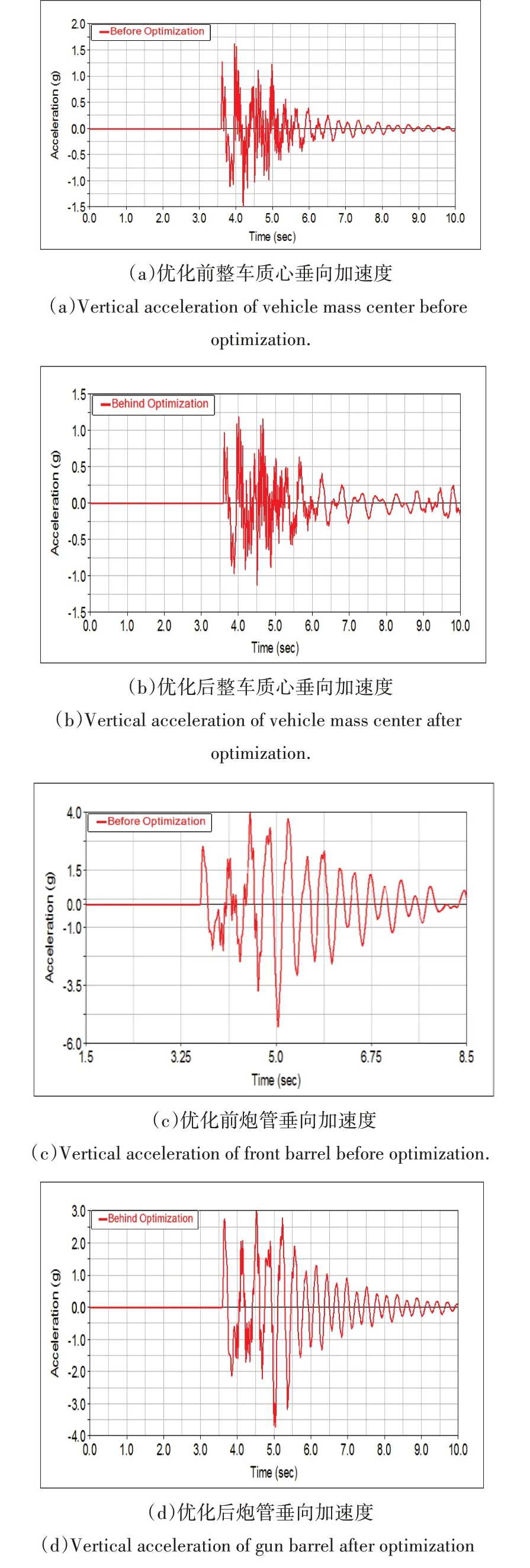
图14 优化前后整车和炮管垂向加速度对比Fig.14 Comparison of vertical acceleration of vehicle and barrel beforeand after optimization

由图14可知，优化前整车通过障碍路面时的垂向加速度峰值为1.5g，优化后为1.2g，减小了20%；优化前炮管垂向加速度峰值为4g，优化后为3.5g，减小了12.5%.由此可知，经过悬架优化后，车辆和炮管垂向加速度峰值均明显减小，车辆通过凸台障碍时的平顺性得到有效提高.

4 结论

建立了带有柔性炮管的刚柔耦合特种车辆动力学模型，仿真了整车和炮管在含凸台障碍路面下的动态响应，分析了工况参数对整车和炮管动态性能的影响，并通过ADAMS/Insight和ADAMS/Car的联合仿真，以平顺性为目标对悬架参数进行了优化.研究结果表明：

（1）炮管弹性变形对车辆和炮管响应的影响不容忽视，有必要考虑炮管柔性建立刚柔耦合车辆模型，以提高仿真计算的准确性.

（2）该特种车辆驶过含凸台障碍路面时会受到较大的冲击，但具有较好的稳定性，且在各种工况下炮管的垂向振动都比车体振动更加剧烈.

（3）适当降低车速可以减少障碍对车辆的冲击、从而减小炮管的振动，有利于提高车辆平顺性；凸台高度越大，对车辆的冲击越大，会影响整车的安全性和稳定性；单侧轮通过障碍可以减小路面对整车冲击，双侧轮通过障碍可以提高车辆稳定性，同时减小炮管的振动.

（4）悬架参数优化后，整车垂向加速度峰值减小20%，炮管垂向加速度峰值减小12.5%，可有效改善车辆通过障碍路面时的平顺性.