基于非规范替换法的连续控制系统离散化方法

李穗 李毅 郎加云

【摘 要】 连续控制系统离散化的常用方法包括欧拉（Euler）法、休恩（Heun）法、龙格-库塔（Runger-Kutta）法、双线性（Tustin）法等，都是采用规范替换法，依据某种映射关系将s域转换到z域，计算速度和精度都有限。在对以上方法进行分析比较的基础上，本文提出了一种非规范替换法对连续时间控制系统进行离散化，仿真结果表明与规范替换法相比，该方法的灵活性更强、离散化精度更高。

【关键词】 连续控制系统;替换法;离散化

【中图分类号】 TP391.7 【文献标识码】 A 【文章编号】 2096-4102（2021）02-0095-03

在现代工业生产中，控制系统的作用越来越重要。随着计算机控制技术、数字信号处理技术、系统仿真等技术的快速发展，在控制系统中引进计算机进行离散控制的做法越发普及。依据连续控制器理论设计的离散控制器，可将连续系统转换成离散系统，成为现代离散控制系统设计常用的方法。连续系统的离散化从数学模型的角度看，是将描述系统的微分方程变换为描述离散系统的差分方程，或将系统的传递函数变换为离散传递函数。

1常用的离散化方法

1.1欧拉法（Euler法）

根据控制理论，s域到z域的变换关系为：

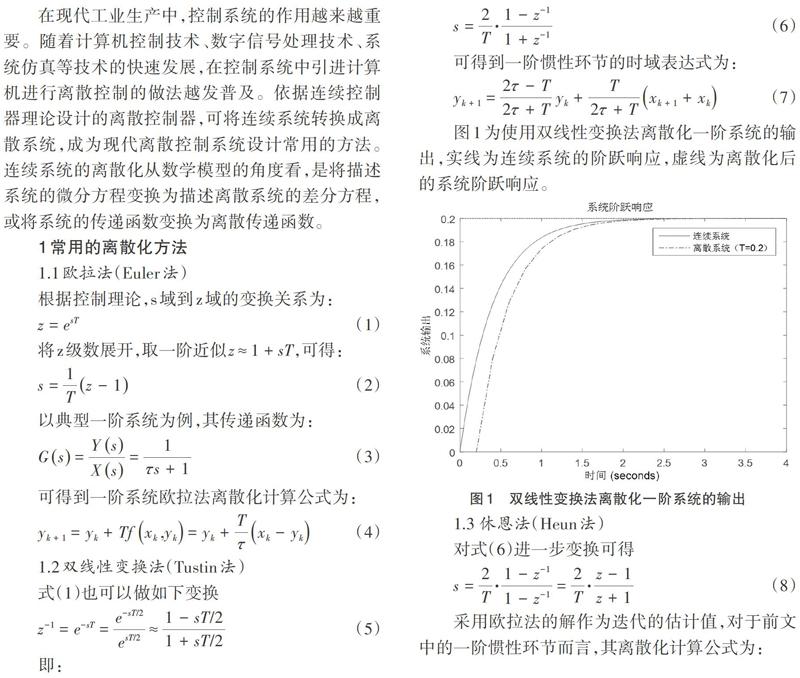
图1为使用双线性变换法离散化一阶系统的输出，实线为连续系统的阶跃响应，虚线为离散化后的系统阶跃响应。

1.3 休恩法（Heun法）

对式（6）进一步变换可得

采用欧拉法的解作为迭代的估计值，对于前文中的一阶惯性环节而言，其离散化计算公式为：

1.4龙格-库塔（Runge-Kutta）法

由式（10）可知，利用泰勒级数得到最终全局误差的阶为N，并且可以通过增大N的值来获得更精确的函数值。但是利用泰勒级数法时，需要首先确定N的值，而且需要计算函数的高阶导数。而龙格-库塔法则是通过计算若干次函数值的方法，构造任意精度的近似公式，典型的龙格-库塔法包括二阶龙格-库塔（RK2）法、三阶龙格-库塔（RK3）法和四阶龙格-库塔（RK4）法。二阶的龙格-库塔法典型算法则为休恩法，三阶龙格-库塔的一种典型算法为如式（12）的Bogacki-Shampine（BS3）法。

图2为使用龙格-库塔变换法离散化一阶系统的输出，实线为连续系统的阶跃响应，虚线为离散化后的系统阶跃响应。

2非规范替换法

上一节中离散化连续系统中表示求导运算的微分算子都是用固定的对应关系替换为表示位移的差分算子（规范替换法），受将n阶微分方程离散化为n阶差分方程的限制，只能用一次多项式或者一次多项式之比的有理分式表示微分算子与差分算子的关系，其离散化精度不超过二阶（欧拉法为一阶精度，双线性变换法为二阶精度）。

为了进一步提高系统的离散化精度，本文采用一种变化的微分算子与位移算子关系进行替换，仿真结果表明，该方法在保证离散化系统阶数不变的情况下，能够获得比规范替换法更高的离散化精度。该方法采用式（13）作为连续系统的微分算子s的近似：

取上式的各阶逼近，以五阶连续系统为例，按式（14）取s各阶逼近来获得相应的离散化系统：

以某五阶连续控制系统为例，其开环传递函数为：

按欧拉法求得对应的离散化系统传递函数为（步距h=0.05）：

按Tustin法求得对应的离散化系统传递函数为（步距h=0.05）：

按照式（14）得到非规范替换法的离散化系统传递函数为（步距h=0.05）：

利用MATLAB对式（16）、式（17）和式（18）所表示的系統进行仿真计算，结果如图3所示，其中图3（a）上方自上而下分别为利用欧拉法得到的离散系统H1（z）、连续系统G（s），利用非规范替换法得到的离散系统H3（z），利用Tustin法得到的离散系统H2（z）的幅频特性曲线。图3（a）下方分别为利用Tustin法得到的离散系统H2（z），利用非规范替换法得到的离散系统H3（z）、连续系统G（s），利用欧拉法得到的离散系统H1（z）的相频特性曲线。图3（b）为系统响应特性曲线放大的结果。

由图3可见，采用非规范替换法得到的离散系统幅频和相频响应误差比采用欧拉法和Tustin法得到的离散系统响应更小，系统更稳定。进一步改变离散步距或者连续系统开环传递函数，所得结论相同。

3结论

通过对欧拉法、双线性变换法、休恩法、龙格-库塔法以及非规范替换法对连续系统离散化的算法分析以及仿真表明，规范替换法离散化过程简单、系统稳定性好，非规范替换法则具有离散化过程灵活、离散化精度较高的特点，在实际应用中需要根据具体情况进行选择。

【参考文献】

[1]赵霞，王祝萍，贾海航.连续系统离散化方法的比较与解析初探[J].工业和信息化教育，2015（10）：71-76，82.

[2]赵广辉，高鑫，方金福，等.连续控制系统固定步长离散化方法性能对比分析[J].鞍山师范学院学报，2018，20（2）：33-39.

[3]张民，黄凯，王田荣.连续控制系统非规范替换法离散化[J].海军工程大学学报，2003（3）：9-13.

[4]吴汉松，陈少昌，徐袭，等.基于非标准替换法的控制系统仿真[J].计算机仿真，2004（7）：72-74.