Index Design and Comprehensive Evaluation of Germplasm Resources of Fruits Based on Mathematical Model of AHP and FCE: Sterculia nobilis Smith as a Case

Li Wen-yan, Wei You, and Zhou Jing

Guangxi Academy of Agricultural Sciences, South Asian Tropical Agricultural Science Research Institute of Guangxi, Longzhou 532415, Guangxi, China

Abstract: The mathematical model of analytic hierarchy process (AHP)—fuzzy comprehensive evaluation (FCE) was applied to comprehensively evaluate the germplasm resources of Sterculia nobilis Smith, and the scientific nature and reliability of the mathematical model was verified by calculating index weights and comprehensive evaluation scores. In this paper, 11 indicators were selected to construct a comprehensive evaluation system from four dimensions of yields, resistances, contents of main inclusions in seeds and tree shapes. AHP method was applied to calculate the index weight of each dimension, after passing the consistency test,FCE method was applied to comprehensively evaluate germplasm resources of S. nobilis Smith. The index weights of the yields,resistances, contents of major inclusions in seeds and tree shapes were 0.5518, 0.2554, 0.1279 and 0.0649, respectively. The yield had the greatest influence on the comprehensive evaluation of germplasm resources of S. nobilis Smith, which was in line with the actual production demand of S. nobilis Smith as a food crop. However, resistances and contents of major inclusions in seeds had limited influence on it, while tree shapes had the least influence on it. After fuzzy comprehensive evaluation, the final evaluation score was 88.00, the corresponding evaluation score was between 4 and 5, and the evaluation results ranged from slight good to good, which indicated that the evaluation weights corresponding to the four dimensions were more scientific and reasonable. In this study, the mathematical model of AHP-FCE was used to establish and evaluate the comprehensive evaluation system of the germplasm resources of S. nobilis Smith. According to the values of index weights and the evaluation results, it showed that the mathematical model was scientific and reliable, and it could provide a new reference method for the comprehensive evaluation of germplasm resources of other fruits.

Key words: Sterculia nobilis Smith, comprehensive evaluation, AHP-FCE mathematical model, germplasm resource

Introduction

Sterculia nobilisSmith, belonging to the genus Sterculia Linn., familySterculiaceae, is an evergreen fruit tree, which originates in south China and has been cultivated in China for more than 1 000 years.S. nobilisSmith is also known as phoenix-eye fruit,nine-layer-skin fruit, etc., its seed has a significant antioxidant effect, and the taste is similar to the chestnut. At the same time,S. nobilisSmith is also the cash forest. In short,S. nobilisSmith is a potential fruit tree resource (Zhaoet al., 2012; Liet al., 2012; Fenget al., 2007). Therefore, it is of great significance to collect and comprehensively evaluate the germplasm resources ofS. nobilisSmith to promote the research on breeding and innovative utilization in China. At present, there is few researches on exploitation ofS. nobilisSmith in China. Zhaoet al. (2012) obtained a higher germination rate ofS. nobilisSmith by sowing the mature seeds after sterilization treatment;Renet al. (2013) found that the seed ofS. nobilisSmith is rich in a variety of nutrients and has significant antioxidant effect; Yanget al. (2016) found that the survival rate of grafting seedlings is the highest and the budding time is the shortest after grafting with terminal buds ofS. nobilisSmith; Wuet al. (2016) concluded that under drought stress,the drought-resistant capacity ofS. nobilisSmith seedlings is slightly higher thanSterculia lanceolataCav. seedlings; Zhouet al.(2016) found that it is more suitable for the growth ofS. nobilisSmith under the condition of about 50% light transmittance; according to the study of Huanget al. (2017),S. lanceolataCav.is more suitable for rootstock, which can solve the problems of lacking of germplasm resources and high cost of seedlings. At present,S. nobilisSmith in China is almost in the wild and semi-wild status, there is no large-scale cultivation, so it is necessary to establish a comprehensive evaluation system to screen out the excellent fruit varieties (lines) suitable for large-scale cultivation.

At present, there are many studies on the selection of evaluation methods, for example, principal component analysis (Christopheet al., 2013), rough set theory (Sirzatet al., 2011), Markov model (Hardlewet al., 2014; Hwanget al., 2013), BP neural network(Liuet al., 2012; Xiaoet al., 2009), etc. These methods can apply certain mathematical theory to solve a certain aspect of evaluation problem and get better results. However, based on the attributes of evaluation objects, there are few studies on selecting more appropriate and reasonable evaluation methods.

Analytic hierarchy process (AHP) is a qualitative,quantitative, systematic and hierarchical analysis method for multiple criteria decision-making from various heterogeneous data (Xueet al., 2019; Chenet al., 2019), and is used widely for analyzing decisionmaking in various real-world applications (Liuet al.,2017). Its advantage is to establish a hierarchical and structured evaluation system for the evaluation and analysis of multi-criterion problems. In contrast to the method of dynamic technique for order preference by similarity to ideal solution (DTOPSIS) (Liet al., 2019), AHP does not require much quantitative data. Fuzzy comprehensive evaluation (FCE)is a comprehensive evaluation method based on fuzzy mathematics. By using the principle of fuzzy linear transformation and the principle of maximum membership, things or objects subjected to multiple factors can be evaluated in an overall and reasonable way. It has the characteristics of clear result and strong system. Based on the characteristics above, the mathematical models of AHP and FCE were applied to construct and evaluate the comprehensive evaluation system for germplasm resources ofS. nobilisSmith in this paper.

Index system of comprehensive evaluation of germplasm resources of Sterculia nobilis Smith

Selection of evaluation indicators

To comprehensively evaluate the germplasm resources ofS. nobilisSmith by AHP, a hierarchical structure model must be established. There were many indicators that affected the comprehensive evaluation.In accordance with the principles of scientificity,actual production demand, hierarchy and horizontal comparability, comprehensive evaluation hierarchy of germplasm resources ofS. nobilisSmith were constructed from four dimensions, namely yields, resistances, main contents of seeds and tree shapes.

This assessment system was comprised of four categories, yield (A1), resistance (A2), content of major inclusions in seed (A3) and tree shape (A4). The yield (A1) was composed of average yield per plant(A11), edible rate (A12) and thickness of pod (A13); the resistance (A2) was composed of insect resistance (A21),disease resistance (A22) and stress resistance (A23);the contents of major inclusions in seeds (A3) were mainly composed of starch content (A31), soluble sugar content (A32) and soluble protein content (A33);the tree shape (A4) was mainly composed of plant height (A41) and crown width (A42). The three-level index system for comprehensive evaluation system of germplasm resources ofS. nobilisSmith was established (Fig. 1).

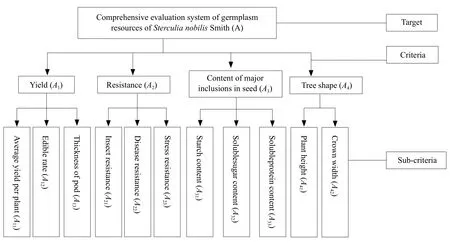
Fig. 1 Hierarchical structure model for comprehensive evaluation system of germplasm resources of S. nobilis Smith

Determination of index weight

Construction of judgment matrix

A judgment matrix was constructed through pairwise comparison to determine weights of criteria and subcriteria, as well as the importance of various indexes factors to the overall goal. Specifically, pairwise comparison of indices in the same level was conducted to determine relative importance. Saaty's method (2011) was used to indicate the relative importance of two factors 'i' and 'j' using a scale of 1-9 (Table 1): "1", equal importance ('i' and 'j' had equal priority in choice making); "3", moderate importance ('i' had slight priority in choice making compared with 'j'); "5", strong importance ('i' had strong priority in choice making compared with'j'); "7", very strong importance ('i' had very strong priority in choice making compared with 'j'); "9",extreme importance ('i' had extreme priority in choice making compared with 'j'); "2", "4", "6" and"8" meant intermediate values (the importance of'i' and 'j' was between the two adjacent degrees);and "reciprocal", if 'j' was compared with 'i', thenaji= 1/aij.

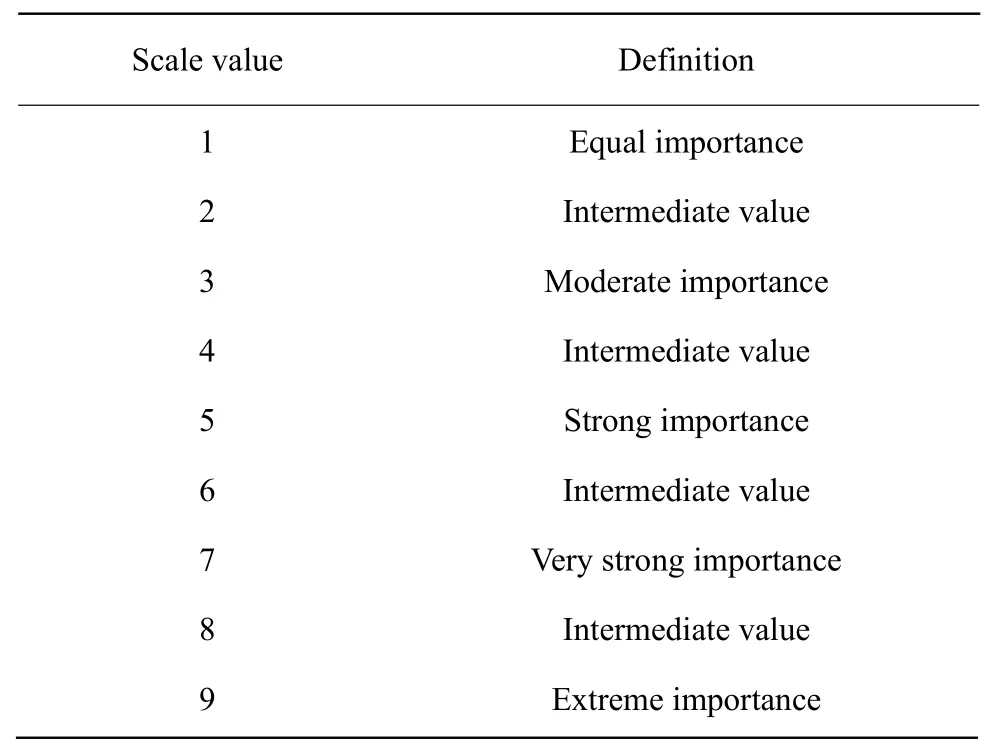
Table 1 Scale values and definition

According to the degree of relative importance,the judgment matrix of indexes in the criterion level and index level could be constructed, respectively.The relative importance of each indicator factor was determined by consulting relevant experts and combining with the actual production demand ofS. nobilisSmith, and then the judgment matrix was obtained, as shown in Tables 2-6.

Table 2 Judgement matrix of criterion level

Table 3 Judgement matrix of A1

Table 4 Judgement matrix of A2

Table 5 Judgement matrix of A3

Table 6 Judgement matrix of A4

Consistency check

The judgment matrix of the criterion level was normalized to the standard matrix, and the maximum eigenvector was obtained by the summation product method. The calculation process was as the followings:

The judgment matrix of the criterion level was normalized to the standard matrix (Table 7).

Each column of the standard matrix of the criterion level was added up to obtain the eigenvectorW',which was 2.2071, 1.0214, 0.5117 and 0.2597, respectively. After normalization of the eigenvectorW', the maximum eigenvectorWwas obtained,and the values were 0.5518, 0.2554, 0.1279 and 0.0649, respectively. Multiplied each column of the judgment matrix by the corresponding maximum eigenvectorW, and the total values were 2.3469,1.0826, 0.5181 and 0.2634, respectively. According to the formula, the maximum lambda Max (λmax)was 4.1503 and the consistency index (C.I.) was 0.0501. Since the number of indicator was 4, the random index (R.I.) was 0.89 (Table 8), and the consistency ratio (C.R.)=C.I./R.I.=0.0563＜0.1, so it was considered that various indicators of judgment matrix in the criterion level passed the consistency test.

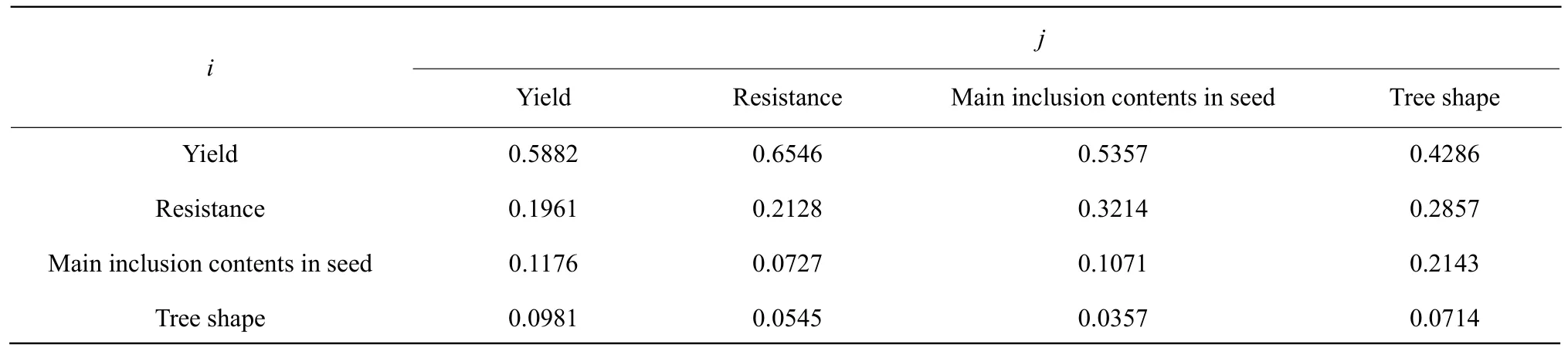
Table 7 Standard matrix of criterion level

The standard matrix was obtained by normalizing the judgment matrix of each index level with the same method, and the maximum eigenvector was calculated by the summation product method, the values fromA11toA13were 0.6480, 0.2299 and 0.1222,respectively; the values fromA21toA23were 0.6651,0.2311 and 0.1038, respectively; the values fromA31toA33were 0.6232, 0.2395 and 0.1373, respectively, and the values fromA41andA42were 0.6667 and 0.3333,respectively. Then, the random consistency ratio of each indicator level was calculated, and the results are shown in Table 8. As it is shown in Table 8, the value ofC.R. of each indicator level was less than 0.1,which indicated that the ranking result of importance of single indicator level was reasonable. Since the tree shapeA4only contained plant heightA41and crown widthA42, there was no consistency problem.

Table 8 Consistency test results

The overall ranking and consistency test of the comprehensive evaluation index system of germplasm resources ofS. nobilisSmith: the total ranking of evaluation levels of germplasm resources ofS. nobilisSmith was obtained after calculating (Table 9).

Consistency test:C.I.=0.5518×0.0022+0.2554×0.0434+0.1279×0.0092+0.0649×0=0.0135,R.I.=0.5518×0.5200+0.2554×0.5200+0.1279×0.5200+0.0649×0=0.4863,C.R.=C.I./R.I.=0.0135/0.4863=0.0278＜0.1.It indicated that the overall ordering of the whole hierarchy was of satisfactory consistency.

Fuzzy comprehensive evaluation of S. nobilis Smith

Determination of evaluation set

According to different satisfaction levels of the evaluators on each indicator factor, the possible evaluation level was determined, which was denoted as the evaluation setV,V=(V1,V2,V3,V4, …,Vn), the evaluation set in this paper was:V=(V1,V2,V3,V4,V5andV6)=(excellent, good, slight good, moderate,qualified and unqualified), the corresponding evaluation scores wereV=(6, 5, 4, 3, 2 and 1), the corresponding assignment scores wereV=(100, 90, 80, 70, 60 and 50).

Determination of evaluation score

According to the evaluation index system, 10 peer experts were invited to score and the scores constituted the evaluation set:P=(P1,P2,P3,P4,P5,P6,P7,P8,P9andP10) (Table 10).

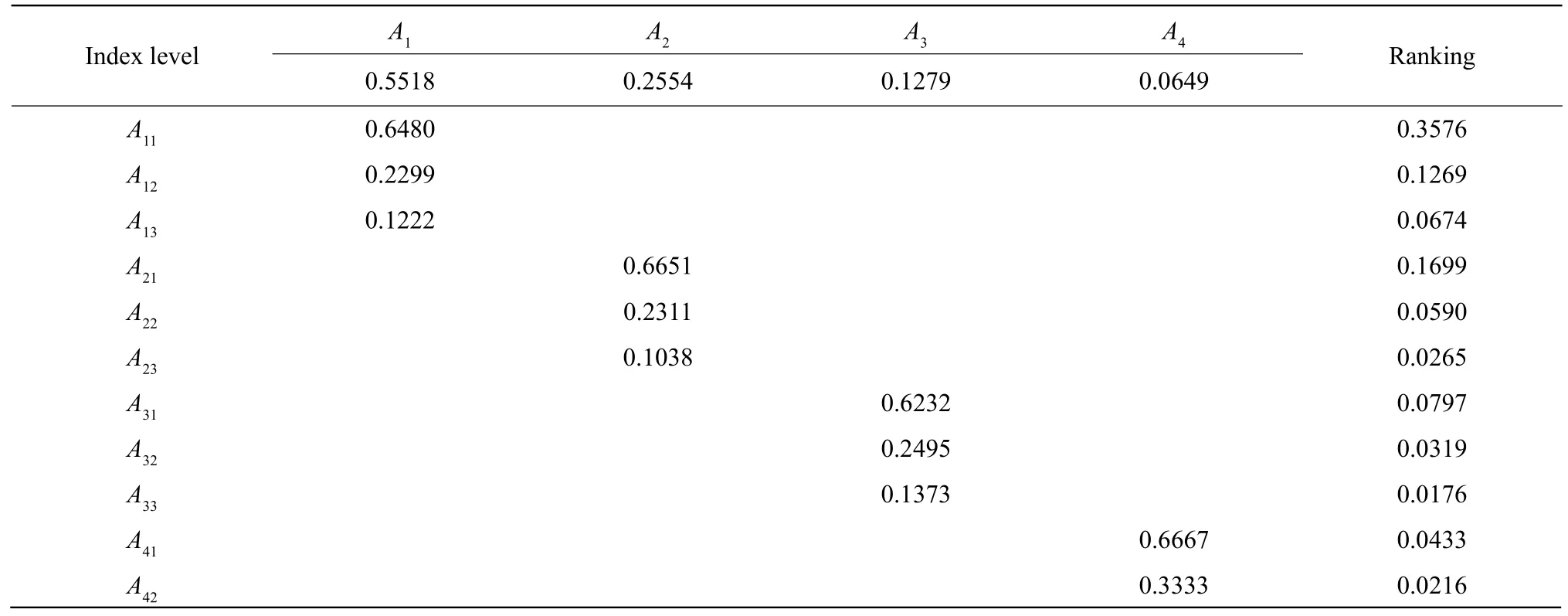
Table 9 Weight of each index and ranking

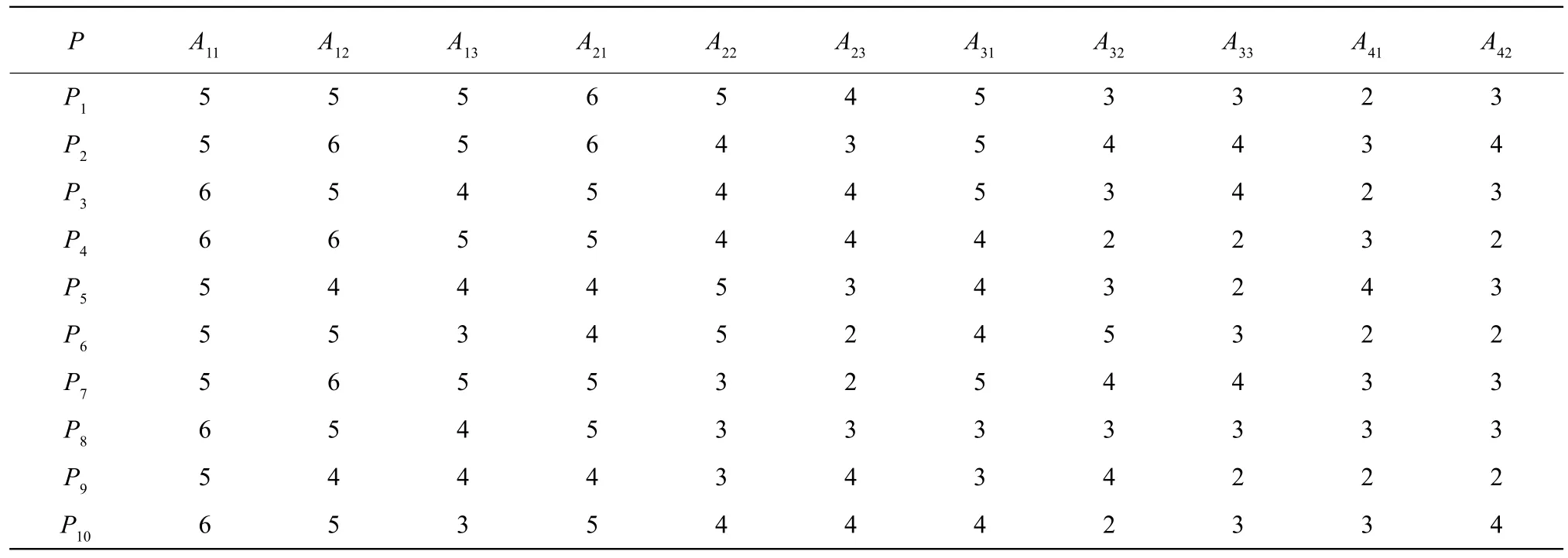
Table 10 Scores by experts

The evaluation sets ofA1,A2,A3andA4were constructed respectively by calculating the frequency,according to the expert scoring results, then filled in the determined weight of each level factor index, and the values are shown in Table 11.

Assuming thatB1,B2,B3andB4were the fuzzy matrices of each second-level factor, respectively,W1,W2,W3andW4were the weights of factor indicator of each second-level, the fuzzy evaluation of the matrices of the four second-level factors wasZi(I=1, 2, 3 and 4) and the fuzzy matrixBof the first-level factor was obtained byZi=WiBi:

The index weight of criterion level wasWi=(0.5518,0.2554, 0.1279 and 0.0649), so the fuzzy evaluation indexZof the matrix of the first level wasZ=WB=(0.0000, 0.0405, 0.1069, 0.1825, 0.4553 and 0.2251),and the evaluation score was calculated as 88.00 by the weighted average method.

Table 11 Index weight and evaluation set

Analysis of comprehensive evaluation system

The final score of comprehensive evaluation system of germplasm resources ofS. nobilisSmith was 88.00 by using AHP-FCE method, the corresponding evaluation score was between 4 and 5, and the evaluation result ranged from slight good to good. It indicated that the weights of the four evaluation factors of the criterion level were more scientific and reasonable, which were 0.5518,0.2554, 0.1279 and 0.0649, respectively. The yield factor had the greatest influence on the comprehensive evaluation of germplasm resources ofS. nobilisSmith. The weights corresponding to yield per plant, edible rate and follicle pod skin thickness of the three indicators belonging to the yield criterion were 0.6480, 0.2299 and 0.1222, respectively and it indicated that the index of yield per plant had the greatest influence on the yield criterion level, which conformed to the actual production demand ofS. nobilisSmith as a woody food crop.The criterions of resistance and main inclusion contents in seeds had the secondary impacts on the comprehensive evaluation of germplasm resources ofS. nobilisSmith. The weights corresponding to the three indexes of insect resistance, stress resistance and disease resistance were 0.6651, 0.2311 and 0.1038,respectively, and the corresponding weights of starch content, soluble sugar content and soluble protein content belonging to the main content of inclusions in seeds were 0.6232, 0.2395 and 0.1373, respectively.The results indicated that insect resistance had the great effect on the resistance criterion and the starch content in seeds had the great effect on the criterion of main inclusion contents in seeds. The tree shape had the least influence on the comprehensive evaluation of germplasm resources ofS. nobilisSmith.

Discussion

The comprehensive evaluation of germplasm resources of fruit trees with AHP-FCE mathematical models had not been reported yet, AHP method was only applied to the comprehensive evaluation of Tuanzao (Liet al.,2019), sugarcane breeding (Wuet al., 2013), and FCE method was not used to evaluate the whole evaluation system.

However, AHP-FCE mathematical model was applied to the assessment of ecological environment (Fan and Liu, 2019; Khoshandet al., 2019; Zenget al.,2016; Xuet al., 2012; Chenet al., 2006), large investment and construction projects (Serrano-Gomez and Munoz-Hernandez, 2019; Jayawickramaet al., 2017),construction safety (Ribaset al., 2019; Leiet al.,2014) and personnel capacity (Albertoet al., 2019;Luan, 2011), etc. The results were satisfactory and scientific.

In this paper, AHP method was used to construct a comprehensive evaluation system on germplasm resources ofS. nobilisSmith including 11 indicator variables and the weight of each indicator factor was calculated. An evaluation set was formed by experts evaluating and scoring different satisfaction levels of each indicator factor. After the fuzzy comprehensive evaluation, the fuzziness that might appear in the evaluation of germplasm resources ofS. nobilisSmith could be effectively converted into digital analysis.In addition, it avoided the disadvantage that the consistency index of judgment matrix in AHP was not easily to meet. However, this method needed a lot of calculation, especially matrix calculation, so how to realize simple and fast calculation should be further studied in the future.

AHP-FCE mathematical model was an evaluation method combining subjective fuzzy evaluation with objective concrete facts, and it was also an evaluation method of combination of qualitative and quantitative analyses.

A certain degree of flexibility was required in establishing the mathematical model of comprehensive evaluation. For general problems, the evaluation data were determined through investigation and discussion. For important issues, expert authority was needed to determine the data. In general, AHPFCE mathematical model provided a systematic,standard and comprehensive thinking method for comprehensive evaluation of germplasm resources of fruit tree. Comprehensive evaluation of germplasm resources of fruit tree was a multi-factor fuzzy evaluation process. AHP-FCE comprehensive evaluation method overcame the uncertainty of indicators and the boundary ambiguity among different levels, improved the accuracy and reliability of evaluation results and was a kind of evaluation method with extensive practical value.

Conclusions

The safety comprehensive evaluation system on germplasm resources ofS. nobilisSmith was established on the basis of four aspects, yield, resistance,contents of major inclusions in seeds and tree shapes by applying AHP-FCE mathematical model. The system was consisted of 11 indicators, including average yield per plant, edible rate, thickness of pod,insect resistance, disease resistance stress resistance,starch content, soluble sugar content, soluble protein content, plant height and crown width. The final comprehensive evaluation score of germplasm resources ofS. nobilisSmith was 88.00, the corresponding evaluation score was between 4 and 5 and the evaluation results ranged from slight good to good.

The innovativeness of this study was that it used AHP-FCE mathematical models to comprehensively evaluate germplasm resources ofS. nobilisSmith.Furthermore, it could provide a theoretical basis and technical support for establishing comprehensive evaluation system on germplasm resources of other fruit trees.