基于飞机性能的连续爬升程序建模和油耗分析
徐冬蕾 丁冬进, 2 肖刚* 王国庆
(1. 上海交通大学,上海 200240; 2. 中国东方航空集团有限公司,上海 201100)
0 引言
面对2020年年初以来运输量的锐减和收益的大幅下降,航司亟需采取多个措施来降低运营成本,提高运行效率。研究表明燃油成本占据直接运营成本(DOC)的23%[1],同时碳排放也成为部分地区的评价和交易影响因素,航司需要为超出免费配给限额的碳排放支付购买成本[2-3]。这就要求飞机需要以更高效的方式飞行,减少因为管制限制造成的燃油消耗。国际民航组织ICAO在文件Doc 9750《全球空中航行计划》中提出了“航空系统组件升级”(ASBU)计划,针对四个绩效改进领域对新一代空中交通管理(ATM)系统的实现提出了目标和计划[4]。在ASBU计划路径下,要达到高效的飞行路径的目标效益,需要拥有连续下降运行(CDO)、基于航迹运行(TBO)、连续爬升运行(CCO)、遥控驾驶航空器系统(RPAS)的能力。由于爬升阶段的大推力设置导致了大量的燃油消耗,提升爬升阶段运行效率能够在排放和噪声上有着巨大的环境效益和经济效益,为优化吞吐量、提高灵活性、确保燃油效率的高效爬升剖面以及提高拥塞终端区的容量提供了机会,其成功实施也可以为新一代ATM理念的达成积累经验。
而相比国外较成熟的运行经验[5-10],国内因为空域限制的问题,基于性能的导航(PBN)技术不能够完整的实施,对于改善航行效率的终端区飞机进离场的连续运行程序,也受到了空域管理的制约,目前正处于一个理论探索和试验相结合的阶段,大规模的推广暂未展开[11]。国家正在积极改革和完善空域管理体系,提升空域使用效率,逐步缩小在空域灵活性上与欧美国家的差异,因此本研究针对CCO的设计方法进行总结归纳,提出了基于飞机性能的建模方法和燃油经济性分析方式,并结合实际航线进行模拟计算和效益分析,为我国未来CCO的设计实施提供了可行的参考。
1 连续爬升程序研究现状
传统的爬升飞行程序遵循ICAO制定的标准仪表离场(Standard instrument departure,简称SID),以阶梯爬升的形式进行高度和速度控制,ATC对飞机进行指挥干预确保离场的安全进行。仪表离场程序定义了程序设计梯度(PDG)、速度范围、超障余度和高度、转弯高度和速度参数,在未收到航迹更新的飞行许可之前,需要保持在一定高度进行平飞,不能有高度的变化。连续爬升运行模式可以有效优化SID离场程序,如图1所示,让飞机在实时接收管制指令的同时不间断地进行爬升,减少平飞段,实现快速离场。

图1 CCO与阶梯式爬升对比示意图
ICAO在2013年发布了文件Doc 9993《连续爬升运行(CCO)手册》,提供了设计思路和实施指导。文件中定义CCO为“一种通过空域设计、程序设计和空中交通管制而实现的运行”,“运行期间,离场航空器通过利用最佳爬升发动机推力,在最大程度上不受干扰地以爬升速度爬升,直至到达巡航飞行高度层”[12]。当前研究对于CCO的设计和评估主要分为两种方式:
1)直接评估法——利用数据开展评估。为了分析CCO对实际运行的影响,相关机构对统计的运行数据进行分析,通常包括每次飞行爬升总时间、平飞时间占比、燃油消耗量、碳排放量等。
2)间接评估法——利用模型拟合估计。通过对飞机运行性能进行建模,进而构建航迹预测、交通流预测和容量预测等空管模型。欧控局(Eurocontrol)提出了一套飞机性能模型及相关数据库(Base of Aircraft Data,简称BADA模型),因其数据开源、机型完善的特性,被广泛用于ATM研究中。BADA数据以ASCII码形式储存,共包含了400余种航空器机型有关操作性能参数及航空公司程序参数等数据,提供了气动和推力系数,可用于航迹仿真和预测[13]。Rosenow[14],Dalmau[15]等通过BADA模型相关系数计算出CCO对燃油消耗的节省量,指出CCO在繁忙交通流中提升终端区容量的效益。南京航空航天大学的黄倩文、张明等人利用QAR数据对BADA燃油消耗模型进行气动数据修正,提高了模型的精确度[16-17]。
本研究使用基于飞机性能模型的方法来对CCO进行设计和研究。相比于需要实际运行数据的直接评估法,间接评估法更加适合在前期论证阶段中使用仿真进行最优方案探究和效益分析。
2 飞机性能模型
飞机性能模型是构建飞机爬升航迹和计算油耗的关键。性能模型分为全能量模型和动力学模型,参考欧控局实验中心BADA用户手册[18],相关机型数据在BADA 3.15中获取。
BADA飞机运行性能模型包括机型名称、飞机重量、飞行包线、气动、推力、油耗和地面活动这7个模块,数据以ASCII文本的形式显示在OPF文件中,分别包括以下主要参数信息:
1)机型模块:包括机型的ICAO代码、发动机数量、型号及类型(包括喷气式、涡桨式和活塞式)、尾流类型(分为Heavy、Medium和Light);
2)重量模块:包括参考重量、最大和最小重量等参数,单位为t;
3)飞行包线模块:包括高度和速度等包线参数;
4)气动模块:包括机翼面积、五种飞行阶段(CR、IC、TO、AP、LD)的升阻系数等参数;
5)发动机推力模块:包括用于计算最大爬升推力和巡航、下降推力的各种系数;
6)油耗模块:包括各类油耗系数;
7)地面运动模块:包括最大重量下起降场长、翼展和机身长度等参数。
2.1 全能量模型
全能量模型(Total Energy Model,简称TEM)遵循能量守恒原理,把航空器看作质点,认为作用于航空器的外力所做的功转化为动能和势能,航空器爬升阶段的能量模型为:
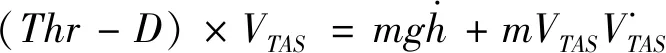
(1)
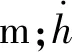
本研究选取上海浦东机场(PVG)飞巴黎戴高乐机场(CDG)航线为实验对象,机型为波音777-300ER,其数据如表1所示。

表1 波音77W机型和性能数据
2.2 动力学模型
飞机在爬升过程中受到自身重力、发动机推力、升力、阻力共同作用,其受力状态如图2所示。

图2 爬升过程受力图
假设飞机在运动方向上的速度为VTAS,飞机受力公式为:

(2)
式中:α为攻角,飞机中轴与运动方向的夹角,°;γ为航迹角,飞行轨迹与水平线的夹角,°;θ为俯仰角,中轴与水平线的夹角,°。
由于民用飞机的运行时不允许有大角度的俯仰机动飞行,因此速度法向的加速度可以忽略不计,因此:
L=mg×cosγ
(3)
式中:L为升力,由气流与机翼作用压差产生,N。
通常情况下,航迹角γ和攻α角都很小,因此可以采用近似处理(γ用弧度制表示):
sinγ≈tanγ, cosγ, cosα≈1
(4)
因此,公式(2)和(3)又可以表示为:

(5)
L=mg
(6)
从公式(5)和(6)可以得出航迹角的表达式:

(7)
式中:L/D为升阻比。
引入升阻比L/D来计算航迹角γ。升阻比体现了飞机的气动效率,升阻比越大,意味着升力更大或阻力更小,飞机拥有更好的爬升越障能力和更大的爬升梯度。离场程序中通常会根据当地地形、障碍物情况等对飞机的爬升梯度作出要求,一般对于爬升梯度的定义是单位水平距离升高的高度。
升力、阻力都是飞机的气动力,与气动构型有关,表达式为:

(8)

(9)
式中:CL为升力系数;CD为阻力系数;ρ为空气密度,kg/m3;S为机翼总面积,m2。
阻力又可以划分为零升阻力(包括摩擦阻力、构型阻力等)和诱导阻力(由升力产生的阻力,例如涡致阻力等)[19],在标称条件下(即BADA 3模型中定义的除了进近和降落阶段的其他运行阶段),阻力系数CD为升力系数CL的函数,表达式为:

(10)
式中:CD0为寄生阻力系数;CD2为诱导阻力系数。
升力系数CL可以通过表达式(6)和(8)推导得出:

(11)
3 航迹生成
本研究使用最大爬升推力进行爬升,计算公式为:
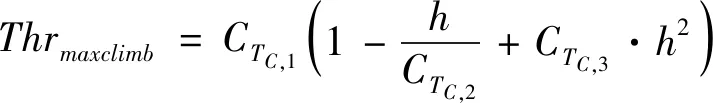
(12)
式中:CTC,1,CTC,2,CTC,3为推力相关系数。
根据表达式(1)得到的垂直剖面的微分方程为:

(13)
式中:ESF为能量分配系数。

(14)
质量的变化通过燃料消耗模型来计算,燃油消耗的公式在第4节中具体给出:

(15)
引入单位时间Δt,将航迹曲线分为由n个微小时间段组合构成的飞行轨迹,选取第i和i+1航迹点(i=1…n),ti到ti+1时间段时间间隔Δt,垂直剖面上高度变化为Δh,水平剖面上距离变化为Δx,航迹角为γ,如图3所示。

图3 微元时间段航迹曲线示意图
h(ti+1)=h(ti)=dh
(16)
VTAS(ti+1)=VTAS(ti)+dVTAS
(17)
根据公式(14)可以得出速度变化量:

(18)
ESF确定了在选定的速度剖面下爬升和加速的能量配比,模拟了飞行员在操控飞机,通常情况下取0.3。
为了对比阶梯爬升和CCO爬升的运行效率和燃油消耗差异,在本研究的仿真环境下建立阶梯爬升的模型。飞机的起始重量为237 600 kg。以飞机从爬升阶段起点为开始,记开始时间为t1=0 s,高度设置在1 500 ft,飞机襟翼和起落架均收起,以洁净构型爬升,速度为CAS 250 kts;在高度到达FL100(10 000 ft)以后,飞机改平飞加速至CAS 310 kts,并继续以该速度进行第二阶段的爬升至顶点HTOC(30 100 ft)。阶梯爬升的阶段描述如表2所示。

表2 阶梯爬升过程描述
CCO模式下的运行过程如表3所示,以飞机从爬升阶段起点为开始,记开始时间为t1=0 s,高度设置在1 500 ft,飞机襟翼和起落架均收起,以巡航构型爬升,速度从CAS 250 kts逐步加速到爬升速度310 kts,保持匀速上升直到爬升顶点(30 100 ft)。

表3 CCO爬升过程描述
计算得到阶梯爬升和CCO垂直剖面的航迹图,表示为高度-时间曲线,如图5所示。阶梯爬升和CCO均使用最大爬升推力进行爬升,以实现快速离场。到达最高点时,阶梯爬升用时928 s,CCO用时878 s,可以看出在离场时间效率上CCO有着一些优势。
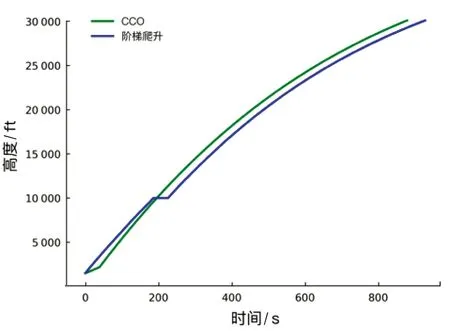
图5 阶梯爬升和CCO垂直剖面图
4 油耗分析
油耗大小取决于发动机推力的大小,对于喷气式飞机来说,其推力燃油消耗率比为:

(19)
式中:η为推力燃油消耗率比,kg/(min·kN);Cf1为第一单位推力燃油消耗系数,kg/(min·kN);Cf2为第二单位推力燃油消耗系数,knots。
结合爬升阶段的推力便可推出单位时间燃油消耗量为:

(20)
式中:fclimb为单位时间燃油消耗量,kg/min。
开始时间t1到爬升结束时间tn内总爬升阶段油耗为:
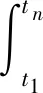
(21)
式中:WF为燃油消耗重量,kg。
仿真结果中阶梯爬升总计耗油3 935 kg,CCO总耗油为3 796 kg,通过使用CCO可以减少爬升过程中的油耗。
5 冲突调解
传统的阶梯爬升使用来自ATC的高度限制和速度限制来调控先后离场飞机之间的距离,在垂直剖面上分配了高度层,来避免不安全的事件的发生。由于其特性,管制员不能对正在实施CCO程序的飞机给出平飞指令,因此当发生冲突的时候,飞机需要调整飞行航迹和速度以实现冲突的解脱。以依次离场的波音777-300ER飞机和A320飞机为例,起飞重量分别为237 600 kg和64 000 kg,离场间隔时间为120 s。
本文提出了一种通过CCO动态速度调节冲突解脱的算法,针对两架实施CCO离场的飞机,首先进行冲突时间的预计,当发生垂直高度差不满足规章要求的最小间隔时,对飞机实行速度控制,实现动态垂直间隔调控和冲突解脱。
冲突时间点预计算法:分别计算前后两架飞机的CCO爬升航迹,并进行高度差计算和判断,求出冲突时间,算法如表4所示。

表4 冲突时间点预计算法
实际仿真的航迹如图6所示,预测的冲突时间为525 s,并持续到A320爬升结束,因此需要调整A320的爬升航迹。

图6 波音77W与A320前后离场冲突
速度调控算法:当冲突发生时,调整后机的CCO CAS速度,从冲突时间点开始重新预测新的航迹,并再次进行冲突判断,算法如表5所示。

表5 速度调控算法
经过速度调节后,新的航迹预测如图7所示,A320的速度调整如图8所示。经过再一次的冲突判断,新航迹不存在冲突,因此后机可以安全进行爬升,A320的新航迹的油耗预计从854 kg提升到了874 kg,爬升时间从571 s提升到了587 s,与最佳CCO剖面相比效率有所降低,但相比于阶梯爬升618 s和913 kg的油耗,CCO依然有着优势。

图7 用冲突解脱方法预测的新航迹

图8 后机速度调整曲线
6 结论
本文利用BADA飞机性能模型及数据对CCO程序进行了建模,通过仿真验证得出在同一建模环境下,相比于阶梯爬升,CCO能够缩短爬升时间并节约燃油,并提出了一种冲突解脱的方法,为CCO的安全实施提供参考。下一步研究将细化对大气环境的模拟,加入风的扰动因素,提高模型精确度;并考虑包括进场在内的多种冲突形式,以燃油最优为目标分别给出解脱方法。

