惯导系统转位条件下的误差特性分析
史国荣,周琪,田宇
(1.海军装备部,陕西西安,710065;2.航空工业西安飞行自动控制研究所,陕西西安,710065;3.航空工业西安飞行自动控制研究所,陕西西安,710065)
0 前言
捷联惯性导航系统的性能在很大程度上取决于运载体的运动。捷联惯性传感器要承受运载体在其全程飞行轨迹上产生的航向和姿态变化以及角速率的影响。这与应用于稳定平台导航系统的惯性传感器明显不同,因为稳定平台导航系统的传感器在选定的坐标系中固定,并且不承受运载体的动态旋转运动。上述这些运动被动地来自于载体运动。此外,随着旋转调制惯性导航系统的发展,捷联惯性导航也被主动地旋转,从而实现误差抵消作用,提高导航精度。
本文将针对上述应用场景的载体运动与调制系统技术[1],重点分析捷联惯性导航传感器误差的方位转位所产生的系统影响,从而来阐述捷联惯性导航系统性能与此类运动的相关性。
本文将首先从惯性导航舒拉回路的状态方程入手,推导由于传感器误差的转位变化产生的系统响应解析表达式,以此来分析导航误差的误差特性。之后,再从控制系统频域特性的角度来定性阐述转位变化产生的系统响应特性。
1 舒拉回路分析
简化问题的分析,研究传感器误差转向所产生的影响,可用惯导单通道舒拉回路[2]为研究对象。在此舒拉回路中不考虑地球自转对惯导舒拉回路的影响,从而简化对问题的分析。
根据图1舒拉回路系统框图列写状态方程为:

图1 舒拉回路框图

将(1)式写为状态方程形式:

系统误差X(t)由两类误差源引起:元器件误差,陀螺漂移ε与加计零位∇,并且假设其为常值,它对系统产生的响应为阶跃响应;系统初始误差,初始平台偏角误差φ(0)与初始速度误差δV(0),它对系统产生的响应为脉冲响应。对(2)进行拉式变换,如下:

该方程的解为:

将其写为矩阵形式,可得到:

具体形式如下:

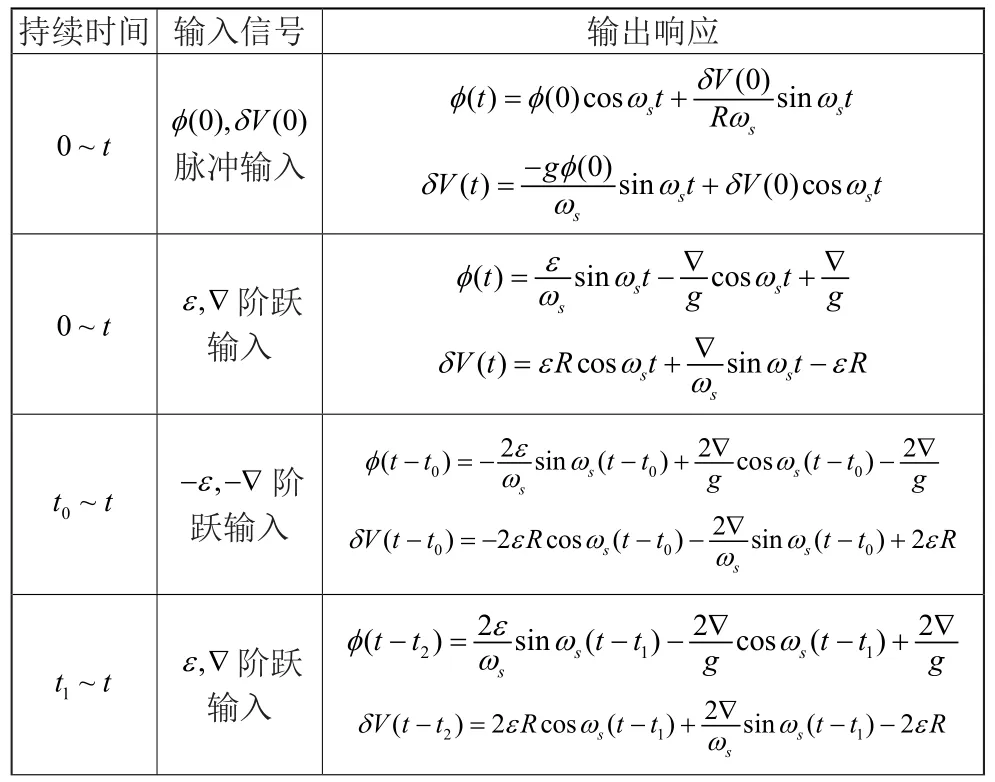
再对式(6)与式(7)进行拉式反变换,得到时域解析表达式:
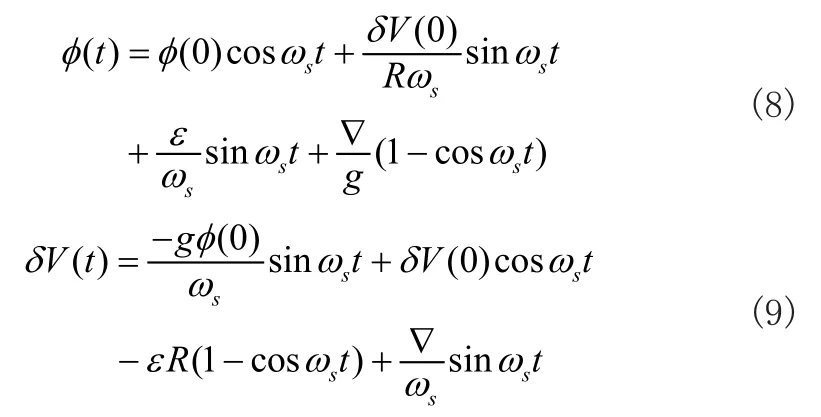
2 陀螺漂移影响分析
陀螺漂移的转位影响可以看作为多个信号的叠加。暂且以一个转向过程为例说明。第一个信号为:在转向前(t≤t0,t0记为第一个转向时刻)陀螺漂移假设为ε,此后(t>t0)为0,可以看作为t0时刻进行了一次补偿;第二个信号为:陀螺漂移为-ε(t0<t≤t1),此后 (t>t1)为0,可以看作为t1时刻进行了一次补偿。每个信号都可以看作为陀螺漂移持续一定时间t0后,进行了一次补偿。示意图如图2所示。本节将按照上述的分解形式,对单个独立的陀螺漂移补偿过程展开分析。

图2 陀螺漂移信号合成示意图
在t0时刻对陀螺漂移进行补偿,即在t>t0时陀螺漂移为0。在单纯分析对陀螺漂移补偿影响时,可暂不考虑加计零位的影响,所以在0<t<t0时φ(t)与δV(t)分别为:

假设在0时刻无初始误差,所以:

而在t>t0时无陀螺漂移误差,此时系统的初始状态误差为φ(t0)与δV(t0),所以φ(t)与δV(t)为:

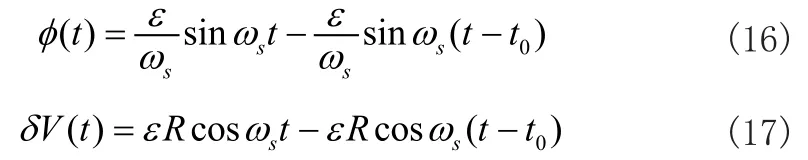
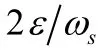
从补偿后的误差传播方程可以看出,当φ(t0)与δV(t0)均为0时,对陀螺漂移补偿可使得系统无误差,即φ(t)与δV(t)为 0。当

在前述的假设条件下,所以可以看出在整数倍的舒拉周期上对陀螺漂移的补偿可以消除整个系统误差。当补偿时刻在半个舒拉周期的奇数倍时刻,即t0=n·42.2min,(n=1,3,…,2 k+1)时,φ(t0)=0,δV (t0)=-2εR,将其带入(14)与(15)后为:

可以看出补偿后的平台偏角误差与速度误差的振荡幅值为补偿前的2倍,所以此时刻对陀螺漂移的补偿会对系统的误差产生副作用。由于补偿了陀螺漂移,可以有效抑制位置误差的发散趋势,但是陀螺漂移的补偿时刻会对补偿效果产生不同的影响,有可能导致振荡幅值增大。
下面来讨论当初始平台偏角误差φ(0)与初始速度误差δV (0)不为零时,在t0时刻进行陀螺漂移补偿所引起的误差响应传播。当有初始误差时,在t0时刻系统的平台偏角误差φ(t0)与速度误差δV(t0)分别为:
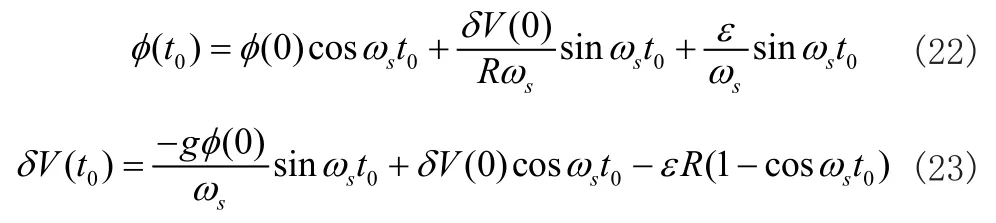
在t0时刻对陀螺漂移进行校正,t>t0时系统误差传播为:

将(22)与(23)分别带入(24)与(25)可得:
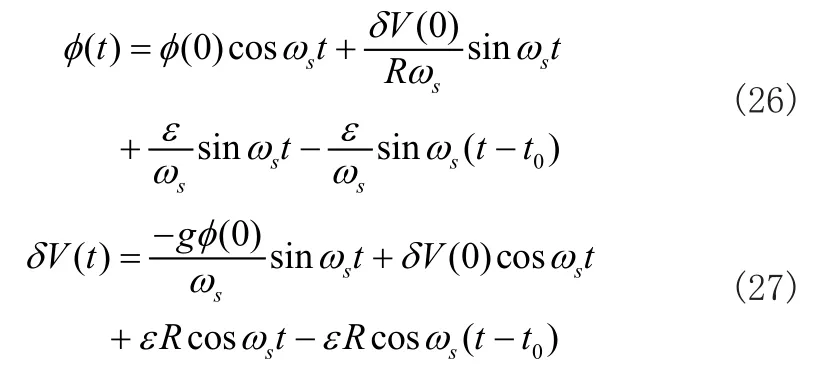
从上式可以看出当存在初始状态误差时,对陀螺漂移的补偿也会具有风险,同样在补偿后,会产生原有陀螺引起的平台偏角的振幅加倍。这种情况的产生完全是由陀螺漂移补偿时刻来决定的,而与初始的系统误差无关。
3 加计零位影响分析
加计零位的影响分析与陀螺漂移的影响分析类似,以单个补偿过程进行推导。
对系统加速度计零位补偿如图3所示,在t0时刻对加速度计零位进行补偿,即在t>t0时加速度计零位为0。在单纯分析对加计零位补偿影响时,可暂不考虑陀螺漂移的影响,所以在0<t<t0时φ(t)与δV(t)分别为:

图3 加计零位补偿示意图

下面来讨论当初始平台偏角误差φ(0)与初始速度误差δV (0)不为零时,在t0时刻进行加计零位补偿所引起的误差响应传播。当有初始误差时,在t0时刻系统的平台偏角误差φ(t0)与速度误差δV(t0)分别为:

在t0时刻对加速度计零位进行校正,t>t0时系统误差传播为:
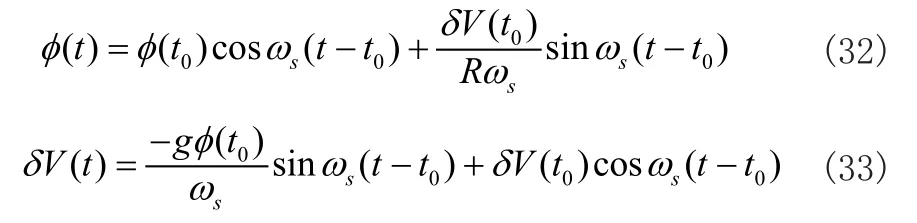
将(30)与(31)分别带入(32)与(33)可得:
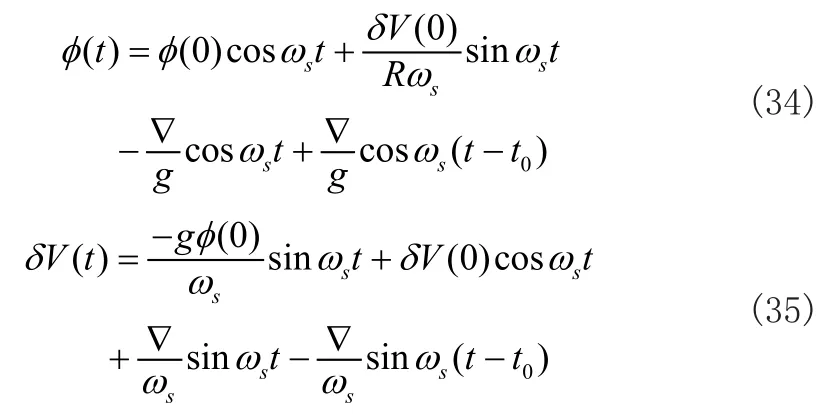
从式(34)和式(35)可以看出当存在初始状态误差时,对加计零位的补偿也会具有风险,同样在补偿后,会产生原有加计零位所引起的平台偏角的振幅加倍。同样,这种情况的产生完全是由加速度计零位补偿时刻来决定的,而与初始的系统误差无关。
4 传感器误差的转位影响分析
由于惯导误差可看作为线性系统,则根据线性系统的叠加性原理[3],可综合考虑陀螺漂移误差与加计零位情况下,在t0时刻补偿后,t>t0时系统误差传播方程为:

从上述两方程可以看到,同样会产生振幅增加的风险。如果当t=t0时刻,将传感器误差反向,即t>t0时,陀螺漂移为-ε,加计零位为-∇,那么系统误差传播为:

带入φ(t0)与δV(t0)得:

若当每半个舒拉周期将传感器误差进行反向,那么系统误差的振幅将不断翻倍,并且趋向发散。
下面研究对于如图4的陀螺漂移与加计零位对系统的影响。
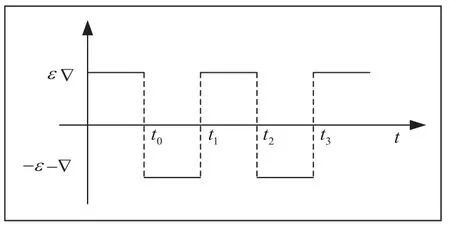
图4 陀螺漂移与加计零位示意图
对于任何信号进行分解,可看作是不同信号的叠加。以上述陀螺漂移激励信号为例,可以认为是如下信号的叠加,并对于线性系统,叠加的输入信号通过线性系统等于输入信号响应的叠加[4]。

从上面的分解项来看,当误差源反向时刻t0,…,tn为半个舒拉周期42.2分钟的整数倍时,会使系统振荡的振幅累积,从而导致系统不稳定呈发散趋势。具体仿真结果如图5所示。
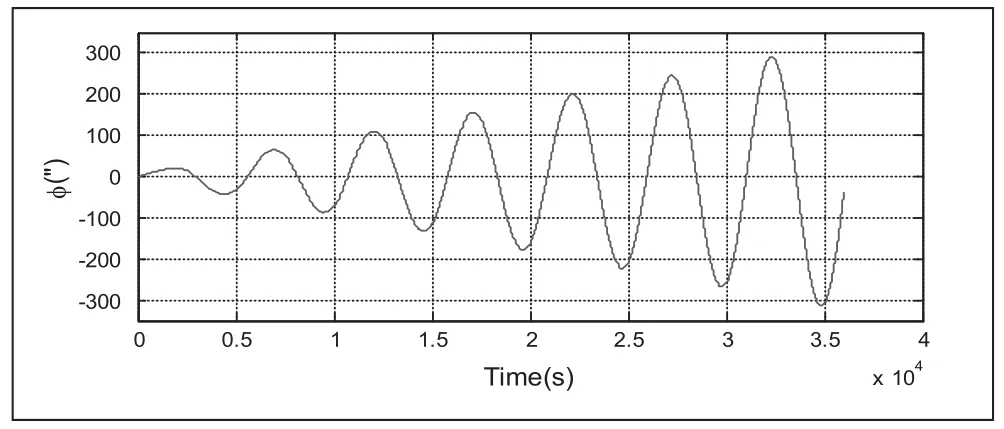
图5 误差影响仿真
这一现象也可以通过舒拉回路的频率响应来分析。通过舒拉回路的状态方程可以得到其传递函数为:
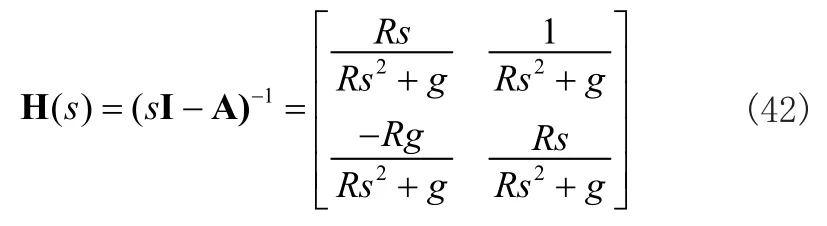
图6~图7给出相应的频率响应曲线。

图6 陀螺漂移与加计零位对平台偏角的频率响应

图7 陀螺漂移与加计零位对速度误差的频率响应
5 结论
从频率响应曲线可以看出,无论是陀螺漂移误差还是加计零位对系统误差的谐振频率都为ωs,并且在谐振频率处具有相当大的峰值增益,使得舒拉回路产生谐振导致发散。这种现象可以通过捷联惯导舒拉蹦(Schuler Pump)实验来验证[5]。在捷联惯导中,当惯导系统以42.2min的间隔进行一系列180°的航向转动,由于导航系固定不动,而载体系进行转动,那么在导航系统看来,其等效的东、北向传感器误差呈交替正负现象,这种情况类似于上述对传感器误差补偿的分析。因此这种舒拉蹦效应会使得捷联惯导的姿态精度发散。从控制系统的角度可以解释为,惯导系统的舒拉回路是临界稳定系统,其谐振频率为舒拉频率,当外界扰动的输入在该频率点上,将产生系统的自激,使得系统发散。
但是随着转位频率的提高和降低,均会使得系统误差在一定程度上减小。例如,通过旋转调整技术可以将传感器的误差进行抵消评价,从而降低了系统误差的累积。此外,地球自转也可以看作为对惯导系统的一个转位调制源,惯导纬度误差在大于24小时的长周期内不发散[6]就是这种因素产生的效果。
由于捷联惯导在方位转位情况下有上述的误差特点,因此需要在具体应用时多加考虑,如周期盘旋的侦查机、反潜机等类似载体,尽量避免捷联惯导纯惯性导航。

