蒙特卡罗模拟中基于双向链表的元胞链表方法
王逸梅, 王少云, 童朝晖
蒙特卡罗模拟中基于双向链表的元胞链表方法
王逸梅, 王少云, 童朝晖*
(宁波大学 物理科学与技术学院, 浙江 宁波 315211)
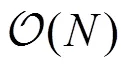
蒙特卡罗方法; 非局域移动; 双向链表; 元胞链表方法
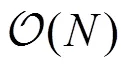
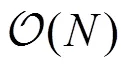
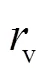
1 方法和算法
这一部分详细描述了基于双向链表的元胞链表方法, 并且给出了相应的Fortran伪代码. 首先, 描述了双向链表的构造和如何调用其中的正向链表来计算能量. 然后, 描述粒子删除和插入后双向链表的更新. 最后, 使用元胞链表的方法来实现Metropolis算法中粒子的随机移动和非局域移动.
1.1 构建元胞链表并计算体系能量
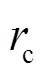
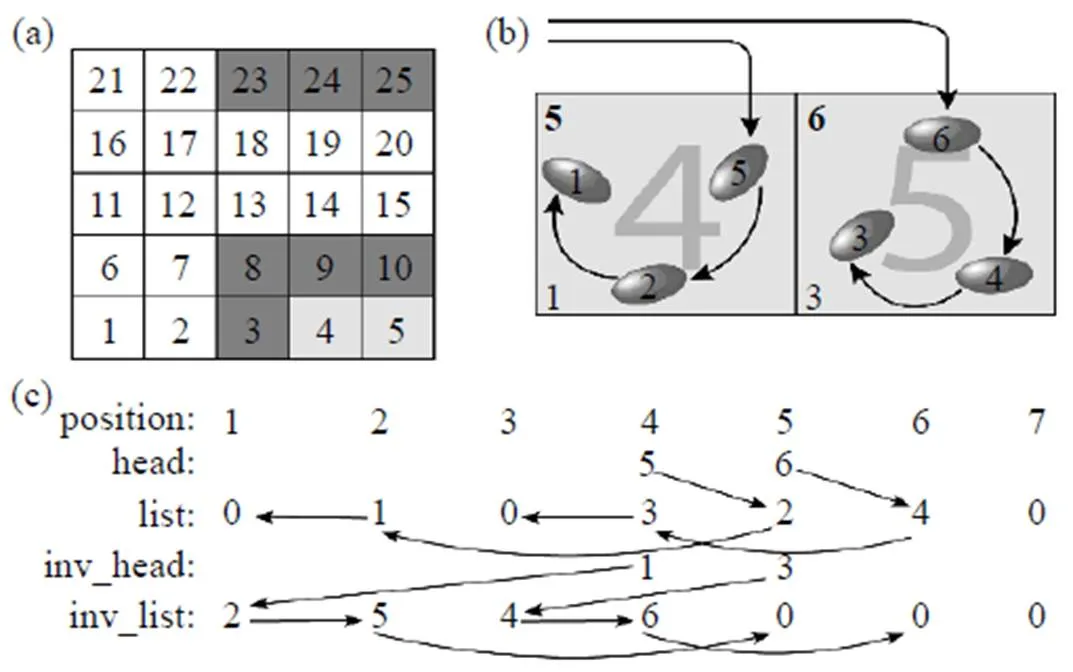
图1 二维元胞链表方法
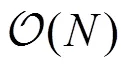
1.2 粒子删除

表1 算法1、2、3的Fortran伪代码
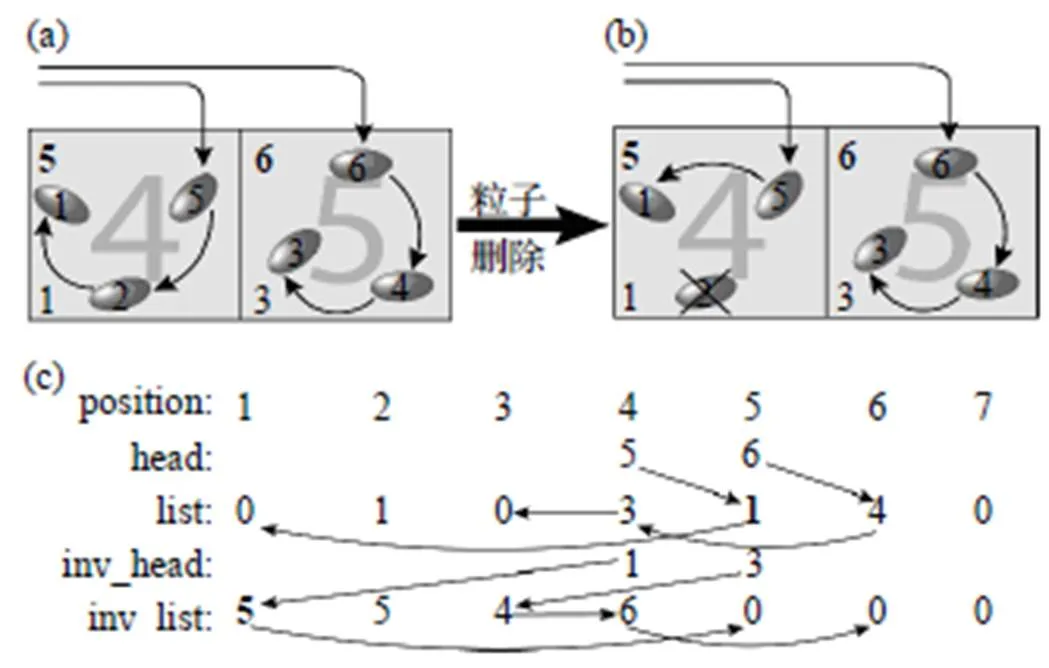
图2 元胞链表中的粒子删除
1.3 粒子插入
现在考虑粒子插入后如何更新链表. 例如, 在图3的元胞4中插入粒子7. 此时, 需要增加粒子7指向粒子5的箭头, 即list(7)=5, 并且粒子7成为起始粒子, 即head(4)=7. 在反向链表中, 粒子5指向7, 即inv_list(5)=7, 粒子7指向0, 即inv_list(7)= 0. 对于一般情况, 在元胞中插入一个粒子时, 插入前正向链表的头粒子是head(), 插入后变为了. 需要建立现头粒子和原头粒子的连接, 即list()=head(), 以及更改头粒子head()=. 对于反向链表, 插入前最后一个粒子head()需要指向插入粒子, 即inv_list(head())=, 并且粒子成为最后一个粒子, 即inv_list()=0.

图3 元胞链表中粒子插入
此外, 在元胞中不存在粒子的情况下, 插入的粒子也是反向链表的头粒子, 所以inv_head数组也将更改. 这些情况的具体实现详见算法5(表2).

表2 算法4、5的Fortran伪代码
1.4 Metropolis移动和非局域移动
图2和图3中数组的变化如图4所示, 黑体数字表示粒子插入删除前后变化的元素. 一旦通过元胞链表方法实现了粒子的插入和删除, 就可以利用此方法来实现Metropolis算法中粒子的随机移动(图5(a)), 以及其他蒙特卡罗方法中的非局域移动(图5(b~d)).
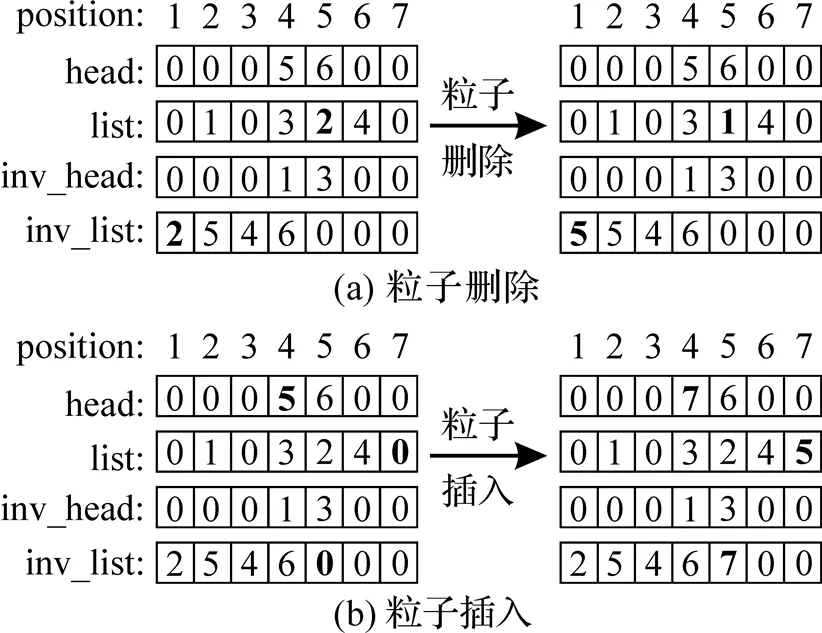
图4 粒子删除、插入的数组变化
对于Metropolis算法中粒子随机移动, 粒子从一个元胞移动到另一个元胞的情形如图6所示. 粒子从元胞4移动到元胞5(图6(a))可化归为在元胞4中删除粒子并在元胞5中插入粒子(图6(b)). 因此, 可以通过粒子删除和粒子插入的正向链表和反向链表的更新来实现Metropolis算法中粒子的随机移动. 同样, 对于绕枢轴转动或位形偏倚蒙特卡罗中的链回溯以及链再生, 可将其化归为粒子逐个删除和粒子逐个插入. 最后, 对于蠕动, 则可化归为一个末端的粒子删除以及另一个末端的粒子插入.
2 正确性和效率
现在来验证元胞链表方法的正确性. 采用元胞链表方法和Verlet列表方法分别模拟NVT系综中Lennard-Jones流体. 势函数选取为Lennard- Jones势, 其表达式为[1]:
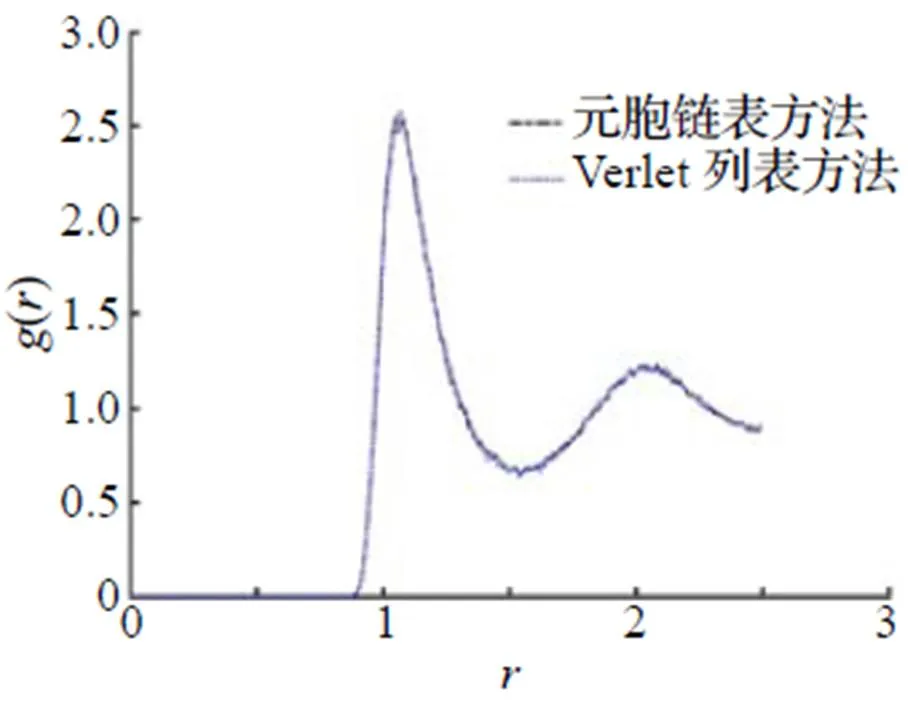
图7 Lennard-Jones流体在三相点附近的径向分布函数
另外, 还比较了状态方程. 体系的压强可以使用Virial公式[1]得到, 其形式为
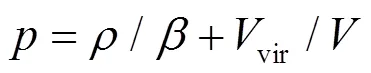
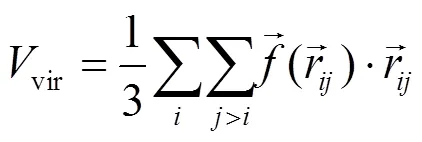
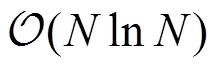
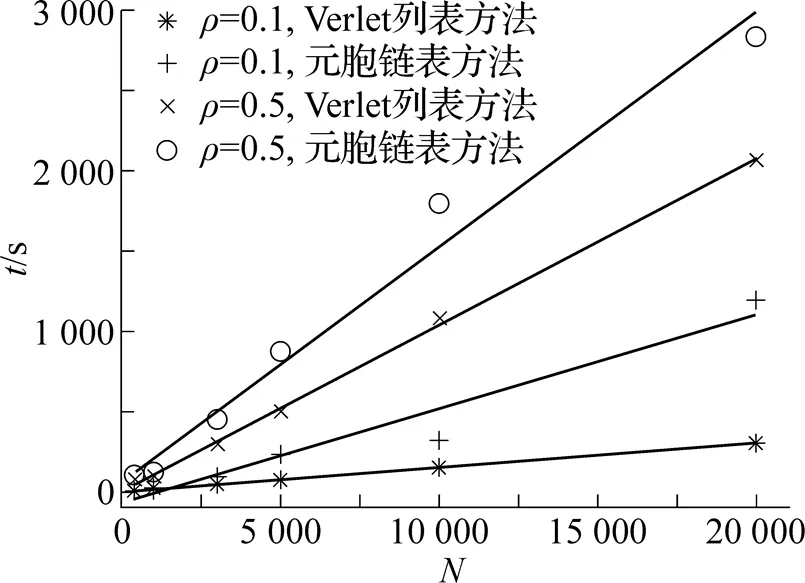
图9 不同粒子数时模拟10 000个蒙特卡罗步的时间
3 结论
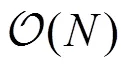
因为Verlet列表方法无法实现蒙特卡罗模拟中的非局域移动, 所以本文采用元胞链表方法实现了蒙特卡罗模拟中的非局域移动. 这是通过将这些移动化归为粒子的插入和删除过程, 进而使用双向链表来实现的. 此外, 还将该方法应用到Metropolis算法中的粒子随机移动, 这说明本方法也适用于Verlet列表方法能够适用的情形. 综上, 元胞链表方法的适用性比Verlet列表方法更广.
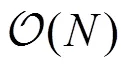
[1] Frenkel D, Smit B. Understanding molecular simulation: from algorithms to applications[M]. 2nd ed. San Diego: Academic, 2002.
[2] Allen M P, Tildesley D J. Computer simulation of liquids [M]. 2nd ed. Oxford: Oxford University Press, 2017.
[3] Hockney R W, Eastwood J W. Computer simulation using particles[M]. New York: McGraw-Hill, 1981.
[4] Heath Turner C, Brennan J K, Lísal M, et al. Simulation of chemical reaction equilibria by the reaction ensemble Monte Carlo method: a review[J]. Molecular Simulation, 2008, 34:119-146.
[5] Reed C E, Reed W F. Monte Carlo study of titration of linear polyelectrolytes[J]. The Journal of Chemical Physics, 1992, 96(2):1609-1620.
[6] Landsgesell J, Holm C, Smiatek J. Simulation of weak polyelectrolytes: a comparison between the constant pH and the reaction ensemble method[J]. The European Physical Journal Special Topics, 2017, 226:725-736.
[7] Carmesin I, Kremer K. The bond fluctuation method: a new effective algorithm for the dynamics of polymers in all spatial dimensions[J]. Macromolecules, 1988, 21: 2819-2823.
[8] Kremer K, Binder K. Monte Carlo simulation of lattice models for macromolecules[J]. Computer Physics Reports, 1988, 7:259-310.
[9] Sadus R J. Molecular Simulation of Liquids: Theory, Algorithms and Objection-Orientation[M]. Amsterdam: Elsevier, 2002.
[10] Siepmann J I, Frenkel D. Configurational bias Monte Carlo: A new sampling scheme for flexible chains[J]. Molecular Physics, 1992, 75:59-70.
[11] Mazzeo M D, Ricci M, Zannoni C. The linked neighbour list (LNL) method for fast off-lattice Monte Carlo simulations of fluids[J]. Computer Physics Communications, 2010, 181:569-581.
[12] Drozdek A. Data structures and algorithms in C++[M]. 4th ed. Boston: Cengage Learning, 2013.
[13] Welling U, Germano G. Efficiency of linked cell algorithms[J]. Computer Physics Communications, 2011, 182:611-615.
[14] Heinz T N, Hünenberger P H. A fast pairlist-construction algorithm for molecular simulations under periodic boundary conditions[J]. Journal of Computational Chemistry, 2004, 25:1474-1486.
[15] Gonnet P. A simple algorithm to accelerate the computationof non-bonded interactions in cell-based molecular dynamics simulations[J]. Journal of Computational Chemistry, 2007, 28:570-573.
[16] Mattson W, Rice B M. Near-neighbor calculations using a modified cell-linked list method[J]. Computer Physics Communication, 1999, 119:135-148.
Cell lists method based on doubly linked lists for Monte Carlo simulation
WANG Yimei, WANG Shaoyun, TONG Chaohui*
( School of Physical Science and Technology, Ningbo University, Ningbo 315211, China )
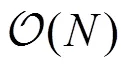
Monte Carlo method; nonlocal move; cell lists method; doubly linked lists
O411.3
A
1001-5132(2021)04-0086-07
2020−12−08.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
国家自然科学基金(21774067).
王逸梅(1994-), 女, 安徽淮北人, 在读硕士研究生, 主要研究方向: 高分子物理. E-mail: wangyimei0817@163.com
童朝晖(1968-), 男, 湖南常德人, 教授, 主要研究方向: 聚电解质理论. E-mail: tongchaohui@nbu.edu.cn
(责任编辑 韩 超)

