基于SAGA的工程项目资源均衡优化方法

李英攀，李亚峰，孙志凌，管 慧

(1. 武汉理工大学 土木工程与建筑学院， 湖北 武汉 430070；2. 中建三局第二建设工程有限公司， 湖北 武汉 430070)

工程项目资源优化可以使项目更合理、顺利地进行，合理的劳动力资源配置方案能够在保证项目工期的前提下，避免人员扎堆而增加施工现场人员管理成本，或者在有限的劳动力资源情况下，尽可能缩短工期，减少人工成本支出或获得提前竣工奖励，从而提高企业的经济效益，具有很强的实践意义[1]。由此可见，工程项目资源优化问题主要分为两类：“工期固定-资源均衡”问题和“资源有限-工期最短”问题[2]。本文拟先针对“工期固定-资源均衡”问题进行深入研究，该问题是典型的NP(Non-deterministic Polynomial)-hard问题，其求解难度和计算量随着工作或约束数量的增加而呈指数型增长，导致传统的甘特图分析、关键路径分析等人工计算方法的求解效率低下，并且其求解结果的最优性难以确定[3]。因此，粒子群优化算法[4]、遗传算法[5,6]、模拟退火算法[7]等机器学习算法在该问题上的应用被大量提出，用来避免传统方法繁琐的推断计算过程。但是，对比相关研究和大量重复实验发现，此类算法在应用中存在陷入局部最优的概率，即有概率只能得到次优的项目资源配置方案，不能达到资源均衡最优化的目的。

因此，本文拟开发一种应用于项目资源均衡优化问题的模拟退火遗传算法(Simulated Annealing Genetic Algorithm，SAGA)，以降低甚至消除陷入局部最优的概率，提高项目资源管理能力和资源使用效率。

1 SAGA理论基础

模拟退火算法(Simulated Annealing，SA)是一种基于蒙特卡罗迭代求解策略的一种随机寻优算法，模拟退火算法生成的随机解从较高初始温度出发，伴随温度的不断下降在解空间中寻找全局最优解[8]。与一般的寻优算法不同，模拟退火算法是以基于Metropolis准则的概率在邻域中寻找目标值较小的状态。同时，工程项目资源配置方案在一定范围内的小幅度变化，不一定会对目标值产生影响。因此，针对工程项目资源优化问题，模拟退火算法的全局寻优能力欠佳，比较容易陷入局部最优。

遗传算法(Genetic Algorithm，GA)将自然生物进化过程中的“优胜劣汰”作为寻优的基本思想，在全局范围内随机创建初始种群，根据种群中个体对环境的适应度大小对其进行选择，再通过交叉、变异等行为得到下一代，循环往复得到全局最优解[9]。但是，当种群内某个体适应度远高于其他个体时，该个体将难以得到进一步优化，从而可能导致算法过早收敛，陷入局部最优解。

模拟退火算法和遗传算法在单独使用时都可能陷入局部最优，但是，如果以模拟退火算法的重复寻优结果建立遗传算法的初始种群，避免随机创建初始种群时某个体适应度远高于其他个体的情况，就可以解决遗传算法陷入局部最优的问题[10]。在工程项目“工期固定-资源均衡”问题中，模拟退火算法的寻优结果是解空间内的最优解或者近似最优解，并且两者在目标值上的差异不大，不会导致遗传算法过早收敛，再通过遗传算法的进一步选择、交叉遗传可以得到其中的最优解，并且小概率的变异行为增加了解的多样性，增强了算法的全局意义。同时，模拟退火算法和遗传算法在优化机制、优化结构、优化操作等方面也具有较强的互补性或可融合性[4]，如表1所示。

综上所述，模拟退火算法和遗传算法的有机结合可以降低解决项目资源均衡优化问题时陷入最优解的概率，达到提高资源优化效率的目的。

表1 模拟退火算法和遗传算法的对比

2 工程项目资源优化模型构建

2.1 理论数学模型

工期固定的工程项目资源均衡优化问题的理论数学模型为：

(1)

s.t. ESn≤Tn≤LSn，n=1,2,…,N

(2)

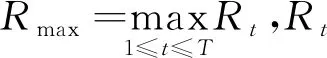
2.2 SAGA算法求解

(1)目标函数

由理论数学模型可知，目标函数由关键变量Rt计算得到，而Rt又受自变量Tn影响。因此，利用统一的数学语言表示Rt和Tn之间的关系是算法求解的前提。在“工期固定-资源均衡”问题中，关键线路是固定不变的，则自变量Tn实际是非关键工作的实际开始时间，N实际是非关键工作的总项数。

因此，建立非关键工作资源表示矩阵W(W=(wnt)N×T)：

(3)

式中：Rn为第n项工作的资源占用量；dn为第n项工作的持续时间。从而通过W列项求和可得到的T维行向量表示非关键工作的日资源占用量。而所有关键工作的日资源占用量是固定的，两者相加即为工程项目所有工作的日资源占用量Rt。至此，结合式(1)即构成算法求解的目标函数。

(2)SAGA算法求解

利用SAGA对上述模型进行求解，旨在通过SA对建立的随机工程项目资源配置方案进行优化，得到最优或次优资源配置方案。从而建立遗传算法的初始种群，再通过选择、交叉以及变异等遗传操作得到最优资源配置方案。SAGA算法优化工程项目资源均衡的步骤如下：

步骤1：导入数据与模型初始化。导入工程项目的相关数据，包括工期以及关键工作与非关键工作的最早开始时间ESn、最晚开始时间LSn、工作持续时间dn和资源占用量Rn。设置模拟退火算法相关参数，包括初始温度Tstart、终止温度Tend以及降温速率q等。设置遗传算法相关参数，包括种群大小popsize，迭代次数time，交叉概率Pc和变异概率Pv等。

步骤2：随机产生一个资源配置方案，记为S1。根据前文分析，该模型仅需随机产生一组符合最早、最晚开始时间要求的非关键工作开始时间即可：

S1n=round((LSn-ESn)rand+ESn)

(4)

式中：round为四舍五入函数；rand为在[0，1]区间内取随机数的随机函数。

步骤3：在S1基础上产生新的方案，记为S2。在S1中随机挑选一项工作a，并对该工作的开始时间进行随机提前或延后1 d：

S2a=S1a±1

(5)

同时，利用判断语句保证S2中非关键工作的开始时间始终符合其最早、最晚开始时间要求：若符合要求则进行步骤4；若不符合要求则重复步骤3，直至符合要求再进行步骤4。

步骤4：判断是否接受新方案。分别计算S1，S2的劳动力资源不平衡系数K1，K2，并以基于Metropolis准则的概率P接受S2。概率P的计算式如下：

(6)

步骤5：迭代优化。接受S2后，将S2赋予S1，重复步骤2～4。并进行降温，当温度低于终止温度时迭代结束，输出结果。

步骤6：建立遗传算法初始种群。重复步骤2～5，得到多组SA优化结果，作为遗传算法的初始种群，并进入遗传算法优化部分。

步骤7：编码。对SA结果组成的初始种群进行编码，实数编码具有染色体串短以及直接高效等优点，并且非关键工作开始时间只能是整数。因此，模型采用实数编码方式，每一个基因代表对应非关键工作的开始时间。

步骤8：选择-交叉-变异。模型采用锦标赛选择策略，即个体适应度越高越容易被选择作为父本产生下一代。交叉策略采用离散交叉，因为使用实数编码时，离散交叉比算术交叉收敛性强。此外，在没有特定需求的情况下，采用均匀变异概率是最可靠的[5]，变异策略与步骤3类似。

步骤9：迭代优化。根据迭代次数要求重复步骤8，对优化结果进行解码并输出最优解。

3 算例分析

为便于对比实验结果，验证SAGA算法的先进性，本文采用文献[1]中的工程项目资源案例进行优化求解。已知某工程项目的双代号时标网络计划如图1所示，横线上方为工作号，横线下方为工作持续时间，相关参数如表2所示。

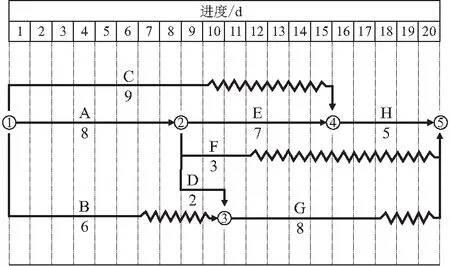
图1 算例双代号时标网络计划

由图1、表2可知，项目工期为20 d，并且工作A，E，H为关键工作，工作B，C，D，F，G为非关键工作，但工作D自由时差为0，没有可用的机动时间，因此，本例中仅需调整工作B，C，F，G的开始时间。在初始方案中，所有工作均按最早开始时间进行施工，此时日最高资源占用量Rmax=13人，资源不平衡系数K=1.512>1.5，该资源配置方案不可接受，需进一步优化。

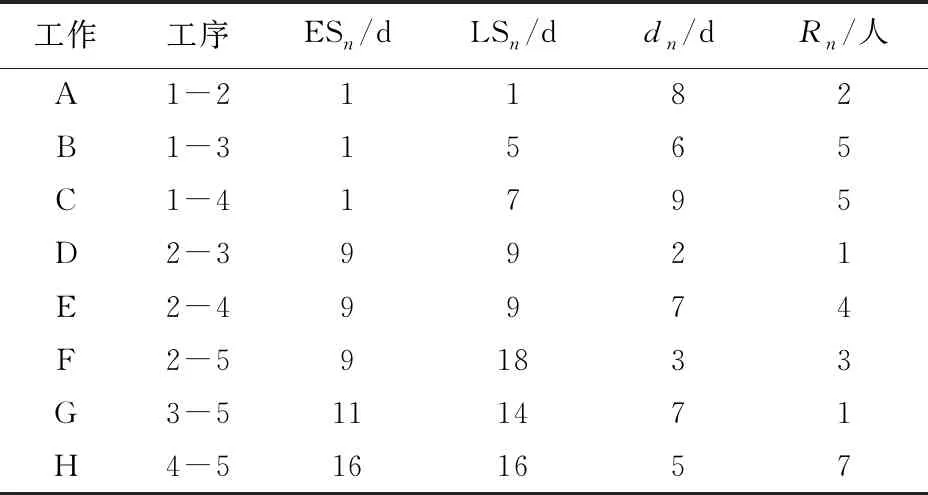
表2 算例相关参数

设置模拟退火遗传算法相关参数，初始温度Tstart=108，终止温度Tend=10-30，降温速率q=0.9，种群大小popsize=30，迭代次数time=50，交叉概率Pc=0.5，变异概率Pv=0.005。经过SAGA求解计算，得到非关键工作B，C，F，G的开始时间分别为1，7，18，11 h，资源不平衡系数最小，为1.163，满足小于1.5的要求，该资源配置方案可以接受。SAGA算法迭代优化过程如图2所示。

图2 迭代优化过程

模拟退火遗传算法相比于其他寻优算法的先进性不在于能够得到最优解，而是更小的陷入局部最优的概率。因此，分别采用GA，SA，SAGA算法对上述案例进行重复优化求解100次，并在优化程度、最优解稳定性和平均运行时间等方面进行对比，对比结果如表3所示。

表3 各算法重复优化结果对比

由于GA对工程项目的资源优化效果受种群大小影响，表中列出当遗传算法设置不同种群大小时的优化结果。随着种群大小的增加，算法运行时间增加，算法陷入局部最优概率减小。同时，最优解稳定性和种群大小之间是凸性函数，即虽然增加种群大小可以增加最优解的稳定性，但是种群越大，优化效率越低。仅使用SA对工程项目进行资源优化，其最优解稳定性和运行时间方面的表现均欠佳，不能满足实际优化需求。而SAGA在资源优化过程中，能够用较小的种群，在较短的运行时间内得到100%稳定的优化结果，工程项目资源优化效率和稳定性极佳，具有极高的指导实践能力。

4 结 语

(1)基于对模拟退火算法和遗传算法的搜索能力、优化机制、优化结构和优化操作互补性和可融合性的分析，将两者有机结合，利用模拟退火算法优化结果作为遗传算法初始种群，降低了遗传算法由于某个体适应度远高于其他个体导致的过早收敛概率，增强了算法的全局搜索能力。

(2)对模拟退火算法产生新解方式和遗传算法的变异策略进行重新设计，建立了适用于工程项目资源均衡优化问题的模拟退火优化算法。通过算例验证，相较于GA和SA，SAGA在最优解稳定性和运行时间方面的综合表现更优秀，大大提高了资源优化效率。

(3)SAGA算法能够有效解决项目资源优化中的“工期固定-资源均衡”问题，在下一步的研究中，拟选取合适的算法解决“资源有限-工期最短”问题，同时考虑工期奖惩制度，寻找资源配置和工期之间的最佳平衡点，完善项目资源优化应用体系。