二维平板水漂运动数值模拟
付晓琴,李阳辉,卢昱锦,肖天航,童明波
南京航空航天大学 航空宇航学院,南京 210016
长期以来,对于水漂运动的机理研究及应用已深入到诸多领域。在炮弹领域,为了能够避开防鱼雷网而轻松摧毁目标,参照二战时期航空工程师Barnes Neville Wallis设计的“跳弹”,Johnson[1]提出,通过分析炮弹撞击角度和弹射速度范围,能够实现不断在水上弹跳进而躲避防御的方案。航天方面,宇宙飞船的返回舱再入大气层时,通过控制其与大气层的接触角度,产生“弹跳”的运动过程,能达到降温的效果[2]。同样,在水陆两栖飞机领域,为了保证飞机着水安全性与稳定性[3-4],该问题显得尤为重要。较差的触水姿态可能会导致飞机在着水时发生“海豚运动”或者跳跃现象[5-6]。因此,对水漂运动的研究具有一定的工程应用价值。
面对水漂这一物理现象,Rosellini[7]、Lyderic[8]以及Clanet[9]等开展了大量的试验研究,借助高速摄像机记录圆盘水漂运动过程不同时刻的姿态与水面变化,探究其中的流体机理与力学性能,结果表明当圆盘与水面的夹角大约为20°时,圆盘打水漂所需的初始投掷速度最小,并且由于圆盘的高度自旋使得姿态角变化不明显。此外,Rosellini等[7]还通过简单的单体理论预测石头的运动,分析石头在打水漂过程中受到的重力以及冲击过程中石头表面的压力,证明在高速旋转的情况下,石头的反弹是由水动力响应引起,在运动过程中的速度衰减和相对能量损失与自身姿态角有关。理论分析结果虽然与试验结果相差不大,但在分析过程中忽略了冲击时水体的运动,在压力计算中面积多是采用与流体接触的石头面积近似值。Lyderic等[10]则提出了石头与水碰撞过程的简化物理模型,依然不考虑由于石头运动导致的流体运动,结果表明石头完成水漂的最大次数与自身速度衰减和稳定性有关。通过增大石头的初始速度可以实现多次的反弹。另外,保持石头的高度自旋有利于自身的稳定性。Do等[11]利用一种基于物理建模的水漂运动仿真方法分别计算水对石头的作用力和水的变形,得到石头水漂的运动轨迹。球体能在水面反弹存在一个最大的入射角,如果撞击速度足够大,速度与入射角之间的关系可以用一个简单的常微分方程模型(Ordinary Differential Equation, ODE)[12-13]来表达。Nagahiro等[14]将ODE模型应用到圆盘水漂冲击中,求得圆盘能弹跳的最小速度和最大投掷角度的解析解。戴岩伟[15]同样借助水漂运动的物理模型,计算触水过程中石头受到的浮力和阻力,并从能量消耗的角度分析石头能弹跳的最小速度和最大投掷角度。理论分析通常采用简化模型,得到的结果与实际情况有一定差异。近年来,更多的探索工作集中在水漂运动的数值模拟研究。Nagahiro等[14]使用光滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)方法对Clanet等提出的最佳攻角、最小投掷速度和最大投掷角度进行数值仿真,计算结果与试验值相吻合。Yan和Monaghan[16]采用相同的方法对二维平板水漂运动过程进行数值模拟,论证了三维运动与二维运动的相似性,讨论不同姿态角、投掷角和底面形状的平板对水漂运动的影响。邬明[17]和陈诗伟[18]利用任意拉格朗日-欧拉(Arbitrary Lagrange-Euler, ALE)法对圆盘击水弹跳现象展开研究,分析入水角、俯仰角、初始速度和旋转角速度的相关性。面对水漂运动可能发生的多次弹跳,SPH和ALE方法需要构建相当大的计算域,使得计算成本过高,效率低。
本文应用体积分数 (VOF) 模型结合整体动网格方法对二维平板水漂运动进行数值模拟,加入了有限体积法的优势,规避了多次弹跳过程导致的数值水池区域过大的问题,在实现精确捕捉水面的同时提高了计算效率与精度。确定能完成水漂运动的最小投掷速度和最大投掷角度,并从能量损失的角度分析不同姿态角、投掷角、投掷速度对水漂运动的影响,从动量变化的角度探究发生“弹跳”的原因。进而,引入速度入口造波法研究波浪水面水漂运动过程,掌握平板运动姿态和能量变化在同一波形不同位置和不同波高工况下的运动规律,为水陆两栖飞机着水或类水漂运动的研究工作提供技术支持和数据支撑。
1 数值计算方法
对于平板水漂运动的数值模拟计算方法主要包括以下4个部分:流体控制方程及求解,自由液面捕捉方法,速度入口造波方法,整体动网格方法。流体控制方程主要为数值模拟提供理论支持,自由液面采用VOF方法进行精确捕捉,波浪数值水池的建立依赖速度入口造波法,整体动网格方法最终实现平板运动过程的模拟。
1.1 流体控制方程求解
流体控制方程为非定常雷诺平均Navier-Stokes(URANS)方程,湍流模型选用k-εRNG。SIMPLE算法用于求解压力-速度耦合计算;有限体积法实现控制方程对空间的离散;在时间离散中,采用格林-高斯格点方法求解梯度,选择PRESTO!离散压力项;利用几何重构方法描述体积分数;其余均选用二阶迎风格式离散。
1.2 自由液面捕捉方法
在研究刚体与水面撞击的过程中,对于水面变化和液体飞溅的精确捕捉有利于还原实际的物理过程,同时提高仿真结果的准确性。VOF方法可以实时追踪自由液面的形状和位置,利用网格单元中流体体积和网格单元自身体积的比值函数来确定自由液面的状态[19]。比值函数范围为0~1。数值为0则表示此网格不存在该流体,数值为1说明此网格被该流体充满,数值介于0~1为自由液面。
1.3 速度入口造波方法
速度入口造波方法是将波面方程(式(1))和水质点速度(式(2))施加在速度入口边界。随着计算时间的推进,波浪从入口向计算域远场传播开来。为了避免波浪传播到计算域出口产生反射波,对平板黏性流场和运动的计算产生影响,需要将压力出口边界附近的一段区域设置为阻尼消波区。文献[20-21]中采用速度入口造波法数值模拟了线性规则波与不规则波,与试验结果吻合。该方法的造波精度论证工作在前期已经完成[22-23],这里不做赘述。本文采用线性规则波实现平板在波浪水面水漂运动的数值模拟。波浪参数及波形位置说明如图1所示,波面方程表达式为
(1)
式中:η为波面高度;H为波高;x为水质点的x坐标;k为波数;ω为圆频率。
波浪中水质点(x,y)的水平速度分量u与垂直速度分量v的表达式为
(2)
式中:φ为速度势函数;T为周期;d为水深;θx为波浪传播方向与x轴正向的夹角。
阻尼消波采用动量源项消波的方法,对于距离压力出口位置两个波长的长度区域进行消波,消波方式为在动量方程中增加动量衰减项[22],其表达式为
(3)
式中:x0为在消波区中的计算域x坐标。消波区示意如图1所示,可以看到,添加动量衰减项之后,波幅明显变小。
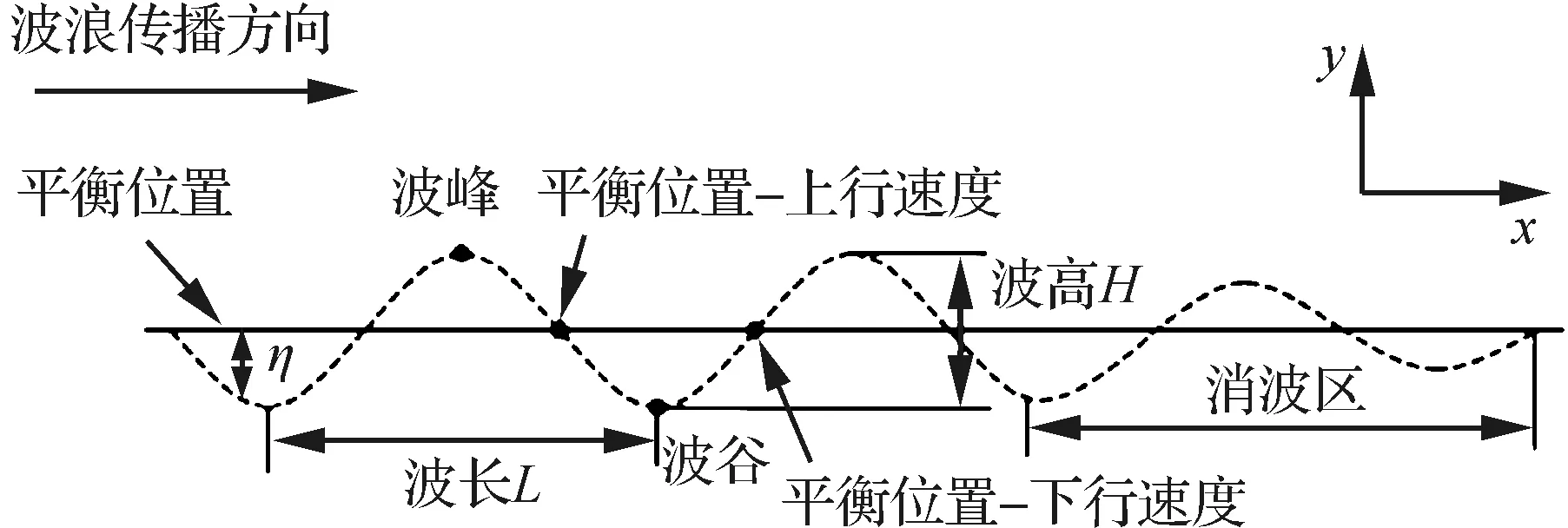
图1 波浪参数与波浪不同位置
1.4 整体动网格方法
整体动网格方法是一种在物体运动过程中将整个计算域(包括网格单元和边界)与物体相固连的方法,即整个计算域与物体有相同的运动规律[24]。在两相流计算中,由于网格区域跟随物体一起运动,为了保持水面位置不发生变化。需要对边界条件进行特殊处理。在静水面的计算中,水面保持固定高度,需给定合理的体积分数边界条件,将水面之上的部分赋予空气的属性,水面之下的部分赋予水的属性。在波浪水面的计算中,保证波浪平衡位置为一定值,速度入口边界的波面高度随时间做余弦函数变化,以维持稳定的波形。在体积分数边界条件的设置中,水的体积分数α1∈[0,1]。通过判定当前网格与水面位置的关系,给出合理的体积分数。α1=0表示网格中水体积分数为0,此网格在水面上方;α1=1表示网格中水体积分数为1,此网格在水面下方;α1=0.5表示网格中水体积分数为0.5,此网格为水气交界面。通过对网格的分类,实现不同介质的压力初始化。位于水面以上为空气域,压力即为大气压101 325 Pa,位于水面以下为水域,压力与深度成正比,P=ρghw,其中,g=9.8 kg/m2,ρ=998.2kg/m3,hw为当前网格与水面的垂直距离。此方法在课题组之前的工作中已经取得良好的成果[22-23]。
2 数值模型与网格设置
2.1 平板水漂模型
参照Rosellini等[7]的水漂试验圆板尺寸构建数值模拟的二维平板模型。采用的二维铝制板如图2所示,其中,α为平板姿态角,β为平板投掷角,R为平板半长度,h为平板厚度,U为投掷速度。该平板长度L为2R=50 mm,厚度为h=2.75 mm。
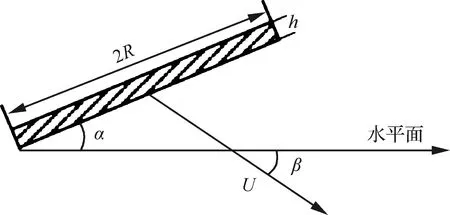
图2 二维平板模型
2.2 网格划分
为保证远场不受影响,计算域长为16L,高为10L。采用结构网格划分流场计算域,如图3(a)所示。为了更精确地捕捉水气两相流的情况,同时考虑到平板在运动过程中垂向位移较大,需要对平板与水面附近区域的网格进行局部加密,垂向加密区宽度为2L(-0.07~0.03 m)。根据k-ε湍流模型适用的y+值的范围为30~300,得到最小网格尺寸为0.000 2 m。取网格增长率为1.2,实现加密区的网格向外围网格的光滑过渡,得到最大网格尺寸为0.006 m,网格量约为13万。静水面工况计算域边界条件的设置如图3(b)所示,平板表面为无滑移壁面边界。在波浪水面的数值模拟中,由于波浪传播到计算域出口会产生回流,为了避免对流场造成影响,计算域长为30L,高为10L,网格划分与上文一致,边界条件如图3(c)所示。
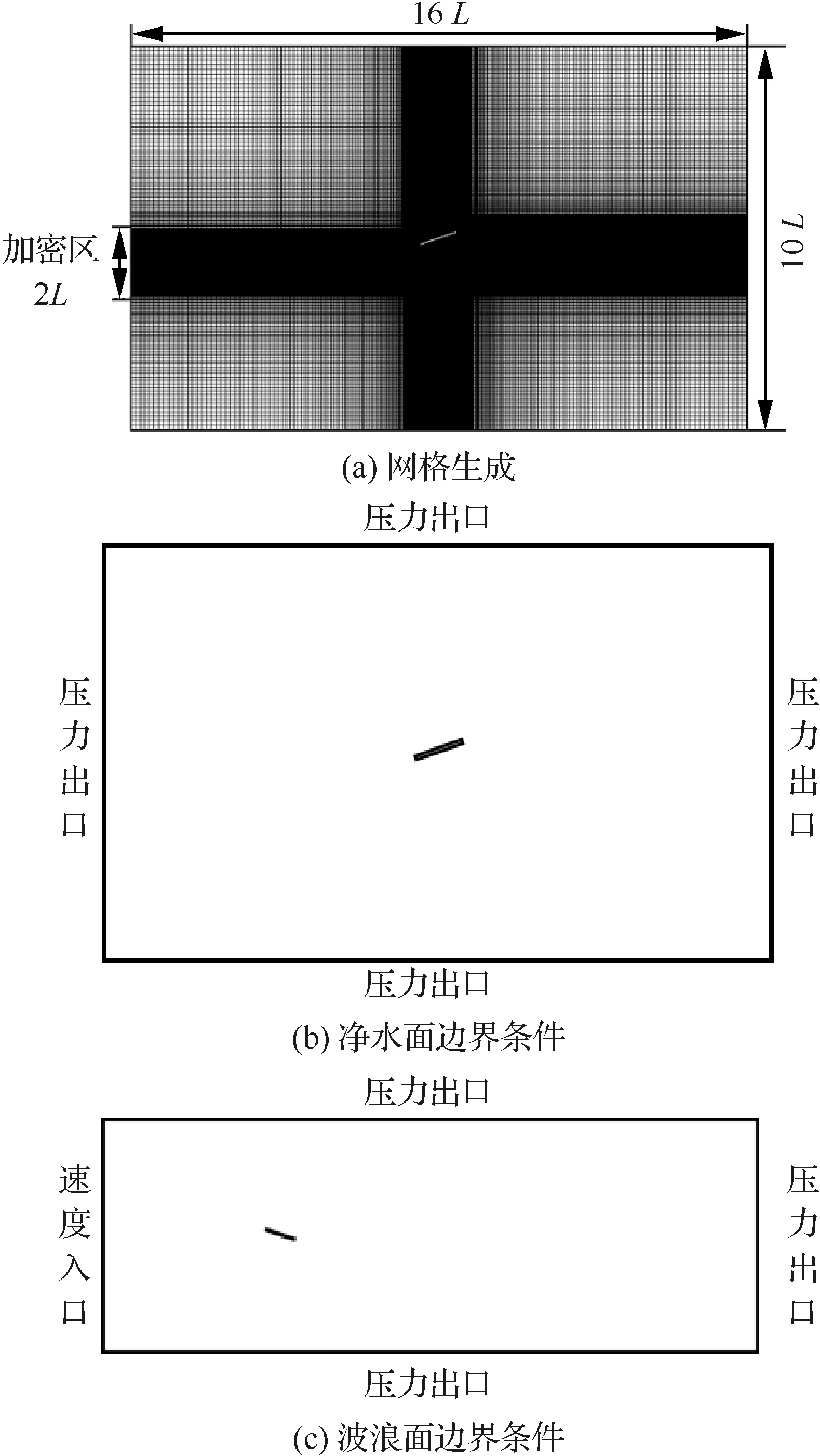
图3 二维网格与边界条件
3 算例验证
为了验证数值方法及整体动网格技术在平板水漂数值模拟过程中的可行性和准确性,采用文献[7]中的平板水漂试验进行算例验证。计算域x、y向尺寸与二维网格一致,z向长度为10L;采用全结构网格划分,最小网格尺寸为0.000 2 m,网格增长率为1.2,得到的总网格量约为470万,如图4(a)所示。边界条件设置与坐标轴的定义如图4(b)所示,平板初始最低位置与水面重合,通过数值模拟得到三维圆板在不同姿态角下能完成水漂运动所需的最小速度与最大投掷角。在最小速度的计算过程中,平板投掷角为20°;在数值模拟最大投掷角时,平板投掷速度为3.5 m/s。
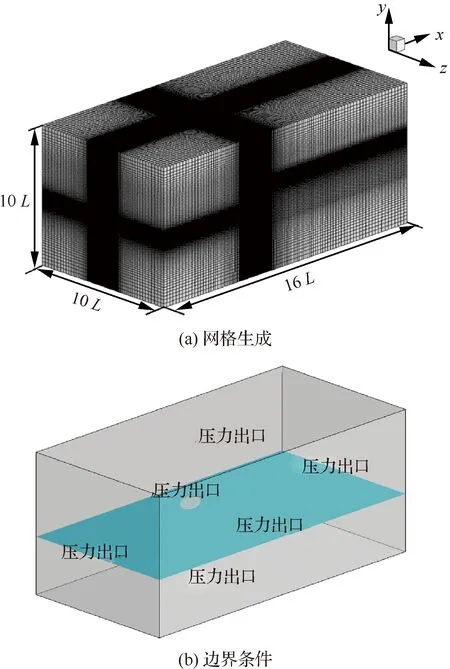
图4 三维网格与边界条件
图5(a)给出平板完成水漂运动所需最小投掷速度Umin的数值模拟结果与试验值[6]和理论解[14]的对比。可以看出,数值模拟值与试验值相比偏小,但一直都在理论值A和B之间,三者具有相同的变化规律。具体来看,当a<5°时,数值模拟得到的最小速度比理论值A、B和试验值低,随着α的增大,数值模拟得到的最小速度与试验值逐渐接近,直到α>20°时,数值模拟值与理论值A和试验值吻合度越来越高。同时,通过数值模拟可以看出,当平板姿态角为20°左右时,其能进行水漂运动所需的投掷速度最小,这与试验得到的结论相吻合。
图5(b)给出平板能进行水漂运动的最大投掷角度βmax的数值模拟结果与试验值[7]和理论解[14]的对比。可以看出,数值模拟值与试验值和理论值具有相同的变化规律,虽然相比试验值稍大,但一直在理论值A、B形成的区域内。具体表现为,当姿态角较小时,数值模拟得到的值与理论值B吻合度较高,与试验值相比偏大;随着姿态角的增大,开始与理论值A和试验值相吻合。
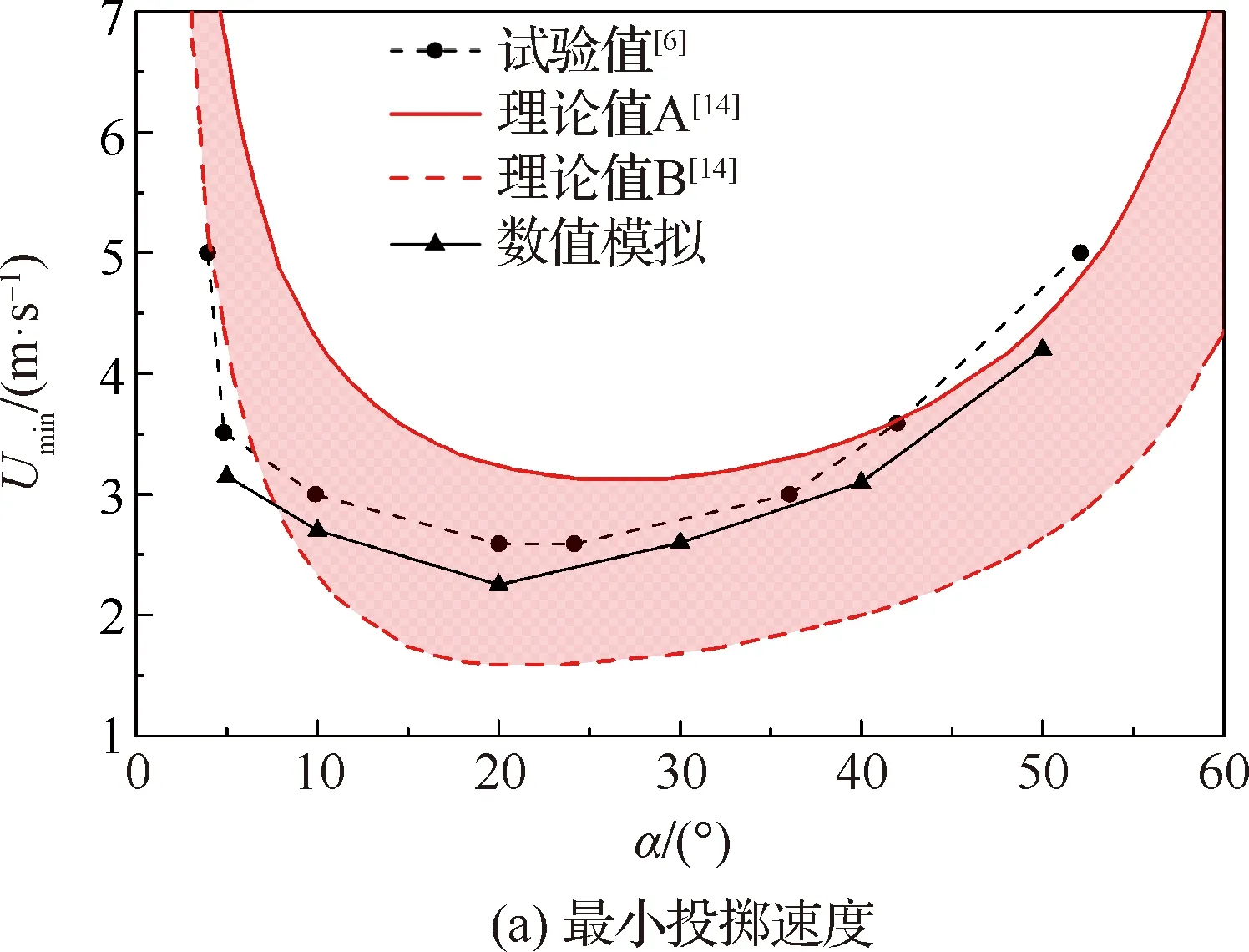
图5 数值模拟与试验值和理论值对比
出现上述现象的原因是:当平板以较小的姿态角触水时,与水面的夹角较小,平板下方的空气容易被压入水中,导致明显的空气垫[25]现象。空气破碎形成气泡容易造成水面的变形,它的状态与流动形式不稳定,其中水气比例不断变化,很难采用合理的理论模型与数值模拟方法进行准确的描述,因此导致数值模拟得到的结果在小姿态角的条件下与试验值和理论值具有一定差距。当平板姿态角增大时,在平板下方的空气更容易逃逸,空气垫现象不明显,此时数值模拟得到的值与试验值和理论值A误差更小。考虑到网格精度有限,数值模拟得到的值与试验值和理论解仍然有所差别。但总体来看,数值模拟的结果与试验值和理论解有相同的变化规律,且误差在可接受范围内。
4 二维与三维平板的运动特性相似性
本文主要对二维平板进行水漂运动数值模拟,在外形上与实际三维圆板有所区别,故需要对二维与三维平板的运动特性相似性进行说明。
平板与水面接触碰撞期间,流体作用力是决定平板能否反弹的重要因素,根据平板垂向动力学方程:
(4)
(5)
式中:Fz为垂向流体作用力;Swet为平板触水面积;CL为升力系数;CD为阻力系数,令Cn=CLcosα-CDsinα,其只与模型形状和α相关,由于水漂运动选用的α较小,故Cn为常数。
分3种情况对Swet进行讨论:三维圆板、三维方板、二维方板;其中,圆板直径、三维方板底部边长以及二维方板边长均为2R,三者高度均为h。
Swet=
(6)
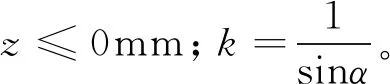
由式(6)可知,当模型为三维和二维方板时,Swet与z呈线性关系;当模型为三维圆板时,Swet与z呈非线性关系。如图6所示,为R∈[15 mm,30 mm],α=20°的三维圆板Swet与z的关系曲线簇。
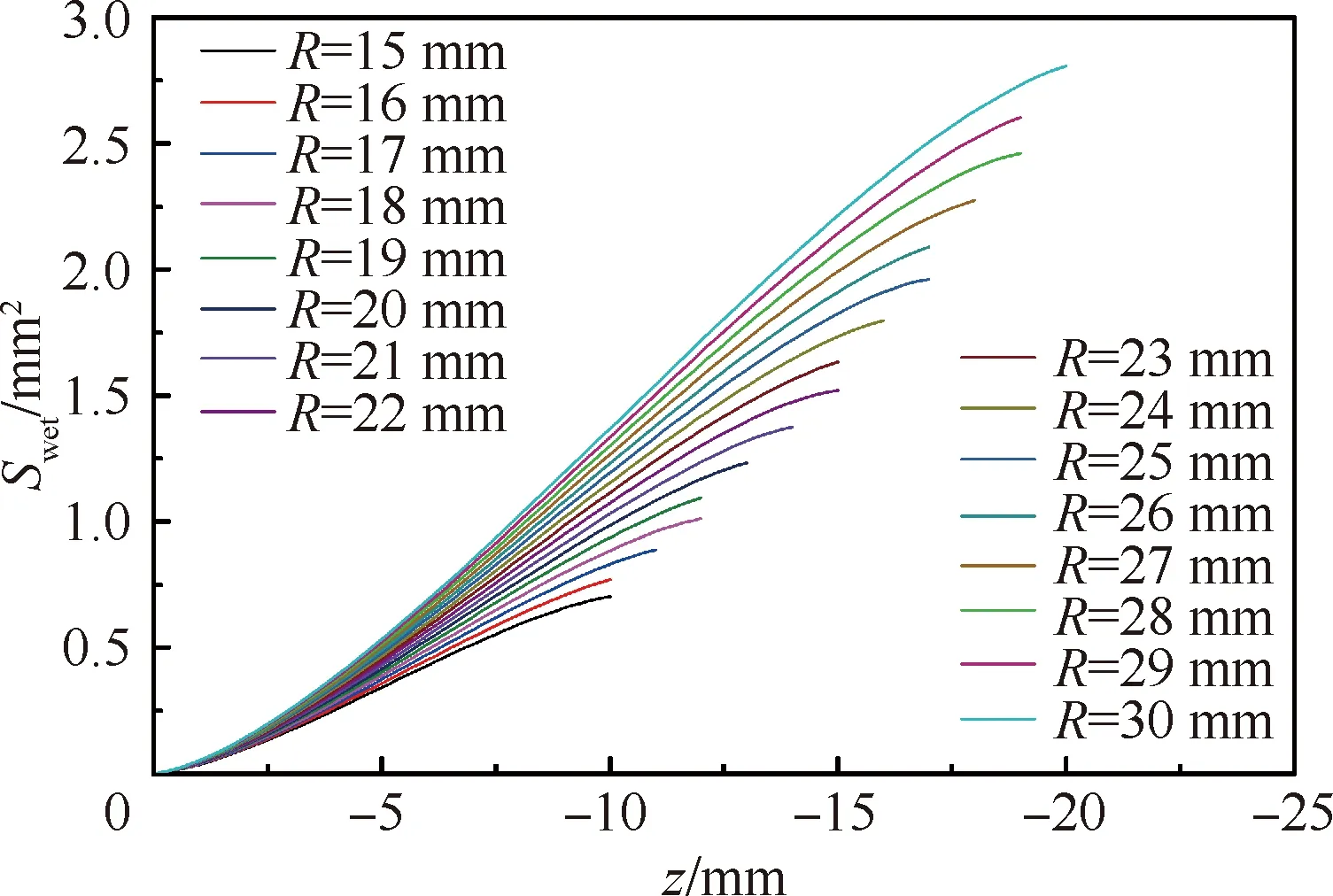
图6 α=20°时Swet与z的关系曲线
利用多项式线性拟合可以得到Swet与z的近似线性关系式:
Swet≈-(1.779 7R)kz-0.174 6R2-
0.916 4R+7.107
(7)
对原始曲线和拟合曲线在R∈[15 mm,30 mm],α∈[10°,30°]范围内进行拟合优度计算,得到的决定系数r2>0.995,决定系数r2[26-28]越接近1代表两条曲线吻合程度越高;故式(7)能很好地代替式(6)中的三维圆板关系曲线。
以R=25 mm,α=20°为例,Swet的理论曲线与通过式(6)得到的拟合曲线的决定系数r2=0.995 7, 曲线如图7所示,在初始触水与触水到最大深度时,拟合曲线与理论曲线有一定误差;在其他位置,该线性曲线可以很好地描述圆板实际触水的运动特征。
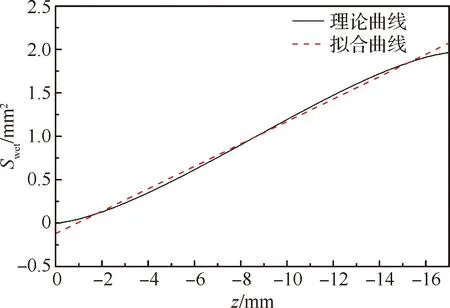
图7 Swet与z的理论与拟合曲线
当模型为圆板时,Swet与z的关系式为
Swet≈-0.889 85(L/sinα)z+φ
(8)
式中:L=2R;φ=-0.174 6R2-0.916 4R+7.107。
综上,
(9)
故式(4)可以改写为
(10)
式中:q为常数项,
其中:Cn1、Cn2、Cn3为常数,由物体形状决定。
因此,式(10)为受定值外力作用的简谐运动方程式,可以改写为
(11)
(12)
其中:
代入式(12),得到
(13)
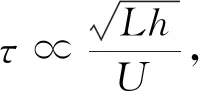
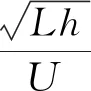
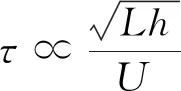
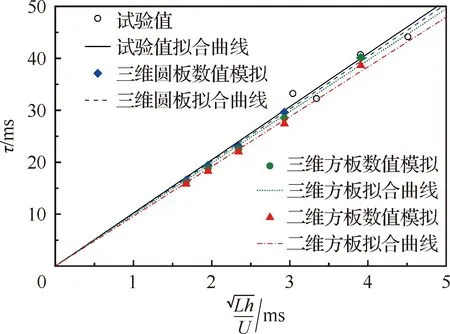
图8 触水时间τ随的变化曲线
5 计算结果及分析
5.1 二维平板静水面水漂数值模拟
参照文献[16],由于平板在水漂过程中高速自旋,姿态角α在整个碰撞过程中保持不变,因此在数值模拟过程中只放开x方向与y方向平移自由度。本节通过改变平板初始姿态角α、投掷角β、投掷速度U对平板水漂运动过程进行数值模拟。计算直到平板沉入水中。模型如图2所示。通过分析平板水平速度、垂直速度、垂直位移、能量变化,确定上述参数对平板水漂运动过程的影响。能量仅考虑平板机械能,其定义为
(14)
式中:E为物体机械能;m为物体质量;U为运动速度大小;g=9.8 kg/m2;H为高度差。
5.1.1 姿态角α的影响
平板投掷角为20°,投掷速度为4 m/s,初始时刻平板最低点与水面重合。数值模拟α=10°,20°,30°时平板的水漂运动。图9为不同姿态角的平板第1次水漂运动过程中不同时刻的水面变化,可以看出,随着姿态角的增大,平板触水时形成的水面凹陷越大,其前端形成的射流越大,完成一次水漂的耗时更长。
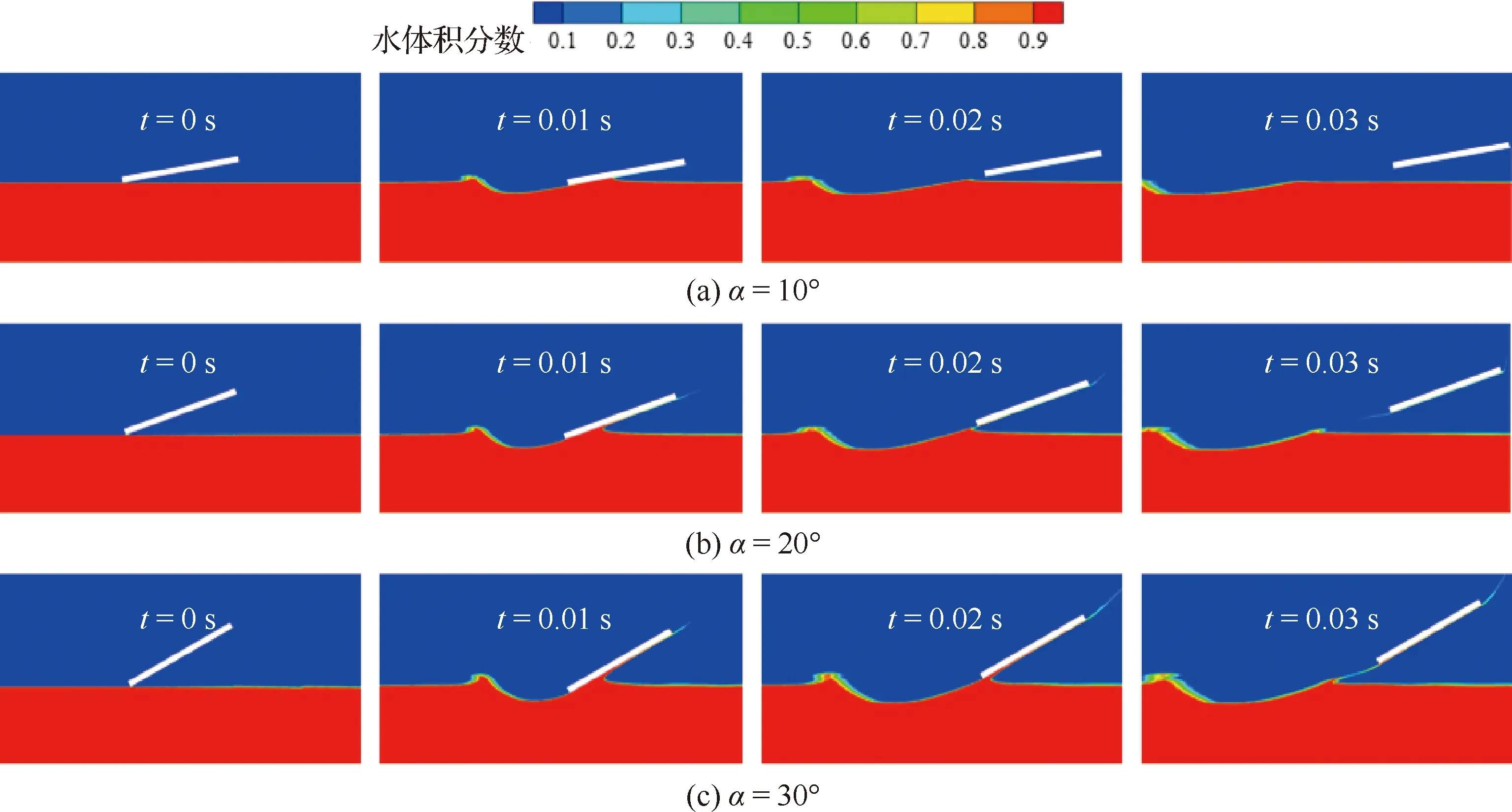
图9 不同姿态角条件不同时刻水面变化
不同姿态角的平板在水漂运动过程中速度变化曲线以及平板重心位置的垂直位移和能量变化曲线见图10。如图10(a)所示,平板在触水的过程中,水平速度持续衰减。随着姿态角的增大,水平速度衰减幅度增大。此外,图10(b)垂直速度变化曲线与图10(c)垂直位移变化曲线显示:在第1次水漂运动的过程中,姿态角越大,平板垂直速度变化范围越大,反弹的高度也就越高。而后续过程,垂直速度变化范围逐渐缩小,图10(d)给出平板水漂运动过程的能量变化曲线,表1反映了不同姿态角的平板在前3次触水过程中的相对能量损失:
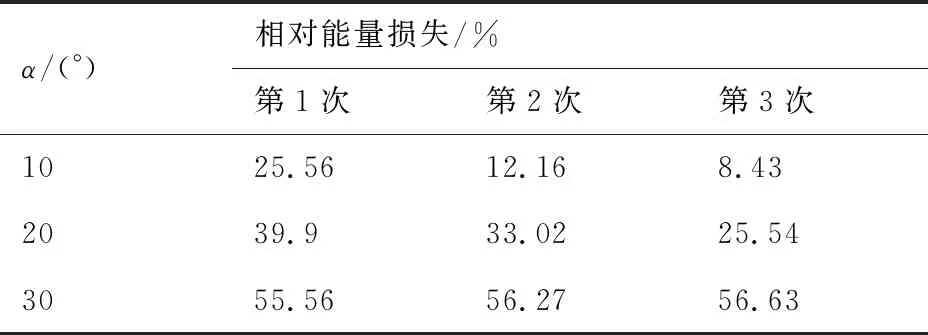
表1 不同姿态角平板前3次水漂运动相对能量损失
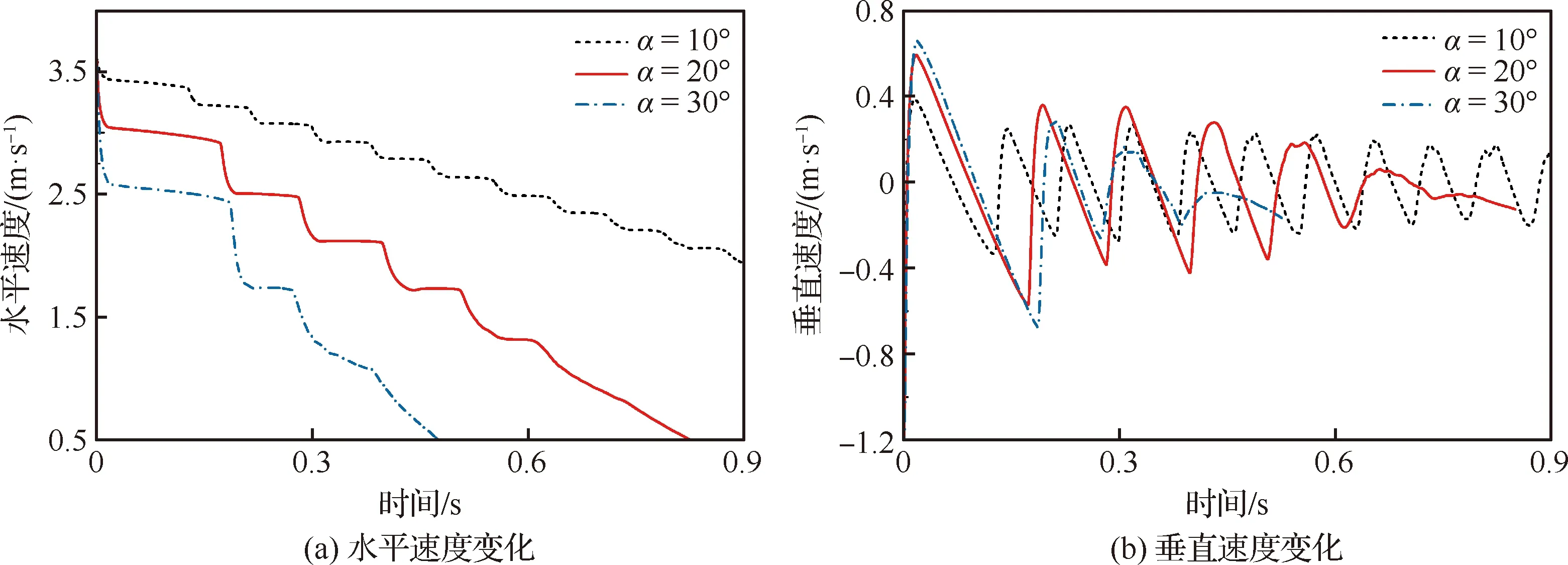
图10 不同姿态角条件对比曲线
显然,姿态角越大的平板,一次水漂运动过程的相对能量损失越大。当姿态角从30°减小到10°,在第1次水漂运动的过程中,相对能量损失从55.56%降低到25.56%。同时,姿态角为10°、20°的平板在后续的运动过程中,相对能量损失呈现递减趋势,而姿态角为30°的平板相对能量损失基本不变,导致30°姿态角的平板水漂次数要小于其余两个姿态角的平板。分析原因:姿态角小的平板在触水后,与水接触面积迅速增大,导致升力增大,平板在入水过程中减速的更快,平板浸水深度小,在水面向前运动所需推动的流体量小,所受到的阻力小,能量的损失小。平板在水漂运动过程中能否从水面弹起取决于在外载荷作用下的y方向动量改变量,即y方向外载荷F对平板的冲量。根据冲量的定义:
(15)
不同姿态角下,平板质量m相同,入水时y向速度Uy1相同,故出水时y向速度Uy2只与冲量相关。图11给出平板在水漂运动过程中受到的冲量变化,可以看到,在第1次水漂运动时,10°姿态角的平板所受到的冲量最小,仅为30°姿态角的78%左右,故平板出水速度小,从水面反弹的高度也相应变小。而姿态角越大,平板完成一次触水过程的所受冲量大,因此出水速度大,平板能弹起更高的高度;但平板初始触水时,与水面小的接触面积导致的小升力使得平板更容易浸入水中,产生更大的附加质量,能量损失有所增大。当姿态角过大时,能量损失过大引起水平速度快速衰减,垂直速度变化范围迅速变小,平板无法离开水面,很快沉没。综上所述,对比3个不同的姿态角,可以看出以相对能量损失最小的10°姿态角进行水漂运动可以得到最多的水漂次数。

图11 y方向冲量变化曲线
5.1.2 投掷角β的影响
平板姿态角固定为20°,投掷速度为4 m/s,初始时刻平板最低处与水面重合,对比分析投掷角β=10°,20°,30°时的仿真结果,总结出投掷角对平板水漂的影响规律。图12为不同投掷角的平板第1次水漂运动过程中不同时刻的水面变化情况。可以看出,采用相同的平板,投掷角较小时,平板触水深度小,在运动过程中激起的水花也小,平板很快从水面反弹。而当投掷角较大时则相反,更容易在平板前部形成射流,激起的水花更多,完成一次水漂的耗时也相对较长。
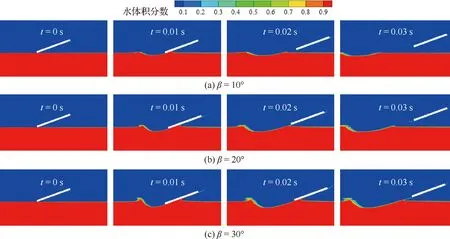
图12 不同投掷角条件不同时刻水面变化
图13给出不同投掷角的平板在水漂运动过程中速度变化的曲线以及垂直位移和能量变化曲线。如图13(a)所示,投掷角越大,平板在水漂运动过程中水平速度衰减幅度越大。图13(b)垂直速度变化曲线与图13(c)垂直位移变化曲线表明,更大投掷角度使平板拥有更大的垂直速度,导致平板浸没深度更大。这意味着在水漂过程中平板会产生更大的附加质量和能量损失。在完成第一次水漂后,20°投掷角的平板反而是弹起高度最高的。反映在能量损失方面,如图13(d)和表2所示,投掷角越大的平板在第1次水漂过程入水深度也越大,由于附加质量的原因,平板消耗在水中的能量也越大。当平板投掷角β从10°增加到30°,在完成第1次水漂后,相对能量损失从24.59%上升到57.75%。正因如此,投掷角β=10°的平板虽然垂直方向速度最小,但得益于其每次相对能量损失为3种工况中最小,因此实现的水漂次数最多。
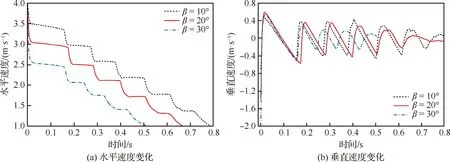
图13 不同投掷角条件对比曲线
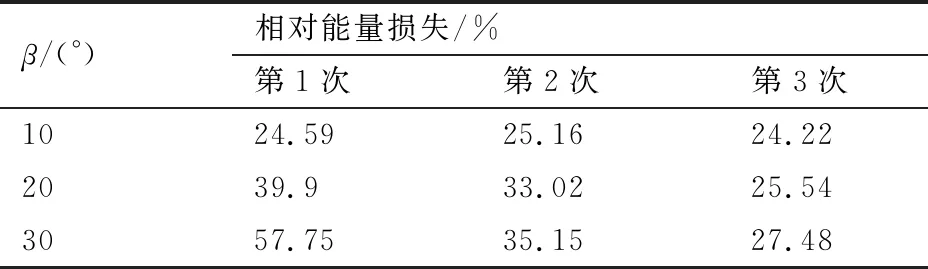
表2 不同投掷角平板前3次水漂运动相对能量损失
5.1.3 投掷速度U的影响
平板姿态角为20°,投掷角为20°,初始时刻平板最低点与水面重合,分析对比U=3,4,6 m/s时的仿真结果,得到投掷速度对平板水漂的影响。图14分别不同投掷速度的平板第1次水漂运动过程中不同时刻的水面变化。投掷速度小的平板在水漂运动过程中水面形成的凹陷小,在运动过程中所激起的水花与平板前端的射流不明显;当投掷速度变大时,水面形成的凹陷变大,在运动过程中所激起的水花与平板前端的射流变得明显。
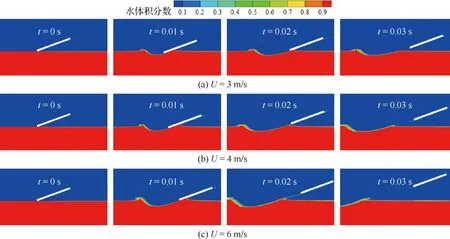
图14 不同投掷速度条件不同时刻水面变化
不同投掷速度条件下平板在水漂运动过程中速度变化曲线以及垂直位移和能量变化曲线如图15所示。图15(a)水平速度变化曲线显示平板投掷速度越大,初始水平速度越大,衰减的程度趋于一致,因此投掷速度小的平板更快停下来。图15(b)垂直速度变化曲线与图15(c)垂直位移变化曲线表明,平板投掷速度越大,初始垂直速度越大,导致平板在水面反弹的高度高,完成一次水漂运动的时间长。从图15(d)平板水漂运动过程的能量变化曲线以及表3中平板前3次水漂运动的相对能量损失数值可以看出,在第1次水漂运动的过程中,投掷速度大的平板的相对能量损失略小于投掷速度小的平板。具体而言,平板速度大小从速度为3 m/s增加到6 m/s时,相对能量损失从41.27% 下降到38.75%。在后续水漂运动的过程中,相对能量损失的比例也都维持在30%左右。分析原因:由于平板的初始速度有差异,投掷速度大的平板初始水平速度与垂向速度大,因此在水漂运动过程中,平板的垂向速度与垂向位移变化范围大。而根据伯努利定理,水平速度大的平板在触水时带动附近的水运动,与下层静水面的压差大,造成平板在触水时受到的升力大,平板在垂向的加速度大,减速更快。但正是由于此时初始垂直速度也大,因此投掷速度对触水深度影响不大,相对能量损失随其变化规律也不明显。且对比前两个工况,平板初始能量相等,改变投掷速度时,平板的初始能量存在差异。投掷速度越大初始能量较多,而每次水漂运动的相对能量损失比例相当,因此投掷速度小的平板在水面水漂运动的次数更少。综上所述,投掷速度大的平板能完成更多次数的水漂运动。
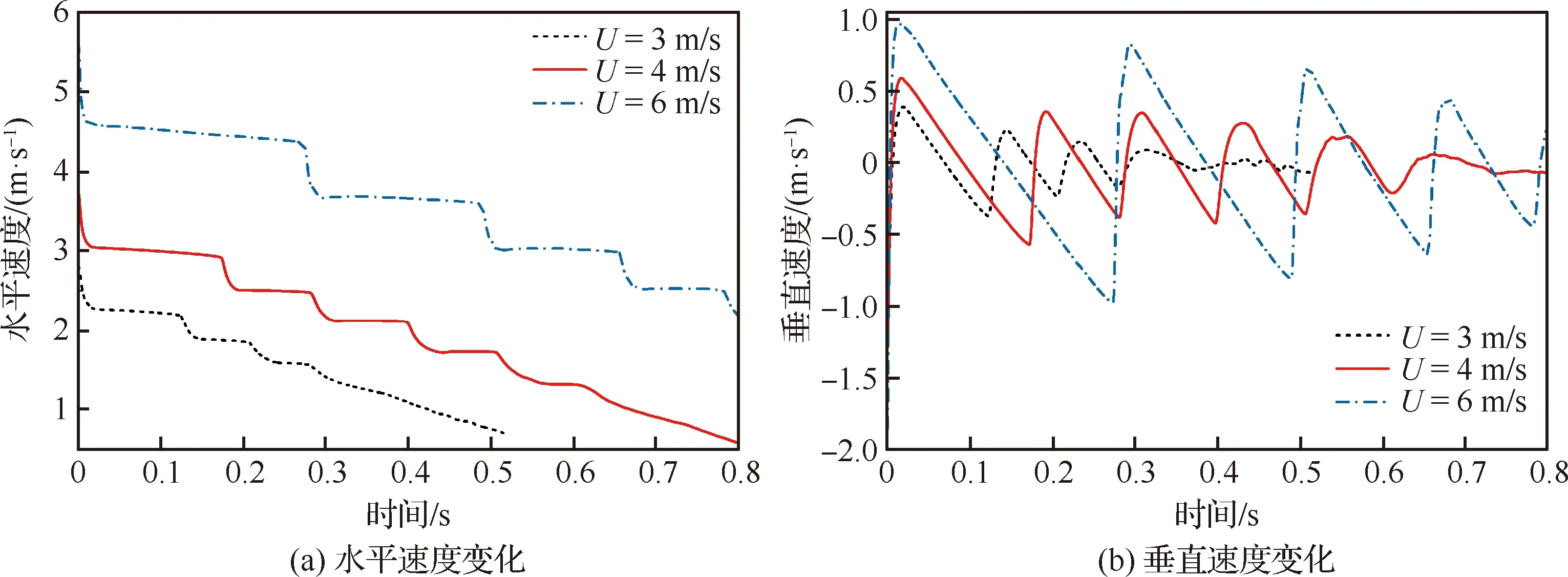
图15 不同投掷速度条件对比曲线
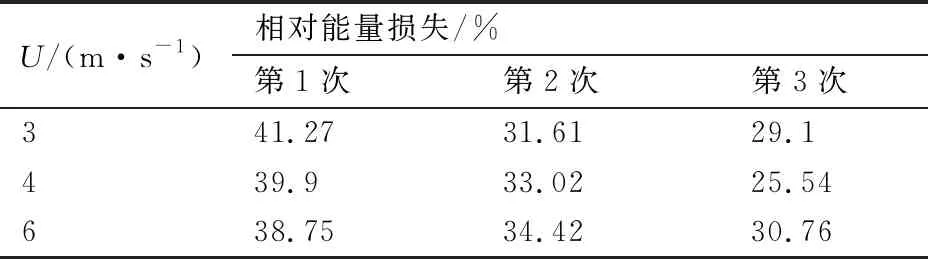
表3 不同投掷速度平板前3次水漂运动相对能量损失
5.2 二维平板波浪水面水漂数值模拟
平板在波浪水面水漂运动时,从水面弹起后无法预测下一次触水点的位置,因此本节重点研究平板在波浪水面的第1次水漂过程,讨论不同相位位置和不同波高对平板水漂运动的影响。
5.2.1 同一波形不同相位触水对平板水漂运动的影响
在波浪条件下,由于平板姿态角为20°,计算得到平板在垂向投影长度为0.017 m,为了防止波高太高,平板直接冲入水中,无法离开水面,因此选择线性规则波浪参数为:波高H=0.02 m,波长l=0.3 m。利用速度入口造波法得到的波浪初始水面如图16所示。初始时刻模型最低点与波浪相应位置重合。计算过程中平板姿态角α=20°,投掷角β=20°,投掷速度大小U=4 m/s,波浪从左向右传播,平板迎浪投掷。选择波峰、波谷、平衡位置-上行速度和下行速度4个触水位置(见图1) 数值模拟平板第1次水漂运动过程。

图16 波浪初始相位
图17为平板在波浪水面的不同位置第1次水漂运动的水面变化情况。可以看出,平板在波峰触水与水面撞击形成的凹陷最小,在波谷处最大。在波谷位置和波浪平衡位置-上行速度位置触水的平板,需要跟随波浪运动到波峰才能离开水面。
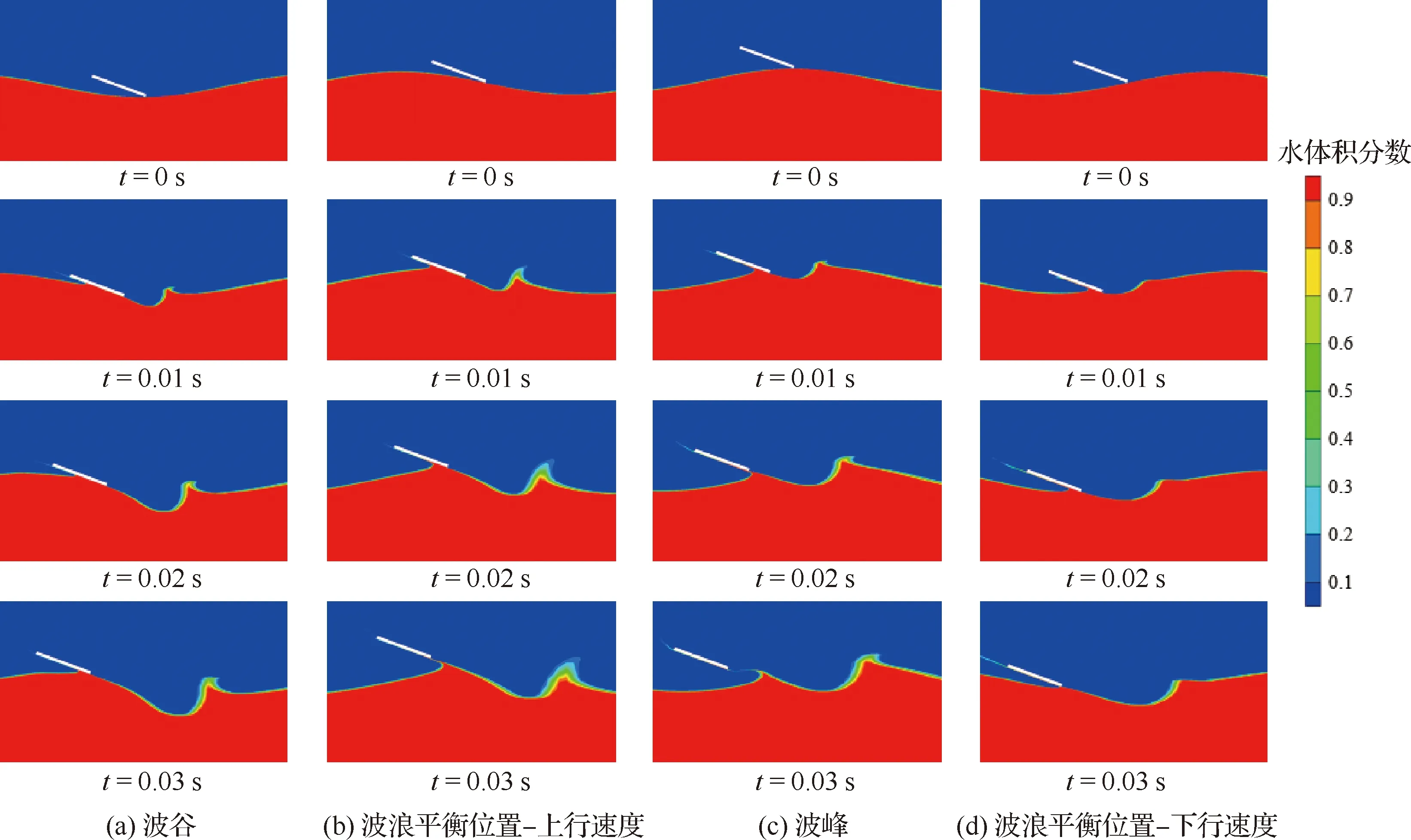
图17 平板在波浪不同位置触水时水面变化
图18给出平板在波浪不同位置触水时的速度、垂直位移以及平板能量变化曲线。可以看出,平板在波浪水面水漂运动与在静水面水漂运动有相似的运动趋势。在第1次水漂运动的过程中,不同触水位置水平速度衰减由大到小依次为波谷、波浪平衡位置-上行速度、静水面、波浪平衡位置-下行速度、波峰位置。其中,最大衰减幅度约为25.5%,最小约为 14%。对于垂直速度的变化,却呈现出与水平速度近乎相反的规律,在波谷处触水的平板最大垂直速度可达到1.2 m/s,在波峰处触水的平板仅约为0.2 m/s。因此导致不同位置触水的平板从水面反弹的高度差异巨大。图18(d)以及表4从能量角度解析平板运动特征的差异。平板在波浪水面水漂时,除波峰位置触水的相对能量损失较小,其余条件下相对能量损失大致相似,在40%左右,与5.1节静水面条件下水漂运动相对能量损失相似。具体来看,在波浪平衡位置-上行速度触水的平板相对能量损失最大,约占40.95%,波峰处最小,仅为最大值的86.8%左右。分析原因:平板所有的能量损失可以理解为水漂过程中水相获得的能量。平板与水相的能量交换与平板和撞击点波浪运动切线的夹角θ以及接触时间有关,其中,夹角θ的定义如图19所示,夹角越大,平板触水的面积越大,受到的阻力越大,导致水平方向速度衰减幅度大,造成更多的能量损失;对于上述4个触水点位置,在波浪平衡位置-上行速度触水,此时平板迎浪撞击波面,与波浪切线的夹角接近180°,因此导致其相对能量损失大;当平板在波峰处触水时,与波浪接触的时间最短,同时接触面积也较小,造成平板的能量损失小;在波浪的波谷位置触水时,虽然此时夹角不是最大,由于波浪和平板存在相对运动,平板必须贴着波面运动到波峰位置,与水面的接触时间最长,导致平板的能量损失较大。最终呈现出上述运动姿态与能量变化规律。
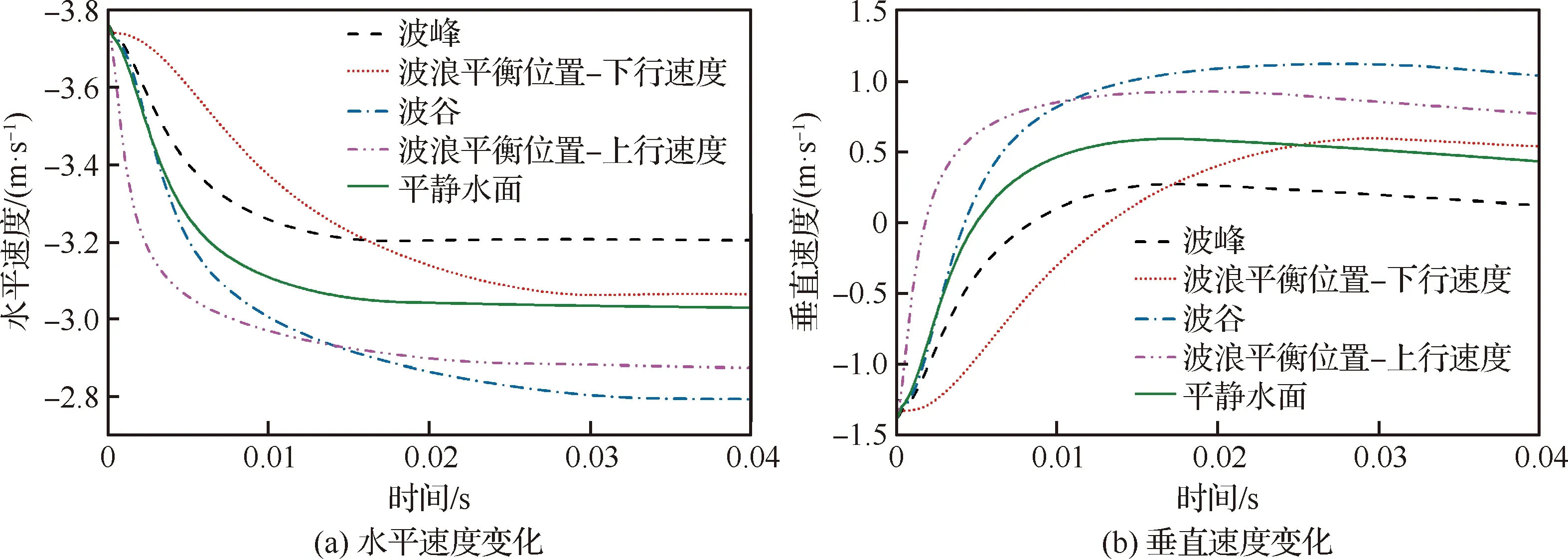
图18 波浪不同位置触水对比曲线

表4 平板在不同位置触水的相对能量损失
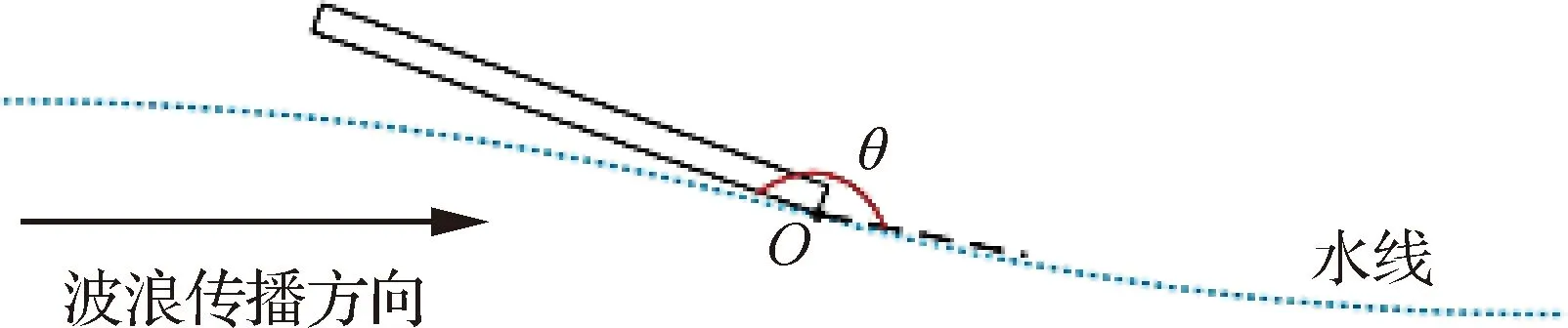
图19 平板和波浪在撞击点切线的夹角
5.2.2 不同波高同一触水位置对平板水漂运动的影响
参照5.2.1节得到的结论,选择能量损失最大的波浪平衡位置-上行速度与能量损失最小的波峰位置触水,通过改变波高为0.01 m、0.02 m、0.03 m,实现在不同波高对于平板水漂运动的影响。
1) 波浪平衡位置-上行速度触水
图20给出不同波高条件下在波浪平衡位置-上行速度触水的水面变化图。不同波高明显改变了水与平板的接触面积,且平板均随波浪运动到波峰位置才能离开水面。
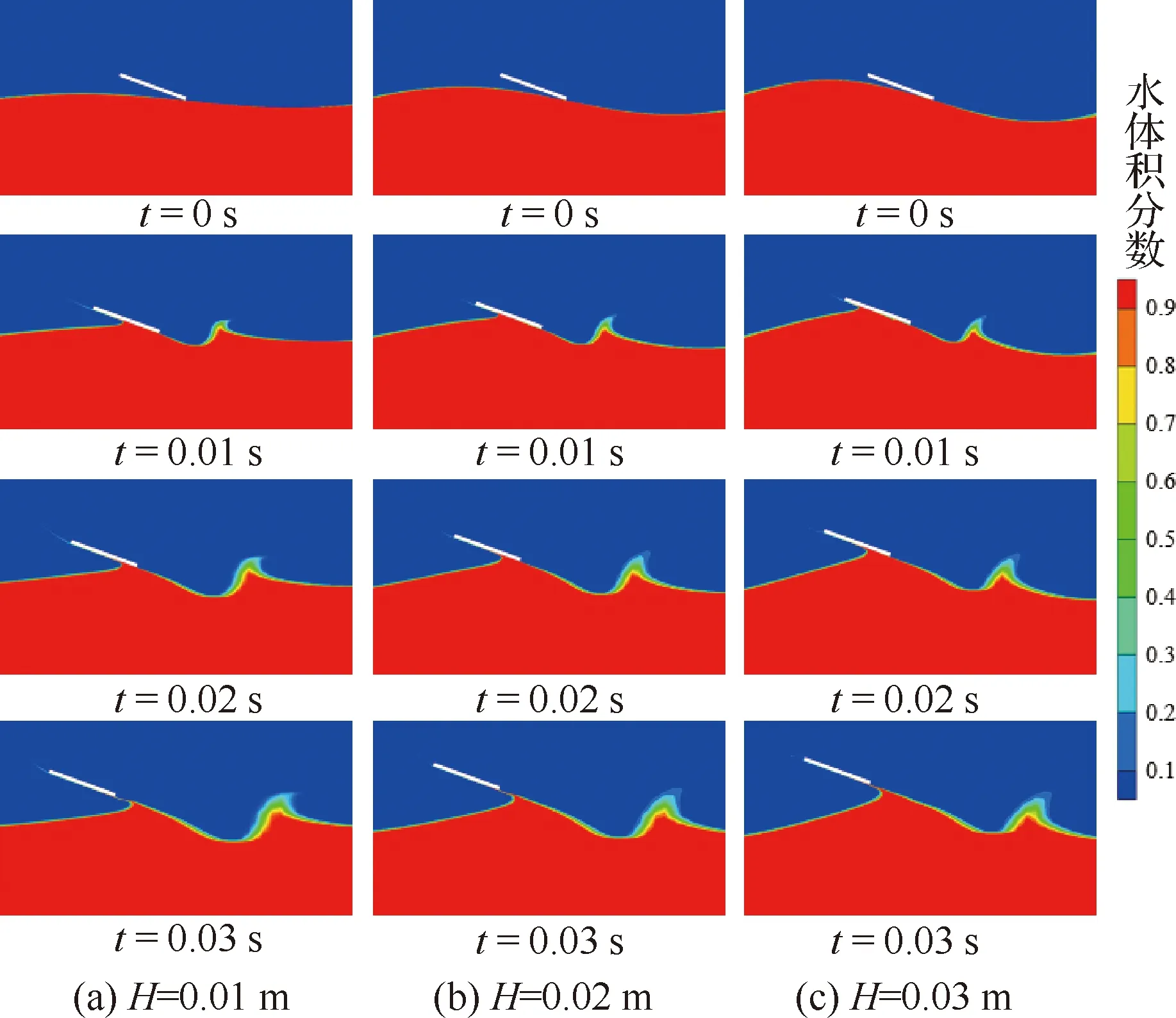
图20 平衡位置-上行速度触水水面变化
平板在不同波高的波浪平衡位置-上行速度触水时的速度、垂直位移和能量变化曲线见图21。可以看出,平板运动姿态和能量的变化与波高线性相关,但影响不大。在波高为0.01 m的波形触水,平板水平速度衰减最小,约为23.6%,垂直速度变化量最小,约为2.17 m/s,相对应的垂直位移也最小,此时的相对能量损失约为39.1%。随着波高的递增,水平速度衰减幅度增量约为1.99%,垂直速度变化增量在0.07 m/s左右,相对能量损失增量约为1.35%。分析原因:不同波高参数改变了平板与接触点波浪运动切线的夹角。当平板在波浪平衡位置-上行速度触水时,波高越高,意味着平板与波浪切线的夹角越大,此时平板触水时与水面贴合的更好,接触面积更大,因此平板水平速度衰减幅度更大,由于此时受到的垂向力更大,平板能反弹更高的高度。同时,平板在此处触水后需要运动到波峰的位置才能离开水面,因此在波高越高的工况下平板完成一次水漂运动的触水时间长,造成的相对能量损失也就相应更大。
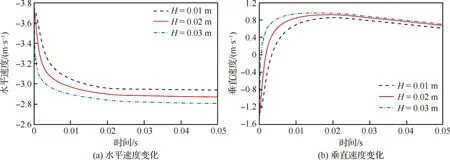
图21 平衡位置-上行速度触水变化对比曲线
2) 波峰位置触水
图22给出不同波高条件下在波浪波峰位置触水的水面变化图。可以看出,不同波高条件下平板水漂运动时水面形成的凹陷大致相同。平板从触水到离水的时间随着波高的增加而变小。
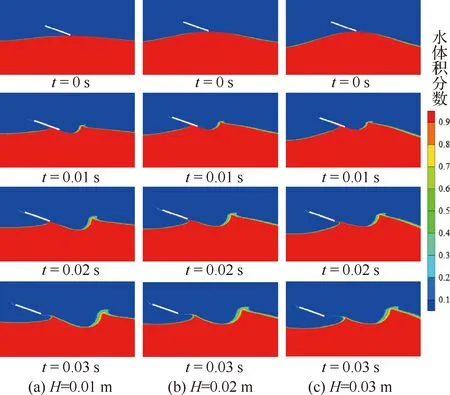
图22 波峰位置触水水面变化
图23为平板在波高为0.01 m、0.02 m、0.03 m的波浪波峰触水时的速度、垂直位移和能量变化曲线。可以看出,其变化趋势与波浪平衡位置-上行速度位置触水相反,且受波高影响更明显。其中,在波高为0.01 m的波形触水,平板水平速度衰减最大,约为17.5%,垂直速度变化量最大,约为1.928 m/s,相对应的垂直位移也最大;此时相对能量损失约为37.8%。随着波高的递增,水平速度衰减幅度减小约4%,垂直速度变化减小值在0.25 m/s左右,相对能量损失减小值约为2.36%。分析原因:波高参数越大,波浪越陡,波峰形状也更尖锐。因此,在波高越高的波峰位置触水时,平板越容易离开水面,由于接触的时间短,平板水平速度衰减幅度小,能量损失也就相应的变小。同时由于越尖锐的波峰位置处波浪内流速度变化越小,平板在触水过程中受到的冲量小,导致垂直速度变化小,垂直位移相应变小。
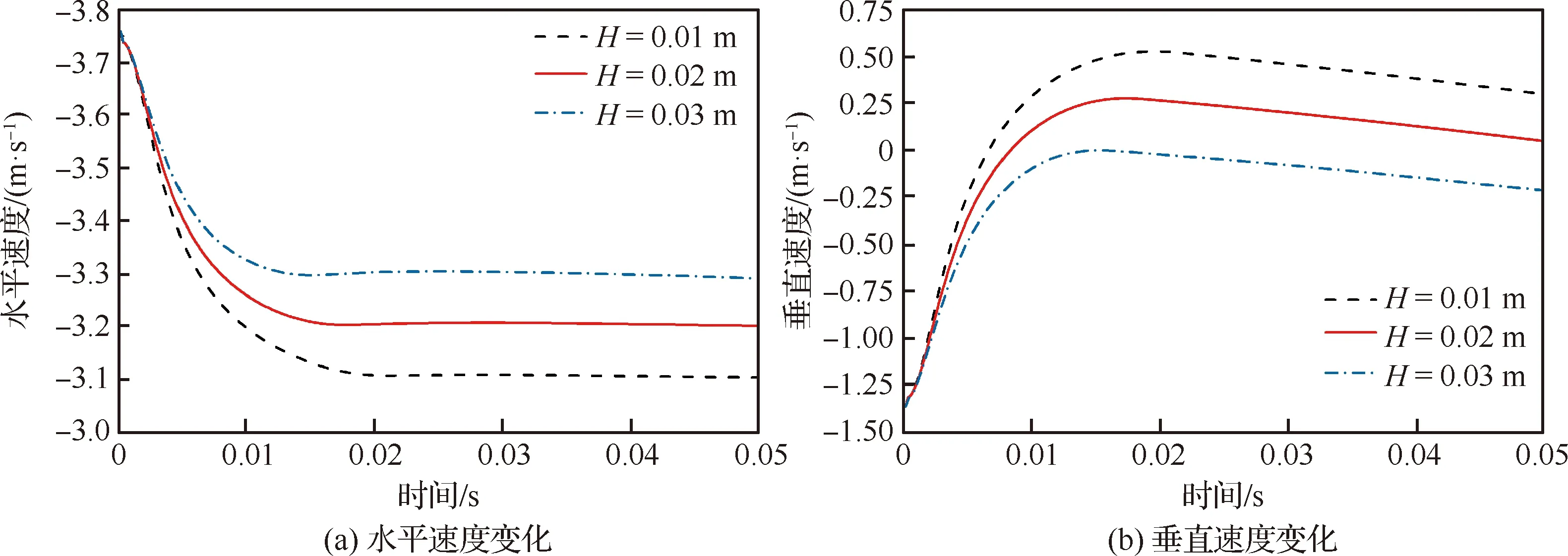
图23 波峰位置触水变化对比曲线
6 结 论
1) 采用整体动网格结合VOF方法可以对平板水漂运动过程进行很好的数值模拟,计算得到的结果与试验值和理论值的误差均在合理范围内。
2) 当姿态角为20°左右时,平板能以最小的投掷速度完成水漂运动。当投掷速度一定时,姿态角为10°的平板的相对能量损失小,随着投掷角的增大相对能量损失也随之增大,因此10°姿态角的平板水漂运动的次数最多;平板投掷角与投掷速度也影响着水漂运动的次数,投掷角为30°的平板相对能量损失最大,随着投掷角的减小,平板的相对能量损失减少,水漂运动的次数增多;投掷速度则影响平板的初始能量。投掷速度越大,平板初始能量越大,虽然相对能量损失比例相当,投掷速度大的平板可以完成更多次数的水漂运动。
3) 研究平板在波浪水面不同位置触水时,在波浪平衡位置-上行速度触水的平板相对能量损失最大,约为40.95%,其次为在波谷触水,上述两种条件均比在相同条件下的静水面工况的相对能量损失大。在波浪平衡位置-下行速度位置触水的相对能量损失较小,最小发生在波峰位置触水,仅为最大值的86.8%左右。这是由于不同的触水位置决定着平板与水面的接触面积和触水时间,接触面积越大,触水时间越长,相对能量损失越大。
4) 探究波高对平板水漂运动的影响,平板运动姿态与能量损失与波高线性相关。波高对平板在波浪平衡位置-上行速度触水影响较小,当波高为0.01 m时,平板水平速度衰减最小,约为23.6%,垂直速度变化量最小,约为2.17 m/s,相对应的垂直位移最小,相对能量损失约为39.1%。随着波高的递增,水平速度衰减幅度增量约为1.99%。垂直速度变化增量在0.07 m/s左右,相对能量损失增量约为1.35%。波高对平板在波峰位置触水影响稍大,且与在波浪平衡位置-上行速度触水工况的规律相反。当波高为0.01 m时,平板水平速度衰减最大,约为17.5%,垂直速度变化量最大,约为1.928 m/s,相对应的垂直位移也最大,相对能量损失约为37.8%。随着波高的递增,水平速度衰减幅度减小约4%。垂直速度变化减小值在0.25 m/s左右,相对能量损失减小值约为2.36%。

