基于Copula函数的三峡库区万州段蓄水前后降雨量-径流量关系分析

王晓菊，毛海涛,2，黄庆豪，程龙飞

(1.山西农业大学 城乡建设学院，山西 太谷 030801；2.武汉大学 水利水电学院，湖北 武汉430072)

1 研究背景

三峡水库自2003年蓄水以来，改变了库区内水文循环的时空分布，具有非线性、多尺度等突出特性[1-2]。近年来，多位学者对三峡库区蓄水后流域内降雨-径流关系进行了研究。如邬昀等[3]在三峡水库早期蓄水期对库区内径流量进行了回归分析，推求了库区各分流域未来径流量；Bosshard等[4]对三峡水库蓄水初期用半分布式水文模型PREVA对库区内水文参数进行分析，表明三峡水库在蓄水初期的度汛性能良好；Fang等[5]利用逐步多元回归方法分析了三峡大坝建成后径流变化情况，指出降雨是引起径流变化的主要原因。上述学者均针对三峡库区蓄水对水文情势的影响进行了研究，但在时间或地域上有一定的局限性，未将三峡水库各个蓄水期的水文参数进行对比研究，也未针对库区内部的水文情势进行探索。此外，三峡库区降雨-径流与水库调蓄的内在关系还存在影响因素多且分布复杂等特点，需要探索新的方法进行研究。

三峡库区万州段位于长江上游下段，地处三峡库区腹地，常年受三峡水库调蓄影响，降雨-径流关系与天然河道具有明显的差别，其内在机理对于库区内部水文情势有着重要的价值。Copula函数具有较强的捕捉随机变量间非线性关系等优点，可构建随机变量的联合分布，以诊断变量间的相关性结构变化[6]。因此，本文在构建三峡库区万州段降雨-径流联合分布的基础上，采用Copula函数诊断流域降雨-径流相关性结构的变异情况，以期为三峡库区降雨-径流等多水文要素关系变异诊断提供一条新的思路。

2 研究区域概况及数据来源

2.1 研究区域概况

三峡库区万州段位于长江中上游地区东经107°55′22″～108°53′25″、北纬30°24′00″～31°14′58″之间，属亚热带季风湿润带，气候四季分明，日照充足，雨量充沛，霜雪稀少，无霜期长。研究区年平均气温17.7 °C，年平均年日照时数1 484.4 h，年平均降水量1 243 mm，年平均蒸发总量达110×108m3。全区东西长97.25 km，南北长67.25 km，总面积为3 457 km2。境内河流纵横，均属长江水系，河流和溪涧切割深、落差大、高低悬殊，呈枝状分布。三峡水库库区主要水系图如图1所示。

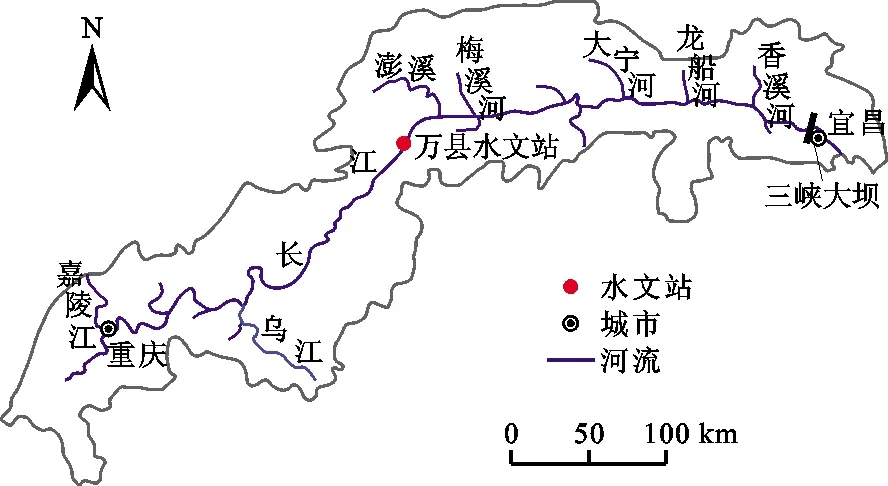
图1 三峡水库库区主要水系图

2.2 水文测点概况

万县水文站位于重庆市万州区牌楼水厂处，东经108°24′，北纬30°47′，万县水文站为长江上游下段及三峡水库库区重要的控制站，是国家基本站(流量、泥沙一类精度站)，也是库区内水文、泥沙的重要控制站和代表站，距三峡大坝约288 km，集水面积974 881 km2。万县水文站测船采用走航式ADCP常规测验方法测定年径流量，采用20cmJDZ05翻斗式自记雨量计观测降雨量。其地理位置见图1。

2.3 数据来源

收集了1977-2017年三峡水库蓄水前后41 a的降雨和径流资料。其中，最大年降雨量为1 678.5 mm，最小年降雨量为808.3 mm，多年平均降雨量为1 178 mm；最大年径流量为4 518×108m3，最小年径流量为2 573×108m3，平均年径流量3 705×108m3。将1977-2017年年降雨量和年径流量按照降序排列后得到二者的关系如图2所示。

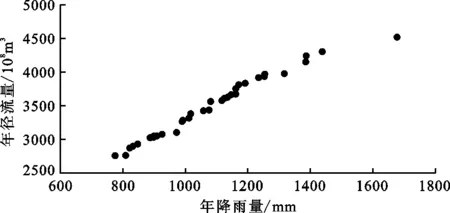
图2 1977-2017年三峡水库万州段降雨量-径流量关系

由图2可知，在三峡水库蓄水前后，库区内的降雨量-径流量关系总体呈现出一定的线性相关趋势，说明库区内降雨与径流之间仍具有水文参数的一般规律。

2.4 径流序列平稳性检测

考虑到水文序列自相关性对检测结果的影响，采取TFPW算法对各时段的实测降雨量和径流量进行序列相关性检验，即代入Pettitt-BS耦合模型进行编译检验[7-8]。经检验，三峡库区径流序列潜在变异点分别为2003、2007和2013年，与三峡水库施工蓄水、初期蓄水和试验性蓄水的时间相吻合。

为了验证变异点的检验效果，对不同时段的径流序列统计参数进行对比分析，如表1所示。由表1可见，总体而言，2007年前后的径流量均值有一定差异，标准差、方差、偏态系数变化不大，一阶偏自相关系数差异较大，尤其是水库蓄水前后差异较为明显。所以，库区内部水文序列特性与天然河道相比存在变异性，三峡水库蓄水过程对二者关系有一定的影响，需要进一步评估。

表1 1977-2017年不同时段研究区径流序列统计参数对比

3 降雨-径流Copula函数的建立

3.1 边缘分布函数

由于Copula函数模型不受边缘分布型式的限制，可以择优采用边缘分布[9]，对年降雨量、年径流量在1977-2002(阶段1)，2003-2012(阶段2)，2013-2017(阶段3)3个阶段的边缘分布分别采用皮尔逊Ⅲ型分布(P-Ⅲ)[10]、对数正态分布(logarithmic normal distribution, log n)[10]和Gumbel分布[12]进行经验频率拟合计算，其计算式分别如下。

皮尔逊Ⅲ型分布函数：

(1)

(2)

(3)

(4)

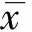
对数正态分布函数：

(5)

(x≥0)

式中：P为X≤x的拟合理论概率；u=Ex为样本的对数均值；δ为样本的对数均方差。

Gumbel分布函数：

(6)

(7)

μ=K-rη

(8)

式中：P为X≤x的拟合理论概率；μ为位置参数；η为尺度参数；S为样本的均值；K为样本的均方差；r为欧拉常数。

采用矩估计法对上述不同边缘分布模型进行参数估计，分别计算出降雨量和径流量对应公式(1)～(8)中的关键参数，结果见表2。

由表2确定出1977-2017年不同阶段各边缘分布函数，进而绘制万县水文站年降雨量和年径流量的各边缘分布曲线。同时将各实测的数据与边缘分布曲线进行对比，如图3所示。

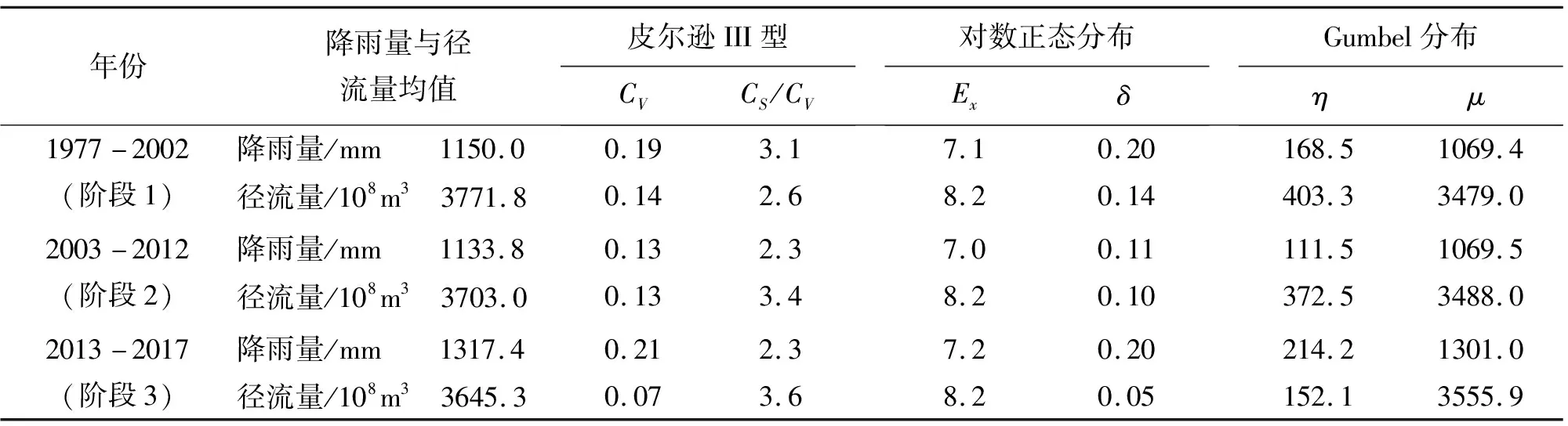
表2 1977-2017年不同阶段各边缘分布函数降雨量和径流量对应参数的估计结果

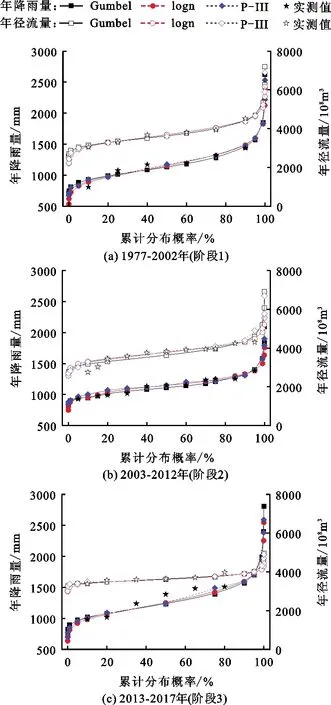
图3 1977-2017年不同阶段万县水文站年降雨量和年径流量的边缘分布曲线

由图3可知，不同阶段年降雨量和年径流量的边缘分布曲线呈现出不同的趋势，但3种边缘分布曲线与实际数据均能较好地拟合。

将上述3种边缘分布函数拟合的经验频率与实际经验频率进行误差分析，通过评价指标选择拟合效果最好的(即误差最小)的缘分布函数进行联合分布计算。

3.2 评价指标

分别计算出各边缘分布对应的均方根误差(root mean squared error,RMSE)和赤池信息准则(Akaike information criterion，AIC)指标，模型的检验结果见表3。由表3可知，依据指标值最小准则，降雨分布模型拟合优度评价指标在阶段1的最小值分别为78.2和80.7(RSME和AIC，下同)，阶段2最小值分别为34.6和70.0，阶段3最小值分别为112.3和134.4；径流分布模型拟合优度评价指标在阶段1的最小值分别为193.9和202.4，阶段2最小值分别为132.3和193.2，阶段3最小值分别为80.5和90.3。进而遴选出不同阶段降雨量和径流量的最佳的边缘分布函数进行联合分布计算。

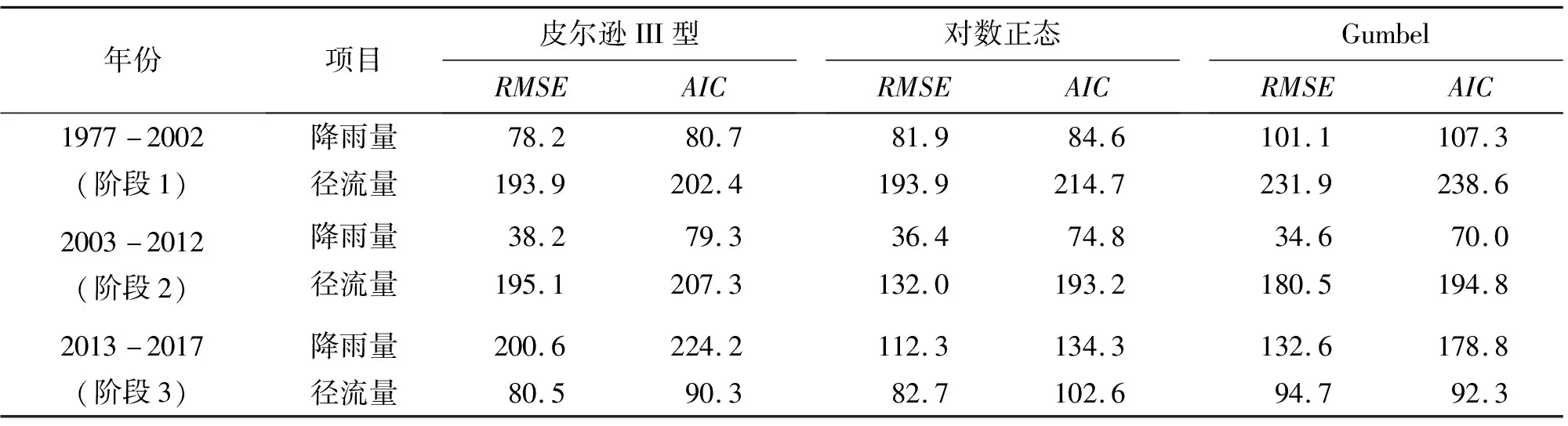
表3 1977-2017年不同阶段万县水文站降雨量和径流量分布模型拟合优度检验结果

3.3 Copula联合分布的建立

选用Clayton Copula和Gumbel-Hougaard Copula两种构造函数来建立联合分布函数[13]，结合Copula函数模型对其进行计算，以得到降雨-径流的联合分布函数。不同阶段两种Copula联合分布函数参数θ的计算结果如表4所示。

由表4可见，库区蓄水前后的降雨-径流联合分布有所改变，θ值也需采用RMSE与AIC指标进行检验，即选取较小的指标值来确定出不同阶段最佳的联合分布函数[14]。具体如下：

表4 不同阶段两种Copula联合分布函数参数θ值

1977-2002年(阶段1)，θ最佳值为3.24，降雨-径流联合分布服从Clayton Copula分布：

φ(x,y)=(u1-3.24+u2-3.24-1)1/-3.24

(9)

2003-2012年(阶段2)，θ最佳值为2.73，降雨-径流联合分布服从Gumbel-Hougaard Copula分布：

(10)

2013-2017年(阶段3)，θ最佳值为2.02，降雨-径流联合分布服从Gumbel-Hougaard Copula分布：

(11)

公式(9)、(10)和(11)即为三峡库区万州段在各蓄水阶段的Copula联合分布，联合分布函数模型至此已经建立完毕，后文将基于上述公式和参数进行分析。

4 三峡水库蓄水过程对万州段降雨量和径流量的影响

4.1 边缘分布的改变

在三峡水库的蓄水过程中，库区内部万州段的降雨量和径流量的边缘分布均发生了较大的改变。

阶段1：该阶段长江万州段属于天然河道，根据表3中降雨量和径流量分布模型拟合优度的检验结果，未蓄水时长江中上游的降雨量和径流量的边缘分布均采用皮尔逊III型分布最为合理，其CV值分别为0.19和0.14，对应的CS/CV分别为3.1和2.6(表2)，符合我国水利行业规范所推荐的河道水文参数的频率曲线，说明此时降雨量和径流量边缘分布满足一般天然河道的特点。

阶段2：三峡水库处于相对低水位蓄水运行(蓄水位为135～156 m)，库水位变动较大。根据表3，降雨量边缘分布采用Gumbel分布最为合理，其尺度参数η=111.5，位置参数μ=1 069.5(表2)；径流量边缘分布最合理的是对数正态分布，其样本对数均值Ex=8.2，对数均方差δ=0.1(表2)。这说明在施工期蓄水和初期蓄水阶段，三峡水库万州段已经不同于天然河道，其降雨和径流分布开始受到影响。

阶段3：随着库水位175 m试验性蓄水的进行，径流量在水库的调蓄下趋于稳定，降雨量呈现出新的分布情况。根据表3，此时降雨量的边缘分布采用对数正态分布最合理，其样本对数均值Ex=7.2，样本均方差δ=0.2(表2)；而径流量恢复至皮尔逊III型分布，但参数有所改变，此时CV=0.07，CS/CV=3.6。

4.2 联合分布的改变

根据3.3节降雨量-径流量联合分布函数的模拟计算结果，绘制1977-2017年不同阶段三峡库区万州段降雨量-径流量联合分布图及等值线图，如图4所示。

由图4并结合Copula的函数特性可知，联合分布在单一平面上的投影是该平面对应的边缘分布函数，等值线图中的拐点为联合分布的精确值。图4中用虚线连接各联合分布概率等值线的拐点值，并称这一虚线为联合概率分布趋势线。此外，对比图4各阶段联合分布图和分布概率等值线图不难发现，等值线的疏密反映了降雨量和径流量年际波动的大小，等值线越稀疏，说明该参数年际波动越大；反之，则说明参数的波动和变化较小，联合概率分布趋势线会偏向波动较小的参数等值线[15]。为了定量分析库区内蓄水前后水文参数的变化，将分布概率为0.2的等值线对应的值视为小概率值，其反映了某阶段较难发生的水文情况；将分布概率为0.8的等值线对应的值视为大概率值；将分布概率为0.2～0.8的等值线范围称为分布区间，反映了某阶段水文变化程度。基于此，分析各阶段变化规律如下：

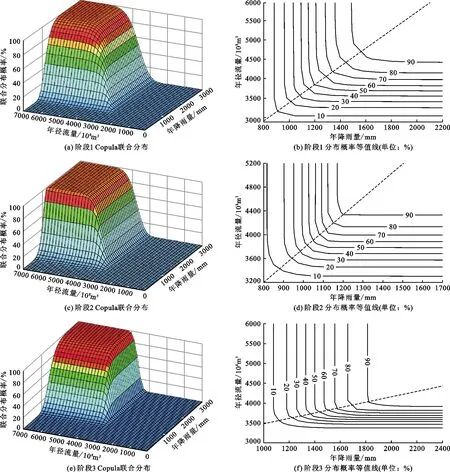
图4 1977-2017年不同阶段研究区降雨量-径流量Copula联合分布模拟结果

阶段1，降雨量和径流量年际变化和波动均较大，联合概率分布趋势线基本位于分布概率等值线图的对角线位置，符合天然河道水文参数变化规律。研究区域年降雨量均值为1 150 mm，Copula模拟年降雨量对应的小概率值和大概率值分别为971.1和1 358.2 mm。年径流量的小概率值和大概率值分别为3 263.7×108和4 129.0×108m3。

阶段2，径流量受三峡水库蓄水水位波动(蓄水位在135～156 m之间波动)的影响，年径流量年际变化较大，而期间降雨并未受到较大影响。联合概率分布趋势线偏向降雨量等值线，斜率相对阶段1变大。年降雨量均值为1 133.8 mm，年均降雨量较阶段1减少1.4%，变化幅度较小。年降雨量对应的小概率值和大概率值分别为901.3和1 139.5 mm，较阶段1的年降雨量小概率值和大概率值均有减少，其减幅分别为7.2%和16.1%，其降雨量联合分布区间变幅减小了38.4%，减幅明显。年径流量对应的小概率值和大概率值分别为3 453.5×108和4 140.5×108m3，较阶段1年径流量的小概率值和大概率值分别增加5.8%和0.3%，年径流量分布区间由865.3×108m3减小至687×108m3，减小了20.6%，减幅明显。

阶段3，三峡水库试验性蓄水后并出现常态化(蓄水位175 m)，受水库调蓄作用的影响，年径流量处于相对稳定状态，年际变化较小，而年降雨量等值线间距大，年际变化也较大，降雨量处于整体增大的状态。此时，联合概率分布趋势线明显偏向径流量等值线，斜率变小。年降雨量均值为1 317.4 mm，较阶段1年降雨量均值增大14.6%，增幅明显，对应的小概率值和大概率值分别为1 178.8和1 660.5 mm，较阶段1均有增大，增幅大约20%，年降雨量分布区间变幅增加了24.5%。年径流量对应的小概率值和大概率值分别为3 466.8×108和3 838.5×108m3，与其他两个阶段相比，其小概率值均增加而大概率值均减小，与阶段1相比，小概率值增幅为6.2%；大概率值减幅为7.0%，变幅区间371.7×108m3，减少57%。

4.3 边缘—联合分布趋势分析

为了更好地分析三峡水库蓄水前后研究区降雨-径流关系和预测未来水文变化趋势，将边缘分布和联合分布进行整合分析，所得趋势线分布图如图5所示。根据图5，拟合出不同阶段年径流量和年降雨量边缘—联合分布趋势线的线性表达式，如表5所示。

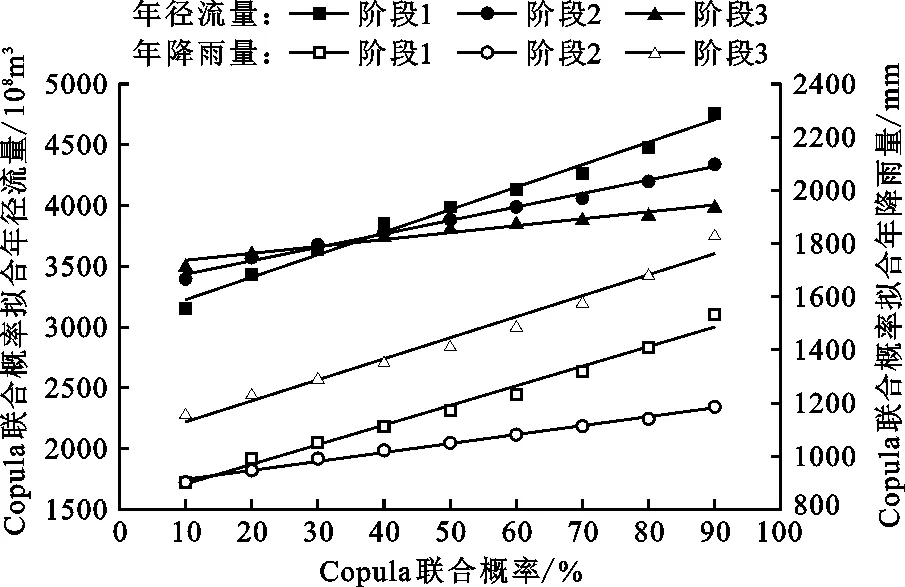
图5 1977-2017年不同阶段研究区降雨量和径流量边缘—联合分布趋势

表5 1977-2017年不同阶段研究区年径流量和年降雨量边缘—联合分布趋势线的线性表达式

由表5中各拟合式的R2值可知，各拟合线的误差均较小，可以作为预测的数据支撑，将各阶段具体分析如下：

阶段1，年降雨量和年径流量的线性趋势基本一致。阶段2，两线有一定的发散趋势，其中年径流量的拟合线斜率比阶段1减小747，减幅为40.3%，初始值则增加284，增幅为9.3%。阶段3的年径流量趋势线斜率较阶段1、2明显减小，变化趋缓，表明在三峡水库的调控下，年径流量已趋于稳定；阶段3的年降雨量分布也同样变化明显，起始值比阶段1增大27.8%，但斜率仅增大7.1%，表明研究区在三峡水库蓄水完毕后降雨总量增大，但与自然阶段相近。

4.4 研究区未来降雨量-径流量变化预测

三峡库区万州段的年降雨量-径流量受水库调蓄等因素影响，将处于一个比较稳定的分布区间，2013年水库试验性蓄水以后，根据年径流量线性拟合式y=571x+3 490可推测未来径流分布，三峡库区万州段最小年径流量大致为3 490×108m3(±5%)，最大年径流量约为4 055×108m3(±5%)。同理根据年降雨量的线性拟合公式y=792.5x+1 048，可知该区域最小年降雨量为1 048 mm(±5%)，最大值不超过1 842 mm(±5%)。

此外，根据上述关系还可以推断出不同保证率情况下，对应的降雨量和径流量。

5 讨 论

5.1 降雨量变化的讨论

阶段3降雨量较阶段1、2均有所增加，且维持相对稳定的波动区间。降雨是水文循环的重要环节，降雨量主要受海陆位置、地形地貌等宏观层面因素的影响，王文鹏等[1]研究发现三峡水库蓄水后，上游流域短历时降水集中出现的次数增加，降水强度增大，该类降水量占总降水量的比例较大，而长历时降水出现频次降低[16]。

长江流域与其他地区许多河流相比，整个流域的降雨量非常大，尤其在长江中上游地区，而年际变化很小。三峡水库蓄水至175 m后，流域库区水体表面积扩大了3～4倍[17]，从而产生丰富的水汽，在山区特殊的地形地貌下，促使水汽上升，加大了降水概率。当然，作为水文循环的一部分，区域降雨量的主要影响因素还是宏观层面的，上述分析只是研究区在阶段3降雨量增加的可能原因。

5.2 径流量减小的原因

三峡水库蓄水后，万州段水文关系出现变化还可能与以下因素有关。

(1)上游水库大坝的修建：除了宏观水文循环因素，导致径流量减小的主要原因还是人为作用。自2003年三峡水库蓄水以来，水库上游修建了大量的梯级电站和用于灌溉、调水等的水库[18]。根据国际大坝委员会(International Commission on Large Dams, ICOLD)数据集[19]，长江流域有22 185座水坝，总库容量为2 320×108m3，约占长江年径流量的26.0%；其中，位于万州上游的大坝数量约占总数的74.3%。在所有水坝中有840座为灌溉型水坝，另有762座水坝以灌溉为主要目的，两者总库容为55×108m3，占长江年径流量的0.6%。

(2)水土保持：导致径流减少的另一个因素为上游植被覆盖率的变化。自三峡水库蓄水后，近十多年来国家在水土保持和植被恢复方面投入力度越来越大[20]，长江上游植被覆盖率明显增大。植被覆盖的增大使沿江地区的水土保持能力更好，降雨水量更多地被滞留在了陆地上。

(3)城镇化建设和人口发展：万州及其上游长江流域城镇化建设发展迅猛，人口急剧增加，从而导致对水的需求量增大。但也有研究表明，在城镇化较高地区，这些增加的生活用水量部分又以废水形式最终返回河流，因而对流域径流量的影响有限[21]。因此，关于该部分的影响评估仍需要开展大量的研究工作。此外，影响长江上游径流量的因素还有很多，如跨流域调水等。

6 结 论

(1)Copula模型能较好诊断三峡库区特定河段的水文关系，这为库区河道多水文要素关系变异诊断提供了新思路。

(2)三峡水库万州段在天然河道阶段，降雨量和径流量均采用皮尔逊III型分布最为合理，其Copula联合分布采用θ=3.24的Clayton Copula分布较好；施工期和初步蓄水阶段，降雨量分布变为Gumbel分布，径流变为对数正态分布，其联合分布变为θ=2.73的Gumbel-Hougaard Copula分布；试验性蓄水阶段，降雨量分布变为对数正态分布，径流量恢复至皮尔逊III型分布，其联合分布变为θ=2.02的Gumbel-Hougaard Copula分布。

(3)施工期及初步蓄水阶段较天然河道阶段的降雨量联合分布区间变幅减小38.4%；年径流量变幅区间减少20.6%。试验性蓄水阶段的年降雨量较天然河道增大，变幅区间增加24.5%，年径流量变幅区间减少57%，变化梯度趋缓。

(4)预测三峡库区万州段未来年径流量应不小于3 490×108m3(±5%)，最大年径流量不超过4 055×108m3(±5%)；年降雨量不小于1 048 mm(±5%)，最大年降雨量不超过1 842mm(±5%)。