多类地球重力场模型的高程异常精度比较

何亚军，陈晓茜

（1.中铁第四勘察设计院集团有限公司，湖北 武汉 430063；2.湖北省基础地理信息中心（湖北省北斗卫星导航应用技术研究院），湖北 武汉 430074）

地球重力场反映了地球内部的物质分布和地球旋转运动信息，作为基本的地学信息，其在地球物理学、现代大地测量学、地球动力学等学科研究中有着重要的作用。大地测量中的地球重力场主要以截断到一定阶次的球谐位系数来表示，称为地球重力场模型。当前高精度高分辨率地球重力场模型的确定在国际上广受重视，已有多个国家发射专门用于重力探测的重力卫星进行地球重力场测量，如德国的CHAMP卫星、美德的GRACE卫星、欧洲的GOCE卫星以及美德的GRACE-FO卫星等，我国重力卫星也在筹备阶段。重力卫星主要采用卫星地面跟踪技术、卫星跟踪卫星技术以及卫星重力梯度技术测定地球重力场，并结合地面重力、航空重力观测资料和卫星测高资料反演出较高精度的地球重力场模型[1-3]。

目前，国际地球模型中心ICGEM已收录静态地球重力场模型176个，这些重力场模型在大地测量和工程测量方面有着广泛应用，比如利用地球重力场模型可计算GNSS点高程异常，从而将GNSS大地高转换为工程测量所需的正常高，减少水准测量的工作；其次利用地球重力场模型可计算水准测量中的正常水准面不平行改正和重力异常改正，提高水准测量精度，满足海拔变化剧烈地区的水准测量需求[4]。本文利用中国某区域的GNSS点数据，利用多个地球重力场模型计算各点高程异常，并与各点实测高程异常相比较，检验多类地球重力场模型的精度，为工程测量实践工作提供参考和借鉴。

1 原理与方法

1.1 地球重力场模型高程异常计算

地球重力场的引力位是一个逼近地球质体外部引力位在无穷远处收敛到零值的调和函数，通常展开为一个在理论上收敛的整阶次球谐或椭球谐函数的无穷级数，这个级数展开系数的集合定义一个相应的地球重力场模型。利用地球重力场模型根据扰动位原理计算高程异常可表示为[5-7]

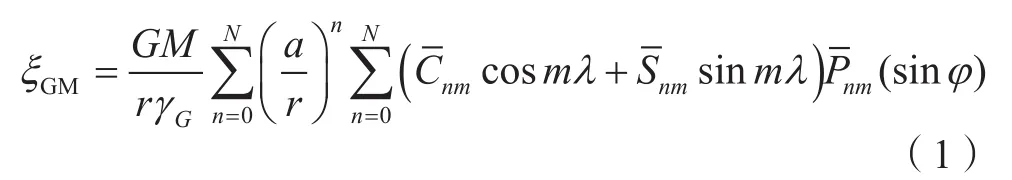
式中，GM为地球引力常数；r为地心向径；a为参考椭球长半轴（a=6 378 137.0 m，采用CGCS2000参考椭球，以下椭球参数均相同）；和为减去正常椭球重力场后的完全规格化球谐位系数；(sinφ)为完全规格化缔合勒让德函数（可采用跨阶次递推法）；φ为地心纬度；λ为地心经度；γG为GNSS点处的正常重力。

在确定赤道处的正常重力γEQ后，根据熟知的Somigliana公式，即可计算椭球表面大地纬度为B处的正常重力γSF，可表示为[8]

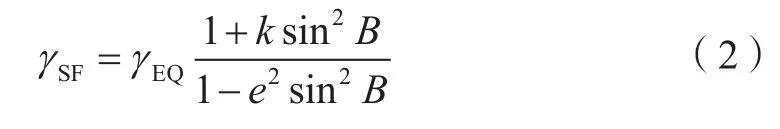
式中，K为理论正常重力公式常数（K=0.101 931 852 619 31）；e为参考椭球第一偏心率（e=0.081 819 191 042 816）；γEQ代表赤道处正常重力。

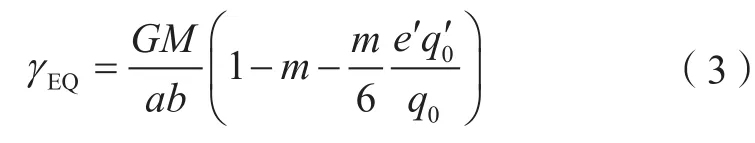
式中，e′为第二偏心率（e′=0.082 094 438 151 917）。q0、q′0、m的计算公式分别为

式中，x、y、z代表计算点的地固直角坐标；u为椭球坐标中的共焦椭球短半轴；b为参考椭球短半轴（b=6 353 752.314 1 m）；E=（a2-b2）为线偏心率；ω为参考椭球角速度。

GNSS点处正常重力γG计算公式为：

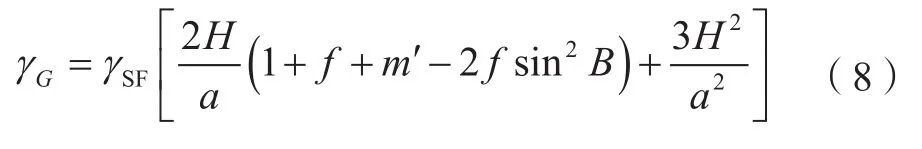
式中，H为GNSS点的大地高；f为参考椭球扁率。m′的计算公式为：

1.2 GNSS点实测高程异常计算

高程异常是似大地水准面与参考椭球面之间的高差。目前GNSS测量技术可以测定高精度的大地高，水准或三角高程测量精确测定点位正常高，即可计算该点的实测高程异常。GNSS实测点高程异常可表示为：

式中，H为该点的大地高；h为该点的正常高。

GNSS测定的大地高及水准测量的正常高已能达到毫米级精度，计算的高程异常即可达到较高精度。而直接利用国际地球重力场模型解算GNSS点高程异常并未能达到如此高的精度，首先其所基于的椭球面或似大地水准面与我国高程系统存在一定的系统偏差，且重力场模型在计算中需截断至一定阶次，本身也存在一定误差。因此，为了提高重力场模型解算高程异常的精度，应加入系统偏差加以改善，系统偏差计算采用分区常系统偏差矫正法和直接计算法，计算公式分别为式（11）和式（12）。

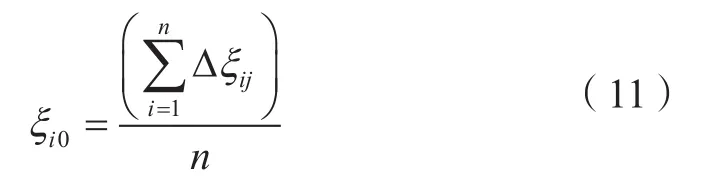
式中，ξi0为i分区中的计算的常系统偏差值；ξij为i分区中的第j个实测高程异常值与模型值的差值；n为i分区中的GNSS点数。

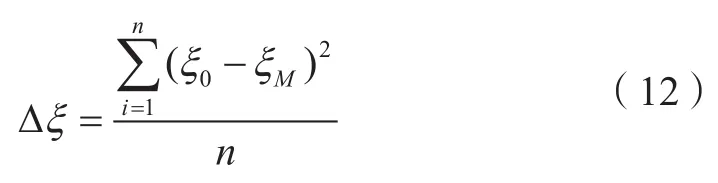
式中，ξ0为GNSS点实测高程异常；ξM为GNSS点重力场模型高程异常；i为点号，n为GNSS点的总数目。

1.3 精度评定标准

采用相关系数（r）、均方根误差（RMSE）、纳什系数（NSE）作为评定标准，对模型高程异常和实测高程异常差值的精度和两者的相关性以及重力场模型的解算质量进行检验。相关系数用于检验两者的相关程度；均方根误差确定未加入系统偏差和加入系统偏差的高程异常差值精度，检验系统偏差对结果精度的改善效果；纳什系数检验重力场模型解算高程异常值的整体质量，具体计算公式为：

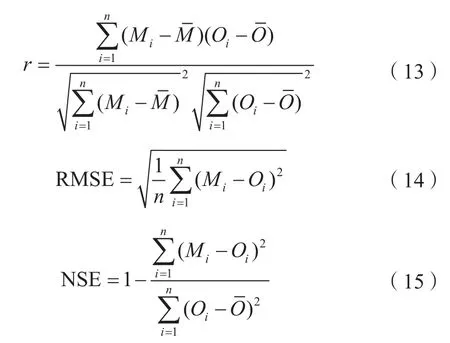
式中，Mi为模型高程异常值；Oi为实测高程异常值；和分别代表所有GNSS点模型高程异常和实测高程异常的平均值。

2 实例分析

选择安徽省至江苏省某铁路安徽段的GNSS点数据作为研究资料，共有70个GNSS/水准点，均采用CGCS2000国家大地坐标系参考椭球体，高程系统采用1985国家高程系统，如图1所示。

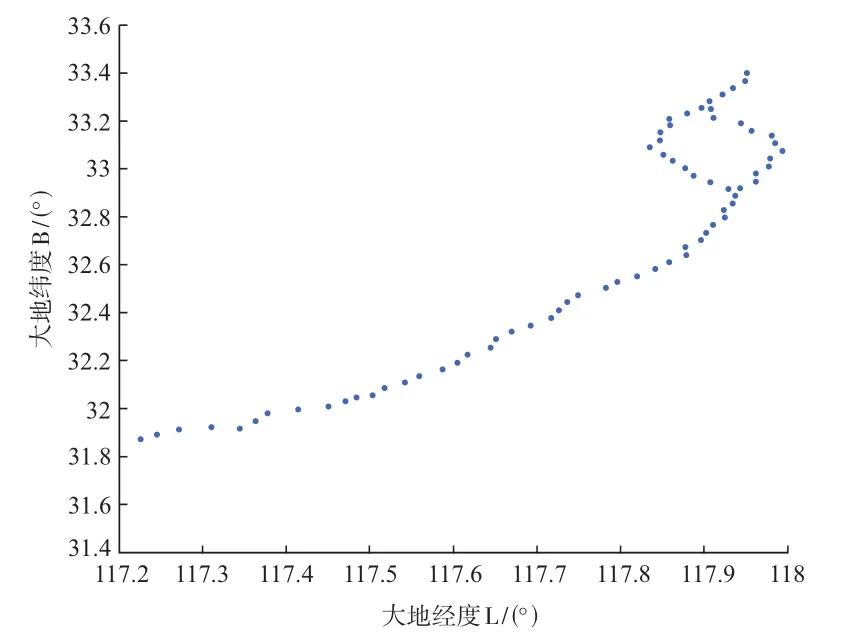
图1 GNSS/水准点线路分布

选取了10个精度较好的地球重力场模型进行模型高程异常的计算，各个模型的公布年份、数据来源、研制者以及最高阶数见表1。

表1 地球重力场模型对比

根据图1显示，GNSS/水准点经纬度变化范围较小，且呈现规律性，故采用分区常系统偏差矫正法时，将其按照一个区域进行分区进行系统偏差，具体精度结果见表2。采用分区常系统偏差矫正法消除系统误差后，GECO模型解算精度最高，高达3.94 cm，相比较未降低系统偏差的结果精度提高了81.32%。整体上看，各个模型的高程异常精度提高显著，系统偏差改善效果明显。

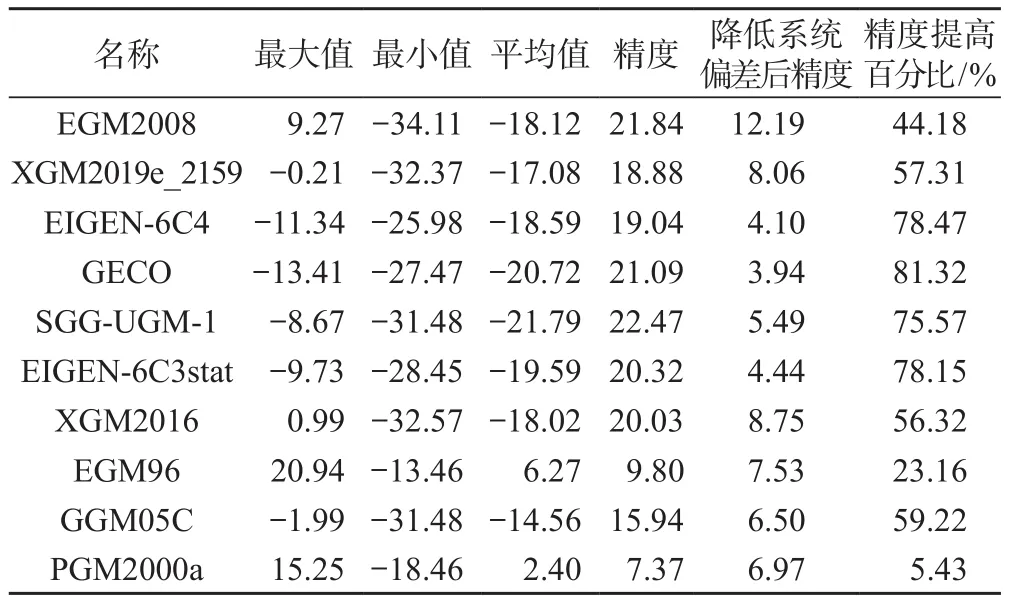
表2 分区常系统偏差矫正法降低系统偏差精度统计结果/cm

表3给出了各模型采用直接计算法解算的高程异常值与GNSS/水准点实测高程异常的比较结果，在降低系统偏差后，XGM2019e_2159、EGM2008、EIGEN-6C4、GECO、SGG-UGM-1、EIGEN-6C3stat 6个高阶重力场模型中，EIGEN-6C4模型解算精度最高，为15.52 cm；XGM2016、EGM96、GGM05C、PGM2000a4个低阶重力场模型中，PGM2000a模型解算精度最高，高达7.22 cm。同时整体上，在降低系统偏差后，各个模型的高程异常精度均有所提高，其中高阶重力场模型提高幅度相较低阶重力场模型更为显著，提升范围为16%～21%。但直接计算法降低系统偏差后的精度结果相比较分区常系统偏差矫正法的精度结果，解算精度数值低，系统误差并没有完全消除，仍然需要改善。

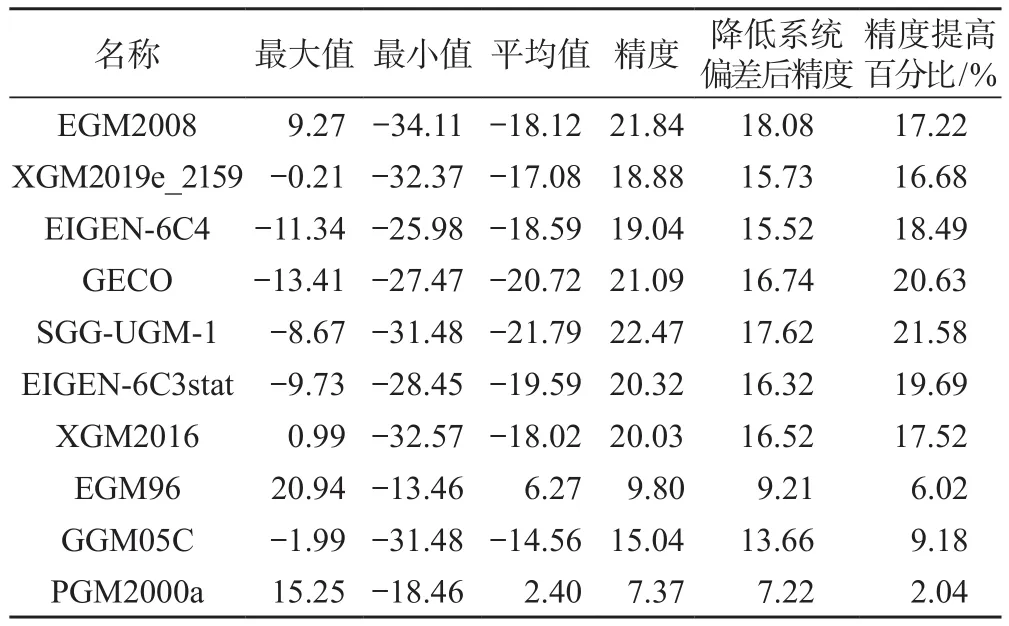
表3 直接计算法降低系统偏差精度统计结果/cm

对比两种系统偏差计算法的精度结果，分区常系统偏差矫正法的精度提升效果更为明显，模型解算值更为接近真实高程异常值。

利用相关系数（r）、纳什系数（NSE）可计算出各个模型的精度比较结果，检验模型高程异常与实测高程异常的符合程度，具体计算结果见图2、3。图2、3结果表明采用两种降低系统偏差方法下，各个模型的相关系数均在0.95以上，说明模型高程异常与实测高程异常具有高度相关关系。此外，各个模型的纳什系数均在0.8以上，说明重力场模型解算结果可信度高，模型质量好。对比图2、3，可比较出两种降低系统偏差方法计算出的各模型结果的相关系数极为接近，而纳什系数在数值上，分区常系统偏差矫正法明显优于直接计算法，更适合于重力场模型解算高精度高程异常。

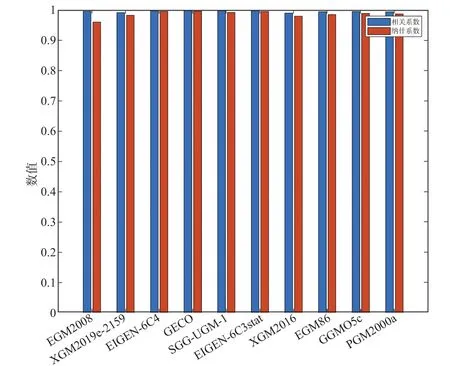
图2 分区常系统偏差矫正法精度评定结果图

考虑到实际工作中GNSS/水准点的数据存在不完整情况，故选择单个点位模型高程异常值与实测高程异常值的差值直接作为系统偏差改善模型解算精度，考察该种方法的解算精度，检验其是否用于今后的工程实践中。由于分区常系统偏差矫正法降低系统偏差效果更好，故选择该方法的RMSE精度值作为参考值，限定精度差值为3 cm进行计算，确定满足条件的GNSS/水准点数目，检验总点位的符合情况，具体计算结果如表4。据表4结果可知，整体上各个模型计算的符合条件的点位数比较理想，最低个数为32，最高个数为57，解算精度效果较为理想。在点位实测数据缺失的情况下，可选择合适点位模型值与实测高程异常值的差值作为系统偏差，提高模型解算精度，减少测量工作任务量。特别在项目初步设计即草测或初测阶段，甚至在定测阶段，线路方案不稳定，比较方案较多，在只进行优选方案的水准测量及所有方案的GNSS测量情况下，选取分区常系统偏差矫正法精度最优且该模型下计算的符合条件的点位数较多的地球重力场模型，即可计算出满足精度要求的比较方案的GNSS点的正常高，大大减少了水准测量工作量。或在项目初步设计阶段，收集线路沿线一定数量有正常高及CGCS2000国家大地测量成果，在只测量框架网（CP0）及基础平面控制网（CPI）的情况下，选取分区常系统偏差矫正法精度最优的地球重力场模型，计算所有GNSS点的正常高，大大缩减了勘测前期精测网准备阶段工期及省去了繁重的水准测量工作。

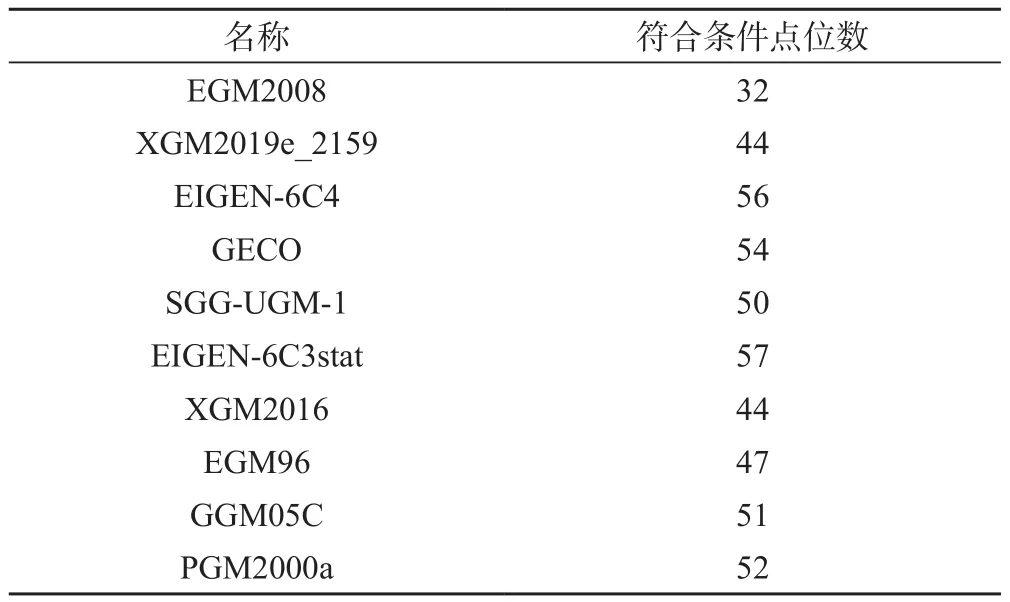
表4 各种模型计算符合条件点位数统计结果/个

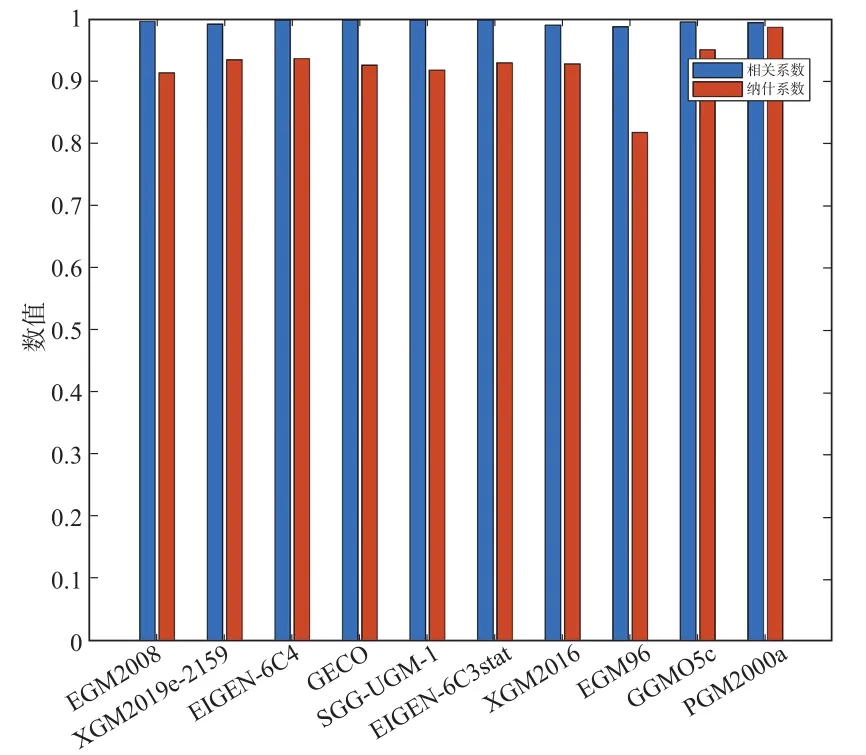
图3 直接计算法精度评定结果图

3 结 语

根据各个模型解算的该铁路GNSS点的高程异常结果可得，各个重力场模型计算的相关系数、均方根误差以及纳什系数三项精度评定值均符合限值范围，其中GECO模型高程异常解算值降低系统偏差后精度值高达3.94 cm，相关系数和纳什系数也极为理想，最为符合实测高程异常。利用地球重力场模型解算GNSS点高程异常相比较传统的人力测量有着快速、简便、工作量小等诸多优势，可大大缩减测量工期及节省测量所需的人力、物力资源。伴随着我国未来也将发射重力卫星，将可得到精度和分辨率更高的地球重力场模型，同时利用多个重力场模型进行组合计算，可进一步提高高程异常的精度，未来单独使用地球重力场模型解算高程异常的精度将有望达到四等或三等水准测量，在工程测量方面发挥出更加重要的作用。