超材料完美吸波器的等效电路模型研究
陆浩然 ,郭云胜
(1.中国核科技信息与经济研究院,北京 100084;2.内蒙古科技大学 理学院,内蒙古 包头 014010)
超材料吸波器具有吸收强、质量轻、厚度薄、频率可调等优点,在隐身、安全防护、抗干扰等方面具有广泛的应用[1-3]。超材料完美吸波器[4]自2008 年被首次报道以来,围绕它的研究工作主要包括:工作波长从微波逐渐向太赫兹、红外和可见光波段提升,工作方式逐渐从单频向双频、多频及宽频带转化,工作频率从固定型向可调型方面拓展,工作状态从极化敏感型向极化不敏感型方向转变。由此看出,为满足不同要求,超材料单元结构也应具有不同的形式。迄今为止,研制出的完美吸波超材料的单元结构非常多,如同时含有金属电谐振器和磁谐振器结构[4]、金属底板及其上面的金属图案谐振器结构[5-6]、金属底板及其上面的介质谐振器结构[7-8]和全介质型惠更斯超表面结构[9-10]等。对于不同的单元结构形式,电磁波与它们相互作用的方式也不一样,导致吸波机理有所不同。但是,无论何种结构形式,谐振吸收是所有超材料吸波的共同属性。本文以是否含有金属底板为分界线,把所有超材料吸波器的单元结构分为两类,分别用含有LC 谐振和电阻R 的一端口网络和二端口网络表示出来,分析不同单元结构的吸波机理并比较它们的异同。
1 二端口网络的全反射和全透射
一般而言,波的吸收同时伴随着波的反射和透射,是一个典型的二端口网络问题。二端口网络中,反射系数用S11表示,透射系数用S21表示,由此决定的反射率为透射率为吸收率为超材料的吸波性能完全可以用二端口等效电路的方式进行描述和分析[11-12]。在提取超材料完美吸波的等效电路之前,先对二端口网络的全反射和全透射做一简单的分析和说明。由于与超材料吸收相关的入射波、反射波和透射波一般都是在空气中传播的,所以在等效电路模型中,分别用377 Ω 的源电阻RS和负载电阻RL表示吸波超材料两侧空气的阻抗,如图1 所示。电磁波与超材料相互作用导致反射波和透射波的振幅和相位等物理量的改变完全可以用电路中的电感、电容和电阻等元件进行描述,本文把这些表示在二端口网络的虚线框内。如果把二端口网络直接导通或短路,就可得到入射波的全透射和全反射,其等效电路分别如图1(a)和1(b)所示。
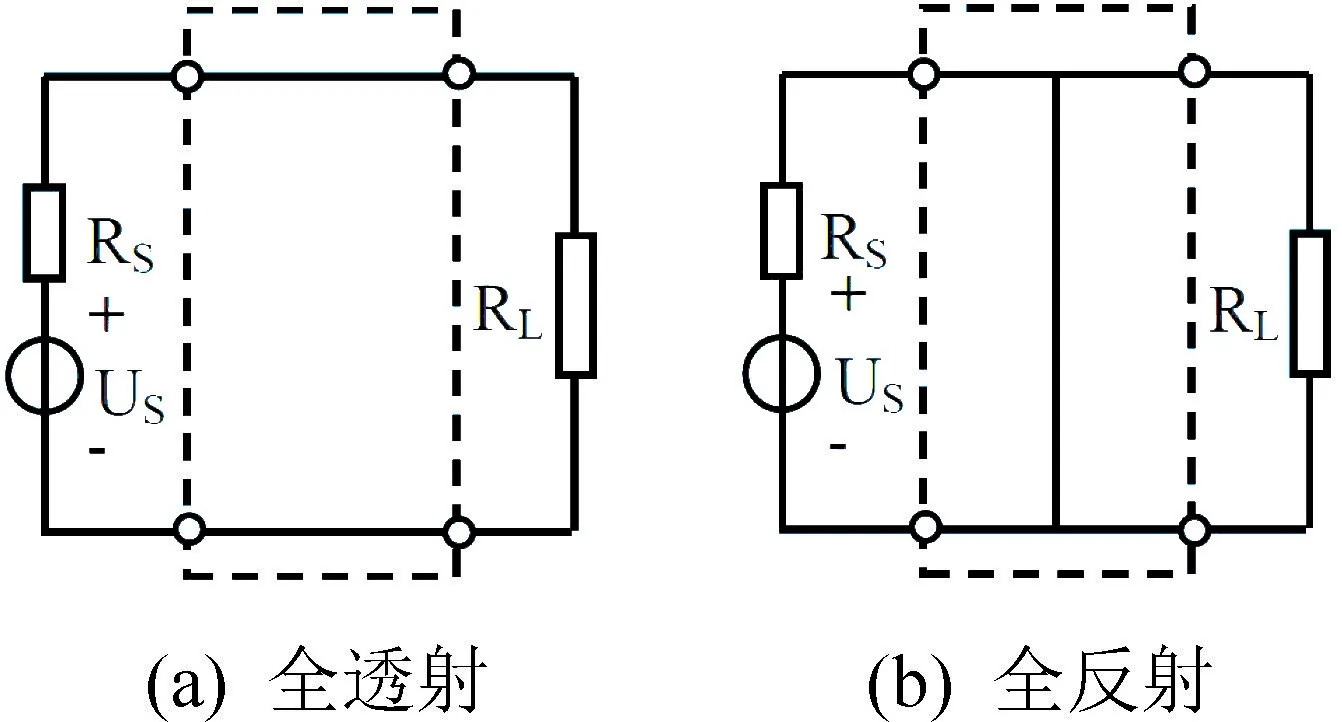
图1 二端口网络等效电路Fig.1 Two-port network equivalent circuit
2 超材料全反射的二端口网络等效电路
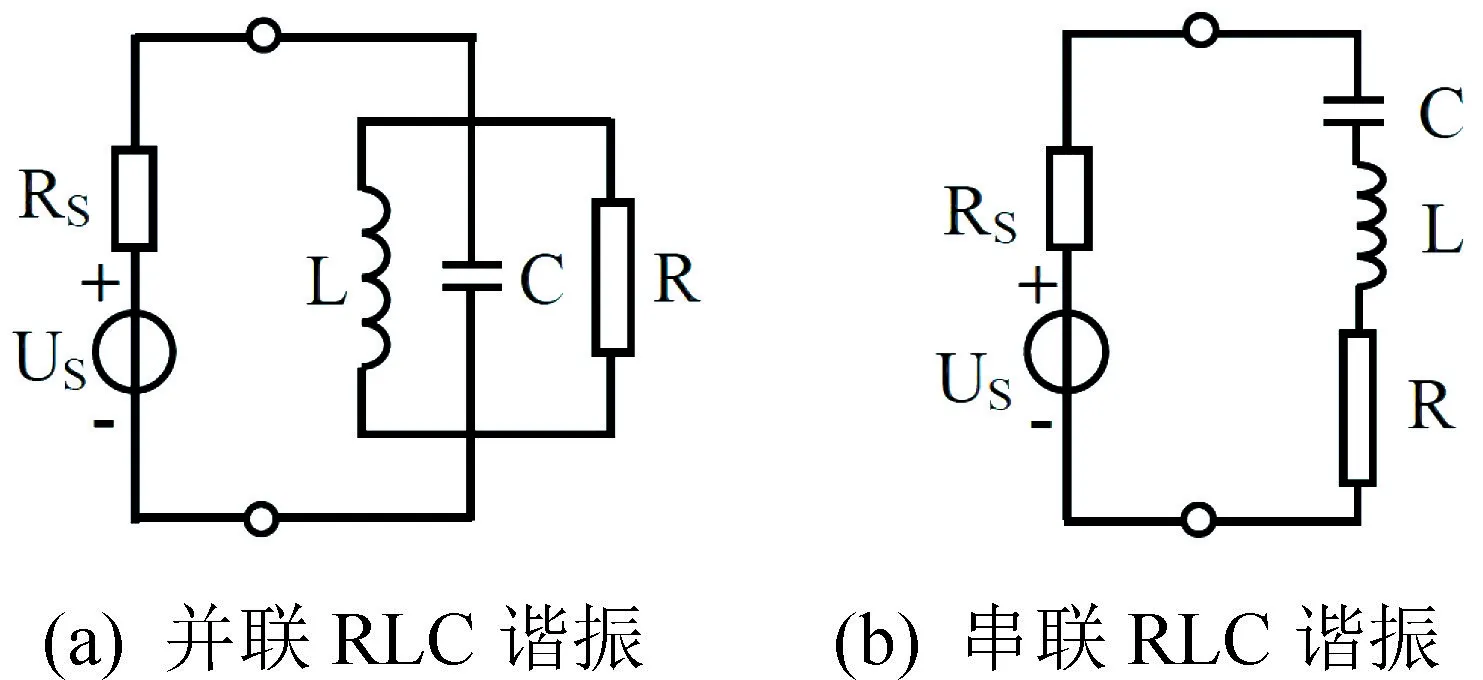
超材料的超常特性是由人工原子(亚波长电磁谐振结构)的谐振引起的[13-15],完美吸收效应也不例外。所以,应该在二端口网络中加入LC 谐振电路表示超材料的谐振行为。电偶极子谐振和磁偶极子谐振是超材料的两种基本谐振模态,它们在超材料的构造中起着非常重要的作用。理想金属或介质材料构成的电偶极子或磁偶极子谐振都能使入射的电磁波完全反射,全反射的等效电路如图2 所示,其中图2(a)为在串联支路中加入并联LC 谐振电路的形式,图2(b)为在并联支路中加入串联LC 谐振电路的形式。电路的谐振频率由L和C共同确定,带宽由Q值决定。
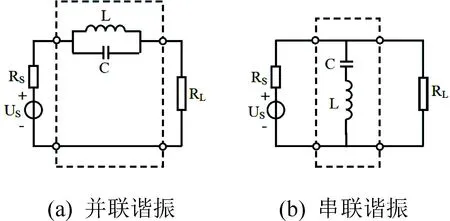
图2 超材料全反射等效电路Fig.2 Total reflection equivalent circuit of metamaterials
采用电路仿真软件ADS 模拟谐振频率为10 GHz 时并联谐振和串联谐振中不同Q值对应的带宽,分别如图3 和图4 所示。从图3(a)~(c)仿真结果可知,对于图2(a)中的并联谐振形式,在保持电感和电容乘积一定的情况下,Q值越大,带宽越窄;从图4(a)~(c)仿真结果可知,对于图2(b)中的串联谐振形式,带宽随Q值的变化与并联谐振完全相同。这里谐振带宽随Q值的变化对超材料完美吸收的带宽具有重要的指导作用。
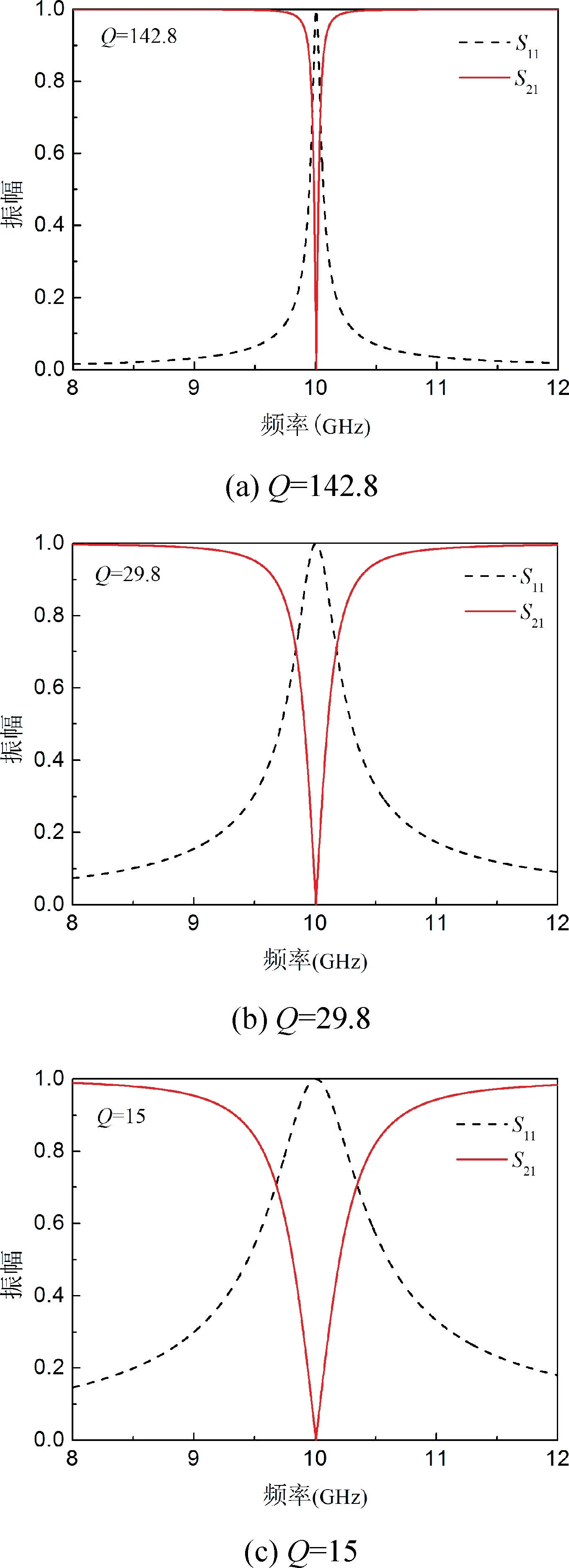
图3 并联谐振中的Q 值对带宽的影响Fig.3 Influence of Q value on bandwidth in parallel resonance
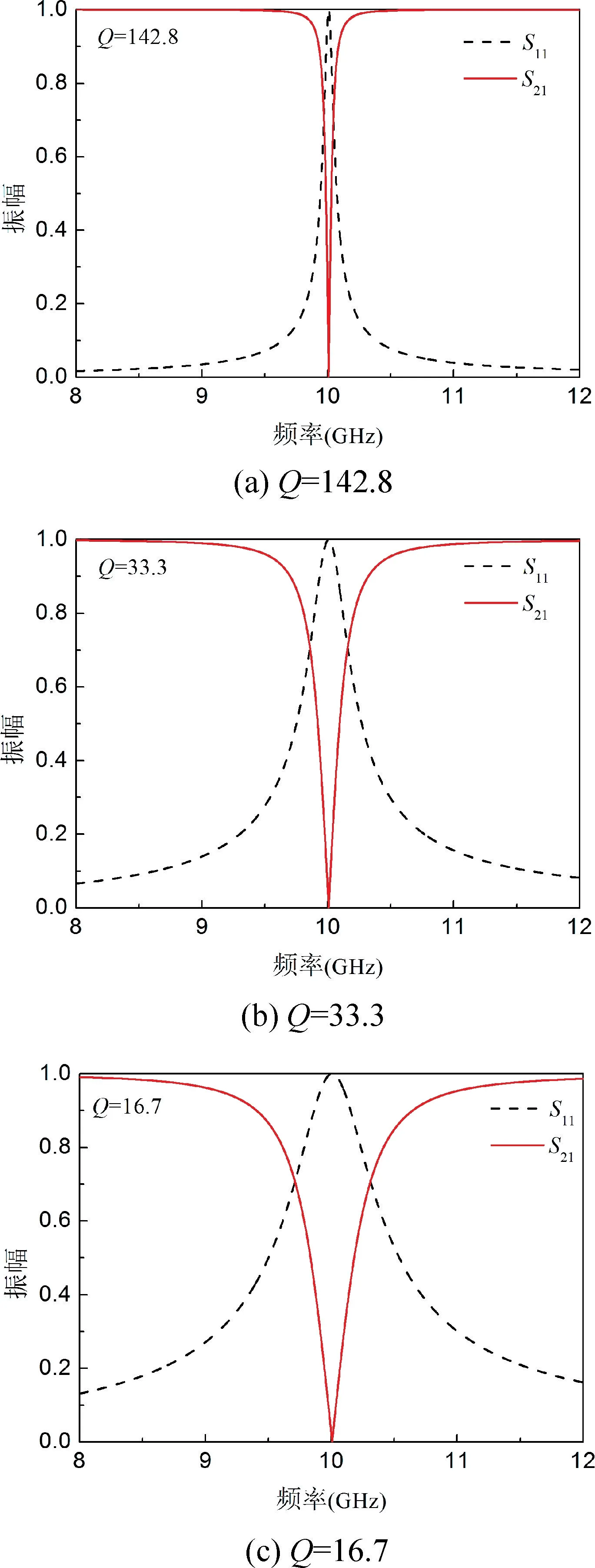
图4 串联谐振中的Q 值对带宽的影响Fig.4 Influence of Q value on bandwidth in series resonance
3 超材料完美吸收的二端口网络等效电路
在上述关于超材料全反射的二端口网络等效电路分析的基础上,接下来研究超材料完美吸收的二端口网络等效电路。对于无金属底板的超材料完美吸收单元结构而言,一般需要同时有电谐振结构和磁谐振结构,所以需要在串联支路和并联支路中同时引入LC谐振电路。另外,超材料对外界电磁能量的吸收都是由损耗引起的,所以还需要引入损耗电阻R。这里,损耗包括金属的损耗和介质材料的损耗。在微波频段,金属的损耗很小,损耗主要是由介质材料引起的。在并联及串联谐振中加入损耗电阻R 后,最终得到的等效电路如图5 所示。其中,图5(a)中串联谐振电路靠近负载端RL,图5(b)中并联谐振电路靠近负载端RL。首先,对图5 中等效电路的完美吸收条件进行定性分析,为简单起见,只在谐振状态下进行研究。这样,等效电路就变成一个纯电阻构成的网络。因为无反射是完美吸收的一个基本条件,所以,图5(a)中的电路从源端看进去,满足阻抗匹配的条件为:
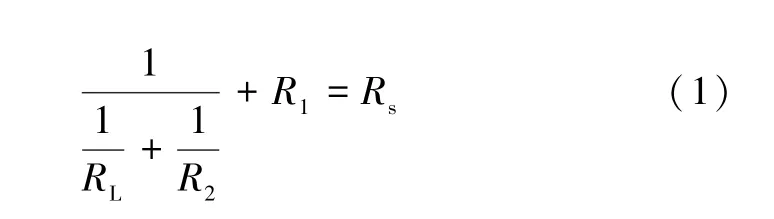
式(1)中代入相关数值可得:
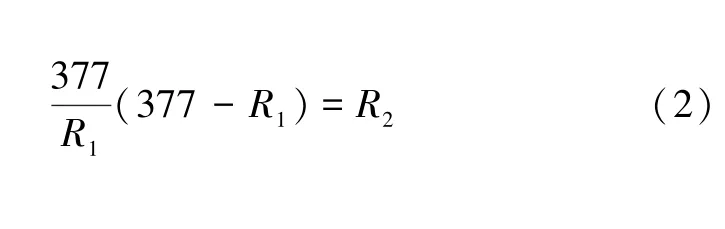
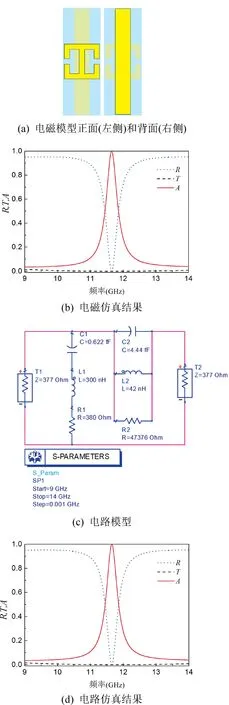
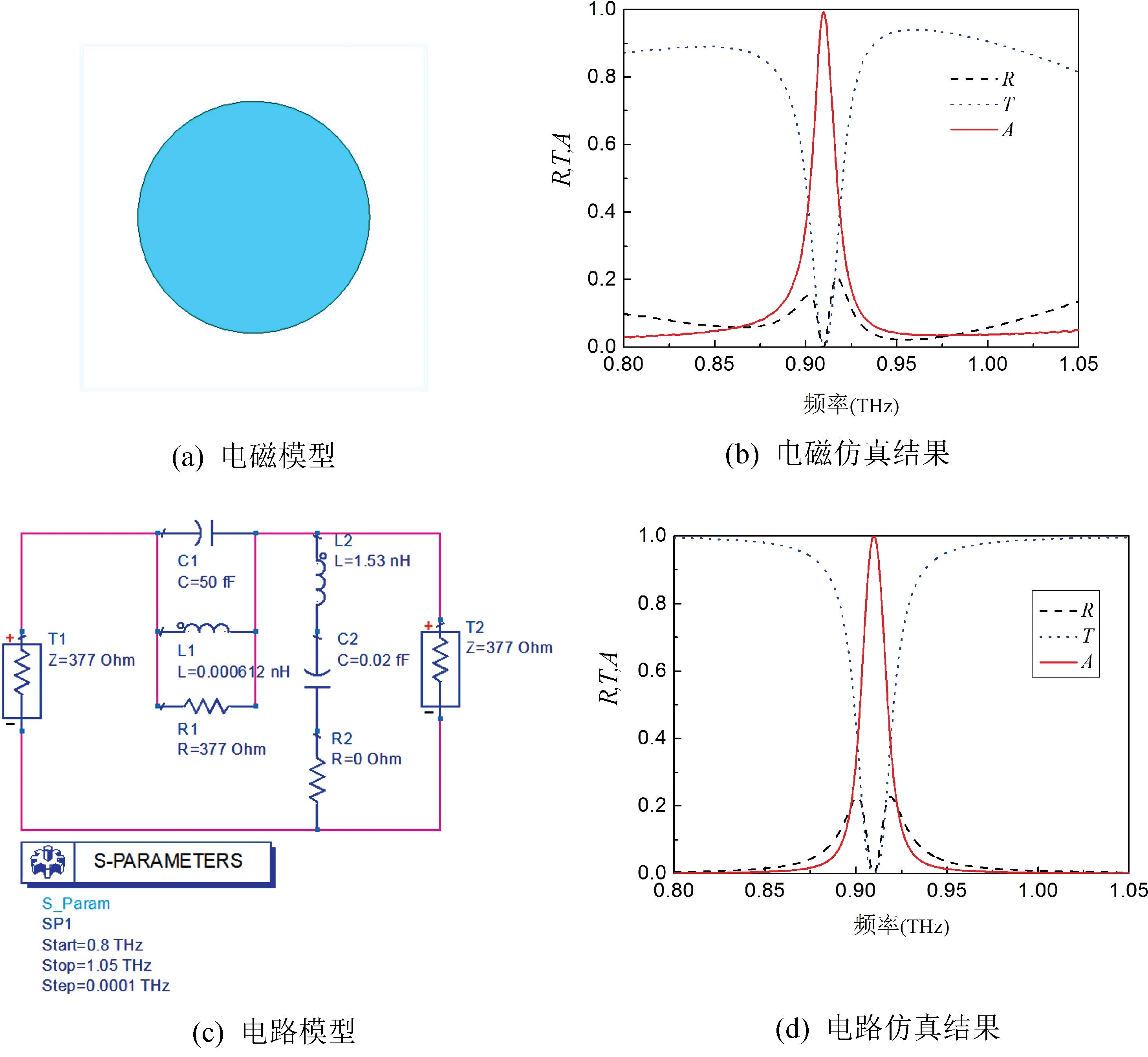
式(2)中,R1满足的条件为0 图5 超材料完美吸波的二端口网络等效电路Fig.5 Two-port network equivalent circuit for perfect absorption of metamaterials 式(3)中代入相关数值可得: 式(4)中,电阻R1满足的条件为R1>377 Ω。当R1取适当的值,使R2>>377 Ω,能够实现近似完美吸收。 接下来,以具体的超材料完美吸波器为例,建立等效电路模型并提取参数值。首先以金属结构超材料完美吸波器的代表性文献[4]为例,按照文中给出的单元结构参数值,采用电磁仿真软件CST 建立的模型如图6(a)所示,其中左侧为单元结构的正面图,右侧为单元结构的背面图。电磁模型仿真的反射率R、透射率T和吸收率A的结果如图6(b)所示,与文献[4]的结果完全一致(文献中透射率的纵坐标范围为0~0.05,本文为0~1)。根据图6(b)中整个频段透射率几乎为0 而反射率在谐振频率处为0 这一特点,结合上述电路完美吸波的定性分析可知,无金属底板吸波器应同时含有电谐振和磁谐振,LC 串联对应于电谐振,LC 并联对应于磁谐振,最终选用图5(b)的结构进行等效变换。电路仿真软件ADS 得到的等效电路及各元件参数值如图6(c)所示,其中代表源和负载的T1 和T2 端的电阻为377 Ω,其他的参数值也已在图中标明。电路仿真的反射率R、透射率T和吸收率A的结果如图6(d)所示,与电磁仿真结果(图6(b))几乎一致,说明了等效电路建模的正确性。 图6 金属结构超材料完美吸波的电磁和电路仿真Fig.6 Electromagnetic and circuit simulation of perfect absorption of metal structure metamaterial 接着以全介质型惠更斯超表面[9]为例,对不含有金属结构的超材料完美吸波器进行电磁模型和等效电路模型研究,其结果如图7 所示。金属结构的超材料单元中,一段金属线等效为电感,两金属片及二者的间隙等效为电容,损耗等效为电阻,等效电路中的各元件具有真实的物理含义。全介质型超材料的单元结构是由一定品质因数的介质谐振器镶嵌在衬底材料中构成的。采用等效电路模型,能够简单快速地对介质谐振器的谐振频率、带宽和损耗等行为进行描述,是电磁波与介质谐振单元结构相互作用等效分析的强有力手段。介质谐振器的磁谐振和电谐振是两个基本的谐振模态。惠更斯超表面完美吸收是通过对介质谐振器几何尺寸的调控使电谐振频率和磁谐振频率重叠,进而实现完美吸收。所以,在它的等效电路图中,引入两个LC 谐振支路,通过改变两个谐振支路中的电容和电感值,使LC 串联支路和LC 并联支路的谐振频率相等,进而实现完美吸收的条件。按照文献[9]中给出的单元结构尺寸,用电磁仿真软件CST 建立的以太赫兹波段石英晶体谐振器为单元结构的介质型超表面,如图7(a)所示,反射率R、透射率T和吸收率A的仿真结果如图7(b)所示,与文献[9]中的结果一致。根据图7(b)中透射率在谐振频率处为0 和反射率在整个频段都非常小的特点(与前一例金属结构超材料正好相反),结合上述电路完美吸收的定性分析,确定选用图5(a) 进行等效变换。采用电路仿真软件ADS得到的等效电路图及元件值如图7(c)所示,其中T1和T2 端的电阻为377 Ω,其他参数值也已在图中标明。电路仿真的反射率R、透射率T和吸收率A的结果如图7(d)所示,与电磁仿真结果图7(b)在吸收频率、带宽等方面基本一致。需要说明的是,在等效电路建模的过程中,只考虑了介质谐振器对吸收率的影响,并没有考虑衬底材料的影响,所以在离开谐振频率的低频和高频区域中,电路仿真结果和电磁仿真结果有一定的差异,可以通过加入电阻等元件对等效电路进行修正,这里不做讨论。 图7 全介质型超材料完美吸波的电磁和电路仿真Fig.7 Electromagnetic and circuit simulation of perfect absorption of all dielectric metamaterial 超材料完美吸收的单元结构可以通过加载金属底板实现。由于加载了金属底板,电磁波几乎不能透射,这时超材料完美吸收的等效电路就由二端口网络变为简单的一端口网络,相应地也有两种基本类型,如图8(a)所示的并联谐振型和图8(b)所示的串联谐振型,二者是等价的。很显然,在谐振频率处,并联型LC支路断开,串联型LC 支路短接,只要两种电路中的电阻R与源电阻Rs相等,即对应于超材料的等效阻抗与真空阻抗完全匹配,就能实现完美吸收。超材料完美吸收的一端口网络等效电路较为简单,具体的转化过程不再赘述,若有需要,可按照图2 中描述的规律对谐振频率和吸收带宽进行调控,从而完成含有金属底板的超材料完美吸波器的等效电路变换。 图8 超材料完美吸收的一端口网络等效电路Fig.8 One-port network equivalent circuit for perfect absorption of metamaterials 最后需要说明的是,谐振是超材料单元的一个基本属性。超材料单元实现谐振的途径比较多,如金属结构的LC 谐振和表面等离激元共振,介质结构的Mie谐振等。为了简单明了地理解超材料单元由谐振而产生的新机理和新现象,本文引入了等效电路描述的方式。所以,不管是哪一种具体的谐振方式,都可以用一个LC 等效电路描述其实现的新机理,如电谐振实现等效负介电常数、磁谐振实现等效负磁导率等。本文用等效电路描述超材料的完美吸收行为。由于吸收是伴随着反射和透射产生的,所以同时也给出了一端口和二端口模型反射和透射行为的等效电路描述。一般而言,一个具体的超材料单元会产生一系列不同的谐振模态,由于低频谐振模态对应的体积较小,所以关于超材料的研究大多集中在低频谐振模态,如电偶极子谐振模态和磁偶极子谐振模态。当然,也有一些研究者利用四极子谐振模态构造超材料单元。对于高阶谐振模态,也完全可以用LC 谐振电路进行描述,只需要修改其中的电感和电容参数即可。如果要在一个电路中同时反映出低频谐振模态和高频谐振模态,可以引入多个LC 谐振的方式,这时电路会变得略微复杂一点。 另外,在超材料完美吸波器的研制过程中,一些结构复杂、层数较多[16-17]的单元是为了引入更多的谐振实现多频及宽频带的要求,这些都可以通过增加并联或串联谐振电路的形式表示出来,从而实现多频及宽频带的等效电路模型。仅仅依靠一种LC 谐振的方式有一定局限性,它只适合窄带或单频吸收。 超材料完美吸波器单元结构的类型比较多,本文把含有金属底板的单元等效为一端口网络,把不含有金属底板的单元等效为二端口网络。用电谐振器和磁谐振器组成的单元以及介质型惠更斯超表面单元为例,分别用电路仿真软件ADS 和电磁仿真软件CST 计算了吸收效率、频率和带宽等指标,结果的一致性验证了等效电路模型及参数提取的正确性和有效性。通过超材料吸波单元等效电路模型的建立,有利于理解各种不同单元结构的吸波机理,还可以利用等效电路模型指导构建新型吸波单元结构。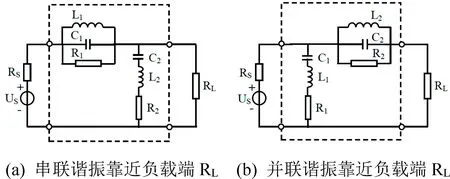
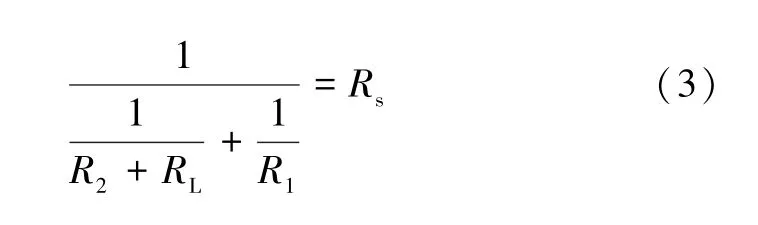
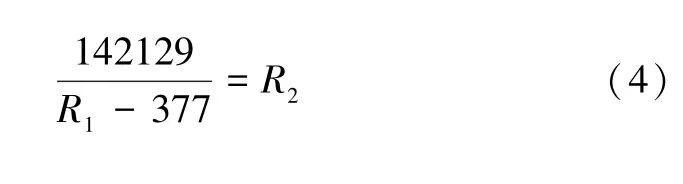
4 超材料完美吸收的一端口网络等效电路
5 结论

