迹-行列式平面中的分岔分析及实例

曹南斌张亚飞刘霞

(河北地质大学 数理教学部, 河北 石家庄 050031)

考虑平面线性系统

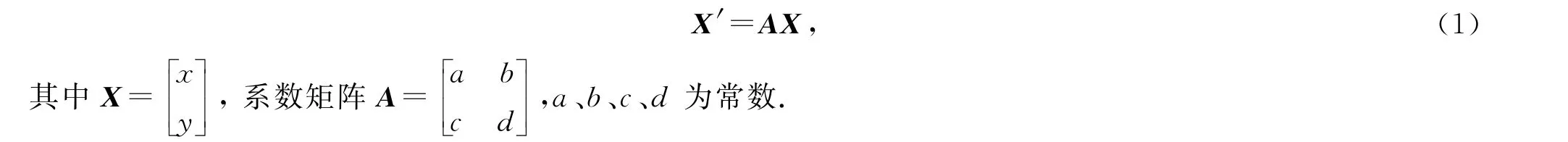
若记A的2个特征值为λ1、λ2, 迹为T=trA, 行列式为D=detA, 则由T=λ1+λ2,D=λ1·λ2,若已知T和D的值则完全可确定λ1、λ2的符号, 从而也就确定了平面系统(1)的几何特征.因此通过迹-行列式能够直观地将系统(1)的相图进行分类, 这在文献[1-3]中已经有过部分分析.

当系统(1)为双曲系统时,Hirsch等[1]对鞍点、(螺线)源点、(螺线)汇点已经有了详细的讨论.微分动力系统理论研究的最新进展, 特别是稳定性猜想的解决表明人们对于双曲系统的认识已趋于完善[4].当系统(1)为非双曲系统时, 即λ1、λ2中至少有1个实部为零时, 在实际中应用更为广泛, 如压电复合材料层合梁的动力学方程、计算机病毒传播模型等[5-6].因此对非双曲系统的研究愈来愈引人注目.例如,Hirsch等[1]讨论了λ1、λ2为纯虚数的情形；Lakshmanan等[2-3]详细讨论了当λ1、λ2中有1个为零或2个同时为零时的情形.本文在文献[1-3]的基础上给出了通过迹-行列式对系统(1)的完整分类,见图1.

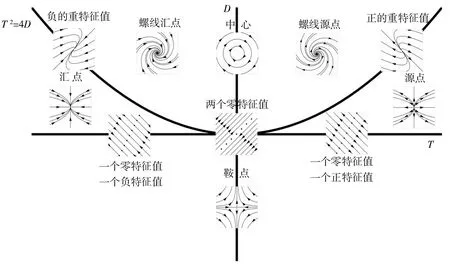
图1 迹-行列式平面[1]Fig.1 Trace-determinant plane

在图1中, 每一个坐标为(T,D)的点对应的是无穷多个不同的矩阵, 但这些矩阵有相同的迹和行列式, 从而有相同的特征值, 因此平面图上的每一个点就确定了以该矩阵为系数矩阵的系统解的几何特征.

进一步观察迹-行列式平面图可以发现系统(1)会发生分岔现象.当系统(1)含有1个参数时, 可以看作是1个单参数族, 这时系统(1)随着参数的变化对应于平面上的1条曲线, 当这条曲线穿过T轴、D轴的正半轴或者抛物线T2-4D=0时, 线性系统的相图就会产生分岔, 相应的几何形状将有很大变化.

1 基本概念

定义1[1]方程的常值解称为该方程的平衡解或平衡点.

定义2[1]若特征值λ1、λ2都有非零实部, 此时系统(1)被称为双曲系统；否则, 为非双曲系统.

定义3[1]若特征值λ1、λ2为实数, 且满足λ1＜0＜λ2时, 系统(1)的平衡点为鞍点；满足λ1＜λ2＜0时,系统(1)的平衡点为汇点；满足0＜λ1＜λ2时, 系统(1)的平衡点为源点.若特征值λ1、λ2为复数, 实部为0时, 系统(1)的平衡点为中心；实部为负数时, 系统(1)的平衡点为螺线汇点；实部为正数时, 系统(1)的平衡点为螺线源点.

定义4[7]

分岔是指系统的某一参数达到临界值时系统的行为发生突然变化的现象.

定义5[8]电阻在任一时刻的电压U与电流I的关系, 可用U-I平面上的一条曲线确定, 这条曲线称为电阻的特性曲线.特性曲线为通过坐标原点直线的电阻, 称为线性电阻；否则称为非线性电阻.其中, 电阻值R＞0的线性电阻称为线性正电阻(或无源电阻)；电阻值R＜0 的线性电阻称为线性负电阻(或有源电阻).

定义6[9]超导体材料指在某一温度下, 电阻突然降为0的材料.

2 实例分析

2.1 RLC电路中的Liénard系统

电子电路中常见的RLC电路, 是由1个电阻、1个电感、1个电容这3个支路相互连接构成的, 有电流通过每个支路, 如图2所示.下面重点讨论来自RLC电路的一类重要系统,著名的Liénard系统[10-12], 即

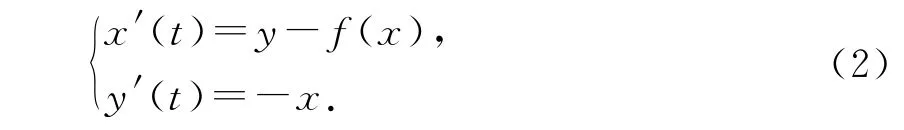
这里f可以是线性的, 也可以是非线性的.f的图像称为电阻的特性曲线.考虑f(x)=kx的线形情形.其中电阻特性f(x)依赖于参数k,k与电阻的温度有关.函数f满足条件f∶R→R连续且f(0)=0[13],则系统(2)可以转化为以下矩阵形式:

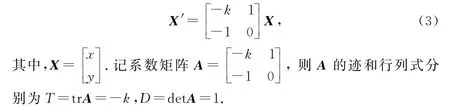
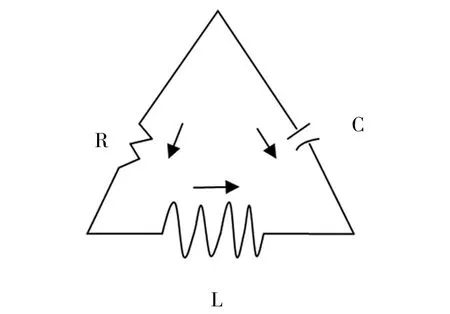
图2 RLC电路[1]Fig.2 RLC circuit

将k看作系统(3)的1个参数, 则随着k的取值, 可根据T2-4D的符号分为以下3种情形讨论:

1) 若T2-4D＞0, 即k＜-2或k＞2, 这时系统(3)有2个直线解.当k＜-2时, 原点为实的源点, 见图3a；当k＞2时, 原点为实的汇点, 见图3g；

图3 系统(3)的相图Fig.3 Phase portraits of system(3)

2) 若T2-4D=0, 即k=-2或k=2, 这时系统(3)只有一个直线解.当k=-2时, 原点是一个退化的源点, 见图3b；当k=2时, 原点是一个退化的汇点, 见图3f；

3) 若T2-4D＜0, 即-2＜k＜2.当-2＜k＜0时, 原点为螺线源点, 见图3c；当k=0时, 原点为中心, 见图3d；当0＜k＜2时, 原点为螺线汇点, 见图3e.

通过观察系统(3)的相图, 可见系统在k=-2时经历了一个分岔, 系统的平衡点从一个实的源点变化成退化的源点又变化成螺线源点；在k=0时经历的分岔,使系统的平衡点从一个螺线源点转化成中心又转化成螺线汇点；在k=2时经历的分岔,使平衡点从一个螺线汇点变化成退化的汇点又变化成实的汇点,见图3.

回到RLC电路本身,很容易描述电阻的物理行为:无源电阻的特性曲线落入第一、三象限；有源电阻的特性曲线落入第二、四象限[8].由上面的讨论可知,当k＞0时,电阻为无源电阻,系统所有解都趋向于原点,这就意味着随着时间的增加,电路中的电流和电压逐渐减弱直到变为零,电路需要消耗能量；当k=0时,电阻为超导体材料,系统所有解都在以原点为中心的圆周上,此时电路不损失电能也不产生电能；当k＜0时,此时电阻为有源电阻,系统所有解都远离原点,这就意味着随着时间的增加,电路中的电流和电压逐渐增强,此时电路不但不消耗能量,反而向外界输出能量.

2.2 调和振子的振动实验

如图4所示,在一个粗糙平面上,弹簧的左端固定在垂直的墙面上,右端与一个质量为m的小球相连.起始时,通过小球压缩弹簧到A位置,O点是弹簧保持原长时小球的位置,B点是释放小球后小球向右运动到的最远位置,C点是小球从B点弹回向左运动到的最远位置.用x(t)代表弹簧的压缩量或伸长量,于是x′(t)就是小球运动的速度,x″(t)为加速度.释放小球后研究小球在水平方向上的受力和运动情况,可知小球受到一个正比于x(t)的弹性回复力与一个正比于x′(t)的摩擦力.因此,小球受到的合力可表示为F=px+qx′.根据牛顿第二定律,该调和振子实验的微分方程可以表示为

为了简单起见,下令m=1,记x′(t)为v(t),则方程(4)可以改写为以下矩阵形式:

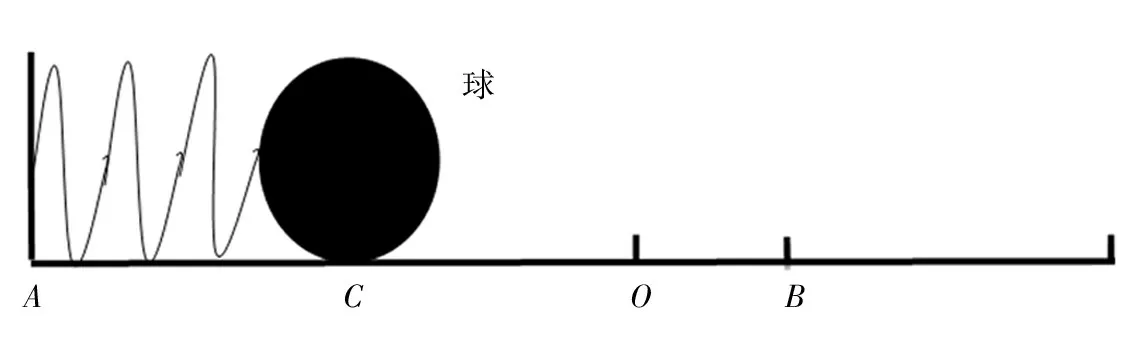
图4 一个调和振子的振动实验Fig.4 Oscillation test of a harmonic oscillator

在本实验中规定向右为正方向,弹簧的弹性系数为k(k＞0),平面的阻尼系数为b(b＞0).

在AO之间,小球受到向右的弹力kx和向左的摩擦力-bv,因此合力F=kx-bv(p=k＞0,q=-b),系统(5)的平衡点(0,0)为鞍点,相图见图5a；小球运动至O点时,此时小球只受到向左的摩擦力-bv,因此合力F=-bv(p=0,q=-b),此时系统(5)的系数矩阵有一个零特征值和一个负的实特征值,见图5b；小球从O点继续运动至B点,受到的合力F=-kx-bv(p=-k＜0,q=-b),此时系统的平衡点(0,0)为汇点,见图5c.

由上面的分析可见,小球从A到B的运动过程中,q值固定不变,p随着小球的运动从正值变为负值.如果将p看作一个参数,则系统(5)在p=0时经历了一个分岔,原点从一个鞍点变成汇点,其稳定性发生了根本性的变化,见图5.从调和振子本身来说,这意味着小球在该运动过程中在O点处发生了“质”的改变.

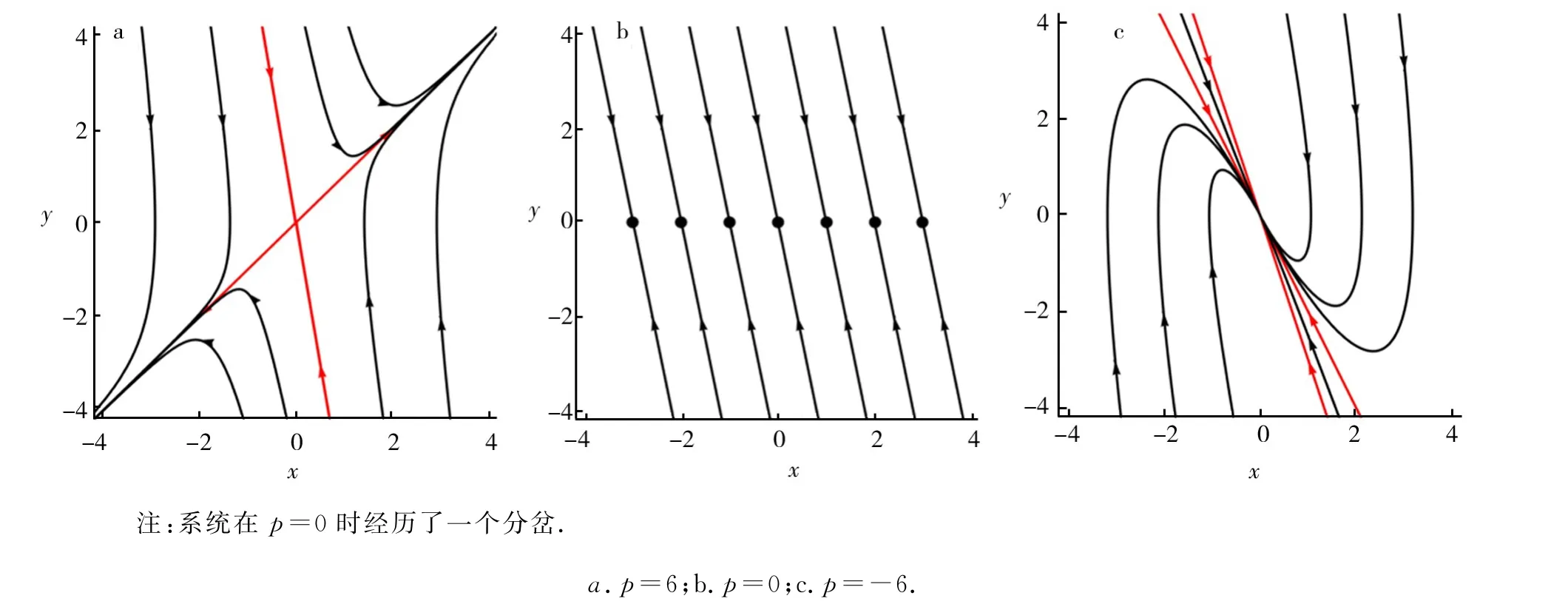
图5 q=-5时系统(5)的相图Fig.5 Portraits of system(5)when q=-5

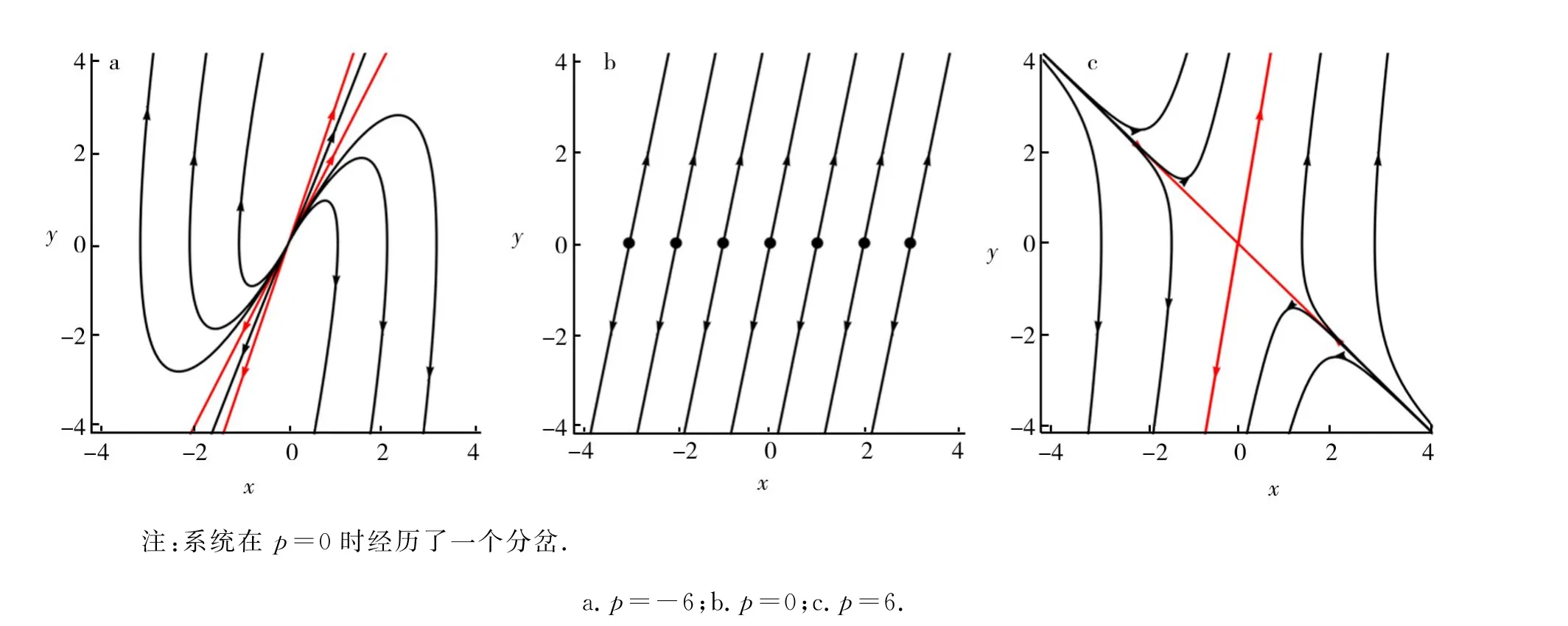
图6 当q=5时系统(5)的相图Fig.6 Phase portraits of system(5)when q=5

类似于前面的分析,小球从B点运动至C点的过程中,q不变,随着p的变化,系统在p=0时经历了一个分岔,(0,0)从一个源点变成一个鞍点,见图6.之所以会发生以上2种分岔,这在物理上也不难解释.通过O点时小球受到的其中一个主要外力——弹力方向发生了改变,从而运动规律也就有所变化.特别地,在O点时弹力为零,因此是该分岔的临界状态.

3 结论

本文主要给出了根据迹-行列式对平面线性系统的完整分类,并且以电路系统中的Liénard系统和调和振子为例,讨论了迹-行列式平面图中所有出现的分岔.