基于小波熵的心音信号去噪算法研究

刘倩，徐彦，夏斌，柳兆军

(1.山东理工大学 计算机科学与技术学院， 山东 淄博 255049；2.山东省淄博市中医医院 心血管病科， 山东 淄博 255300)

心音是心脏运动过程中所发出的声音，鉴于其产生机制，干净的心音信号蕴含了大量的心脏健康状况方面的信息，在评估心脏功能状况中发挥了重要的作用。但从人体采集的心音信号往往特别微弱，在采集的过程中易受到来自身体内部和外界的干扰而不可避免地混入噪声。所以心音信号用于医疗诊断分析之前必须先要消除其中的噪声[1]。目前常用的心音去噪算法有经验模态分解去噪算法[2-3]和小波去噪算法[4-7]等。基于经验模态分解的去噪算法简单地将心音信号分解为不同频段的固有模态，再根据心音信号所处的频段特点，舍掉一部分高频信号，该方法往往在去除噪声的同时，也会去掉一部分心音信号。对于传统的小波去噪算法，在低信噪比的情况下，不能根据噪声和信号的特性选取阈值，易去噪过度，导致最终去噪效果不甚理想。周克良等[8]通过蚁群算法全局搜索最小均方误差下的阈值，提高了信噪比，但蚁群的初始赋值是阈值选取关键。信息论中，熵用来描述信源的不确定度和信源中每个符号包含的平均信息量，它可表征信号潜在动态过程的有用信息，即信号的概率分布可由熵值大小来表征。系统的不确定性越大，则熵值越大，反之，不确定性越小，熵值越小。基于信息熵理论，本文提出一种基于小波变换和熵值理论[9-11]的自适应阈值算法进行心音信号去噪，利用信号的噪声特性，选取小波高频系数子带区间中最大的小波熵值估计阈值，以此实现心音信号的有效提取。

1 心音信号的小波阈值去噪理论

1.1 心音信号的特点

心音信号主要频率在600 Hz 以内，在医学上通常把心音分为第一心音(S1)、第二心音(S2)、第三心音(S3)和第四心音(S4)。S1 和S2主要的频率范围是 50～110 Hz[12]，因此通过人耳就可以听见。在大多数情况下只能听到第一心音和第二心音，但在某些健康的青年和儿童身上也能听到第三心音，而第四心音偶尔也能够听到。正常心音信号如图1所示。

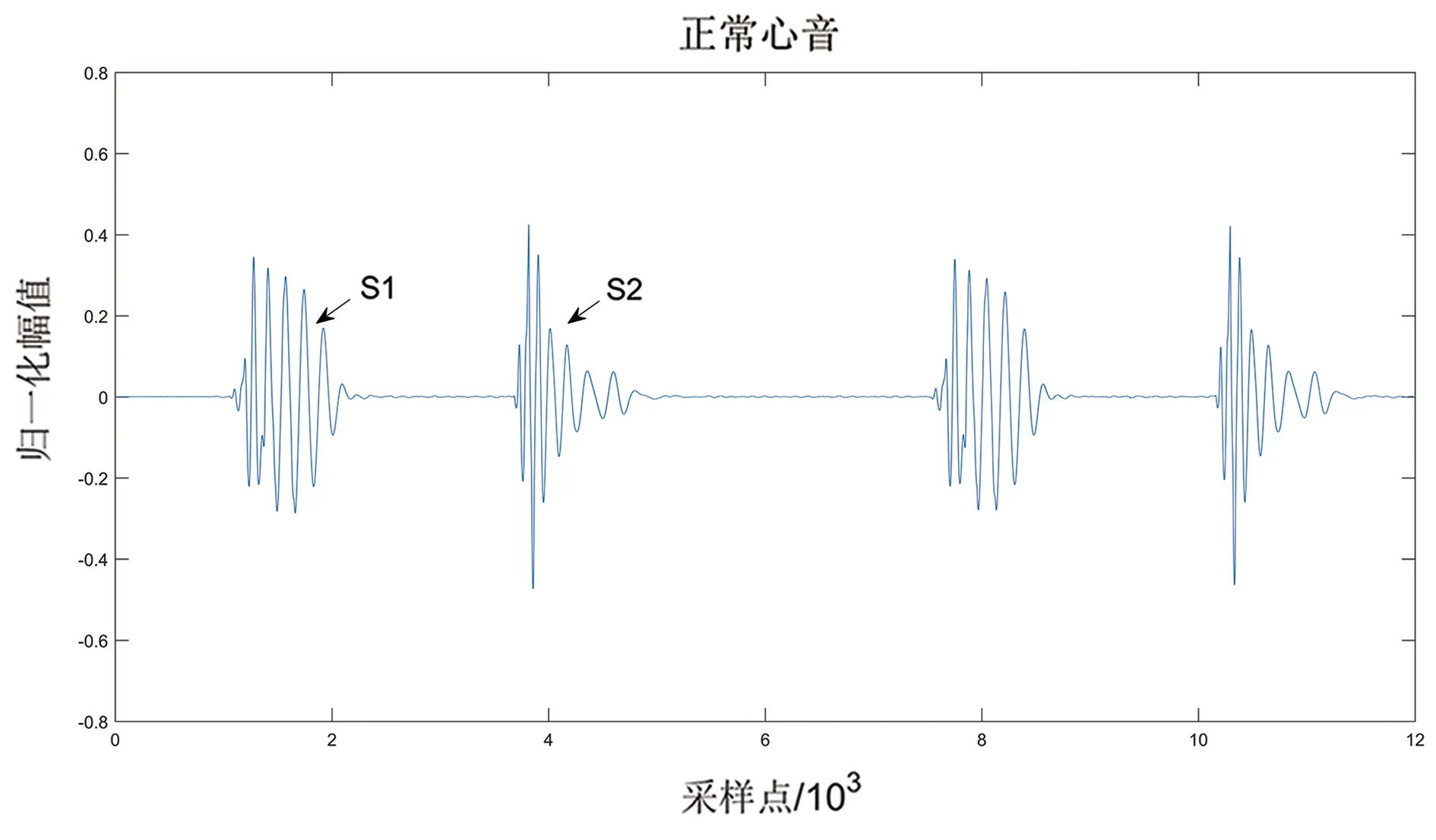
图1 正常心音信号

1.2 小波阈值去噪理论

小波[13]是一种持续时间很短的波，小波必须满足以下容许条件：

(1)

满足式(1)的时间函数ψ(t)称为母小波或基本小波。将母小波伸缩和平移之后得到函数族：

(2)

式中：a为伸缩参数或尺度参数；b为平移参数。

对任一能量有限信号f(t)，其连续小波变换定义为

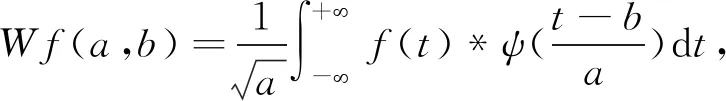
(3)

经过小波变换后，信号的能量高度集中于少量幅度较大的小波系数，而噪声由于其随机性，能量却比较均匀地分布于变换域，所以小波变换用简单的阈值判别法保留大幅值分解系数的同时亦能最大限度地抑制噪声。

心音信号的小波变换阈值去噪算法如下：

1)对于采集的含噪的心音信号f(t)，选取合适的小波基函数，并根据心音信号频率，选择分解层数，得到不同层次的小波系数；

2)对于小波系数选择合适的阈值进行去噪；

3)对去噪后的心音信号进行重构，得到去噪的心音信号。

根据小波阈值去噪理论发现，阈值的选取决定心音信号的去噪效果。

2 基于小波熵的心音信号去噪算法

2.1 小波熵的理论基础

在信息论中熵描述的是随机变量的不确定程度，熵越大则越混乱。小波熵理论是基于小波分析方法建立类似信息熵的理论， 能够对时频域上能量分布特性进行定量描述。小波变换后的心音信号，各个尺度上的噪声随机性大、熵值高，因此，通过小波熵自适应地确定各个尺度上的阈值，实现噪声的有效滤除。

当小波基是一组正交基时，小波变换的Parseval定理为

(4)

式中cj,k称为心音信号f(t)的小波系数。由式(4)可知，经小波分解后，任一尺度的小波能量为该尺度小波系数的平方和，即

(5)

信号的总能量为

(6)

把每一尺度上的小波系数作为独立的信号源，假设小波系数共有N个采样点，将小波系数cj,k等分为n个小区间，其中第i个子区间的小波系数能量为

(7)

而第i个子区间的能量占该尺度的总能量的概率为

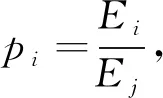
(8)

则第i个子区间的小波熵定义[14]为

(9)

2.2 阈值选取

本文阈值采用Donoho[4]提出的阈值计算公式，即

(10)

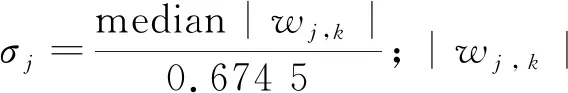
2.3 算法流程

本文提出的去噪算法流程如图2所示。首先对含噪的心音信号进行小波分解；然后对每一尺度上的小波高频系数等分N个区间，根据式(5)—式(9)，计算每个区间的小波熵，选取小波熵值最大区间的小波高频系数中值作为该尺度的噪声方差，计算该尺度上的阈值；最后将小波变换的低频分量和经过小波熵阈值去噪后的高频分量重构， 实现心音信号的最终去噪。

3 仿真结果与分析

3.1 去噪效果分析

仿真实验输入信噪比为5 dB的心音信号，采用小波熵阈值、小波固定阈值和极大极小阈值分别对正常心音信号、第二心音分裂及含S4的心音信号去噪处理，采用的小波函数为sym4并进行6层小波分解，去噪效果分别如图3—图5所示。

图3 正常心音去噪算法效果图

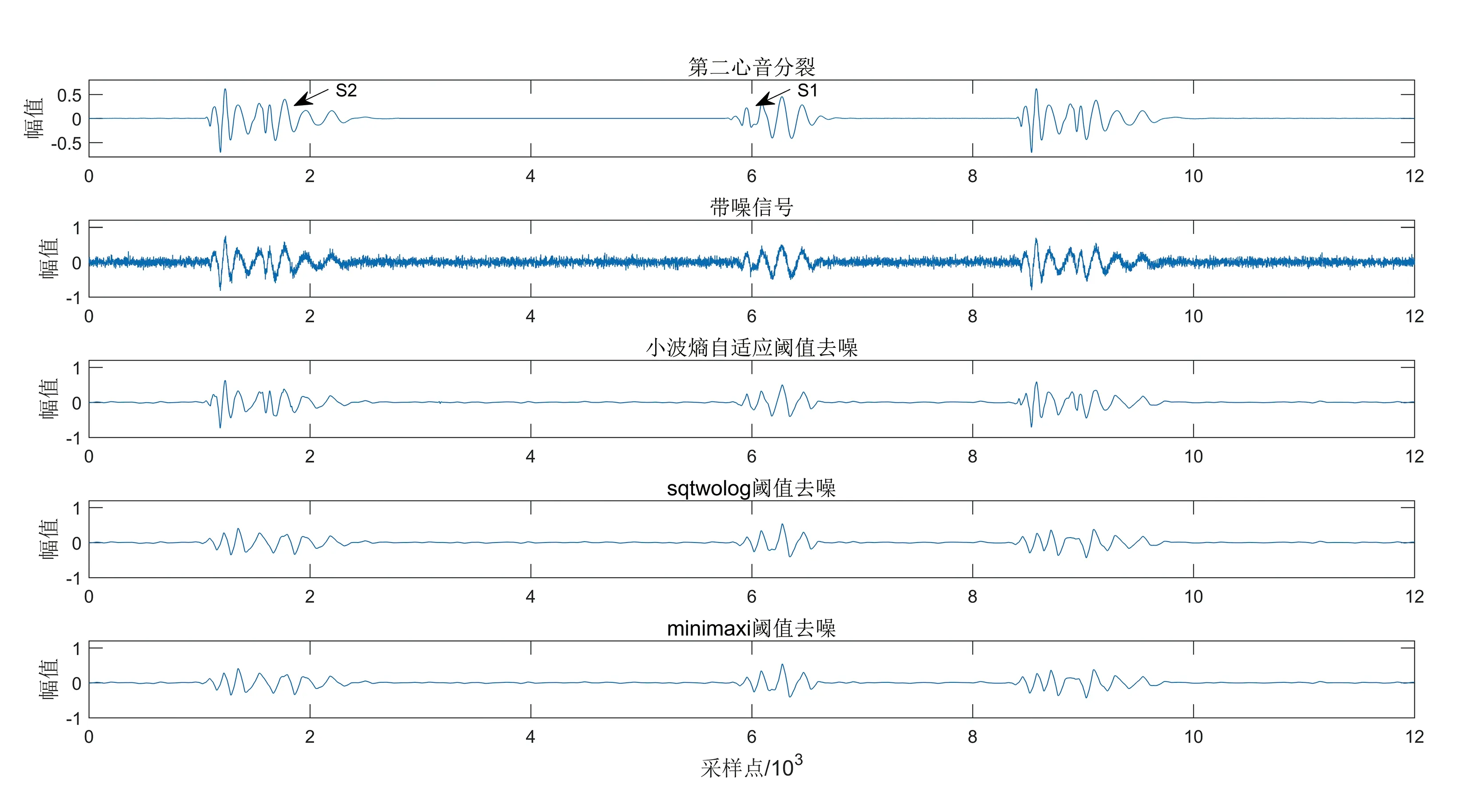
图 4 第二心音分裂去噪算法效果图

图5 含S4的心音信号去噪算法效果图

由图3可知，在S1S2、S2S1区间小波熵算法较其他两种算法的噪声滤除效果更好，而且对于原心音的S1和S2的特征保留更为完善。

图4采用三种阈值算法对第二心音分裂信号去噪处理，三种算法对于分裂音的特征都保留比较完好，但小波熵阈值对于分裂音的幅值没有削弱，而且在S1S2和S2S1区间的噪声剔除得更为干净，更加利于后续心音信号的特征提取。

图5采用三种阈值算法对含有S4的心音信号去噪，可以看出经小波熵算法去噪后，第四心音的特征与未加噪声之前的信号特征基本一致，优于其他两种算法，能为后续心脏的诊断提供更准确的信息。

3.2 去噪效果评价

为了更清晰客观地分析不同阈值去噪算法的去噪效果，本文分别采用信噪比(SNR)和均方根误差(RMSE)对三种阈值算法进行评价。其中，信噪比越高说明去噪效果越好；均方根误差越小，说明与原心音信号越接近。

仿真实验采用信噪比分别在-5、0、5和10 dB条件下的正常心音信号，并在同一信噪比下重复运行100次实验，分别求取输出信噪比及均方根误差的平均值。图6是心音信号的输入输出信噪比曲线，图7是输出信号的均方根误差曲线。

图6 心音信号输入输出信噪比曲线

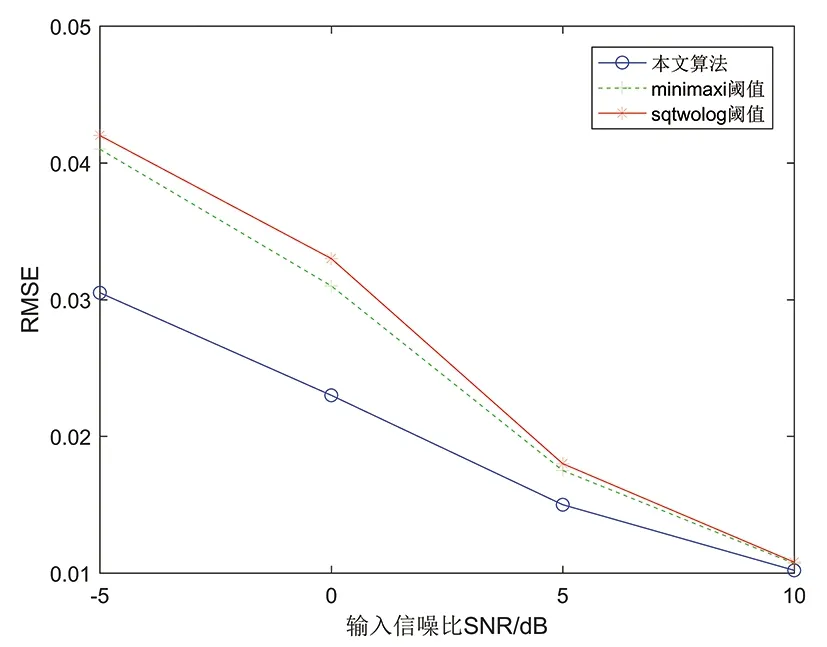
图7 均方根误差曲线

由图6和图7可知，在-5、0和5 dB低信噪比条件下，本文算法输出的信噪比明显高于其他两种小波阈值算法，而RMSE低于其他两种算法，去噪效果较好。随着信噪比的提高，输入信噪比为10 dB时，本文算法的性能与极大极小阈值算法相近，皆优于固定阈值算法。从去噪性能分析，本文算法>极大极小阈值算法>固定阈值算法。综合上述结果，在同一输入信噪比条件下，本文算法可以更加有效地剔除噪声而保留原心音信号的特征。

4 结论

1)心音信号由于其非平稳性，在传统去噪算法中常用小波阈值去噪，该算法简单，但阈值的选取决定着最终的去噪效果。本文采用小波变换与熵值结合的算法，根据小波变换后不同尺度的高频系数熵值特性来自适应地选取阈值。

2)将本文采用的阈值算法和传统的小波固定阈值、极大极小阈值算法在同一输入信噪比下，分别对正常心音、第二心音分裂及含S4的心音去噪处理。仿真结果表明，本文算法能够去掉噪声的同时尽可能地保留了原心音的信号特征，去噪效果比较明显。

3)在不同输入信噪比条件下，采用三种算法对正常心音信号去噪处理，结果表明，本文算法的输出信噪比比传统的小波阈值去噪算法的高，而均方根误差低，为后续的心音信号处理提供了参考。