基于加速残差网络的图像超分辨率重建方法

梁 敏，王昊榕，张 瑶，李 杰

（山西财经大学信息学院，太原 030006）

（*通信作者电子邮箱liangmin716@163.com）

0 引言

图像在采集、传输过程中受设备、光照等环境影响，直接降低了图像的质量。数字图像超分辨率（Super-Resolution，SR）旨在通过某种模型约束条件由低分辨率（Low Resolution，LR）图像重建清晰的高分辨率（High Resolution，HR）图像，在公共安全、视频监控、医学图像处理［1-3］等方面具有强烈的需求。但根据有限的图像信息重建出更多信息是一个病态过程，所以图像超分辨率重建研究始终是一个具有挑战性的任务。

目前，图像超分辨率重建是前沿热门领域，吸引了越来越多的学者参与研究，并发表了众多有意义的工作，其中，具有代表性的有：Yang 等［4］提出的基于稀疏编码表示的超分辨率方 法（Sparse-coding-based Super-Resolution，ScSR），Timofte等［5］提出的可调整锚定邻域回归方法（Adjusted Anchored neighborhood regression for fast super-resolution，A+）。近年来，基于深度学习的超分辨率方法表现出良好的性能。Dong等［6］提出了基于卷积神经网络的图像超分辨率重建（Super-Resolution using Convolutional Neural Network，SRCNN）方法，将卷积神经网络应用于超分辨率，实现了以低分辨率图像作为输入、高分辨率图像作为输出的端到端映射的重建模型。Wang 等［7］将传统的稀疏编码模型与深度学习相结合，提出了基于稀疏编码的网络（Sparse-Coding-based Network，SCN）。Dong 等［8］修改了SRCNN 模型，提出了加速的超分辨率卷积神经网络（Fast Super-Resolution Convolutional Neural Network，FSRCNN），通过在网络末端添加反卷积层替代SRCNN初始上采样操作，使得不同比例缩放因子可以共享卷积层权重，提升了重建速度。Kim 等［9］应用残差学习并结合可调梯度裁剪策略提出了超深卷积神经网络的图像超分辨率方法（Super-Resolution using Very Deep convolutional network，VDSR）。李现国等［10］设计了具有中间层监督的网络模型（Intermediate Supervision Convolutional Neural Network，ISCNN），借助监督层误差函数来改善网络梯度消失现象。刘月峰等［11］先对低分辨率图像进行三种插值操作，然后进行五种不同强度的锐化操作，最后将图像合并排列成三维矩阵，以此作为网络的多通道输入。Wang 等［12］设计了一个通过深层和浅层卷积网络实现端到端映射的超分辨率模型（End-to-End Deep and Shallow convolutional network，EEDS），由浅层通道重建图像的主要结构，深层通道重建图像的高频细节。上述方法仍存在的问题是：浅层网络不能充分提取图像的特征，有重建质量不高的天然缺陷；而深层网络参数量大、计算复杂度高、重建效率低。

针对上述问题，本文提出一种基于加速残差网络的图像超分辨率重建方法（image Super-Resolution reconstruction method based on AccelerateD residual network，ADSR）。该方法对低分辨率图像与高分辨率图像之间的高频残差信息运用加速残差网络进行训练，将低分辨率图像与网络学到的残差相加得到重建图像。主要贡献包括：

1）构建一个残差网络对低分辨率图像与高分辨率图像之间的高频残差信息进行重建，避免低分辨率图像携带的低频信息在深层网络中的冗余学习，将网络主要用于高频残差信息的训练，从而提高效率。

2）在非线性映射前加入收缩层，对提取的低分辨率图像的特征图维数进行降维，能够减少深层网络参数，提高时间效率，以较少的网络参数快速获得较好的重建质量。

3）探索ADSR 网络模型在运动模糊图像超分辨率重建上的有效性，在多种模糊核下均取得了较现有方法更好的视觉效果和客观量化指标。

1 ADSR网络

为了解决利用深层网络进行超分辨率重建中存在的网络参数多、计算复杂度高等问题，本文构建了一个ADSR 网络模型。在本章中，将其视为由低分辨率图像到高分辨率图像的端到端映射过程，并划分为六部分介绍：低分辨率特征提取、特征收缩、非线性映射、高分辨率特征扩展、高频残差信息重建以及残差求和。图1给出了ADSR的网络框架。ADSR整体是一个残差网络，其主要目的是对低分辨率图像缺失的高频细节部分进行重建，提高边缘及纹理信息的重建精度。在局部上将端到端的非线性映射部分更细致地划分成特征收缩、非线性映射、高分辨率特征扩展这三个部分，降低了深层网络传输过程中低分辨率特征图的维度，从而降低模型复杂度。

图1 ADSR网络架构Fig.1 ADSR network architecture

1.1 低分辨率特征提取

单幅低分辨率图像重建时，首先将该低分辨率图像采用双三次插值方法（Bicubic）上采样到要重建的高分辨率图像尺寸，得到初始的上采样低分辨率图像Y作为网络的输入，网络的目标是将Y尽可能地恢复出与真值高分辨率图像X相似的重建图像Z。利用一组滤波器对低分辨率图像Y进行卷积操作提取出丰富的图像特征，其中每一个滤波器对应得到一张特征图。将该层结构表示为F1(Y)=W1*Y+B1，W1和B1分别表示滤波器的权重以及偏差，“*”表示卷积操作，W1对应n1个尺寸为f1×f1 的滤波器，即经过特征提取层能够提取出n1张特征图。该部分如图1中的Patch extraction所示。

1.2 特征收缩

在超分辨率重建任务中，把从低分辨率特征提取层F1提取到的特征图进行非线性映射得到用于重建高分辨率图像对应的高分辨率特征图。然而在特征提取层中为了获得图像的丰富特征，特征维数n1通常较大，再将这些特征传入多层非线性映射结构时会产生较多的参数，时间复杂度较高。

ADSR在非线性映射前加入了特征收缩层将特征图维数从n1 维降至n2 维。该层结构表示为F2(Y)=W2*F1(Y) +B2，W2和B2分别表示滤波器的权重以及偏差，W2对应n2个尺寸为f2 ×f2 的滤波器，且n2＜n1，即经过特征收缩层将特征图维数降至n2。该部分如图1中的Shrinking所示。

1.3 非线性映射

通过低分辨率特征提取及特征收缩后得到了低分辨率图像的n2 张特征图，将这些特征图进行非线性映射能够得到用于重建高分辨率图像对应的高分辨率特征图，所以非线性映射结构对重建质量发挥着关键的作用。ADSR 使用多层小尺寸滤波器串联的架构来获得较大的图像感受野，有利于提高重建质量。将非线性映射部分的当前层数表示为i，其结构表示如式（1）所示：

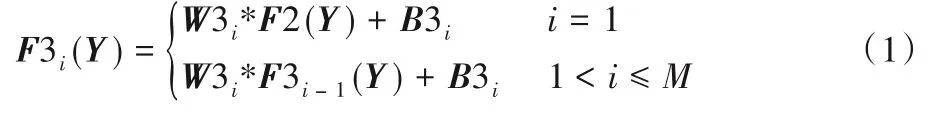
其中：W3i和B3i表示第i层滤波器的权重以及偏差，M表示非线性映射部分的总层数，其值将在实验部分讨论确定。该部分如图1中的Mapping所示。

1.4 高分辨率特征扩展

为了减少网络参数，在非线性映射前应用了特征收缩层进行降维，但直接使用n2 维特征进行重建得到的图像质量不高，所以要在非线性映射之后、重建之前加入扩展层将特征图维数从n2维升回至n1维。表示为F4(Y)=W4*F3i(Y) +B4，其中i=M，W4和B4分别表示滤波器的权重以及偏差，W4对应n1 个尺寸为f4 ×f4 的滤波器，即经过特征扩展层将高分辨率特征图维数升至n1。该部分如图1中的Expanding所示。

1.5 高频残差信息重建

深层超分辨率重建网络主要完成两个任务：一是将低分辨率图像Y已有的信息从网络层的输入端输送至输出端；二是重建低分辨率图像与真值高分辨率图像之间的差值部分R，即R=X-Y。在超分辨率重建任务中，要重建的信息远少于低分辨率和高分辨率图像已有的公共信息，所以任务一将耗费网络极大的资源，而真正用于任务二的资源较少。另外输入端信息Y在网络中进行传输学习时随着网络结构加深，容易出现细节丢失的问题。

ADSR 构建了一个残差网络对低分辨率图像与高分辨率图像之间的高频残差信息进行重建。残差结构能够避免信息Y的深层网络传送过程，将网络主要用在高频残差信息R的重建上。ADSR 将n1维高分辨率特征图进行融合生成的一维图像，即为重建出的高频残差图像。表示为R′=W5*F4(Y) +B5，W5和B5分别表示滤波器的权重以及偏差，W5对应1个尺寸为f5×f5的滤波器。该部分如图1中Reconstruction所示。

1.6 残差求和

本文构建的残差网络框架在训练时以上采样低分辨率图像Y作为输入，将由残差网络获得的高频残差图像R′与低分辨率图像Y相加得到的重建高分辨率图像Z作为输出，以均方误差（Mean Squared Error，MSE）作为网络模型的损失函数，如式（2）所示，式中n表示训练集的样本数目。

图2显示了set5数据集中butterfly图像的上采样低分辨率图像Y，重建的残差图像R′以及最终生成的高分辨率图像Z。

图2 butterfly图像超分辨率重建过程Fig.2 Super-resolution reconstruction process of butterfly image

综上所述，基于加速残差网络的图像超分辨率重建方法的过程如图3所示，分为以下步骤：

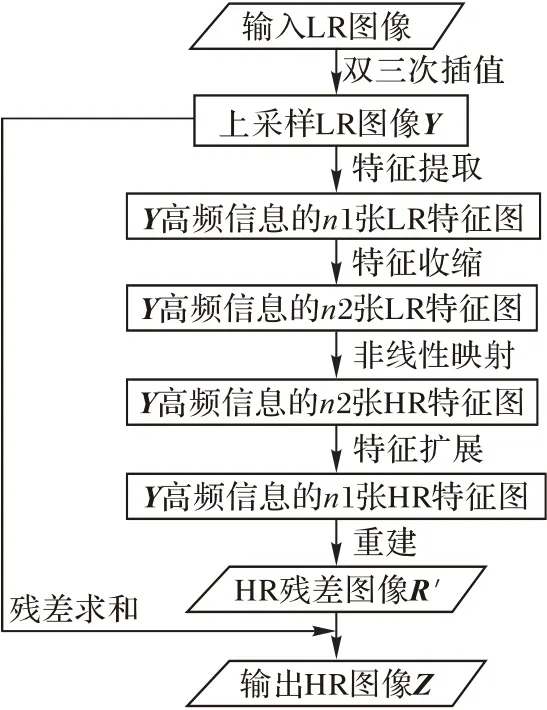
图3 ADSR技术路线Fig.3 ADSR technology roadmap

1）对输入的低分辨率图像进行双三次插值处理，获得上采样的低分辨率图像Y；

2）提取代表图像Y高频信息的n1张低分辨率特征图；

3）通过特征收缩层将其降维至n2；

4）经过非线性映射层得到对应的n2张高分辨率特征图；

5）通过特征扩展层将其升维至n1；

6）由n1张高分辨率特征图重建出高分辨率残差图像R′；

7）将R′与Y相加获得最终重建的高分辨率图像Z。

2 实验

2.1 实现细节

2.1.1 训练集与测试集

训练集 本文实验基于随机森林学习（Random Forest Learning，RFL）［13］的超分辨率方法使用的291 张图片，采用数据增强的方法，对图像旋转90°、180°、270°，并缩小0.6倍以及0.8倍，得到3 492张图片作为训练集。采用43的步长将数据集切割成43×43的图像块，混合多比例因子2、3、4数据集将获得大约38万张的图像块用于网络训练。

测试集采用set5［14］、set14［15］、BSD100［16］以 及Urban100［17］四个数据集作为测试集。

2.1.2 训练细节

ADSR 网络结构以MSE 作为损失函数，表示重建的高分辨率图像与真值图像之间的差异，选用Adam（Adam optimization）算法来优化损失函数。训练的初始学习率设置为0.000 1，权重衰减系数设置为0.000 1，滤波器的权重采用He 等［18］提出的方法进行初始化。训练的批大小设置为128，模型训练了超过200 个epoch。网络在硬件参数NVIDIA GeForce GTX 1060 下使用caffe 工具以及Matlab R2017b 接口进行训练及测试。

2.1.3 评价指标

为了定量表示重建结果并与其他方法进行对比，本文采用峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）及结构相似性（Structural SIMilarity，SSIM）作为重建效果评价标准。PSNR 值越大代表与真值图像相比重建图像失真越少，SSIM值越大代表重建图像与真值图像的结构相似性越高。

2.2 网络参数设置研究

2.2.1 不同层数设置

ADSR 加入特征收缩层减少网络参数势必会以降低重建质量为代价，所以考虑增加网络层数来降低质量的损失，因此设置了实验对合适的网络层数进行探讨，先以22 层网络结构作为基础，之后通过增加M讨论选定ADSR最终的层数。

表1 显示了ADSR 在n1=64、n2=32，网络层数分别为22、23、24、25以及26的各测试集的PSNR 及SSIM 均值结果（其中加粗表示最高值）。通过分析不同层数的重建结果，选定层数较小且重建质量较好的24层为默认的层数。

表1 测试集在不同层数设置下的PSNR及SSIM均值Tab.1 Mean values of PSNR/SSIM of test sets under different layer configurations

2.2.2 不同滤波器个数设置

本文将低分辨率特征提取部分的滤波器个数n1 设置为64，即通过特征提取层提取出代表低分辨率图像特征的64 张特征图。在进行收缩时考虑将其降为16 维、32 维以及48 维。表2 显示了在24 层网络架构上（n1，n2）设置为（64，16）、（64，32）及（64，48）的各测试集的PSNR 及SSIM 均值结果（其中加粗的值表示最高值）。通过分析不同设置下的重建结果，选定重建质量较好的（64，48）为默认的滤波器个数。

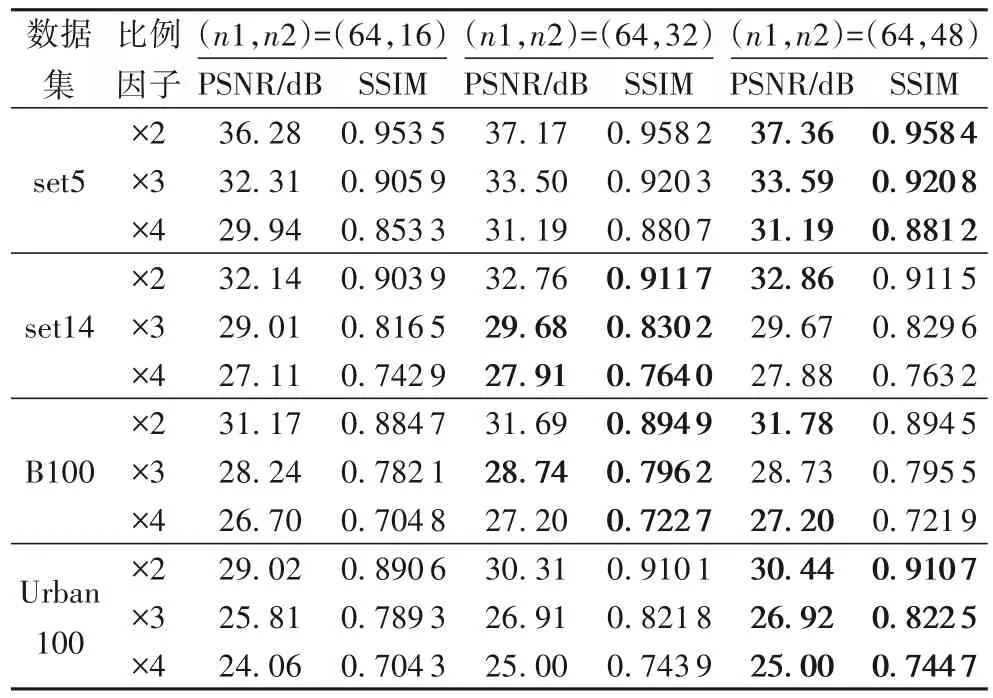
表2 测试集在不同滤波器个数n1、n2设置下的PSNR及SSIM均值Tab.2 Mean values of PSNR/SSIM of test sets under different filter number n1，n2 configurations

2.2.3 不同比例因子设置

为解决一个神经网络模型只适用于单一比例因子的问题，本文将原始训练集按多种倍数比例因子进行缩放并融合成大的训练集，使得训练得到的模型适用于所有训练集中包含的比例因子，提高网络模型的泛化能力。表3和表4显示了层数为24，滤波器个数为（64，48）的网络结构在不同训练集下得到的模型的set5 数据集的PSNR 及SSIM 结果，其中加粗的值表示测试比例因子包含在训练集的比例因子中。

表4 不同比例因子模型对SSIM均值的影响Tab.4 The influence of different scale factor models on mean value of SSIM

实验结果显示单比例因子训练集的模型无法处理其他比例因子重建问题，有时重建效果甚至比双三次插值方法效果还差。以缩放比例因子2 下的测试集重建结果为例，其在比例因子2 训练集的模型下的PSNR 值为37.55，在比例因子3训练集的模型下的PSNR 值为30.92，在比例因子4 训练集的模型下的PSNR 值为25.67，而用双三次插值方法得到的PSNR值为33.66。

相比单比例因子训练集来说，混合比例因子训练集下的模型可以有效处理所有预定义比例因子的重建问题，且能使大比例因子测试集的重建效果得到增强。以表3中（×2，3，4）训练集模型下的各尺度PSNR 值与对应的各单比例因子训练集的模型的PSNR 值对比为例：37.36（×2，3，4）-37.55（×2）、33.59（×2，3，4）-33.47（×3）、31.19（×2，3，4）-31.00（×4）。

表3 不同比例因子模型对PSNR均值的影响Tab.3 Influence of different scale factor models on mean value of PSNR

另外对于大比例因子3 和4 来说训练集涉及的预定义比例因子越多，模型重建的增强效果就越明显。以缩放比例因子4下的测试集重建结果为例，其在单比例因子4训练集的模型下的PSNR 值为31.00，在混合比例因子（×2，4）训练集的模型下的PSNR 值为31.14，（×3，4）训练集的模型下的PSNR 值为31.06，（×2，3，4）训练集的模型下的PSNR值为31.19。

2.3 与现有方法比较

2.3.1 重建质量的比较

为了反映ADSR 的重建效果，本文将它与Bicubic、ScSR［4］、A+［5］以及近来国内外提出的基于深度学习的方法SRCNN［6］、SCN［7］、FSRCNN［8］、VDSR［9］、ISCNN［10］、刘月峰等［11］方法以及EEDS［12］进行比较。其中，所有对比方法的重建结果都使用原作者提供的数据或原作者发布的源代码生成的数据。本文方法选择在层数为24、滤波器个数为（64，48）、数据集为（×2，3，4）混合比例因子融合下的重建结果。图4列出了set14数据集中comic图像在比例因子为3时多种方法下的重建图像以及PSNR 值。从中可以看出，ADSR 方法在边缘处及高频细节处的重建效果更为突出，且整体结构与原图更为接近。

图4 comic在比例因子为3时的重建图像Fig.4 Reconstructed image of comic at the scale of 3

表5、6 分别显示了ADSR 与这些方法在set5、set14、B100及Urban100 四个测试集下的PSNR 和SSIM 均值，其中加粗标注的值表示最高值，下划线标注的值表示次高值。结果显示在重建质量上ADSR除稍低于VDSR外，均优于对比方法。

表5 ADSR与现有方法PSNR的比较 单位：dB Tab.5 Comparison of PSNR of ADSR with existing methods unit：dB

表6 ADSR与现有方法SSIM的比较Tab.6 Comparison of SSIM of ADSR with existing methods

VDSR 的PSNR 及SSIM 均值略高于本文方法，其原因是它直接使用提取出的高维度特征图进行非线性映射，网络模型参数量比ADSR 大（2.36 MB＞1.50 MB）。ADSR 采用的特征降维操作会产生较小的重建质量的损失，但能在时间效率上取得较大的优势。图5 列出了ADSR 与VDSR 这两种方法在4 个测试集上的重建质量与重建时间的对比，结果显示ADSR 方法的PSNR 均值只比VDSR 低0.1 dB 左右，但重建速度提高了将近一倍。

图5 VDSR与ADSR重建质量与时间的对比Fig.5 Comparison of reconstruction quality and time between VDSR and ADSR

另外，虽然ADSR 在测试集上的重建均值略低，但能在很多图像上取得比VDSR 好的重建结果，如图6 所示，列出了set5数据集中bird图像及set14数据集中flowers图像在比例因子为3 时两种方法下的重建图像以及PSNR 值对比，其中ADSR取得了更佳的重建结果。

图6 Bird及flowers在比例因子为3时的重建图像Fig.6 Reconstructed images of bird and flowers at the scale of 3

2.3.2 重建时间的比较

为了反映ADSR 的深层网络加速效果，本文与A+［5］、SRCNN［6］、VDSR［9］、ISCNN［10］以及基于对称残差卷积神经网络的图像超分辨率重建方法（Super-Resolution based on Symmetric residual convolution neural network，SymSR）［19］进行了重建时间的比较。表7 显示了ADSR 与这些方法在set5、set14、B100 以及Urban100 测试集下的重建时间均值，其中加粗标注的值表示最低值。结果显示ADSR 的重建速度最快。在set5、set14、B100 三个数据集上ADSR 的重建速度至少是SRCNN 的20 倍，是VDSR 深层网络的1.5 倍。在具有重建挑战性的城市数据集Urban100 上ADSR 的重建速度至少是SRCNN 的43 倍，是VDSR 深层网络的2.5 倍。另外ADSR 网络模型参数量较VDSR 有所减小（1.50 MB＜2.36 MB），说明了本文方法达到了减少网络参数，降低网络复杂度，且明显提高重建速度的目的。

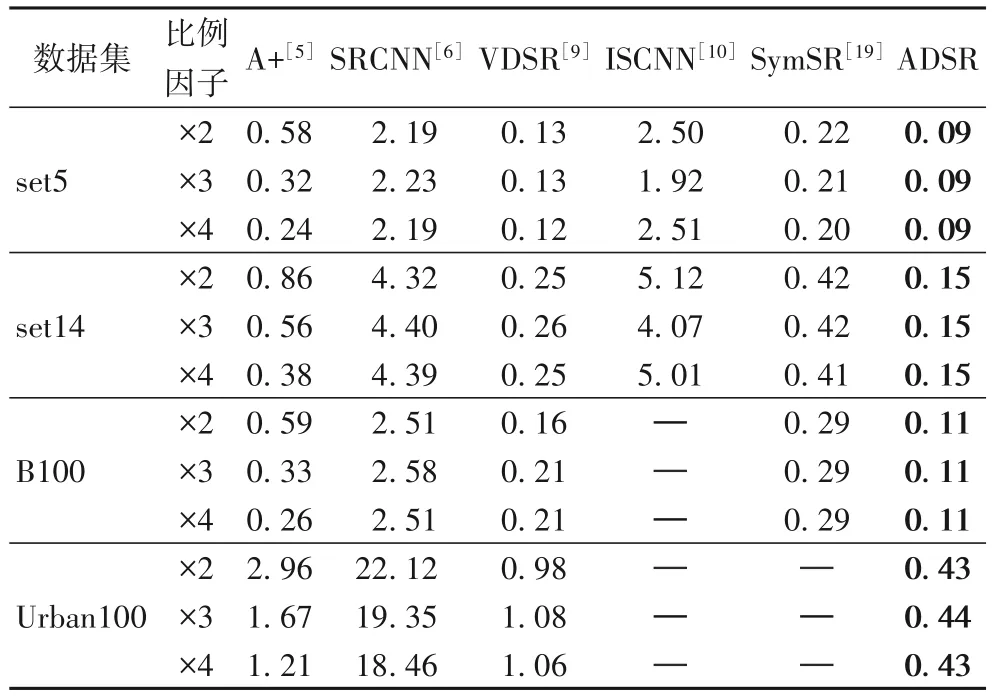
表7 ADSR与现有方法重建时间的比较 单位：sTab.7 Comparison of reconstruction time of ADSR with other methods unit：s

2.4 ADSR模型处理运动模糊的有效性

目前对图像超分辨率重建的研究绝大多数是集中在处理下采样模糊的理想化退化模型，鲜有研究考虑运动模糊等更为一般的退化因素［20］。本文将ADSR 应用在处理运动模糊这一具有挑战性的问题上，探索ADSR 模型在处理运动模糊时的有效性。

训练集将多种运动模糊核考虑在内，提升网络模型的泛化能力，其中模糊长度设置为［5，8，11，14］，模糊角度设置为［0°，45°］。图7列出了测试集中的3张图像在模糊长度为14，模糊角度为45°下的重建图像以及PSNR值，结果显示，与VDSR相比，ADSR能以较小的网络模型获得更优的重建效果，说明在处理运动模糊图像超分辨率重建问题上ADSR更有效。

图7 VDSR与ADSR重建质量的比较Fig.7 Comparison of reconstruction quality between VDSR and ADSR

图8列出了这两种方法在4个测试集上的重建时间对比，结果显示ADSR方法的重建速度比VDSR快将近一倍。

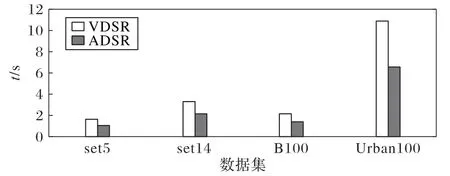
图8 VDSR与ADSR重建时间的比较Fig.8 Comparison of reconstruction time between VDSR and ADSR

3 结语

本文提出了一种基于加速残差网络的图像超分辨率重建方法ADSR。该方法对低分辨率图像与真值图像之间的残差信息进行重建，它在多层小尺寸滤波器串联的非线性映射结构前加入特征收缩层对提取的特征图维数进行降维，然后在映射后加入高分辨率特征扩展层进行升维，重建出高分辨率的残差信息。经实验证明，ADSR 能够取得较A+等传统方法以及SRCNN、ISCNN 等国内外深度学习方法更好的超分辨率重建结果，并且能够减少深层网络参数，降低网络复杂度，达到加快重建速度、提高重建效率的目的。此外将该方法应用于运动模糊图像的超分辨率重建也获得了较好的性能，但实际获取的低分辨率图像降质因素众多，后续将构建更高效的网络来处理通用降质模型下的低分辨率图像的超分辨率重建问题。