云边环境下基于博弈论的两阶段任务迁移策略

王艺洁，凡佳飞，王陈宇

（1.山东科技大学计算机科学与工程学院，山东青岛 266000；2.空装驻上海地区军事代表局空装驻南京地区第三军事代表室，南京 211100）

（*通信作者电子邮箱wyj_jsj@163.com）

0 引言

随着物联网（Internet of Things，IoT）的发展，移动设备的数量激增，具有沉浸式体验的移动应用程序正在逐渐流行，并成为5G［1］网络中的主流应用程序，丰富的应用程序规模也变得越来越大，比如自然语言处理［2］、虚拟现实［3］、智能交通［4］、车辆互联网［5］等，但这些新型应用程序需要大计算量和高能耗，而受轻量级移动设备的限制，计算密集型应用和计算资源有限的移动设备之间的冲突为未来物联网的发展带来了巨大挑战［6］。

为了解决移动设备资源有限以及延迟的问题，移动边缘计算（Mobile Edge Computing，MEC）［7-8］被提出。移动边缘计算可以在紧邻移动设备的无线接入网络内提供云计算能力，同时能够满足物联网应用的延迟要求［9］并提高物联网移动设备的可靠性和能效，因此在过去的几年时间出现了许多有关MEC 任务迁移的研究工作。Liu 等［10］提出Stackelberg 动态博弈模型，通过研究具有一个接入点（Access Point，AP）和许多其他无线设备的物联网应用的无线MEC 系统中的资源分配问题来获得节点的最佳分配资源；Chen 等［11］研究在多信道无线干扰环境下的移动边缘云计算的多用户迁移问题，将移动设备之间的分布式计算迁移决策问题转化为任务迁移博弈，但它未考虑到MEC 存在计算资源不足的可能性；文献［12］中建立博弈模型并使用变分不等式理论计算静态混合策略的任务均衡分配，通过分散算法用于在附近设备和边缘云之间分配计算任务，但它并未考虑到任务之间的信号干扰；Zheng等［13］研究动态环境下移动计算的多用户计算迁移问题，并提出多智能体随机学习算法保证收敛速度达到纳什均衡。Liu等［14］研究了在车辆边缘网络中多车辆计算迁移问题，通过计算迁移博弈来减少车辆计算开销，但仍需进一步研究车辆数与整体开销的关系。

由于大多数有关MEC 计算迁移的研究工作仅仅考虑移动设备和MEC 服务器之间的资源分配［15］，而没有考虑到集中式云计算（Centralized Cloud Computing，CCC）服务器［16］强大的计算能力和丰富的计算资源。而MEC 虽然可以减少处理延迟，改善用户体验，但是对于大量的物联网移动设备和移动应用程序的增加，MEC 服务器的资源瓶颈变得逐渐明显，尤其要考虑网络运营商的资本支出与运营支出；另一方面，物联网移动设备在与云进行数据交换时有可能经历较长的等待时间，但集中云可以为用户提供精确的云处理能力。可以说MEC 与云是互补的，因此充分利用移动设备、MEC 和CCC 的计算资源进行计算迁移是值得考虑的一个重要举措。近两年以来，边缘计算和云计算的关系变得清晰，二者并非互斥关系，而是相互融合。边缘计算解决了云原生应用的供应问题，成为云计算在未来发展的一个重要落地支撑，从而来到“云边协同”的新阶段。

基于上述的问题，本文研究了多通道无线干扰环境下MEC 资源受限的多用户任务迁移问题，并提出了一种用于物联网系统中移动边缘和云中心协同的计算资源分配机制［17］，为物联网移动设备提供强大的混合云平台，使得MEC 与集中式云共存。本文的目标是确定物联网移动设备的任务迁移决策。通过考虑移动设备的各异性，建立任务迁移模型满足多用户的任务迁移需求，提出了一种基于博弈论的两阶段任务迁移策略，以分布式的方式实现高效任务迁移。

1 系统模型

任务迁移考虑MEC 服务器和云中心服务器协同工作的范例。范例中包含一组移动设备、MEC 和CCC。在云边协同环境下提供一种优化解决方案，使得移动设备的成本开销能达到一个近似最优的结果。

1.1 通信模型

假设在云边协同系统下有N个移动设备，表示为N={1，2，…，N}。通过无线基站部署MEC 服务器，移动设备可以通过无线接入点（Wireless Access Point，WAP）与MEC 连接通信，将移动设备的计算任务迁移到MEC 服务器上执行。而无线基站有K条信道，这里的K个信道可以表示为K={1，2，…，K}。MEC 服务器拥有有限的计算资源，将MEC 的计算资源记为S。如果任务过多，可以通过有线连接的主干网迁移到集中式的云中心服务器执行，本文假设云中心拥有无限的计算资源。而移动设备的每一个计算任务需要两阶段的任务迁移决策：第一阶段是在移动设备端，设备首先决定是本地执行还是MEC 服务器执行；第二阶段即在选择MEC 执行后，当任务到达MEC 服务器发现资源不够需要排队，则决定是加入等待队列还是继续迁移到云中心服务器执行。

用符号an表示第n个移动设备的决策结果，其中an={0}∪K：an=0代表计算任务由移动设备本地执行；an=k表示移动设备n的计算任务通过信道an迁移到MEC 服务器上执行。在第二阶段的决策结果可以用符号yn表示，yn∈{0，1}：当yn=0时，表示计算任务继续迁移到集中式云服务器执行；当yn=1 时，表示计算任务在MEC 上执行，MEC 资源不够，任务也会排队继续等待执行。此时，根据两个阶段能够得到两个决策向量α=(a1，a2，…，an)和ψ=(y1，y2，…，yn)。假设移动设备n通过信道k访问MEC 服务器，则数据传输速率如式（1）［18］所示：

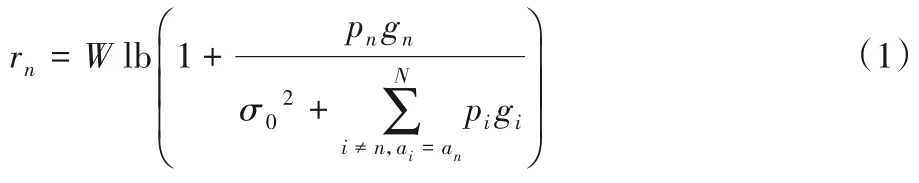
其中：W是信道带宽，pn是n的传输功率，gn是n和基站之间的信道增益，σ0

2是背景噪声功率。

在进行第二阶段的任务迁移时，MEC 与CCC 通过主干网进行有线连接。本文使用rec表示二者之间的数据传输速率，同时假设这一速率是恒定不变的。

1.2 任务迁移博弈计算模型

移动设备n的计算任务，可以将其定义为Tn≜(bn，qn)，其中bn是计算任务Tn所需的输入数据量，qn是完成计算任务所需的总计算能力（即CPU 周期数量），本文将计算能耗和计算时间两部分加权之和当作执行任务的总成本开销。

1.2.1 本地计算模型

当n选择本地计算时，总成本开销包括两部分：任务本地执行的时间和计算能耗。这里计算任务的执行时间为，执行任务的能耗为其中代表移动设备n的计算能力（即每秒的CPU 周期数）是每个CPU 周期的能耗系数。为了保证移动设备的能耗和执行延迟最小，在本模型中制定一个能耗和延迟的加权和，并将其命名为开销成本。因此本地执行的总开销成本为：

其中：λt和λe分别是移动设备n执行延迟和能耗的权重系数，并且这两个系数满足λt+λe=1 且0 ≤λt，λe≤1。不同的场景具有不同的特征，也应该对应不同的加权参数，以此来反映不同研究场景的一般需求。

1.2.2 MEC计算模型

对于迁移到MEC的任务，延迟包括将任务传送给MEC服务器的时间和在服务器上完成任务所需的计算时间。前者包括无线接口的传输时间以及移动设备与服务器之间的往返延迟。与文献［19］相同，本文忽略了将计算结果发送回设备的延迟开销，因为与传入的数据相比，密集的计算任务产生的结果数据大小被认为非常小。在任务迁移阶段，传输任务需要时间以及会消耗能量，因此传输任务的延迟是任务的处理延迟是其中表示为MEC 服务器分配给移动设备n的计算能力（即每秒的CPU 周期数）。因此总延迟是处理延迟和传输延迟之和，即为

1.2.3 CCC计算模型

经过第一阶段的决策，移动设备将任务迁移到MEC 服务器，若此时MEC 服务器的计算资源不足够，则移动设备需要决定继续排队等待任务执行还是迁移到CCC 服务器上执行。如果第二阶段移动设备选择将任务迁移到云服务器执行，那么整体的延迟包括任务从MEC 传输到CCC 的延迟以及在云中心执行的延迟。传输延迟为执行延迟为因此总延迟是其中f c是中心云服务器的计算能力，这里认为其为定值。综上所述，将第一阶段和第二阶段的决策相结合可以得到总成本开销为：

当在MEC 服务器上执行时yn=1，即成本开销由迁移到MEC服务器的延迟与能耗组成；当yn=0时，总成本开销由迁移到云服务器的延迟与能耗组成。

根据通信和计算模型可以发现，当选择将计算任务迁移至MEC 服务器时，每个移动设备的成本开销不仅取决于自己的迁移策略，还取决于其他移动设备的策略。如果太多移动设备选择相同的策略（即相同的无线信道）来迁移任务，那么迁移率会很低，并导致更多计算成本（包括更长的传输时间以及更高的能耗），这种情况下可能移动设备进行本地计算对自己会更有益。由于不同移动设备之间的相互影响关系，可以通过博弈论来进行建模和分析用户的迁移决策从而进行计算迁移。但是由于移动设备的状态是动态变化的，移动设备之间无法互相了解对方的状态，而且移动设备更喜欢通过速度快的信道来降低其成本开销，但是无线信道是随着时间变化的，这使得问题更具有挑战性。

2 任务迁移博弈

博弈论（Game Theory，GT）可以用来分析需要相互协作才能实现自己目标的多个非合作实体之间的交互。由于每个实体的需求不同，并不会追求相同的利益，因此在每个参与者选择最佳策略来达到自己的利益最大化时，都需要一个分散的策略。本文考虑利用每个移动设备的智能，以低复杂度来制定分散方案。文献［20］中证明了资源分配问题类似于最大装箱问题，被认为是NP（Non-deterministic Polynomial）难的。在博弈论中，所有的参与者进行自我调节从而达到一种互相满意的状态，使得任何参与者都没有动机单方面偏离，这能够减轻实施更为复杂的集中式系统的负担。假设在执行任务期间移动设备数量不会变，并且考虑一个准静态场景，在一个时隙内状态不变，但在不同的时隙内状态是有所改变的。

2.1 博弈公式化

定义集合a-n=(a1，a2，…，an-1，an+1，…，aN)作为除移动设备n以外其他移动设备的任务迁移决策。当给定其他设备的决策a-n，移动设备n选择合适的策略an使得自身总成本开销最小，即Cn(an，a-n)，∀n∈N。Cn(an，a-n)是n的成本开销函数，那么移动设备n总开销定义为：

将问题转化为博弈模型G=(N，{An}n∈N，{Cn}n∈N)，其中N 是移动设备集合，An是移动设备n的博弈策略集。接下来引入最佳响应策略的概念，以更好地获得所有设备的决策。

定义1给定了除移动设备n以外的其他设备的策略a-n，则移动设备n的最佳响应策略为：

表明所选择的an是可以最小化移动设备n成本开销的决策。

将任务迁移到MEC 服务器上是否成本开销会低于本地执行的成本，很大程度取决于其受到的来自其他移动设备的干扰，从引理1 可以找到通过干扰阈值来判断任务迁移到MEC服务器是否对移动设备是有益的。

引理1给定计算迁移博弈中除了移动设备n以外其他设备的策略a-n，如果n在所选的无线信道上（an≥1）所受到来自其他设备的干扰满足Fn(a) ≤THn，那么n的迁移是可以降低成本开销的，即称移动设备n的迁移是有益的任务迁移，其中阈值THn满足：

证明 在计算阈值时只需要考虑迁移到MEC 服务器的情况，而不需要考虑迁移到云服务器的情况，即yn=1。若要移动设备n的迁移是有益的迁移，必须满足迁移到MEC 服务器的开销成本小于本地执行成本。根据式（3）和（4），以及可以得到：

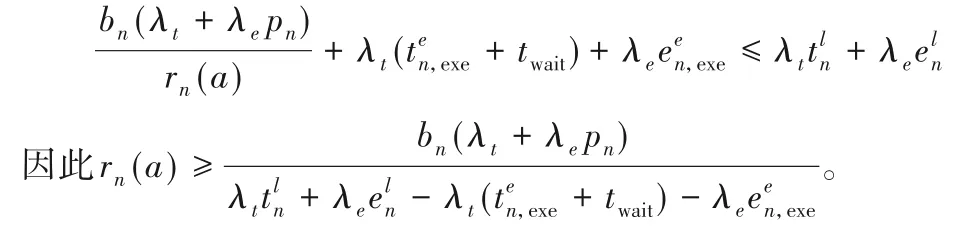
根据数据速率公式可以得到：

即Fn(a)≤THn。

根据引理1 可知，当n在无线信道上受到的干扰足够小时，将任务迁移到MEC 服务器上的成本开销会小于本地执行开销成本，即将任务迁移到MEC 服务器对移动设备来说是有益的，否则移动设备应该在本地执行任务。

当移动设备的任务完成第一阶段的决策迁移到MEC 后，需要决定其仍在MEC 执行或是迁移到CCC 执行，yn可以通过以下计算得到：

在博弈论中，纳什均衡（Nash Equilibrium，NE）是分析多个非合作实体决策互动结果的重要解决方案。接下来首先引入纳什均衡的概念。

定义2对于所有的移动设备，迁移策略集合a*=是非合作博弈G的一个纳什均衡，当且仅当它是最佳响应的固定点，即对于∀an∈An，n∈N，有：

纳什均衡具有自我稳定的特性，这意味着没有任何一个移动设备有动机单方面背离NE，因为移动设备无法通过采取不同于NE的策略来进一步降低成本开销。

2.2 博弈性质

为了证明博弈G存在NE 并最终证明博弈的收敛性，接下来要引入势博弈的概念。

定义3如果博弈G=(N，{An}n∈N，{Cn}n∈N)存在一个势函数P，满足：α=(a1，a2，…，an) →R，对∀n∈N，an，有≤Cn(an，a-n)，那 么≤P(an，a-n)，则称这个博弈为势博弈。

已知势博弈存在纳什均衡并且具有有限的改进特性，任何改进过程都可以在有限次的改进步骤后终止。因此只需要证明博弈G=(N，{An}n∈N，{Cn}n∈N)是势博弈。

定义势函数为：

其中：I{condition}是指示函数，条件为真则I{condition}=1，否则I{condition}=0。

定理1如果通过构造势函数将成本开销最小化问题转化为势博弈，那么它在有限的改进内拥有至少一个纳什均衡。

证明 首先将成本开销最小化问题转化为策略博弈。假设移动设备n要更新当前策略an，并且存在决策使得Cn(，a-n)＜Cn(an，a-n)成立。根据势博弈的定义，需要表明成本开销减少的同时，势函数也会变小，即P(a-n)＜P(an，a-n)。考虑下列3种情况：1）an＞0，＞0；2）an＞0，=0；3）an=0，＞0。

1）假设当前移动设备n的策略是an＞0，更新其为＞0，即Cn(，a-n) ＜Cn(an，a-n)。那么有：

此时可得P(an，a-n) -P(，a-n) ＞0。

2）假设当前移动设备n的策略是an＞0，更新其为=0，那么有：

由于an＞0 且=0，说明THn，所以有P(an，a-n) -P(，a-n) ＞0。

3）假设当前移动设备n的策略是an=0，更新其为此时有因此可以得到

综合以上三种情况可得，策略的改变所造成的成本开销的减少会导致势函数的减少。通过构造势函数P(a)可知博弈G是一个势博弈，证明的关键在于移动设备n改变其当前的策略an为更好的策略，使开销成本减小的同时导致任务迁移博弈的势函数变小。根据定理1 可得，对每个具有有限策略空间的势博弈，都存在纳什均衡。这意味着任何更新参与者策略并改善其成本开销的算法都可以保证在有限时间内达到纳什均衡。

3 基于博弈论的两阶段任务迁移算法

本章设计基于博弈论的两阶段任务迁移算法（Game Theory-Two Stages Task Offloading，GT-TSTO）。在第一阶段移动设备决定任务本地执行还是迁移到MEC 服务器执行，第二阶段是迁移至MEC 之后要决定是MEC 继续执行还是迁移到CCC执行。

3.1 算法设计与描述

通过迭代更新移动设备n的最佳响应策略，在每一次迭代的过程中，移动设备n通过计算求得使成本开销最小的策略作为最佳响应策略，从而来响应其他移动设备的策略。MEC 服务器可以计算出传输速率，并传送给移动设备。由定义2 可知，如果最佳响应算法是收敛的，那么所有移动设备最佳响应策略的固定点集是博弈G的纳什均衡；但是收敛时间是随着移动设备的数量呈指数增长的。为了能够获得结果令人满意的迁移决策，GT-TSTO算法被设计实现纳什均衡。

GT-TSTO 算法是一个分布式的任务迁移算法，系统的基站是可以时间同步的，可以通过基站时间来同步所有移动设备的操作。当移动设备想要更新决策时，它们向基站广播其参数。算法进行比较后允许其中一个开销成本最小的设备获得更新决策的机会。经过多次迭代后，所有移动设备的迁移决策达到稳定状态，此时达到开销最小化的纳什均衡。

在每一个准静态场景下的决策时隙内，每一个移动设备都会依据自己的策略是否更新来决定是否发送更新请求消息（Request Update，RU）。RU 表明每个移动设备都想竞争更新决策（Update，UP）的机会来改善当前决策。假设移动设备n赢得了决策机会，则n选择一个最佳响应决策作为更新决策，最小化自身的成本开销。在有限次的迭代后，所有的移动设备达到了相互平衡的状态，即纳什均衡。

具体地，GT-TSTO算法的运行过程有以下几个步骤。

1）无线干扰测量。移动设备可以从基站获得相关信道的信息，在每个给定的决策时隙t内计算当前的无线信道干扰和传输速率。对每一个的移动设备n，它们在自己选择的信道向无线基站发送信道信号，无线基站测量每个信道的总接收功率Pk(a(t))，这样移动设备n可以得到自身所收到的无线信道干扰。无线信道干扰可以通过公式计算：

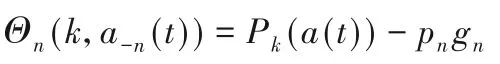
2）迁移决策更新。根据不同信道上测量出的信道干扰Θn(k，a-n(t))计算移动设备的最佳响应集其中

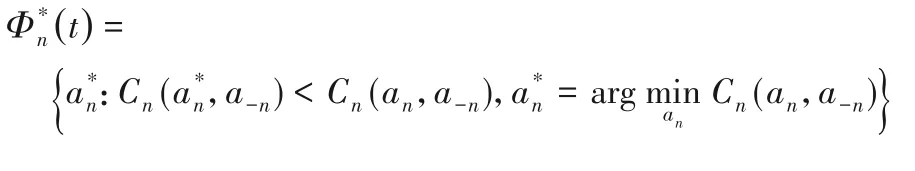
之后，GT-TSTO算法进入下一个循环，直到没有移动设备在下一个决策时隙中找到当前的最佳迁移决策，并且经过有限次的迭代后，所有移动设备都将达到纳什均衡的状态，循环才会结束。最后可以根据所有移动设备的最终迁移决策列表计算出最小的总能耗。

具体算法描述如下：

算法1 基于博弈论的两阶段任务迁移算法（GT-TSTO）。

输入 移动设备n的计算任务an，传输功率pn以及其他初始数据。

输出 移动设备最优决策集Sa、Sy和系统总成本开销Ctotal。

初始化 设置初始决策槽t=0；移动设备n的决策结果an(0)=0。

根据势博弈的有限改进属性，本算法可以在有限次的迭代决策后收敛到纳什均衡。在仿真实验中，在MEC 服务器未接收到RU 消息时可以终止任务迁移决策更新过程。这时MEC 服务器向所有移动设备广播终止信息，并且每一个移动设备根据最后的决策时隙内所获得的决策来执行任务。

在每个决策时隙内，移动设备会并行执行算法1中的2）～14）行的操作。尽管GT-TSTO 算法只能为云边协作下的任务迁移提供近乎最优的解决方案，但由于是随机选取移动设备更新决策，这会使得算法拥有更高的计算效率。本算法主要涉及K个无线信道测量数据的排序操作，所以每一个决策时隙内的计算复杂度为O(KlgK)，假设算法达到纳什均衡需要I次迭代，那么本文的分布式任务迁移算法的总计算复杂度为O(IKlgK)。

3.2 性能分析

GT-TSTO算法性能通过研究策略博弈的重要性能指标来分析——纳什均衡的整体性能和最优配置相差多少？通过PoA（Price of Anarchy）来量化这种差异，它反映了自私个体基于自身利益自由选择策略对整体利益的影响程度，PoA 值的大小可以用来衡量纳什均衡的性能。PoA 定义为在纳什均衡中获得的最差社会成本和全局最优策略方案所获得的最小社会成本之间的比率。

社会成本被定义为所有移动设备的总成本开销，即：

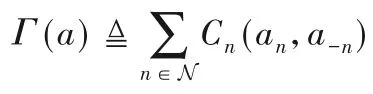
PoA可以被定义为：

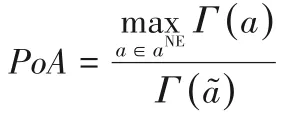
无线通道数量增加，可以减少来自干扰用户的干扰，PoA减小，这表明减少干扰时可以提高NE的性能。而当移动设备本地成本较低时，最差的纳什均衡接近于集中式最优解决方案，此时的PoA也较低。

4 实验仿真

为了评估所提的云边协同任务迁移方案的性能，本章将展示通过仿真实验所产生的数值结果。在不失一般性的情况下，本文采用光纤无线混合网络下集中式云服务器和MEC 协同方案。

假设每个MEC具有30个正交信道频率资源，这意味着它最多可以同时服务30 个移动设备，并且其信道带宽设置为5 MHz，每个基站信道数为5，同时在MEC 的覆盖范围内随机分配15～50 个移动设备。此外，移动设备的传输功率设置为2 W，背景噪声设置为-80 dBm，信道增益取值为0.7～0.9，计算的数据大小为｛500，1 000，1 500，2 000｝KB，第二阶段所需等待时间设置为0.1～2 s，任务所需的CPU 周期数随机分布为｛1 000，2 000，3 000，4 000｝Mega cycles，MEC 和CCC 的计算能力分别为10 GHz和20 GHz，移动设备的计算能力随机分布为｛0.5，0.8，1.0｝GHz。MEC 与CCC 的数据传输率为15 Mb/s，能量负载因子随机分布于｛0，0.2，0.5，0.8，1.0｝，相应的时间负载因子为1-

图1 展示了有益任务迁移状态的移动设备数动态变化的过程。从图1 可见，随着迭代次数增加，移动设备根据信道信息不断调整任务迁移策略，使得处于有益迁移状态的移动设备数也在增加，并最终达到稳定状态，说明GT-TSTO 算法可以在有限次数的迭代内达到纳什均衡。

图1 有益任务迁移状态的移动设备数变化Fig.1 Change of the number of mobile devices with beneficial task offloading status

图2 展示了多个移动设备在本文所提的云边环境下基于非合作博弈的任务迁移成本开销变化情况，每一条折线代表一个移动设备从初始到达到纳什均衡的成本开销实时变化曲线。由于本仿真中MEC可以最多同时服务30个移动设备，所以初始设置了30个移动设备同时进行任务迁移。

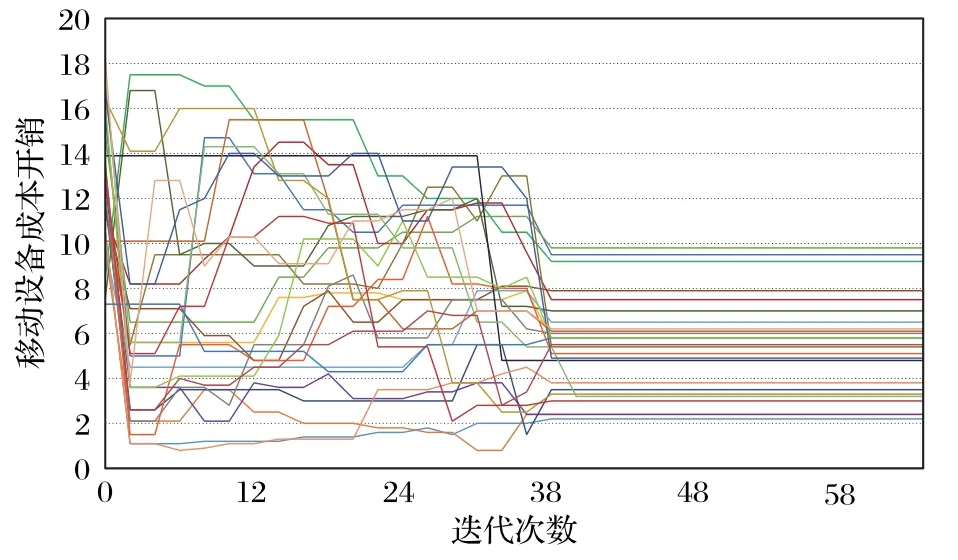
图2 不同移动设备的成本开销Fig.2 Overhead of different mobile devices

从图2 可以看出每个移动设备的开销随着迭代次数的增加而变化，最终趋于稳定，这说明此时已达到纳什均衡，而且对于单个移动设备来说，迭代过程中迁移决策是不断变化的，这是移动设备作为博弈方所进行的迁移决策调整。因此在达到纳什均衡之前，移动设备的成本开销是不规则变化的，达到纳什均衡后开销保持恒定，但不同移动设备间的成本开销是不同的。此时可以证明博弈G是收敛的，纳什均衡存在且唯一。从图2 可得出结论，与初始值相比，纳什均衡下的移动设备总开销减少了，这表明云边环境下基于博弈论的任务迁移方法是可以有效减少开销的。

图3 是不同数量的移动设备达到纳什均衡所需的迭代次数。随着移动设备数的增加，达到纳什均衡需要的迭代次数也线性增加，这说明本文所提出的云边环境下的GT-TSTO 算法有较好的性能。

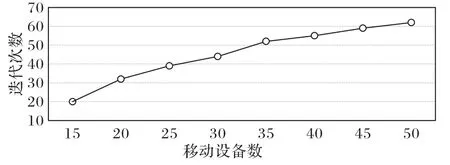
图3 不同数量移动设备达到纳什均衡的迭代次数Fig.3 Number of iterations for different numbers of mobile devices to reach Nash equilibrium

图4 将GT-TSTO 算法在不同移动设备数的情况下获得的最小总成本开销，与本地计算、无排队等待的MEC 计算和中心云计算进行对比。所有移动设备的总成本开销都会随着移动设备数的增加而增加，但与本地计算与云计算相比，MEC计算和云边协作计算都可以实现更少的成本开销，而云边协作计算性能更好，这验证了GT-TSTO 算法能够有效减少总成本开销。当移动设备数为30 时，所提算法所产生的总开销为147，而本地执行、云中心服务器执行和MEC 执行的移动设备总成本开销分别为540、281和151，因此可以得到云边环境下进行任务迁移分别比本地执行、云中心服务器执行和MEC 服务器执行降低了72.8%、47.9%和2.65%。由于MEC 的可用计算资源不足以满足那些需要较多计算资源的任务，以上这些结果验证了在MEC 环境中引入集中式云计算进行任务迁移的必要性。

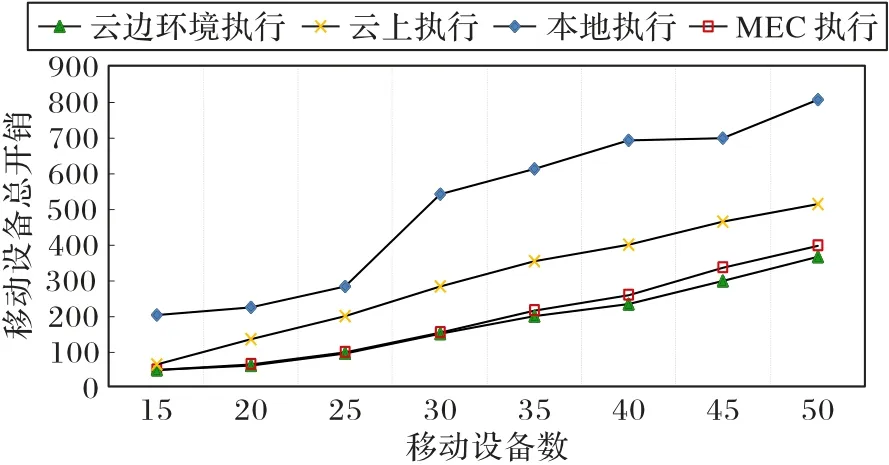
图4 采用不同的任务迁移方案的总开销的比较Fig.4 Comparison of total overhead using different task offloading schemes

5 结语

本文研究了云边协作任务迁移问题，以最大限度降低迁移开销为优化目标，提出了在云边协作环境下基于博弈论的两阶段任务迁移方案，以获得最佳迁移策略。通过本算法可以有效降低成本开销，产生成本效益，而且能够实现更低的能耗。但本文研究仍存在不足，目前仅考虑单MEC 服务器与云服务器协同，而未考虑到多MEC 服务器与云服务器协同的复杂任务迁移情况。今后会深入研究多MEC 服务器与云服务器协作任务迁移，进一步降低能耗，减少任务迁移的成本开销。