温度和车速对半刚性基层沥青路面模量场和疲劳寿命的影响
黄立葵 宋伟 姜正晖 杨树

摘 要:为分析半刚性基层沥青路面中沥青层模量在时间域和空间域上的分布特征,研究模量场年变化对结构层疲劳寿命的影响,将沥青面层细分为1 cm厚的亚层,基于Odemark法经迭代计算得到了沥青层中的模量场分布,分析全年456种工况下路面结构的力学响应,基于Miner线性疲劳损伤模型计算得到了考虑模量场影响的疲劳寿命修正系数. 结果表明:模量场随时间显著变化,车速为70 km/h时,沥青层各深度处的模量年最大与最小值之比达20.1~34.9,且同一时间沿路面深度方向的模量不相等;车速对模量场有显著影响,车速120 km/h与10 km/h时,沥青层模量之比达1.12~2.28;路面结构的疲劳寿命分析中,应考虑模量场年变化的影响,在20 ℃、10 Hz标准工况下分析得到的上基层疲劳寿命偏保守,下基层疲劳寿命偏危险,建议采用考虑模量场影响的疲劳寿命修正系数调整标准工况下计算得到的结构层疲劳寿命.
关键词:道路工程;沥青路面;模量场;疲劳寿命;修正系数
中图分类号:U416 文獻标志码:A
Abstract:In order to analyze the distribution characteristics of the modulus field of semi-rigid asphalt pavement in the time domain and spatial domain and to study the effect of the annual change of the modulus field on the fatigue life of the structural layers, the asphalt layers were subdivided into several sub-layers with a thickness of 1 cm. The modulus field distribution in the asphalt layers was obtained by iterative calculations based on the Odemark method, and the fatigue life correction factors of structural layers were obtained based on the Miner linear fatigue damage model as well as the mechanical responses of the pavement structure under 456 conditions throughout the year. The results show that the modulus field varies significantly with time. At the speed of 70 km/h, the ratio of the annual maximum and minimum values of the modulus at each depth of the asphalt layer reaches 20.1~34.9, and the modulus with the pavement depths are not equal at the same time. The ratio of the modulus at the speed of 120km/h to that at 10 km/h is in the range of 1.12 ~ 2.28, which means that the vehicle speed has a significant effect on the modulus field. The influence of the annual change of the modulus field on the fatigue life of pavement structures should be considered. The fatigue life of the upper base calculated under the standard conditions at 20 ℃ and 10 Hz is conservative, while the fatigue life of the lower base is dangerous. The calculation results under the standard condition should be revised by the fatigue life correction factor when checking the fatigue life of the pavement structures.
Key words:road engineering;asphalt pavement;modulus field;fatigue life;correction factor
为获得交通荷载作用下路面结构的真实力学响应,必须合理地选用路面材料的计算参数. 作为一种典型的黏弹性材料,沥青混合料的模量显著依赖于温度和荷载作用频率. 受外界环境的影响,路面结构内部的温度场变化显著,而路面温度场变化必将导致沥青材料层沿路面深度方向的模量分布随之变化. 此外,不同的行车速度对应不同的荷载作用时间,即使在相同的行车速度下,路面不同深度处的应力脉冲持续时间也存在较大差异,这等效于不同深度处的加载频率不同. 因此,在确定路面材料计算参数时,必须考虑沥青层模量的温度和车速依赖性.
在有关路面力学响应的研究和我国现行路面设计规范中[1-9],大多将路面同一结构层的材料参数视为一致,这与真实情况相差很大,基于此计算得到的路面力学响应自然也不够准确. 对于沥青路面,荷载、环境、路面结构组成一个不可分离的系统,在荷载、环境的综合作用下,沥青材料层模量以“场”的形式分布. 为了更合理地分析路面结构的力学响应,本文首先对长沙地区沥青路面的模量场在时间域和空间域的分布特征展开研究,并分析了车速对模量场的影响. 在此基础上,以模量场计算结果作为路面力学响应计算的材料输入参数,分析了模量场变化下半刚性基层沥青路面的疲劳寿命,并以标准工况下路面结构的疲劳寿命为基准,计算得到了各工况下考虑模量场影响的疲劳寿命修正系数.
1 模量场计算方法
1.1 路面温度场
路面温度场受多种因素共同影响,其中气温和太阳辐射是最主要的影响因素,其他因素的影响可以通过气温和太阳辐射体现出来[10-11]. 孙立军等[11]在我国多个地区进行了大量实测,建立了式(1)所示的考虑地区差异的路面温度场预估模型,可采用此模型计算路面不同时刻的温度场.
1.2 路面应力脉冲持续时间
Barksdale[13]、Brown[14]、Hu等[15]均提出了行车荷载下,路面结构中应力脉冲持续时间的计算方法,Odemark最早提出了等效厚度的概念,在美国最新版MEPDG中得到了应用[16],本文采用基于等效厚度的Odemark法计算路面结构中的应力脉冲持续时间.
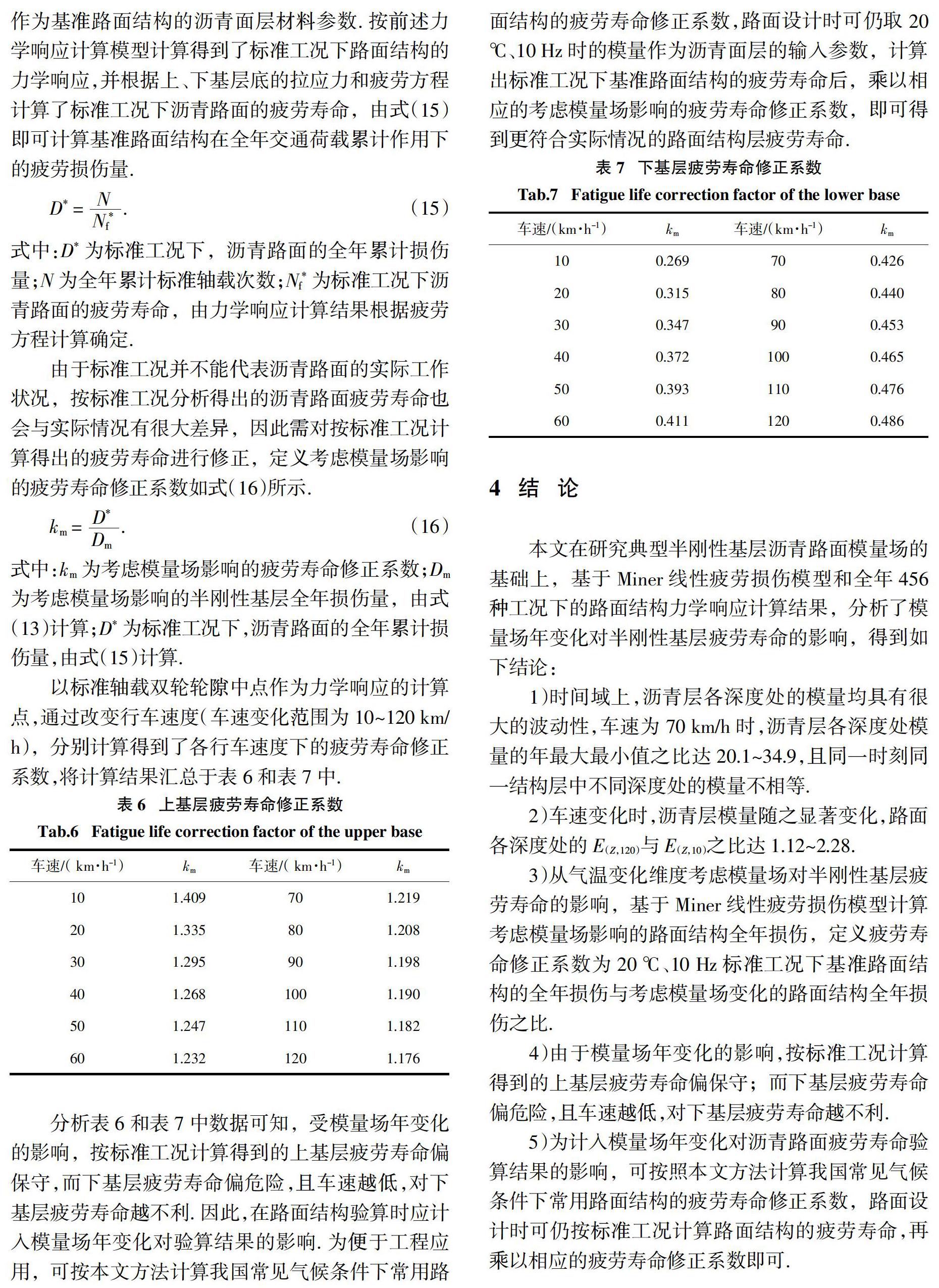
通过式(5)将路面各结构层换算为与路基模量相同的等效层,并在换算后的等效路面结构中按45°的扩散角向下传递交通荷载,据此可经迭代计算得到路面结构中任一深度处的应力影响长度Leff,应力影响长度的概念见图1,该深度处的荷载作用时间由式(6)计算.
式中:he为待换算层的换算厚度,m;h1为换算层的实际厚度,m;E1为换算层的模量,MPa;μ1为换算层的泊松比;E2为路基的模量,MPa;μ2为路基的泊松比;t为应力脉冲持续时间,s;Leff为计算深度处的应力影响长度,m;v为行车速度,m/s.
1.3 路面模量场
路面结构不同深度处的温度和荷载作用频率不同,受其影响,沥青层不同深度处的模量也并不一致,为客观反映沥青层的模量沿路面深度方向的分布情况,应将其模量视为“场”,即“模量场”.
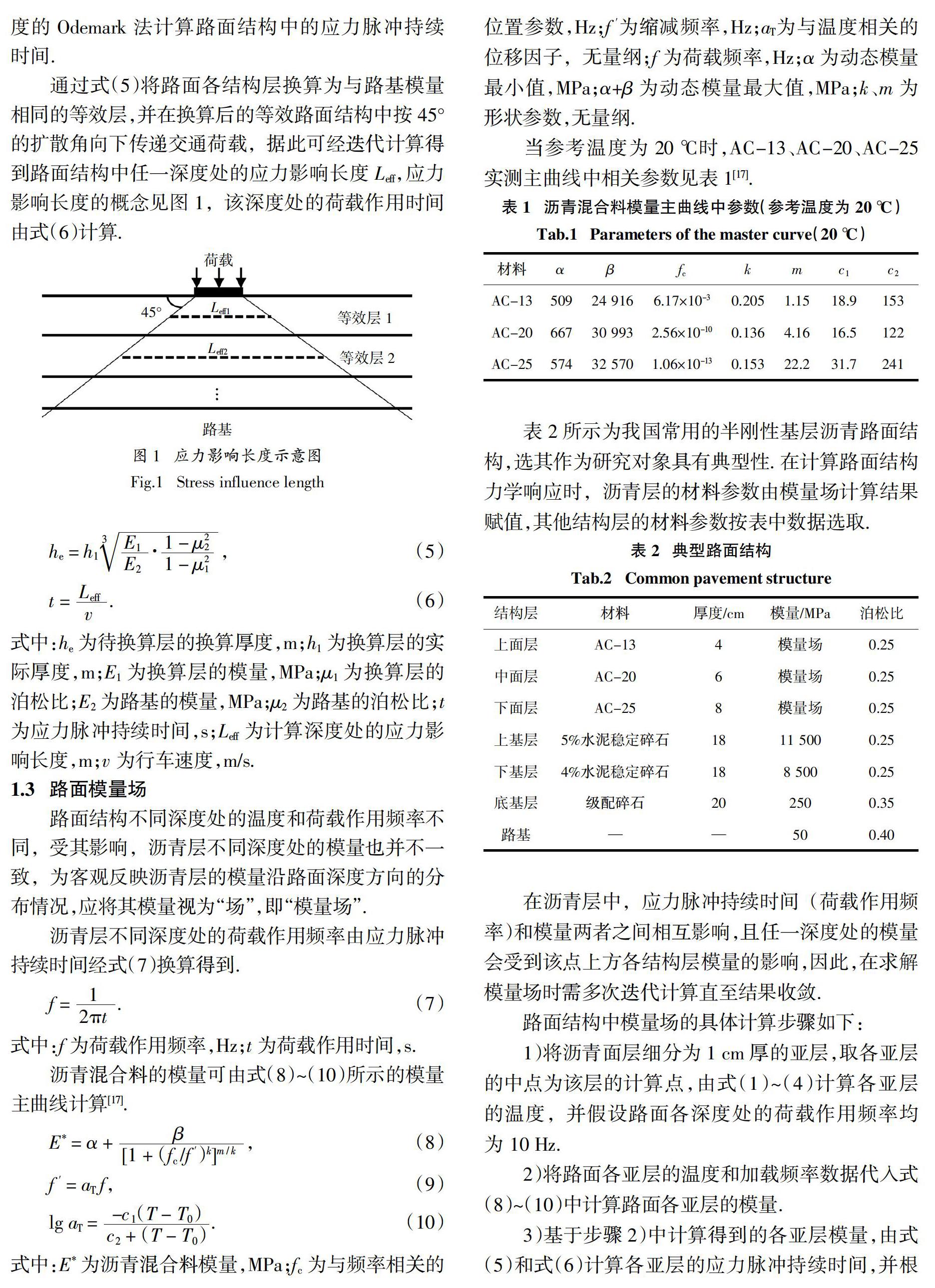
表2所示为我国常用的半刚性基层沥青路面结构,选其作为研究对象具有典型性. 在计算路面结构力学响应时,沥青层的材料参数由模量场计算结果赋值,其他结构层的材料参数按表中数据选取.
在沥青层中,应力脉冲持续时间(荷载作用频率)和模量两者之间相互影响,且任一深度处的模量会受到该点上方各结构层模量的影响,因此,在求解模量场时需多次迭代计算直至结果收敛.
路面结构中模量场的具体计算步骤如下:
1)将沥青面层细分为1 cm厚的亚层,取各亚层的中点为该层的计算点,由式(1)~(4)计算各亚层的温度,并假设路面各深度处的荷载作用频率均为10 Hz.
2)将路面各亚层的温度和加载频率数据代入式(8)~(10)中计算路面各亚层的模量.
3)基于步骤2)中计算得到的各亚层模量,由式(5)和式(6)计算各亚层的应力脉冲持续时间,并根据计算结果由式(7)计算各亚层的荷载作用频率.
4)基于步骤3)中计算得到的荷载作用频率数据,按步骤2)重新计算路面各亚层的模量.
重复步骤2)~4),直至各亚层的模量在前后两次计算结果中的差值小于1 MPa. 鉴于迭代计算过程繁琐,编写了相关程序,借助计算机自动完成迭代求解过程.
2 模量场计算结果
如前所述,将沥青面层细分为1 cm厚的若干亚层,取每个亚层的中点为该层的计算点,基于一整年的气象数据,以1 h为时间间隔,并考虑车速的影响,通过迭代计算得到了全年各工况下沥青路面结构层逐小时模量场分布. 我国高速公路上行驶的重载货车的车速大多为60~80 km/h,不失一般性,当分析模量场在时间域和空间域上的分布特征时,取基准车速为70 km/h.
2.1 模量场时间域分布特征
沥青结构层的模量场与外界环境紧密相关,在时间域上的波动性很大. 以E(z,v)表示车速v(km/h)时路面深度Z处的沥青层模量. 图2所示为路面不同深度处E (Z,70)的全年逐小时变化情况,1.5 cm、6.5 cm、13.5 cm、17.5 cm深度处的模量年最大值分别为20 224 MPa、23 246 MPa、23 865 MPa、24 982 MPa,年最小值分别为607 MPa、1 151 MPa、698 MPa、778 MPa,最大最小值之比分别达到33.3、20.2、34.2、32.1. 进一步分析了沥青层其他深度处的模量年最大最小值之比,数据分析结果表明在70 km/h车速时,沥青层各深度处的模量年最大最小值之比均位于20.1~34.9. 由此可见沥青层各深度处的模量在全年的变化范围均很大.
根据我国现行《公路沥青路面设计规范》(JTG D50—2017),在分析路面結构的力学响应时,将20 ℃、10 Hz时的沥青混合料模量作为沥青面层的输入参数,由式(8)~(10)计算可得20 ℃、10 Hz时AC-13、AC-20、AC-25的模量分别为8 683 MPa、11 090 MPa、11 950 MPa,但这种材料参数取值方法并不能反映沥青混合料的模量随时间变化的情况. 为直观反映沥青层各深度处的模量随时间的波动性,以1 000 MPa为模量区间,统计分析了全年8 760 h中路面各深度处的模量在各模量区间出现的小时数,并将其与全年8760 h的比值汇总于表3中. 分析表3中数据可知,在路面0~4 cm深度范围内(即AC-13结构层中),1.5 cm深度处的模量在全年8 760 h中处于8 000~9 000 MPa范围内的小时数最多,但也只有456 h,仅占全年时间的5.21%;路面4~10 cm深度范围内(即AC-20结构层中),7.5 cm深度处的模量在全年8 760 h中处于11 000~12 000 MPa范围内的小时数最多,但也只有363 h,仅占全年时间的4.14%;路面10~18 cm深度范围内(即AC-25结构层中),17.5 cm深度处的模量在全年8 760 h中处于11 000~12 000 MPa范围内的小时数最多,但也只有397 h,仅占全年时间的4.53%. 由此可见,现行《公路沥青路面设计规范》(JTG D50—2017)中有关沥青混合料材料参数的取值方法并不能够反映材料在实际工程中的情况. 因此,为保证计算结果的准确性,在进行路面结构验算时,必须考虑沥青层模量在时间域上的波动性对验算结果的影响.
2.2 模量场空间域分布特征
分别选取1月、4月、7月和10月作为冬、春、夏、秋季的代表月,并在每个代表月中选取日平均气温与月平均气温最为接近的一天作为该月的代表日. 图3所示为车速70 km/h时1月28日、4月1日、7月19日和10月22日代表性时刻的路面模量场分布. 分析图3可知,在各结构层的分层处,由于材料不同,模量具有显著差异. 即使在同一结构层中,沥青混合料的模量也会沿路面深度发生变化,如1月28日0:00,AC-13、AC-20、AC-25结构层中模量最大最小值之差分别为844 MPa、1 565 MPa、831 MPa,这自然也会影响路面结构的力学响应分析结果,因此在验算路面结构的疲劳寿命时还应考虑沥青层模量沿路面深度方向的分布情况,不应简单地将同一结构层不同深度处的模量视为定值.
2.3 沥青层模量的速度依赖性
实际道路上行驶的车辆车速变化范围很大,不同的行车速度对应路面结构不同的荷载作用时间,等效于荷载的加载频率不同,进而对沥青层各深度处的模量值和整个沥青层中的模量场分布产生影响.
图4、图5分别为10月22日10:00沥青层不同深度处的模量随车速的变化情况. 数据分析表明:随着车速的提高,各深度处的模量值均显著增大,如当车速从10 km/h提高至120 km/h时,0.5cm深度处E (0.5,120)与E (0.5,10)之比达1.89,17.5 cm深度处E (17.5,120)与E (17.5,10)之比达1.72. 进一步分析发现沥青层各深度处的模量在全年中任意时刻E (Z,120)与E (Z,10)之比均位于1.12~2.28,表明车速对沥青路面的模量场具有显著影响. 但在现行的 《公路沥青路面设计规范》(JTG D50—2017)中,材料参数取为定值,这并不能反映不同车速时沥青层模量的差异性,因此在路面结构验算中还应考虑车速的影响.
3 模量场在路面结构疲劳寿命验算中的应用
不同的模量场分布特征下,路面结构的疲劳寿命具有显著差异,因此在路面结构的疲劳寿命验算中必须计入模量场的影响. 根据我国现行沥青路面设计规范,验算路面结构的疲劳寿命时,将20 ℃、10 Hz时的模量作为沥青面层的输入参数,由前述分析可知,这不能反映真实情况,以此为基础的计算结果自然也与实际状况相差很大,因此很有必要在模量场计算结果的基础上,对沥青路面的疲劳寿命计算结果进行修正.
受外界环境因素的影响,一年中沥青路面的模量场变化很大,需综合分析全年中不同工况下,模量场对路面结构疲劳寿命的影响. 为此,在全年气温变化范围内以1 ℃为步长,将气温划分为若干个区段,在每个温度区间内选择一个代表时刻,将该时刻各行车速度下的模量场作为结构验算时沥青面层的材料输入参数,并基于路面结构层的力学响应计算结果和对应的疲劳方程计算对应工况下的路面结构疲劳寿命.
计算各工况下沥青路面结构的力学响应时,使用ABAQUS软件建立了横向、纵向、竖向尺寸分别为8 m、8 m、6 m的路面结构有限元模型,采用C3D8单元将模型划分为24万个单元,模型底部和四周限制法向位移,假定各结构层间完全连续. 为考虑模量场的影响,在模型中将沥青面层细分为1 cm厚的亚层,每一亚层的材料参数根据模量场计算结果取值.
一天中不同时间段内交通量不同,因此在统计每个温度区间的交通量时,需对每个时间段分别统计,表4所列为湖南省内某高速公路1 d中各时段内的交通量分布情况[18],在表4的基础上按以下步骤统计各温度区间的全年交通量:
1)将全年每一天的24 h按1 h的时间跨度划分为24个区间,并假设每个时间段的交通量不随日期变化,因此可将全年中每个时间区间的总计365 h划入同一个统计时段.
2)统计全年8 760 h的逐小时气温数据,统计结果表明长沙全年气温变化范围为-7~+39 ℃,按1 ℃为温度跨度将气温划分为若干个温度区间.
3)不同日期的同一时刻气温不同,基于1)中的假设,在每个统计时段的365 h中,处于各温度区间的交通量占该统计时段365 h的总交通量的比例与所处该温度区间的小时数占365 h的比例相同,据此可计算某统计时段位于某一温度区间的交通量.
4)将不同时间段内同一温度区间的交通量相加,即可得到全年中该温度区间的累计交通量.
分析表6和表7中数据可知,受模量场年变化的影响,按标准工况计算得到的上基层疲劳寿命偏保守,而下基层疲劳寿命偏危险,且车速越低,对下基层疲劳寿命越不利. 因此,在路面结构验算时应计入模量场年变化对验算结果的影响. 为便于工程应用,可按本文方法计算我国常见气候条件下常用路面结构的疲劳寿命修正系数,路面设计时可仍取20 ℃、10 Hz时的模量作为沥青面层的输入参数,计算出标准工况下基准路面结构的疲劳寿命后,乘以相应的考虑模量场影响的疲劳寿命修正系数,即可得到更符合实际情况的路面结构层疲劳寿命.
4 结 论
本文在研究典型半刚性基层沥青路面模量场的基础上,基于Miner线性疲劳损伤模型和全年456种工况下的路面结构力学响应计算结果,分析了模量场年变化对半刚性基层疲劳寿命的影响,得到如下结论:
1)时间域上,沥青层各深度处的模量均具有很大的波动性,車速为70 km/h时,沥青层各深度处模量的年最大最小值之比达20.1~34.9,且同一时刻同一结构层中不同深度处的模量不相等.
2)车速变化时,沥青层模量随之显著变化,路面各深度处的E (Z,120)与E (Z,10)之比达1.12~2.28.
3)从气温变化维度考虑模量场对半刚性基层疲劳寿命的影响,基于Miner线性疲劳损伤模型计算考虑模量场影响的路面结构全年损伤,定义疲劳寿命修正系数为20 ℃、10 Hz标准工况下基准路面结构的全年损伤与考虑模量场变化的路面结构全年损伤之比.
4)由于模量场年变化的影响,按标准工况计算得到的上基层疲劳寿命偏保守;而下基层疲劳寿命偏危险,且车速越低,对下基层疲劳寿命越不利.
5)为计入模量场年变化对沥青路面疲劳寿命验算结果的影响,可按照本文方法计算我国常见气候条件下常用路面结构的疲劳寿命修正系数,路面设计时可仍按标准工况计算路面结构的疲劳寿命,再乘以相应的疲劳寿命修正系数即可.
参考文献
[1] YOU L Y,YAN K Z,HU Y B,et al. Spectral element method for dynamic response of transversely isotropic asphalt pavement under impact load[J]. Road Materials and Pavement Design,2018,19(1):223—238.
[2] 董泽蛟,潘小康,邵显智,等. 温度场及非均布移动荷载作用下沥青路面力学响应分析[J]. 同济大学学报(自然科学版),2016,44(5):740—746.
DONG Z J,PAN X K,SHAO X Z,et al. Dynamic response analysis of asphalt pavement due to combined non-uniform moving load and temperature distribution[J]. Journal of Tongji University(Natural Science),2016,44(5):740—746. (In Chinese)
[3] 刘能源,颜可珍,胡迎斌,等. 基于横观各向同性的沥青路面加铺层力学分析[J]. 湖南大学学报(自然科学版),2017,44(5):96—103.
LIU N Y,YAN K Z,HU Y B,et al. Mechanical analysis of asphalt concrete overlay over old asphalt pavements considering cross-anisotropy properties[J]. Journal of Hunan University(Natural Sciences),2017,44(5):96—103. (In Chinese)
[4] 萬晨光,申爱琴,薛翠真,等. 层间接触状态对桥面铺装结构力学响应的影响[J]. 湖南大学学报(自然科学版),2016,43(9):113—119.
WAN C G,SHEN A Q,XUE C Z,et al. Effcet of interlayer contact state on mechanical response of bridge deck pavement structure[J]. Journal of Hunan University (Natural Sciences),2016,43(9):113—119. (In Chinese)
[5] 郭寅川,王礼根,申爱琴,等. 动载作用下级配碎石基层沥青路面力学分析[J]. 公路交通科技,2016,33(1):27—33.
GUO Y C,WANG L G,SHEN A Q,et al. Dynamic analysis of graded crushed stone as base of asphalt pavement[J]. Journal of Highway and Transportation Research and Development,2016,33(1):27—33. (In Chinese)
[6] SUN Y Z,GUO R,GAO L,et al. Study on dynamic response characteristics of saturated asphalt pavement under multi-field coupling[J]. Materials,2019,12(6):959.1—959.15.
[7] 刘大维,戴宗宏,陈洋,等. 车辆多轮动载作用下柔性路面动应力响应[J]. 中国公路学报,2017,30(11):36—44.
LIU D W,DAI Z H,CHEN Y,et al. Dynamic stress response of flexible pavement under multiple wheel dynamic loads of vehicle[J]. China Journal of Highway and Transport,2017,30(11):36—44. (In Chinese)
[8] XIA R X,LI J H,HE J,et al. Effect analysis of vehicle system parameters on dynamic response of pavement[J]. Mathematical Problems in Engineering,2015,2015:1—8.
[9] 公路沥青路面设计规范:JTG D50—2017[S]. 北京:人民交通出版社,2017:12—20.
Specifications for design of highway asphalt pavement:JTG D50—2017[S]. Beijing:China Communications Press,2017:12—20. (In Chinese)
[10] 宋小金,樊亮. 沥青路面结构温度随深度变化规律研究[J]. 土木工程学报,2017,50(9):110—117.
SONG X J,FAN L. Study on the variation rules of temperature with depth for asphalt pavement structure[J]. China Civil Engineering Journal,2017,50(9):110—117. (In Chinese)
[11] 孙立军,秦健. 沥青路面温度场的预估模型[J]. 同济大学学报(自然科学版),2006,34(4):480—483.
SUN L J,QIN J. Prediction model on temperature field in asphalt pavement[J]. Journal of Tongji University(Natural Science),2006,34(4):480—483. (In Chinese)
[12] 曹其梦,于瑛,杨柳. 太阳逐时总辐射计算模型适用性分析:以我国部分地区为例[J]. 太阳能学报,2018,39(4):917—924.
CAO Q M,YU Y,YANG L. Applicability analysis of hourly total solar radiation calculation model-taking some regions of China as example[J]. Acta Energiae Solaris Sinica,2018,39(4):917—924. (In Chinese)
[13] BARKSDALE R D. Compressive stress pulse times in flexible pavements for use in dynamic testing[J]. Highway Research Record,1971,345(4):32—44.
[14] BROWN S F. Determination of youngs modulus for bituminous materials in pavement design[J]. Highway Research Record,1973,431:38—49.
[15] HU X D,ZHOU F J,HU S,et al. Proposed loading waveforms and loading time equations for mechanistic-empirical pavement design and analysis[J]. Journal of Transportation Engineering,2010,136(6):518—527.
[16] Applied Research Associates. Guide for mechanistic-empirical pavement design:NCHRP project 1-37A[R]. Washington DC:Transportation Research Board,2004:2—7.
[17] 宋小金,曾夢澜,樊亮. 沥青路面反算模量与沥青混合料动态模量的关系[J]. 土木工程学报,2019,52(4):121—128.
SONG X J,ZENG M L,FAN L. Relationship between back-calculated modulus of asphalt pavement and dynamic modulus of asphalt mixture[J]. China Civil Engineering Journal,2019,52(4):121—128. (In Chinese)
[18] 李喜,王选仓,房娜仁,等. 基于温度与荷载实际耦合的沥青路面车辙预估[J]. 长安大学学报(自然科学版),2018,38(5):67—75.
LI X,WANG X C,FANG N R,et al. Rutting prediction of asphalt pavement based on actual coupling of temperature and load[J]. Journal of Changan University (Natural Science Edition),2018,38(5):67—75. (In Chinese)

