长周期地震动的能量反应谱

李宇 李琛 赵福志 李钊

摘   要：选取139条长周期地震动记录作为输入，研究了恢复力模型参数（恢复力模型、刚度比η、阻尼比ξ、位移延性比μ）和地震动特性（周期T、震级MW、场地、PGA）对长周期地震的输入能量谱SEI、滞回耗能谱SEH和阻尼耗能谱SED的影响. 研究表明：1）恢复力模型对长周期（常规）地震能量谱的影响很大（小）;η对长周期和常规的地震动的能量谱的影响都很小;随着ξ增加，长周期（常规）地震的SEI的长周期段谱值增大（减小）;随着μ增加，长周期（常规）地震的SEH的峰值平台段延长（缩短）且峰值降低（增大）. 2）MW越大，结构损伤越大;场地土越软，能量谱值越大;若已知基准PGAref的能量谱，其他PGAoth的能量谱可由（PGAoth /PGAref）2调整得到. 基于以上的參数影响研究，采用三段式拟合函数，建立了长周期地震弹性输入能量设计谱，并拟合了μ和ξ对长周期地震能量谱的影响公式，进而得到长周期地震非弹性输入能量设计谱.

关键词：长周期地震动;输入能量谱;滞回耗能谱;阻尼耗能谱;设计谱

中图分类号：U448.27                            文献标志码：A

Abstract：A total of 139 long-period ground motion（GM） records are selected to study the effects of the parameters of restoring force models（restoring force models， stiffness ratio η，damping ratio ξ，displacement ductility ratio μ） and GM characteristics （period T，earthquake magnitude MW，site，PGA） on the input energy spectra SEI，hysteretic energy spectra SEH and damping energy spectra SED of the long-period GMs. Therefore， it can be found that： 1） there is a significant（slight） influence of the restoring force model on the long-period （conventional） seismic energy spectra， while there is a slight influence of the restoring force model on the conventional one; there is a slight influence of η on the long-period and conventional seismic energy spectra; with the increase of ξ，the spectral values in the long-period region of the long-period  SEI increases， but for the conventional one it decreases; with the increase of μ，the peak platform and peak value of the long-period SEH is prolonged and decreases， but for the conventional one they are shortened and increases，respectively. 2）the larger MW results in the greater structural damage，while the softer site soil leads to the larger energy spectra value;the seismic energy spectra with other PGAoth can be obtained by multiplying the known seismic energy spectra with the reference PGAref by the equation of （PGAoth /PGAref）2. Then，based on the above parametric studies，the elastic long-period input energy design spectra are established by using a three-segment fitting function， and the influence formulas of μ and ξ on the long-period spectra are fitted. And then the inelastic long-period input energy design spectra are obtained.

Key words：long-period ground motions（GM）;input energy spectra;hysteretic energy spectra;damping energy spectra;design spectra

2003年，在日本十胜冲地震中，苫小牧地区（震中距约225 km，PGA = 89.2 gal）的储油罐被破坏并引发火灾;北海道许多桥梁也发生破坏，如Rekifune Bridge跨中竖向位移达12 cm. 2011年，在东日本大地震中，东京都办公大楼（震中距约300 km）地下3层的最大加速度仅为74 gal，而顶部（48层）最大位移却达65 cm;大阪府办公大楼（震中距约700 km）顶部（52层）最大加速度仅为131 gal，而最大位移却达132 cm. 可见，长周期地震动（远场卓越周期偏大型地震动）对长周期结构有较大影响. 此后，学者们开始真正地关注长周期地震，并研究了长周期地震作用下的超高层建筑结构[1-5]、基础隔震结构[6-7]、隔震桥梁[8]、钢筋混凝土框架[9-10]和风电机组[11]等长周期结构的地震响应. 但是，上述研究仅停留在计算长周期结构地震响应的初步阶段，还未能在长周期地震作用下进行长周期结构的抗震设计. 究其原因，主要是由于缺乏抗震设计用的长周期地震反应谱.

目前，反应谱法仍是世界各国抗震规范中最主要的抗震设计方法，而反应谱则是该法的基础. 随着长周期结构的日益增多，我国《建筑抗震设计规范》（GB 50011—2010）[12]、《铁路工程抗震设计规范》（GB 50111—2006）[13]和《公路桥梁抗震设计规范》（JTGT 2231-01—2020）[14]分别将反应谱延伸至 6 s、5Tg和10 s，但仍未能满足工程应用要求，而且反应谱下降段也与实际长周期反应谱的特征不符（即特征周期Tg偏小、下降形式单一和幅值偏小）[15]. 因此，有必要针对长周期反应谱开展专门研究.

由于传统地震仪的缺陷和大震级地震发生的概率较小，记录到的长周期地震动时程并不多[15]. 因此，针对长周期地震动反应谱的研究还很少：张亮泉等[15]、李宇等[16]、Zhou等[17]对长周期地震的弹性、弹塑性加速度和位移反应谱等进行了初步探索;陈清军等[18]则选取了36条长周期地震动记录，对长周期地震的能量谱进行了研究. 但是，由于他们所依据的长周期地震动记录的数量太少，所得研究结果不具有统计意义，而且也没有详细讨论长周期地震的非弹性能量反应谱. 因此，本文通过对比长周期和常规地震动的特性，选取139条长周期地震动记录作为输入，以期建立长周期地震动的弹性和非弹性输入能量设计谱.

1   长周期地震动的特征

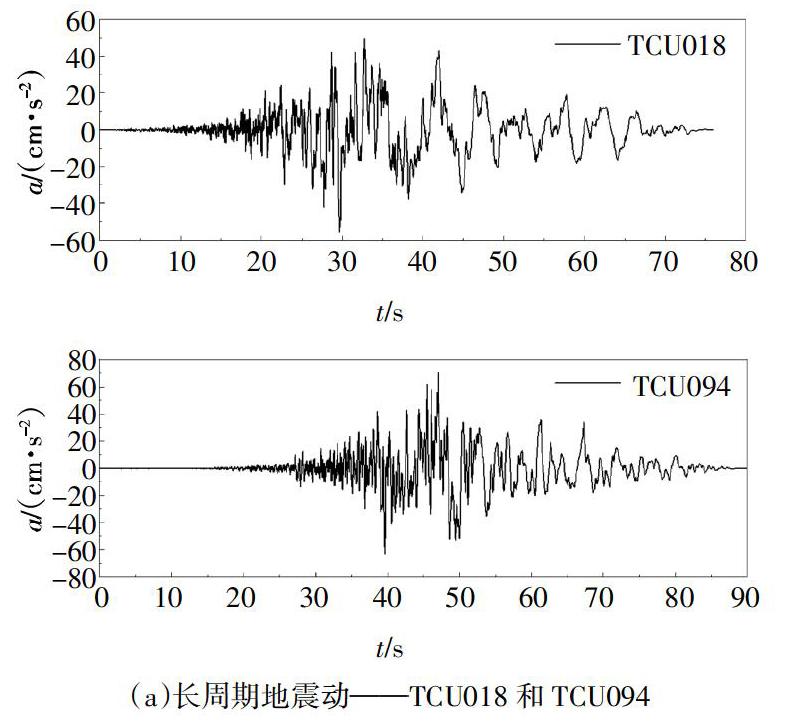
长周期地震动（台湾集集地震的TCU018和TCU094）和常规地震动（El Centro波和天津波）的加速度时程（t为时间，a为加速度）如图1所示. 通过傅里叶变换，可得其傅里叶幅值谱（如图2所示，f为频率，B为幅值），可知：常规地震动的卓越频率分布较宽，且集中在高频（1～5 Hz）;而长周期地震动的卓越频率分布较窄，且集中在低频（0.1～1.0 Hz）.

将4条地震动按同一PGA调幅后，对比它们的弹性加速度和位移反应谱（Sat为加速度谱值，D为位移谱值，T为周期），从图3可知：在长周期段，长周期地震动的谱值要远大于常规地震动，即长周期地震动对长周期结构（如大跨桥梁、超高层建筑）的影响很大.

2   长周期地震动的选取

根据长周期地震动记录的挑选标准[16-19]：震中距较大;卓越频率分布较窄，且集中在0.1～1.0 Hz的低频段;弹性加速度反应谱的峰值在中长周期段. 从PEER、K-NET和KIK-NET中挑选了139条长周期地震动记录（6级以上），并采用地震动数据处理软件SeismoSignal进行了滤波处理与基线校正，进而计算相关地震动参数.

根据文献[20]：美国抗震设计规范的vs30（覆盖层厚度为30 m的剪切波速） ≥ 510 m/s、260 m/s ≤ vs30 < 510 m/s、150 m/s ≤ vs30 < 260 m/s、vs30 < 150 m/s的场地分别对应中国抗震设计规范[12-14]的场地Site Ⅰ～Ⅳ.因此，可将139条长周期地震动记录按中国抗震设计规范[12-14]的场地标准进行分类，见表1：Site Ⅰ有38条，Site Ⅱ有40条，Site Ⅲ有41条，Site Ⅳ有20条.

再以139条长周期地震动记录作为激励，计算Ⅰ～Ⅳ类场地的动力放大系数β（阻尼比ξ=5%，周期为T），并与规范[14]的β曲线进行对比（见图4），从中可知：统计所得的β曲线与规范值符合较好. 可见，本文所选用的长周期地震动记录符合规范要求.

注意：当非弹性SDOF体系的m≠1时，以上各能量谱值应乘以m后，才能得到各类能量响应.

下文将考虑周期（T = 0.01～20 s）、恢复力模型、屈服后刚度比（η = k1/k2 = 0.0～0.05，k2为二次刚度）、位移延性比（μ = xmax /xy = l.0～5.0，xmax为最大位移，xy为屈服位移）、阻尼比（ξ = 2%～14%）、震级（MW）、场地、地震峰值加速度（PGA）的影响，利用BISPEC程序，研究长周期地震的非弹性能量谱（SEI、SEH、SED、SλH、SλD）.

3   恢复力模型参数的影响

3.1   恢复力模型

以Ⅱ类场地为例，将40条长周期地震动记录的PGA调幅为0.15g，采用考虑刚度退化的Takeda模型和无刚度退化的双线性模型（图5），并取η=0.05、ξ=5%、μ=1.0～5.0，采用BISPEC計算SEI、SEH、SED、SλD、SλH的平均值.

从图6可知，当μ相同时：1）无刚度退化模型的能量谱峰值平台段要长于刚度退化模型的能量谱峰值平台段，而且无刚度退化模型的特征周期也要大于刚度退化模型的特征周期;2）在中短周期段，无刚度退化模型的能量谱值要小于刚度退化模型的能量谱值，而在中长周期段则反之. 可见，相比于刚度退化模型，无刚度退化模型能量谱的峰值平台、特征周期和中长周期段谱值都要长或大，即采用无刚度退化模型的能量谱值对长周期结构进行抗震设计，会偏于保守.

从图7可知，当μ相同时，在中短周期段，2种模型的SλH和SλD的谱值差距较大，但随着T的增加，SλH和SλD的谱值逐渐趋于一致. 可见，长周期结构的周期越长，恢复力模型对塑性铰滞回耗能能力和系统阻尼耗能能力的影响就越小.

文献[23]研究了恢复力模型对常规地震能量谱的影响，与本文的研究结果对比后可知：

1）恢复力模型对常规地震能量谱的影响随着μ的增加而减小，特别是当μ>5 后，恢复力模型的影响可以忽略;但是，恢复力模型对长周期地震能量谱的影响则随着μ的增大而越加显著.

2）不同恢复力模型对应的常规地震能量谱的峰值平台段的长度和位置没有太大区别;但是，相比于双线性模型，Takeda模型的长周期地震能量谱的峰值平台段的长度更短而且更靠后（原点方向）.

3.2   屈服后刚度比

以I类场地为例，将38条长周期地震动记录的PGA调幅为0.15g，采用Takeda模型，取μ=1.0～5.0、ξ=5%，采用BISPEC计算η=0、0.025、0.05的SEI、SEH、SED、SλD、SλH的平均值.

从图8、图9可知：当μ相同时，η对SEI、SEH、SED、SλD、SλH的影响可以忽略，即在统计长周期地震能量反应谱时，可以不考虑η的影响.

文献[24]研究了η对常规地震能量谱的影响，从中可知：η对常规地震的能量谱谱值的影响很小. 这与η对长周期地震的能量谱的影响结论相同. 可见，无论是何种类型的地震动，η对地震能量谱的影响都是可以忽略的.

3.3   阻尼比

以I类场地为例，将38条长周期地震动记录的PGA调幅为0.15g，采用Takeda模型，取η=0.05，μ = l.0～5.0，采用BISPEC计算ξ=2%、5%、10%、14%时的SEI、SEH、SED、SλD、SλH的平均值.

从图10、图11可知：随着ξ增大，SEI峰值、SEH和SλH都逐渐减小，SEI长周期段谱值、SED和SλD都逐渐增大，而SEI峰值平台长度和特征周期则变化较小. 可见，ξ的增大，对SEI有削峰作用，并会增大SEI长周期段谱值，但不改变SEI峰值平台长度和特征周期;另外，随着ξ增大，塑性铰的滞回耗能能力降低，而系统的阻尼耗能能力提高.

文献[24]研究了ξ对常规地震能量谱的影响，与本文的研究结果对比后可知：ξ对常规地震和长周期地震的SEH和SED影响相同（随着ξ增大，不同类型地震的SEH减小而SED增大）;但是，ξ对不同类型地震的SEI长周期段的影响则不同（随着ξ增大，常规地震的SEI的长周期段的谱值减小，而长周期地震的SEI的长周期段的谱值则增大）.

3.4   位移延性比

以Ⅱ类场地为例，将40条长周期地震动记录的PGA调幅为0.30g，采用Takeda模型，取η=0.05、ξ=5%，采用BISPEC计算μ=1.0～5.0时的 SEI、SEH、SED、SλD、SλH的平均值.

从图12可知：随着μ的增大，SEI和SED的峰值减小，SEH峰值变化较小，SEI和SEH的峰值平台段增长，并往短周期方向移动，它们的特征周期也相应减小. 可见，μ的增大，对SEI和SED有削峰作用，并使SEI和SEH的峰值平台段往短周期方向移动，并减小它们的特征周期.

从图13可知，当其他条件相同时，在中短周期段，随着μ的增大，SλH增大而SλD则减小;但随着T的增加，SλH和SλD的谱值逐渐趋于一致. 可见，随着μ的增加，塑性铰的滞回耗能能力都提高，而系统的阻尼耗能能力则降低;另外，长周期结构的周期越长，μ对塑性铰滞回耗能能力和系统阻尼耗能能力的影响就越小.

文献[24]研究了μ对常规地震能量谱的影响，与本文的研究结果对比后可知：μ对常规地震和长周期地震的SEI和SED的影响规律相同（随着μ增大，SEI和SED都逐渐减小），但对与μ联系最紧密的SEH的影响规律则不同（随着μ增大，常规地震的SEH的峰值平台段后移（往原点方向））、平台段缩短、峰值增大，相反地，长周期地震的SEH的峰值平台段后移、平台段延长、峰值降低）.

4   地震动特性的影响

4.1   震级

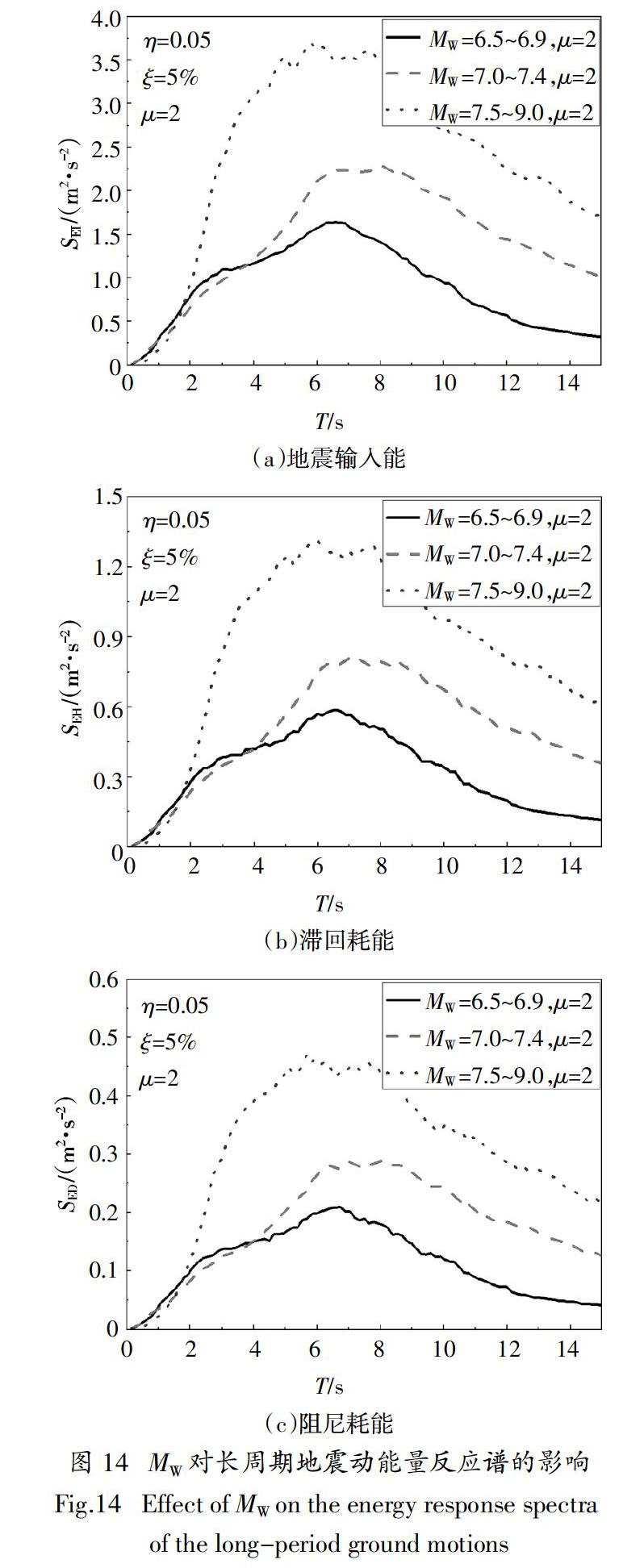
保持139条长周期地震动记录的原始PGA不变，并将它们按照MW = 6.5～6.9、7.0～7.4和7.5～9.0分组. 再采用Takeda模型，取η=0.05、ξ=5%、μ=2.0，用BISPEC计算SEI、SEH、SED、SλD、SλH的均值.

从图14可知，随着MW的增大，SEI、SEH、SED随之增大. 这是因为MW越大，地震释放的能量就越多，使得结构地震能量响应也越大.

从图15可知：随着MW的增大，SλH减小而SλD增大. 可见，MW越大，结构的损伤也就越大，塑性铰的滞回耗能能力下降，结构将主要依靠阻尼来消耗地震能量.

4.2   场地

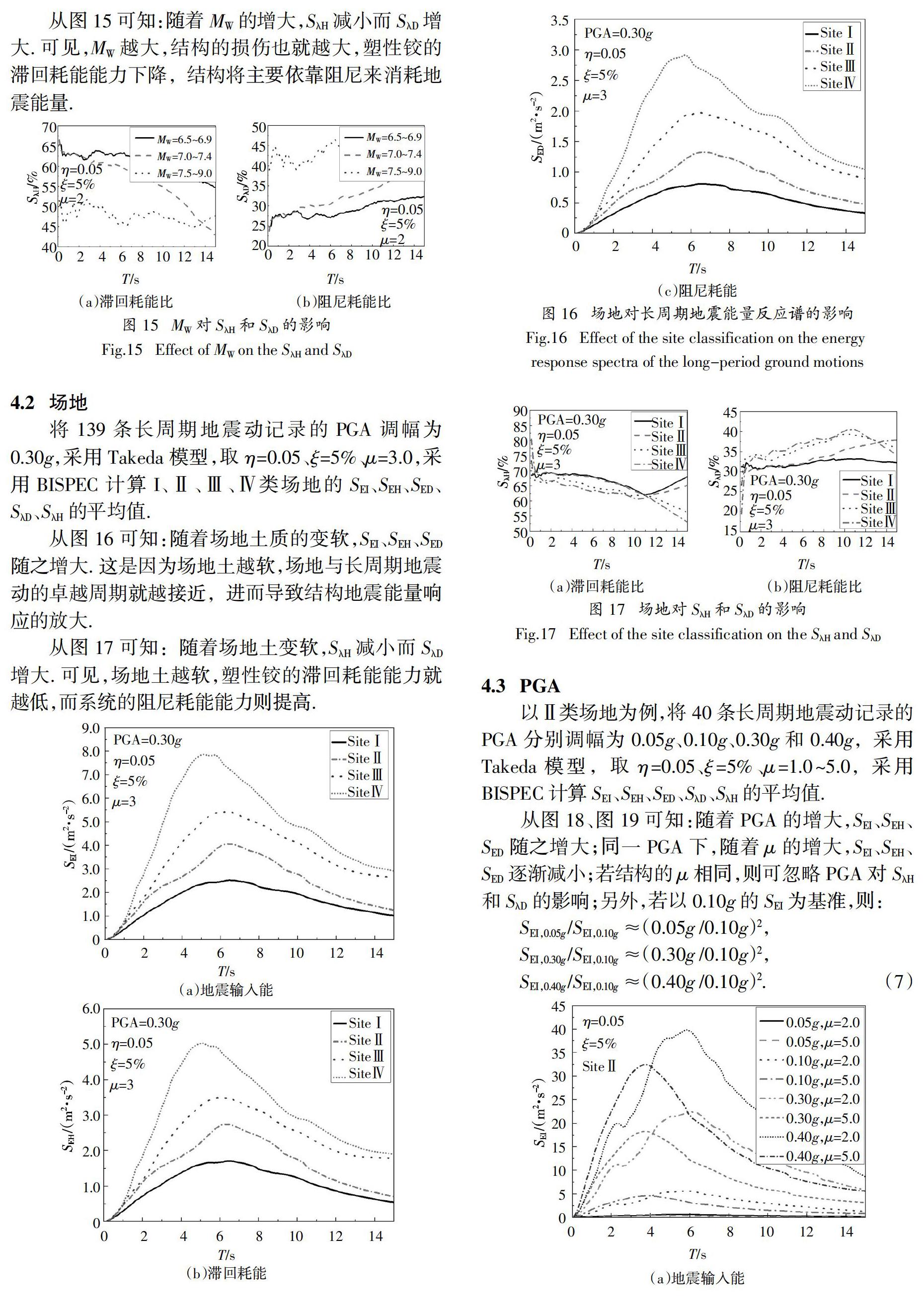
将139条长周期地震动记录的PGA调幅为0.30g，采用Takeda模型，取η=0.05、ξ=5%、μ=3.0，采用BISPEC计算I、Ⅱ、Ⅲ、Ⅳ类场地的SEI、SEH、SED、SλD、SλH的平均值.

从图16可知：随着场地土质的变软，SEI、SEH、SED随之增大. 这是因为场地土越软，场地与长周期地震动的卓越周期就越接近，进而导致结构地震能量响应的放大.

从图17可知：随着场地土变软，SλH减小而SλD增大. 可见，场地土越软，塑性铰的滞回耗能能力就越低，而系统的阻尼耗能能力则提高.

4.3   PGA

以Ⅱ类场地为例，将40条长周期地震动记录的PGA分别调幅为0.05g、0.10g、0.30g和0.40g，采用Takeda模型，取η=0.05、ξ=5%、μ=1.0～5.0，采用BISPEC計算SEI、SEH、SED、SλD、SλH的平均值.

从图18、图19可知：随着PGA的增大，SEI、SEH、SED随之增大;同一PGA下，随着μ的增大，SEI、SEH、SED逐渐减小;若结构的μ相同，则可忽略PGA对SλH和SλD的影响;另外，若以0.10g的SEI为基准，则：

SEI，0.05g /SEI，0.10g ≈（0.05g /0.10g）2，

SEI，0.30g /SEI，0.10g ≈（0.30g /0.10g）2，

SEI，0.40g /SEI，0.10g ≈（0.40g /0.10g）2.      （7）

可見，若已知某基准PGAref下的SEI，ref，则其他PGAoth下的SEI，oth可根据PGAoth与PGAref比值的平方调整得到.

5   长周期地震输入能量设计谱

5.1   长周期地震弹性输入能量设计谱

以139条长周期地震动记录作为输入，采用BISPEC计算四类场地的长周期地震弹性输入能量谱S′ EI的平均值NE1（见图20，PGAref = 0.25g，对于长周期结构取ξ = 2%），再采用三段式拟合函数[18，25]和最小二乘法对NE1进行拟合：

式中：NEI为NEI 的拟合值，即下文的长周期地震弹性输入能量设计谱;NEI max为NEI的平台段峰值;T1为峰值平台起始周期;Tg为峰值平台结束周期;r为衰减指数;Δmin为最小误差.

在此基础上，可得四类场地NEI的拟合参数（见表3），并绘制NEI（见图20），而其他PGA下的NEI可根据4.3节结论，由PGAoth与PGAref比值的平方调整得到.

5.2   长周期地震非弹性输入能量设计谱

5.2.1   μ和ξ对非弹性输入能量谱形状的影响

以Ⅱ类场地为例，将40条长周期地震动记录的PGA调幅为0.25g，采用Takeda模型，并取η = 0.05、ξ = 2%，用BISPEC计算μ = 1.0 ～ 6.0的非弹性输入能量谱（SEI，ξ=2%，μ）和弹性输入能量谱（SEI，ξ=2%，μ=1）的比值R1（见图21），对其拟合后得：

以Ⅱ类场地为例，将40条长周期地震动记录的PGA调幅为0.25g，采用Takeda模型，取η=0.05、μ=4.0，再用BISPEC计算不同ξ的非弹性输入能量谱（SEI，ξ，μ = 4）和ξ = 2%的非弹性输入能量谱（SEI，ξ=2%，μ = 4）的比值R2（图22），对其拟合后得：

同理，其他三类场地的β拟合公式也可用上述方法获得.

5.2.3   建立长周期地震非弹性输入能量设计谱

对5.1节建立的长周期地震弹性输入能量设计谱（图20的NEI）进行调整，以建立长周期地震非弹性输入能量设计谱（PEI）. 步骤如下：

1）将NEImax乘以β，可得PEI的平台峰值PEImax，即PEImax = NEImax × β;

2）将Tg代入式（14）可得K Tg，ξ，μ，再定义谱值调整系数γ（式（16）），将NEI的T > Tg段的谱值乘以γ后，可得到PEI的T > Tg段的谱值.

6   结   论

选取了139条长周期地震动记录作为输入，研究了恢复力模型动力参数和地震动特性对长周期地震能量反应谱的影响，得到以下结论：

1）相比刚度退化模型，无刚度退化模型能量谱的峰值平台、特征周期和中长周期段谱值都要长或大;可以忽略η对长周期地震能量反应谱的影响;ξ对SEI有削峰作用，会增大SEI长周期段谱值，但不改变SEI峰值平台长度和特征周期;μ对SEI和SED有削峰作用，会减小SEI和SEH的特征周期;随着T或μ的增大，各种因素对塑性铰滞回耗能能力和系统阻尼耗能能力的影响减小.

2）与常规地震能量谱的研究结果对比可知： 恢复力模型对常规地震能量谱的影响随着μ的增大而减小，但恢复力模型对长周期地震能量谱的影响则十分显著;无论是何种类型的地震动，η对地震能量谱的影响都可以忽略;ξ对常规地震和长周期地震的SEH和SED影响相同，但是，随着ξ增大，常规地震的SEI的长周期段谱值减小，而长周期地震的SEI的长周期段谱值则增大;μ对常规地震和长周期地震的SEI和SED的影响相同，但是，随着μ增加，常规地震的SEH的峰值平台段后移（往原点方向）、平台段缩短、峰值增大，而长周期地震的SEH的峰值平台段后移、平台段延长、峰值降低.

3）MW越大，结构损伤也越大，使得塑性铰滞回耗能能力下降;场地越软，长周期地震能量谱值越大，塑性铰滞回耗能能力降低，而系统阻尼耗能能力则提高;若已知某基准PGAref下的能量谱，其他PGAoth下的能量谱可根据PGAoth与PGAref比值的平方调整得到.

在此基础上，采用三段式拟合函数，建立了长周期地震弹性输入能量设计谱NEI，并拟合了μ和ξ对长周期地震能量谱的影响公式，进而通过调整NEI谱值，以得到长周期地震非弹性输入能量设计谱PEI，可为长周期结构（如超高层建筑、大跨度桥梁）基于能量的抗震设计提供谱依据.

参考文献

[1]    CHEN Q J，YUAN W Z，LI Y C，et al. Dynamic response characteristics of super high-rise buildings subjected to long-period ground motions[J]. Journal of Central South University，2013，20（5）：1341—1353.

[2]   ASAI T，WATANABE Y. Outrigger tuned inertial mass electromagnetic transducers for high-rise buildings subject to long period earthquakes[J]. Engineering Structures，2017，153：404—410.

[3]    HU R P，XU Y L，ZHAO X. Long-period ground motion simulation and its impact on seismic response of high-rise buildings[J]. Journal of Earthquake Engineering，2018，22（7）：1285—1315.

[4]    ZHOU Y，PING T Y，GONG S M，et al. An improved defining parameter for long-period ground motions with application of a super-tall building[J]. Soil Dynamics and Earthquake Engineering，2018，113：462—472.

[5]    姬淑艳，刘烁宇，李英民. 远场长周期地震动作用下超高层建筑响应特性[J]. 建筑结构学报，2018，39（11）：1—10.

JI S Y，LIU S Y，LI Y M. Response characteristics of super high-rise  building subjected to far-field long-period ground motion[J]. Journal of Building Structures，2018，39（11）：1—10. （In Chinese）

[6]    SHEKARI M R. A coupled BE-FE-BE study for investigating the effect of earthquake frequency content and predominant period on seismic behavior of base-isolated concrete rectangular liquid tanks[J]. Journal of Fluids and Structures，2018，77：19—35.

[7]    MAZZA F. Seismic demand of base-isolated irregular structures subjected to pulse-type earthquakes[J]. Soil Dynamics and Earthquake Engineering，2018，108：111—129.

[8]    ISMAIL M，RODELLAR J，CASAS J R. Seismic behavior of RNC-isolated bridges：a comparative study under near-fault，long-period，and pulse-like ground motions[J]. Advances in Materials Science and Engineering，2016，2016：1—18.

[9]   MAZZA F. Nonlinear modeling and analysis of R. C. framed buildings located in a near-fault area[J]. The Open Construction and Building Technology Journal，2012，6（1）：346—354.

[10]  BAI Y T，GUAN S Y，LIN X C，et al. Seismic collapse analysis of high-rise reinforced concrete frames under long-period ground motions[J]. Structural Design of Tall Buildings，2019，28（1）：e1566.

[11]  HUO T，TONG L W，ZHANG Y F. Dynamic response analysis of wind turbine tubular towers under long-period ground motions with the consideration of soil-structure interaction[J]. Advanced Steel Construction，2018，14（2）：227—250.

[12]  建筑抗震設计规范：GB50011—2010 [S]. 北京：中国建筑工业出版社，2016：18—20.

Code for seismic design of buildings：GB 50011—2010[S]. Beijing：China Architecture & Building Press，2016：18—20. （In Chinese）

[13]  铁路工程抗震设计规范：GB50111—2006[S]. 北京：中国计划出版社，2009：9—10.

Code for seismic design of railway engineering：GB50111—2006[S]. Beijing：China Planning Press，2009：9—10. （In Chinese）

[14]  公路桥梁抗震设计规范：JTGT 2231-01—2020[S]. 北京：人民交通出版社，2020：23—24.

Specifications for seismic design of highway bridges：JTGT 2231-01—2020 [S]. Beijing：China Communications Press，2020：23—24. （In Chinese）

[15]  张亮泉，于建杰. 基于遗传算法的长周期地震动加速度反应谱的拟合[J]. 自然灾害学报，2019，28（6）：17—27.

ZHANG L Q，YU J J. Study on the fitting of the long-period ground motion acceleration response spectrum based on genetic algorithm[J]. Journal of Natural Disasters，2019，28（6）：17—27. （In Chinese）

[16]  李宇，吴桂楠，李琛，等. 长周期地震动弹塑性反应谱的参数影响[J]. 兰州大学学报（自然科学版），2018，54（1）：90—97.

LI Y，WU G N，LI C，et al. Parametric impact on elasto-plastic response spectra of long-period ground motion[J]. Journal of Lanzhou University （Natural Sciences），2018，54（1）：90—97. （In Chinese）

[17]  ZHOU J，JIANG Y，WANG L X，et al. A long-period elastic response spectrum based on the site-classification of Chinese seismic code[J]. Soil Dynamics and Earthquake Engineering，2018，115：622—633.

[18]  陈清军，袁伟泽. 基于长周期地震动记录的SDOF体系能量谱探讨[J]. 振动与冲击，2013，32（10）：36—42.

CHEN Q J，YUAN W Z. Energy spectrum of SDOF system based on long-period ground motion records[J]. Journal of Vibration and Shock，2013，32（10）：36—42. （In Chinese）

[19]  刘烁宇，李英民. 盆地型长周期地震动的判别准则[J]. 湖南大学学报（自然科学版），2018，45（5）：85—93.

LIU S Y，LI Y M. Discriminant criterion of long-period ground motion in basin[J]. Journal of Hunan University （Natural Sciences），2018，45（5）：85—93. （In Chinese）

[20]  刘培玄，刘红帅，赵纪生，等. 基于KiK-net台站的中美场地类别对比分析[J]. 地震工程与工程振动，2015，35（6）：42—46.

LIU P X，LIU H S，ZHAO J S，et al. Comparison of site classification between Chinese and American seismic codes based on data of Japanese Ki K-net station[J]. Earthquake Engineering and Engineering Dynamics，2015，35（6）：42—46. （In Chinese）

[21]  HOUSNER G W. Behavior of structures during earthquakes[J]. Journal of the Engineering Mechanics Division，1959，85（4）：109—129.

[22]  CHOU C C，UANG C M. Establishing absorbed energy spectra—an attenuation approach[J]. Earthquake Engineering & Structural Dynamics，2000，29（10）：1441—1455.

[23]  李宇. 考虑残余位移和土-结构相互作用的桥梁结构基于性能的抗震设计及评估[D]. 北京：北京交通大学，2010：31—33.

LI Y. Research on performance-based seismic design and evaluation for bridge structures considering residual displacement and soil-structure interaction effects[D]. Beijing：Beijing Jiaotong University，2010：31—33. （In Chinese）

[24]  李宇，车艳阳，王森. 梁式桥抗震设计的地震能量反应谱分析[J]. 土木工程学报，2015，48（1）：82—89.

LI Y，CHE Y Y，WANG S. Study on seismic energy response spectra for beam-bridge seismic design[J]. China Civil Engineering Journal，2015，48（1）：82—89. （In Chinese）

[25]  程光煜，葉列平. 弹塑性SDOF系统累积滞回耗能谱[J]. 工程抗震与加固改造，2007，29（2）：1—7.

CHENG G Y，YE L P. Cumulative hysteretic energy spectra of SDOF systems[J]. Earthquake Resistant Engineering and Retrofitting，2007，29（2）：1—7. （In Chinese）