考虑寄生振荡的IGBT分段暂态模型对电磁干扰预测的影响分析
黄华震 仝 涵 王宁燕 卢铁兵
考虑寄生振荡的IGBT分段暂态模型对电磁干扰预测的影响分析
黄华震1仝 涵1王宁燕2卢铁兵1
(1. 新能源电力系统国家重点实验室(华北电力大学)北京 102206 2. 国网福建电科院 福州 350003)
绝缘栅双极型晶体管(IGBT)开关过程的d/d和d/d是影响换流器电磁干扰(EMI)水平的主要因素。IGBT的寄生振荡是高频EMI的重要组成部分,振荡频点处会出现EMI峰值。该文提出一种考虑寄生振荡的IGBT分段暂态模型,分析回路寄生参数和器件非线性电容对开关特性的影响,分别计算不同阶段的电流和电压变化率。搭建二极管钳位感性负载测试平台,获取IGBT的电流和电压波形,分析对比分段模型和实际波形的频谱特性。最后,通过实验验证了模型中的振荡过程是影响电流频谱特性的关键,且采用器件电容gc的三段等效模型可以显著提高电压频谱预测的准确度。该文提出的模型提高了IGBT干扰源频谱的预测准确度,可用于评估实际换流器发射的EMI水平。
绝缘栅双极型晶体管 分段暂态模型 寄生振荡 频谱
0 引言
绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT)自1985年得到实际应用后,逐渐成为电力电子的主流器件[1]。经过三十多年的研究与发展,IGBT技术已经较为成熟,在直流输电工程、铁路、变速驱动器等领域得到了广泛应用。近年来,以IGBT作为核心器件的模块化多电平换流器(Module Multilevel Converter, MMC)柔性直流输电技术发展迅速,在分布式能源并网、孤岛供电、城市电网供电和多端直流电网等多种应用场合都具有重要意义[2-6]。然而,IGBT器件开关过程会产生快速变化的电压和电流,其上升沿和下降沿包含很多高频成分,通过传导和辐射的耦合方式产生了不可忽略的电磁干扰(Electromagnetic Interference, EMI)问题[7-9]。随着柔性直流输电技术和电网建设的快速发展[10],更高电压、更大容量的IGBT将会成为直流电网建设的主流需求,同时会带来更为复杂化的EMI问题。
对于电力电子换流器的EMI问题,通常会在换流器的输入端插入EMI滤波器来抑制传导干扰,以及通过屏蔽来减少辐射干扰水平[11-14]。在换流器开发结束后,加入滤波器或屏蔽等电磁干扰抑制装置,通过电磁兼容测试,判断该换流器是否满足电磁兼容标准[15]。如果测试结果不满足要求,需要对换流器的电磁干扰抑制措施做进一步的改善并重新测试,导致换流器开发周期的延长。因此,在电力电子换流器的设计开发阶段,建立有效的电磁干扰模型来预测换流器系统的电磁干扰水平是很有必要的[16-17]。
IGBT的快速开关动作是功率换流器电磁干扰的主要来源,而开关过程的d/d和d/d是决定电磁干扰发射水平的关键参数[18]。对IGBT开关瞬态波形的调制也是抑制EMI的有效措施[19-20]。建立有效的干扰源模型是换流器EMI预测的关键。目前,针对结温分析、损耗预测等需求的IGBT模型比较丰富,但针对EMI预测的IGBT模型并不完善。电压和电流的变化速率是IGBT电磁干扰模型的主要关注对象。现有文献通常采用较为简化的阶梯波形来模拟IGBT的开关过程,该建模方法包含的有效频率成分很少,导致模型的EMI预测准确度较低,适用频率范围较窄。文献[21]采用改进的S阶梯波代替IGBT的电压变化过程,可以有效抑制EMI的高频分量,但是与实际开关波形差异较大,模型的EMI预测效果未得到实验的验证。IGBT的开关特性受到自身的器件参数以及外部电路参数的影响,暂态过程非常复杂,不能将其开关过程用单一斜率的d/d和d/d来表示[22]。采用曲线拟合的方式对IGBT进行建模能够得到较好的模型准确度,但该建模方法在不同工况条件下的适用性较差[23-25]。此外,回路中寄生电感与电容的相互作用会在IGBT开关过程中引入高频振荡,使得EMI问题更为严重。
本文首先按照不同的时间阶段对IGBT的开关暂态波形进行建模分析,考虑了寄生参数和器件电容变化对开关特性的影响,并分别计算了不同阶段的d/d和d/d。为了有效地反映寄生振荡现象对EMI特性的影响,模型中合理地考虑了IGBT的开通振荡过程。最后搭建了二极管钳位感性负载测试平台,通过实验验证了电压电流分段模型可有效用于IGBT开关过程的电磁干扰特性预测,并分析了寄生振荡和gc对频谱特性的影响。
1 IGBT开关等效电路
为了详细分析IGBT的开关暂态过程及影响参数,采用如图1所示的二极管钳位感性负载电路,该电路考虑了所有影响IGBT开关特性的器件自身参数与外部电路参数。图中,g为栅极电压,g为栅极驱动电阻,g和e分别为栅极电感和发射极电感,包括外部电路和器件自身封装引入的电感;e对栅极-发射极电压ge有反馈作用,因此对IGBT的开关特性影响较大;c1为器件内部和电路板布线引入的集电极电感,c2为母排路径引入的电感,总集电极电感c=c1+c2;loop为开关回路的总寄生电阻;为了分析开关过程引入的寄生振荡问题,二极管自身的结电容D与负载电感引入的寄生电容L是不可忽视的,电流过冲阶段电容F=D+L;dc为母线电压,bus为母线电容。
IGBT的开关特性主要取决于栅极-发射极电容ge、栅极-集电极电容gc和集电极-发射极电容ce的充放电过程。因此,器件电容的等效模型会很大程度地影响IGBT的建模精度。其中,ge主要由栅极-发射极金属电容和氧化层电容组成,其电容值可认为是一个固定值,不随器件电压的变化而变化。然而,gc和ce的电容值会随着器件集电极电压的变化而变化,尤其是栅极-集电极电容gc,对IGBT的栅极电压具有反馈调节作用,是IGBT动态建模的关键[26]。gc和ce随电压的变化过程可以表示为()=0/(1+/),参数和从电容-电压的关系曲线获取,0为电压为0时的电容值。由于电容的变化主要集中在几十伏的电压范围内,本着简化模型的目标,通常将gc和ce等效为两个离散值,器件电容的等效模型如图2所示。具体的电容值及约束条件见表1。其中,gc2gc1,ce2ce1。上述电容的等效模型简单描述了IGBT的非线性开关过程,但模型的误差还需要进一步分析。
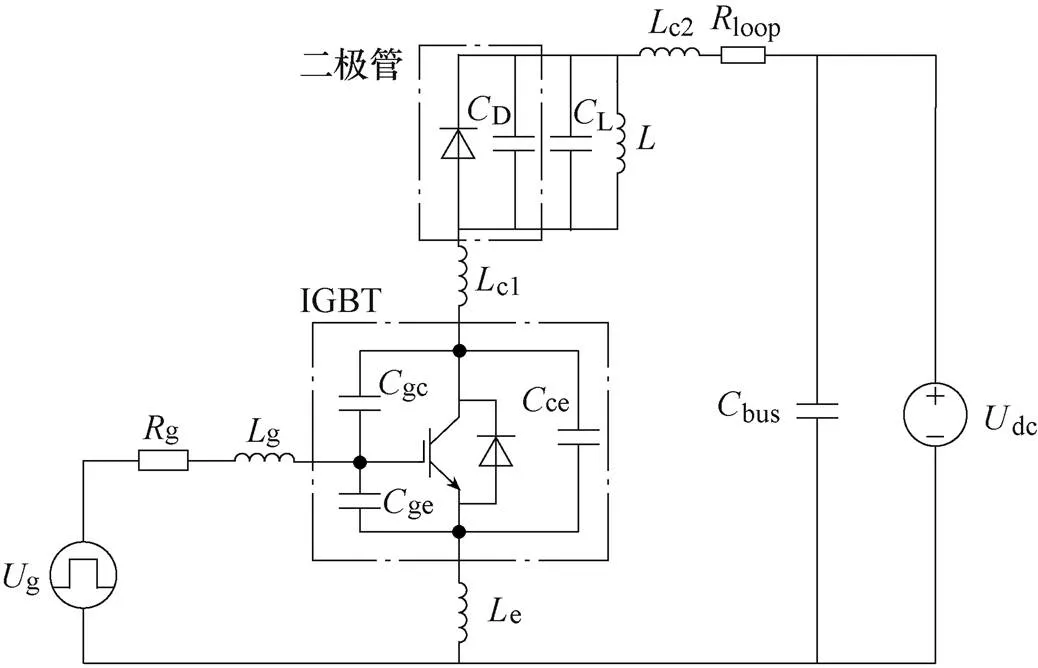
图1 IGBT开关等效电路
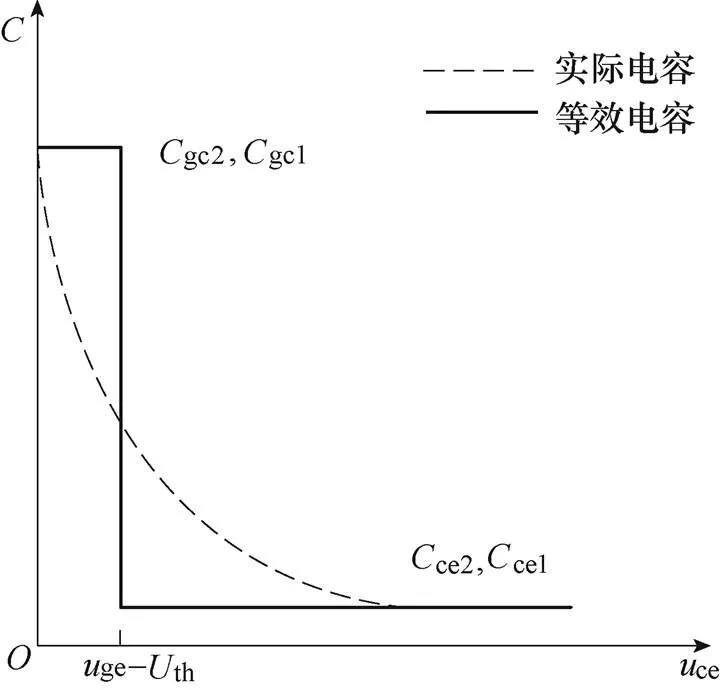
图2 器件电容的等效模型
表1 器件电容的等效值
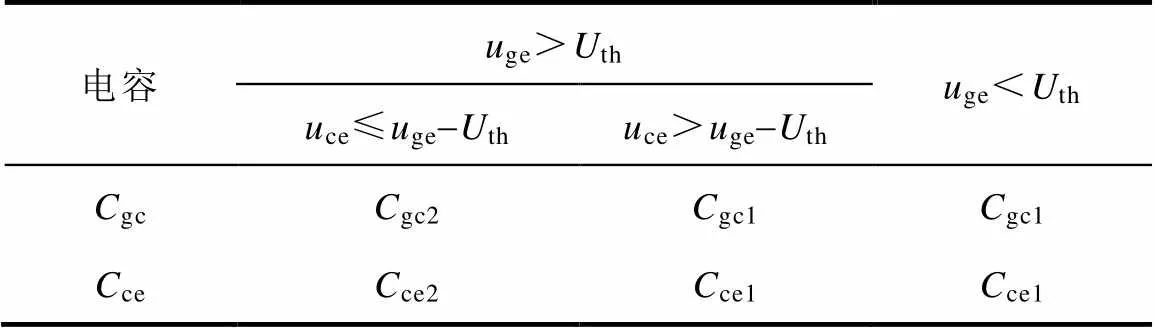
Tab.1 The equivalent value of device capacitances
2 IGBT分段暂态模型
基于图1所示的IGBT开关等效电路,对IGBT的开关暂态过程进行详细建模,建模过程考虑了所有寄生参数以及器件非线性电容的影响。d/d和d/d是影响换流器EMI水平的关键因素,开关过程在不同阶段的d/d和d/d会对EMI水平有不同程度的影响。同时,IGBT开关速度较快时,回路中寄生电容和电感的相互作用使得开关过程结束后出现寄生振荡现象,在振荡频点附近造成较大的EMI峰值,需要重点考虑。因此,本文分阶段分析IGBT的电压和电流变化速率,每个阶段采用单一的d/d和d/d来表示,考虑IGBT的开通电流振荡过程,建立了考虑寄生振荡的IGBT分段暂态模型。图3所示为IGBT分段开关波形。
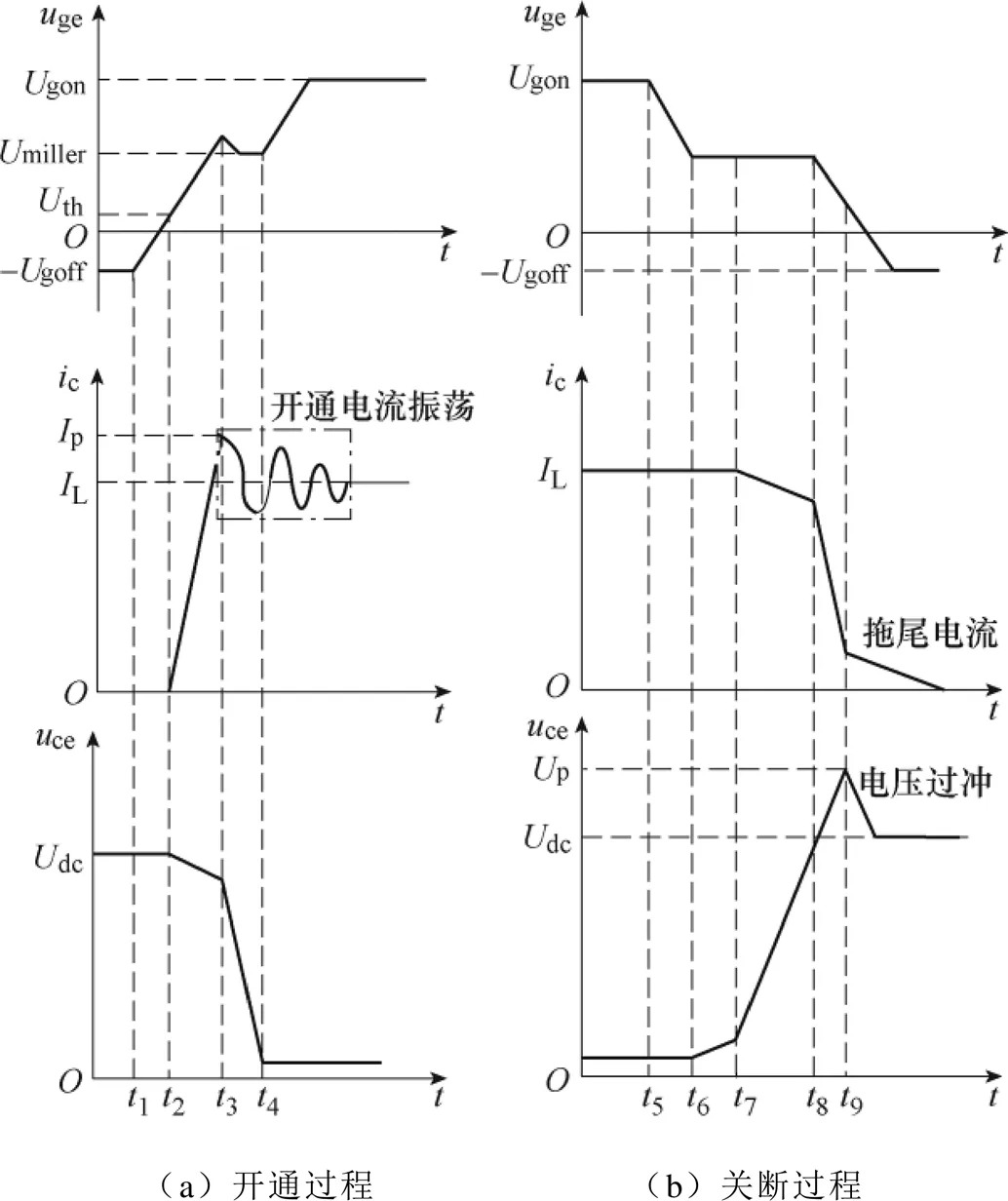
图3 IGBT分段开关波形
2.1 开通暂态模型
2.1.1 开通延时
图3a为IGBT的开通波形分段示意图。1时刻,门极驱动电压从负压-goff跳变为正压gon时,gon开始给输入电容iss(iss=ge+gc)充电直至IGBT的栅极-发射极电压ge达到阈值电压th。ge的充电方程为
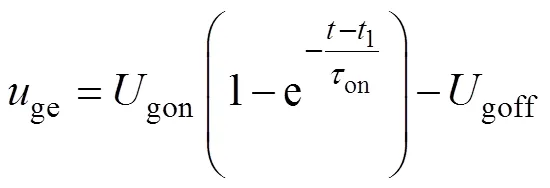
式中,on为开通延时,on=g(ge+gc1)。
2.1.2 电流上升
ge在2时刻达到阈值电压th,IGBT开始导通,集电极电流开始快速上升。该阶段IGBT的集电极电流c可表示为
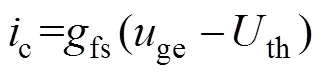
式中,fs为IGBT的跨导。
为了进一步求解2~3阶段的电流上升率,列写栅极电流g和驱动回路的电压方程(忽略栅极电感的影响)为
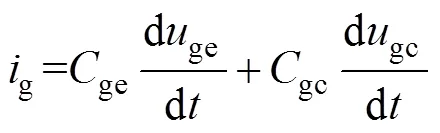
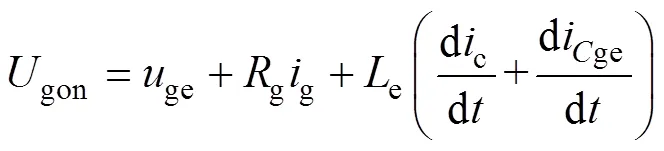
式中,gc为栅极-集电极电压;ige为流过ge的电流。
由于回路中寄生电感的存在,快速变化的电流在寄生电感上产生压降,导致器件电压也会有部分下跌。
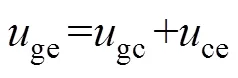
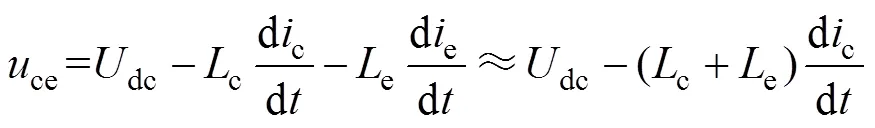
式中,ce为集电极-发射极电压;e为发射极电流。
联立式(2)~式(6),可得关于ge的二阶常系数齐次线性微分方程为
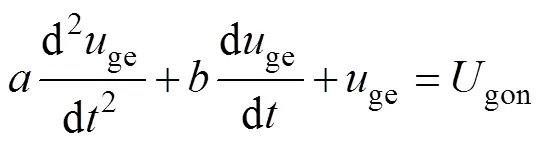
式中,=fsggc(c+e)+ege;=fse+g(ge+gc),gc=gc1。
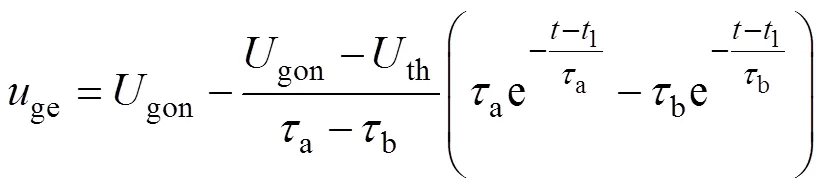
其中
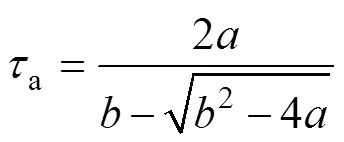
结合式(2)和式(8),可知2~3阶段的集电极电流上升斜率[27]为
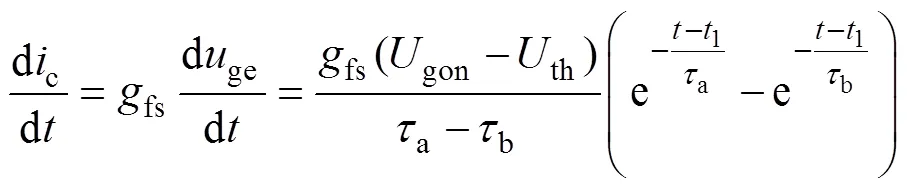
对式(9)进行泰勒级数展开,求得达到稳态电流时的电流斜率如式(10)所示,并用该电流斜率作为2~3阶段IGBT的电流上升速率。
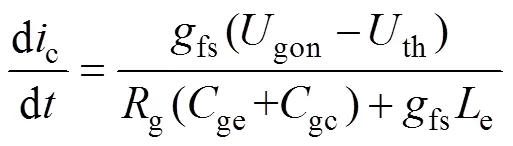
式中,gc=gc1。
当集电极电流达到稳态电流L后,会出现电流过冲现象。为了避免二极管反向恢复过程给IGBT带来的电流过冲损坏,本文采用碳化硅肖特基二极管,但二极管的结电容和负载电感的寄生电容也会造成IGBT开通过程的电流过冲现象。如图1所示,二极管和负载电感引入的总电容为F=D+L,电流过冲阶段电容F的电压F和电流F分别为
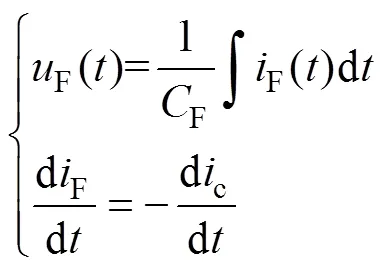
因此,电流c从L上升至峰值电流p所需的时间为
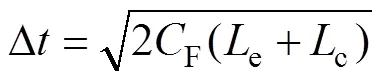
结合式(10)和式(12),IGBT开通过程中的电流过冲值为
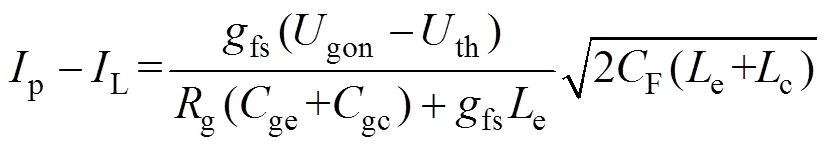
根据p和电流上升斜率,可以求得电流上升时间2~3。因此,该阶段电压的下降斜率为

2.1.3 电压下降
1.晚餐为人体提供能量。晚餐和早餐、午餐一样,都可以为人体提供能量。不吃晚餐,胃酸也会照常分泌,但因为没有食物提供分解,长此以往,胃酸会伤害胃黏膜,久而久之,很容易导致胃黏膜糜烂、溃疡,抵抗力减弱。所以,胃不好的人,三餐要按时吃。
3时刻IGBT的电流达到最大值p,然后二极管反向偏置,集电极电压开始快速下降。3~4阶段为米勒平台阶段,器件的栅极-发射极电压变化很小,栅极电流全部流过gc。该阶段电压的下降斜率[18]可以表示为
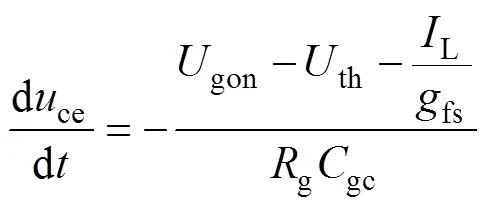
式中,gc=gc1。
2.1.4 开通电流振荡
3时刻后,开关回路中寄生电感和寄生电容互相作用,导致IGBT的电流过冲会有一段振荡衰减的过程。器件在开通状态时可等效为短路,因此开通振荡等效电路如图4所示,令loop=e+c1+c2。电流过冲会在RLC电路中呈指数规律衰减,开通振荡阶段的器件电流为
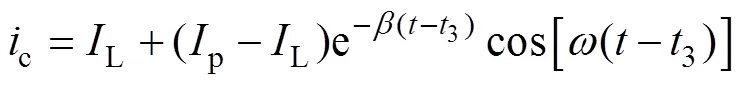
式中,b =Rloop/(2Lloop);w =[1/(LloopCF)-b2]1/2。因此,开通振荡频率f=w/(2p),振荡频率主要受回路寄生电感Lloop和寄生电容CF的影响。电流过冲的衰减速度由回路电阻Rloop和Lloop共同决定。
2.2 关断暂态模型
2.2.1 关断延时
对IGBT的关断暂态过程进行分段建模。图3b为IGBT的关断波形分段示意图。5时刻,驱动电压从正压gon跳变为负压-goff,并通过栅极电阻和输入电容给IGBT的栅极-发射极电压ge放电,直到ge下降至米勒平台电压。ge的放电方程为
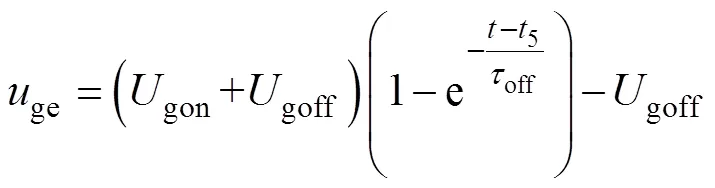
式中,on为关断延时,on=g(ge+gc2)。
6~9阶段为电压的上升阶段。该阶段ge保持平台电压不变,栅极电流主要给gc充电。基于图2所示的离散电容模型,将该阶段IGBT电压上升过程分为6~7和7~9两个阶段:6~7阶段,gc=gc2;7~9阶段,gc=gc1。两个阶段的电压上升速率为
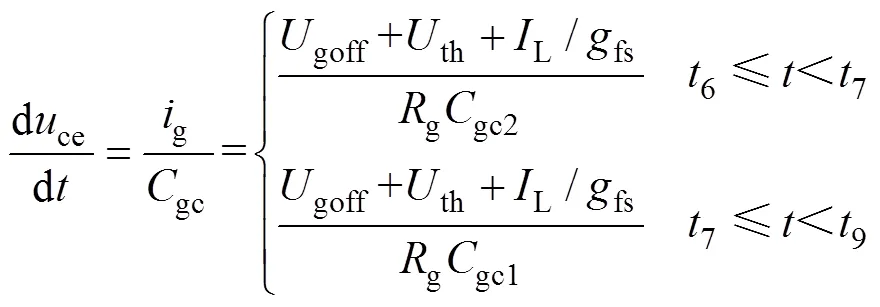
因此,电压上升阶段的前半段电压上升速率较小,后半段随着电压的增大其上升速率也增大。7时刻后,由于电压的快速上升,使二极管和负载电感的寄生电容上开始流过电流,IGBT集电极电流会有部分下跌。7~8阶段的电流下降斜率可以表示为
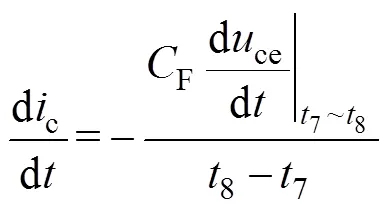
2.2.3 电流下降
8时刻,ce上升到母线电压,续流二极管正向偏置,开始为电感电流提供续流通路,因此器件电流c开始快速下降。该阶段ge从米勒平台电压开始下降,驱动回路方程为
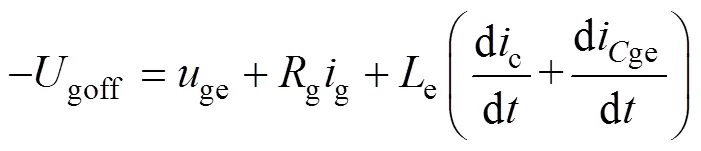
对于IGBT关断过程电流快速下降阶段的分析方法与2~3阶段相同。联立式(2)、式(3)、式(5)、式(6)和式(20),可得
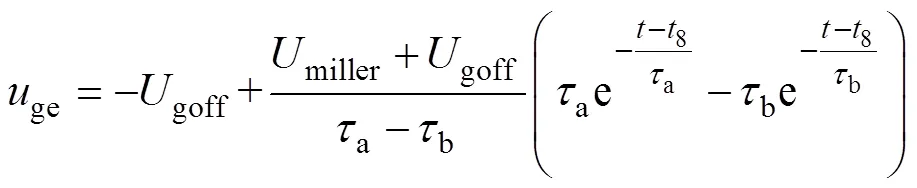
式中,miller为米勒平台电压,miller=th+L/fs。
因此,该阶段的电流下降斜率[27]为
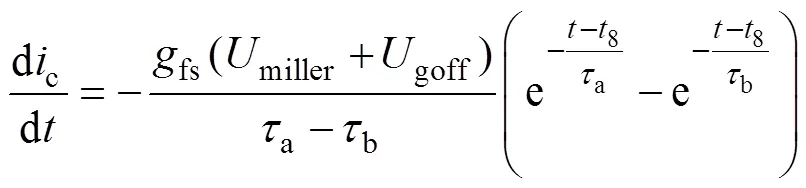
对式(22)做泰勒级数展开,可得8~9阶段的电流下降斜率为
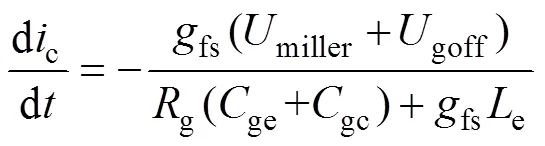
寄生电感与快速变化的电流会导致关断过程的电压过冲,电压峰值为
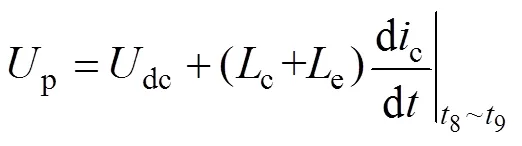
2.2.4 拖尾电流
9时刻后,集电极电流c不会立刻降为0,而是进入缓慢减小的拖尾电流阶段。随着拖尾电流缓慢下降,ge也继续下降,直到IGBT完全关断。通常采用指数函数[24]来模拟拖尾电流的下降过程为
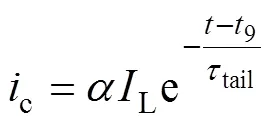
式中,为初始拖尾电流与稳态电流的比值;tail为拖尾时间常数。
拖尾现象与IGBT的制造技术、电荷载流子寿命、结温等条件有关,因此式(25)的相关参数取决于IGBT芯片的内部结构,无法基于外部电路模型分析拖尾电流特性。通常需要借助实验波形对拖尾电流过程进行建模。根据关断电流特性,拖尾时间常数tail近似取为电流拖尾总时间tail的1/4[24]。本文中拖尾电流阶段采用单一斜率进行建模,拖尾总时间从实验波形中获取。拖尾电流可表示为
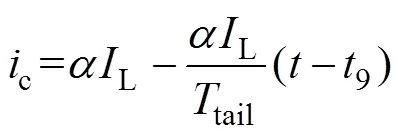
需要注意的是,借助关断电流波形对IGBT拖尾电流进行建模会降低电流模型的适用性。如图3所示,2~3为电流快速上升阶段,8~9为电流快速下降阶段,这两个阶段的电流变化速率很快,是造成大量电磁干扰的主要原因。而拖尾阶段电流呈现缓慢下降趋势,该阶段包含的高频成分很少,对于电流模型的EMI预测准确度影响较小。在缺少实验条件下,建议电流模型中可以忽略电流拖尾过程,电流从8时刻快速下降至0。
3 实验平台及参数提取
3.1 实验平台
为了验证上述模型对IGBT产生EMI的预测分析,搭建了如图5所示的二极管钳位感性负载测试平台,用于获取IGBT的开关暂态波形。测试平台采用光纤传输双脉冲信号至驱动电路板,驱动芯片采用IXDI609SI,驱动电压为+15V/-4V,确保IGBT能够稳定地开通和关断。母排电容由四个900V/ 50mF的薄膜电容并联组成,由直流电源对母排电容充电提供测试平台所需的电压要求。IGBT采用Infineon公司1 200V/40A的单器件,同时采用碳化硅肖特基二极管以避免反向恢复过程。负载电感为0.48mH的空心电感,电感值的选取与稳态电流的上升斜率有关。
IGBT电压和电流的快速变化过程是影响EMI水平的关键因素,因此开关电压和电流的准确测量至关重要。本文采用无源高压探头和电流线圈测量IGBT的暂态电压和电流,其主要参数见表2。测量设备的带宽可以满足开关波形的测量要求。同时,采用Tektronix MD03034示波器来记录获取的电压和电流波形,其带宽为350MHz,最大采样率可达2.5GS/s。

图5 实验测试平台
表2 测量设备的主要参数

Tab.2 Main parameters of measured equipment
3.2 参数提取
器件参数和电路参数的准确提取有助于提高模型的精度。首先,采用功率分析仪测量IGBT器件的阈值电压、跨导系数和不同极之间的电容值。其中,th=5.78V,fs=8.76S。栅极-发射极电容ge= 2 143pF。栅极-集电极电容gc与集电极-发射极电容ce与器件电压有关,实测电容的等效模型如图6所示。由图可知,gc和ce在几十伏的电压范围内,电容值随着电压升高迅速下降,然后缓慢减小至稳定值。根据测量结果,建立gc和ce的等效模型,将其分别等效为图6所示的两个离散电容:gc1= 35.5pF,gc2=1 220pF;ce1=30pF,ce2=642pF。
开关回路中的寄生电感对IGBT的开关特性有较大的影响。由式(24)可知,通过关断过程的电压过冲值和电流变化率可以大致计算回路中的总寄生电感。表3给出了不同电流等级下的寄生电感计算结果,取均值loop=179nH。回路寄生电阻与电流振荡的衰减特性相关,对于电流振荡过程引起的EMI水平有较大的影响。采用阻抗分析仪测量了整个测试平台的寄生电阻。目前针对回路寄生电感有较多的优化提取方法[28],但很少对寄生电阻的测量方法展开讨论。寄生电阻的准确提取可以更精确地描述电流模型的振荡衰减过程。此外,发射极电感e对器件的ge有反馈作用,直接影响IGBT电流的变化率。e主要由PCB的发射极路径和IGBT封装寄生电感构成。采用电磁场仿真软件计算PCB路径引入的发射极电感为32.5nH,而IGBT的封装管脚引入的发射极电感约为13nH[29]。因此,总发射极电感e=45.5nH。
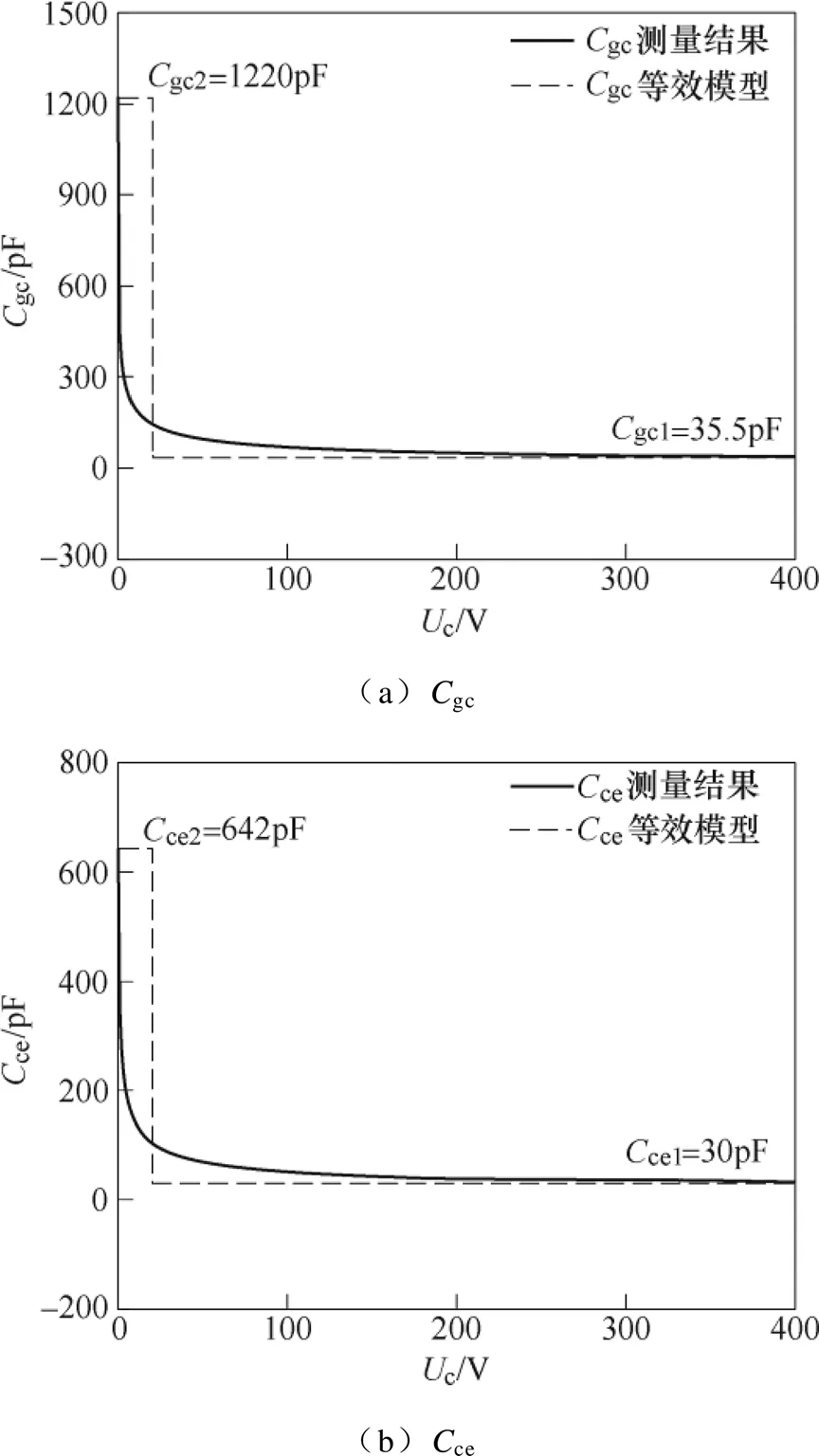
图6 实测电容的等效模型
表3 回路寄生电感的计算结果

Tab.3 Calculation results of loop parasitic inductance
二极管和负载电感引入的总寄生电容F与IGBT开通过程的振荡频率有关。二极管自身的结电容可从数据手册获取,D=45pF。采用阻抗分析仪Agilent4294A测量了负载电感的阻抗特性,其曲线如图7所示。负载电感阻抗曲线的谐振频率为766kHz,由式(27)可以计算出其寄生电容为L=90pF。因此,F=D+L=135pF。
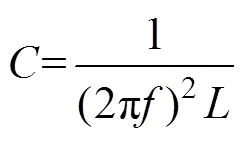
4 EMI预测分析及讨论
IGBT换流器的传导和辐射干扰特性不仅取决于IGBT的开关动作,还取决于换流器内部的传导耦合路径和周围的空间电磁环境。对实际换流器发射的EMI水平进行评估预测是非常困难的,也很难得出普遍适用的结论。IGBT的开关过程是产生EMI高频能量的干扰源。通常,对换流器的传导干扰路径或者实际结构进行建模,采用IGBT开关波形的频谱分量作为干扰源,由此可以计算得到换流器在不同应用条件下的传导或辐射干扰水平,并进一步分析换流器的EMI特性。在换流器结构相似的情况下,干扰源的差异决定了换流器EMI水平的不同。因此,采用开关波形的频域分析代替直接的传导或辐射干扰测试,使得测量结果可以独立于特定的换流器来进行比较。本文建立了IGBT开关暂态模型,用于预测IGBT开关波形的频谱分量,基于图5所示的测试平台与测量设备获取了IGBT的开关电流和电压,对模型的EMI预测准确度进行验证。
4.1 电流频谱预测
结合2.1节、2.2节的电流暂态过程分析,以及3.2节提取的实验参数,建立IGBT开关暂态电流分段模型。对IGBT电流的测量波形和分段模型做傅里叶变换,验证上述电流模型对实测电流波形频谱的预测准确度。实验和分段模型的电流频谱对比如图8所示。
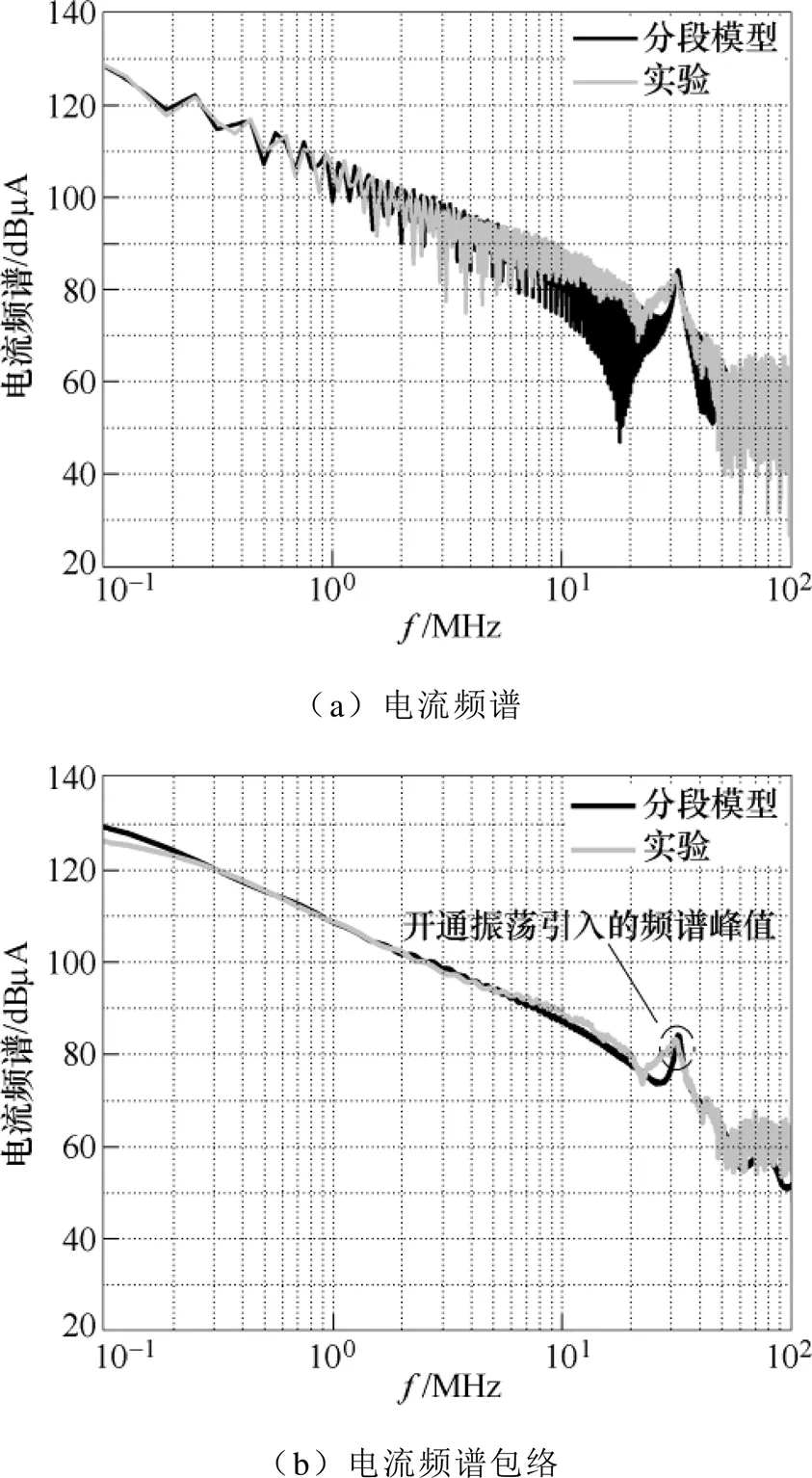
图8 实验和分段模型的电流频谱对比
图8a为分段电流模型与电流实验波形的频谱对比。在实际应用中频谱峰值是人们更关注的,图8b对比了实验和模型的电流频谱包络。由图8可知,考虑振荡的IGBT分段电流模型可以较好地预测实际电流波形的频谱分量,并追踪到开通寄生振荡引入的电流频谱峰值。在实际应用中,IGBT的寄生振荡现象会造成振荡频点处出现EMI峰值,需要对此加以关注,必要时进行抑制。在50MHz以上的高频段,电流模型频谱与实际电流波形频谱存在10dB内的误差,这主要是由电流模型的快速上升阶段引起的。电流在2~3快速上升阶段包含大量高频成分,采用式(10)的单一斜率来近似描述该过程必然造成模型中的部分高频成分缺失,这也是线性模型的局限性。因此,可以继续完善2~3阶段的IGBT电流模型,进一步提高模型在高频段EMI预测的适用性。
很多电磁干扰预测模型详细考虑了IGBT快速开关过程中的d/d和d/d,通过精确描述电压电流的变化速率来提高EMI预测的准确性,却忽略了寄生振荡的影响。开关速度较快时,IGBT的电流过冲伴随着明显的振荡衰减过程,而寄生振荡会对电流波形频谱的高频分量造成较大的影响。本文对比了考虑振荡的分段电流模型与不考虑振荡的模型对EMI预测的结果,振荡模型与无振荡模型的电流频谱对比如图9所示。不考虑振荡的电流模型频谱在振荡频点附近与实验结果差异明显,丢失了电流频谱在振荡频点出现峰值这一关键信息。因此,当IGBT开关速度较快并引入较为剧烈的开通振荡现象时,需要对振荡频率进行预判,重点考虑振荡频点处的EMI水平。
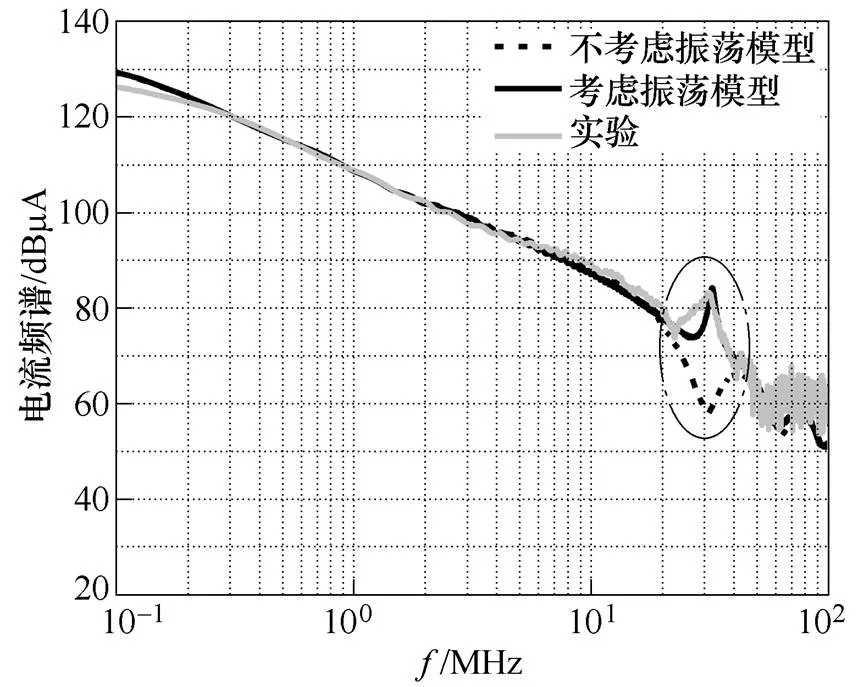
图9 振荡模型与无振荡模型的电流频谱对比
IGBT拖尾电流需要借助开关电流波形进行建模,通过实验进一步验证拖尾电流过程与EMI的关系。图10所示为考虑拖尾电流模型与不考虑拖尾电流模型的对比。由于电流快速下降阶段的延长,不考虑拖尾电流的模型在1~6MHz范围内的频谱幅值略高于考虑拖尾电流的模型,与实验电流波形频谱的差异为几dB。在缺少实验条件下,可以忽略拖尾电流过程,但电流模型在低频段的EMI预测准确度会有所下降。值得注意的是,若不考虑拖尾电流过程,本文的建模方法也适用于MOSFET器件的EMI分析,但其预测效果需要进一步的实验验证。
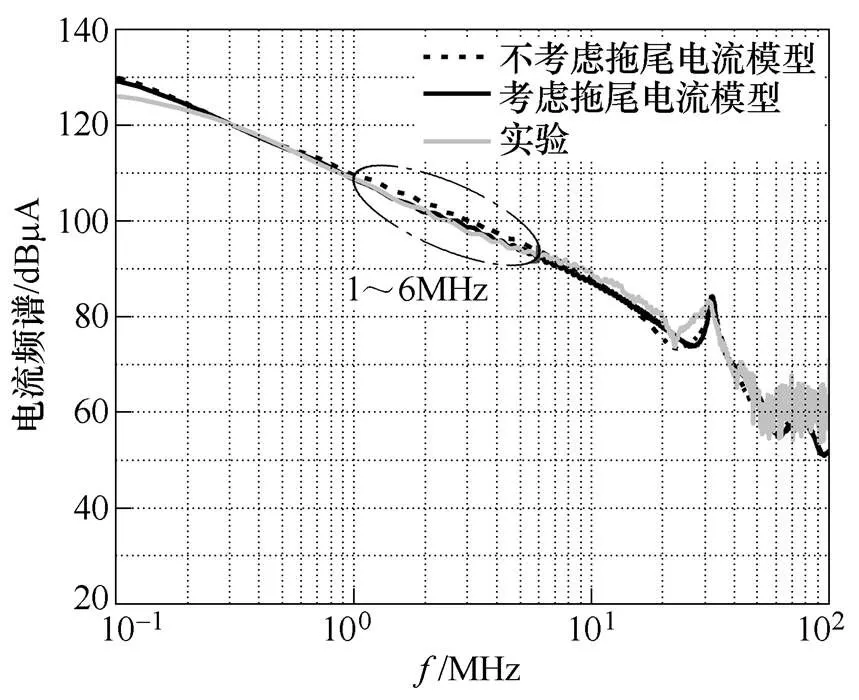
图10 考虑拖尾电流模型与不考虑拖尾电流模型的对比
4.2 电压频谱预测
实验测量与分段电压模型的电压波形频谱对比如图11所示。从图中可以明显看出,分段电压模型在低频段和40MHz以上的高频段对实际电压波形频谱能起到较好的预测效果。然而,在4~40MHz频率范围内,电压模型的频谱比实际波形要高出几dB到10dB左右,这主要是由gc模型的误差造成的。
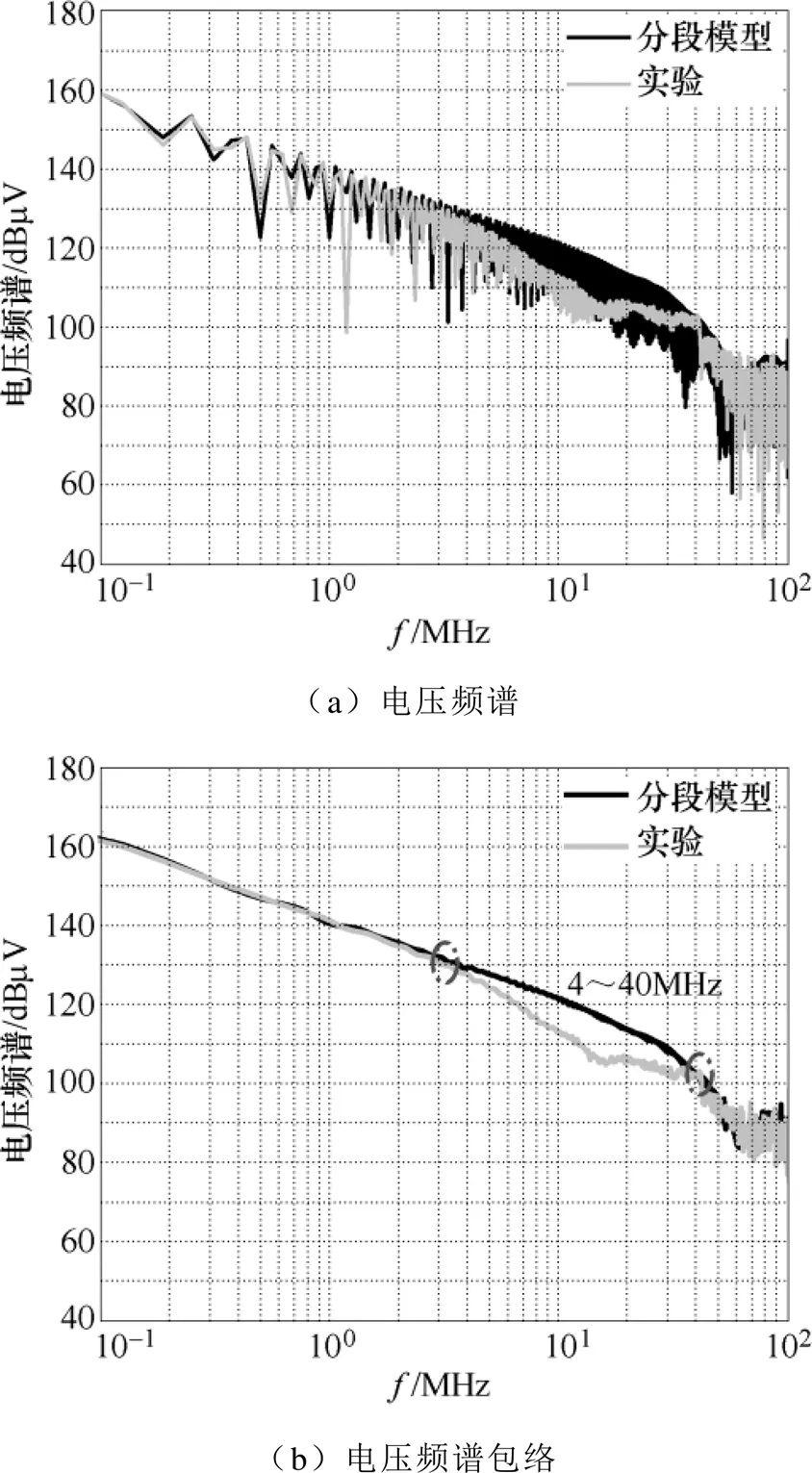
图11 实验和分段模型的电压频谱对比
由式(18)可知,关断过程电压的上升斜率与gc成反比关系。根据图6所示的电容测量结果,gc在0~200V范围内变化较大,将gc等效为两个离散电容的建模方法准确度不够。因此,考虑在0~200V范围内增加gc模型的分段数量,由多阶电容组成gc等效模型,如图12所示。将图6的等效电容定义为“二段等效模型”。图12给出了gc的二段、三段及四段等效模型示意图,分别由2、3和4个离散电容组成。图13对比了不同复杂程度的gc等效模型对应的电压频谱。与二段模型相比,gc三段等效模型在20~40MHz范围内的预测准确度有显著提高,与实验波形频谱差异很小,在4~20MHz的误差也缩小到5dB左右。gc四段等效模型进一步缩小了电压模型与实际波形频谱在4~20MHz范围内的差异。
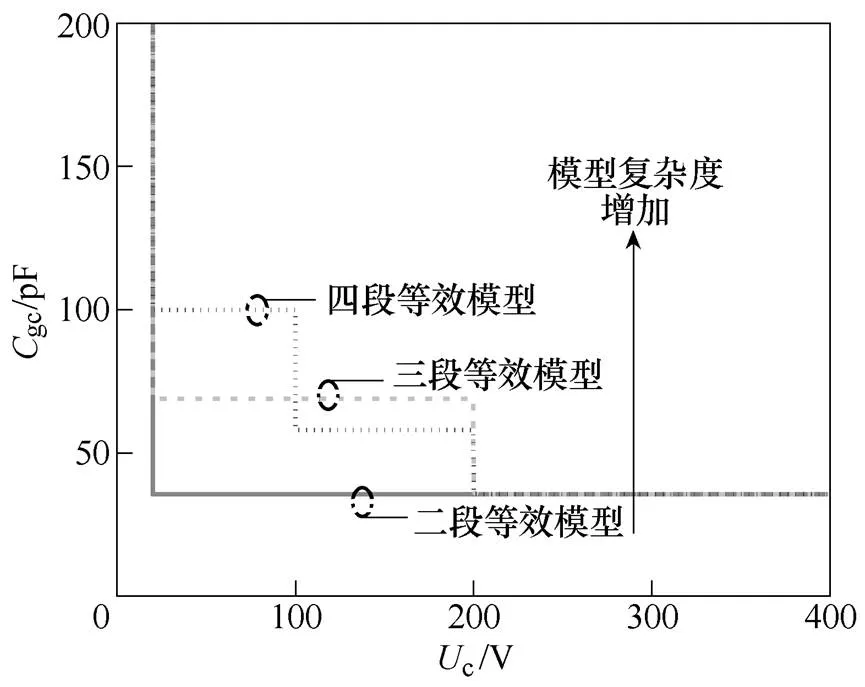
图12 不同分段数的Cgc等效模型
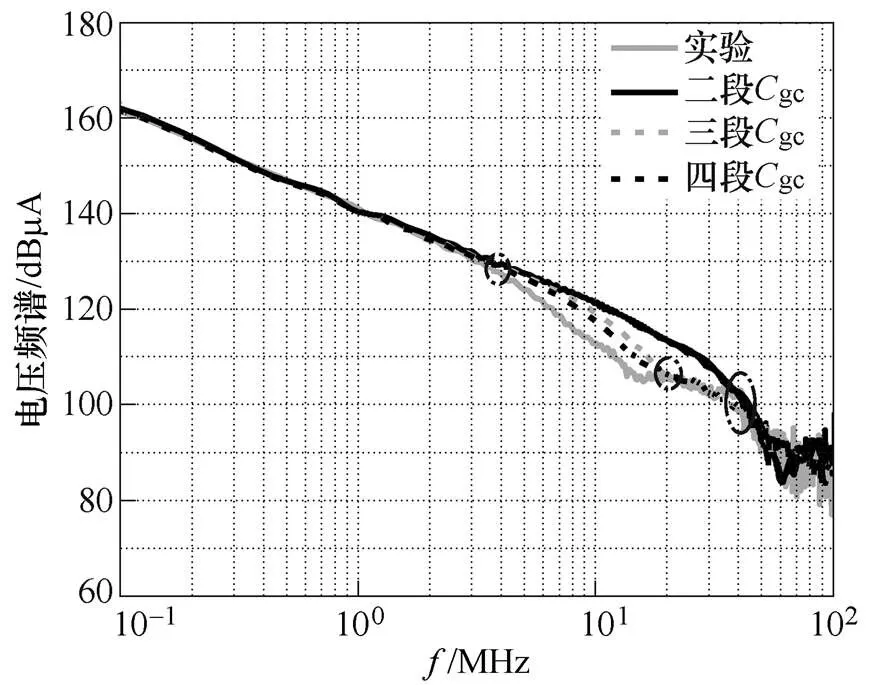
图13 不同Cgc等效模型下的电压频谱对比
对于gc的三段和四段模型,本文是通过实测获取gc随器件电压的变化曲线,在电容值变化最显著的电压范围内进行分段处理,分段临界电压和电容值具有随机性,但也证明了gc多阶模型的方法可以显著提高模型的精度。后续可以通过深入分析gc多阶模型的分段方法来实现模型精度的最优化。综合考虑模型的复杂度与EMI预测的准确度,本文建议采用三段gc等效模型。需要注意的是,开关电流的暂态变化主要受ge的影响,因此电流频谱特性与gc模型阶数的关联性很小,电流分段模型不需要考虑gc多阶模型。
5 结论
IGBT暂态过程的d/d和d/d是影响实际换流器EMI水平的关键因素,IGBT开关电压和电流波形的频谱特性可以进一步用于换流器EMI水平的评估。本文建立了考虑寄生振荡的IGBT分段暂态模型,分阶段计算了暂态电流和电压的变化率,考虑了器件的非线性电容和寄生参数对各阶段d/d和d/d的影响。为了验证上述模型对波形频谱的预测结果,搭建了二极管钳位感性负载测试平台,对测试平台的寄生参数和器件参数进行提取,分析对比了电压电流模型和实验波形的频谱特性。本文提出的IGBT分段模型提高了对实际波形频谱特性预测的准确度。
分段电流模型与IGBT实际电流波形的频谱差异很小,能够较好地预测电流干扰源相关的EMI特性。IGBT开通过程中的电流振荡现象会导致电流频谱在振荡频点处出现峰值。考虑振荡过程的电流模型可以更好地对振荡引入的EMI峰值进行预判。
分段电压模型能够较好地预测IGBT实际电压波形的频谱特性,但在特定频段出现部分差异,这主要是由gc等效模型的误差造成的。建立多阶gc模型,在不同电压范围采用多个离散电容来等效gc,可以显著提高电压模型对实际电压波形频谱的预测准确度。由于增加gc模型的分段数量也提高了模型的复杂程度,通过对比不同gc模型下电压模型与实际波形的频谱差异,建议采用三段gc等效模型。
本文基于开关等效电路建立IGBT的分段电压和电流模型也适用于MOSFET器件。通过进一步完善本文模型,可用于分析具有更快的开关速度能力和剧烈寄生振荡现象的SiC MOSFET相关EMI问题。
[1] 钱照明, 张明军, 盛况. 电力电子器件及其应用的现状和发展[J]. 中国电机工程学报, 2014, 34(29): 5149-5161.
Qian Zhaoming, Zhang Mingjun, Sheng Kuang. Status and development of power semiconductor devices and its applications[J]. Proceedings of the CESS, 2014, 34(29): 5149-5161.
[2] 王希平, 李志刚, 姚芳. 模块化多电平换流阀IGBT器件功率损耗计算与结温探测[J]. 电工技术学报, 2019, 34(8): 1636-1646.
Wang Xiping, Li Zhigang, Yao Fang. Power loss calculation and junction temperature detection of IGBT devices for modular multilevel valve[J]. Transactions of China Electrotechnical Society, 2019, 34(8): 1636-1646.
[3] 王兴贵, 薛晟, 李晓英. 模块化多电平变流器半桥串联结构微电网输出特性分析[J]. 电工技术学报, 2019, 34(10): 2130-2140.
Wang Xinggui, Xue Sheng, Li Xiaoying. Analysis of output characteristics of a microgrid based on modular multilevel converter half-bridge series structure[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2130-2140.
[4] He Jiangbiao, Yang Qichen, Wang Zheng. On-line fault diagnosis and fault-tolerant operation of modular multilevel converters: a comprehensive review[J]. CES Transactions on Electrical Machines and Systems, 2020, 4(4): 360-372.
[5] 孙帆, 王金梅, 鲁娅楠. 模块化多电平变流器改进最近电平调制策略的研究[J]. 电气技术, 2019, 20(2): 23-27.
Sun Fan, Wang Jinmei, Lu Yanan. Research on improved nearest level modulation strategy for modular multilevel converter[J]. Electrical Engineering, 2019, 20(2): 23-27.
[6] 王一凡, 赵成勇, 郭春义. 双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J]. 电工技术学报, 2019, 34(10): 2116-2129.
Wang Yifan, Zhao Chengyong, Guo Chunyi. Small signal stability and oscillation suppression method for islanded double fed induction generator-based wind farm integrated by modular multilevel converter based HVDC system[J]. Transactions of China Elec- trotechnical Society, 2019, 34(10): 2116-2129.
[7] 孙海峰, 杜林森, 梁贵书. 模块化多电平换流阀系统天线模型及其辐射电磁骚扰特性分析[J]. 中国电机工程学报, 2016, 36(3): 879-888.
Sun Haifeng, Du Linsen, Liang Guishu. Antenna model of MMC-HVDC converter valve system and its radiated electromagnetic disturbance analysis[J]. Proceedings of the CESS, 2016, 36(3): 879-888.
[8] 郭彦杰, 王丽芳, 廖承林. 电动汽车用IGBT及逆变器的电磁兼容性分析[J]. 高电压技术, 2014, 40(6): 1732-1737.
Guo Yanjie, Wang Lifang, Liao Chenglin. Analysis of EMC characteristics on IGBT and inverter in electric vehicles[J]. High Voltage Engineering, 2014, 40(6): 1732-1737.
[9] 钱照明, 陈恒林. 电力电子装置电磁兼容研究最新进展[J]. 电工技术学报, 2007, 22(7): 1-11.
Qian Zhaoming, Chen Henglin. State of art of electro- magnetic compatibility research on power electronic equipment[J]. Transactions of China Electrotechnical Society, 2007, 22(7): 1-11.
[10] 杜晓磊, 郭庆雷, 吴延坤, 等. 张北柔性直流电网示范工程控制系统架构及协调控制策略研究[J]. 电力系统保护与控制, 2020, 48(9): 164-173.
Du Xiaolei, Guo Qinglei, Wu Yankun, et al. Research on control system structure and coordination control strategy for Zhangbei demonstration project of MMC-HVDC grid[J]. Power System Protection and Control, 2020, 48(9): 164-173.
[11] Zhang Jian, Lu Tiebing, Zhang Weidong, et al. Characteristics and influence factors of radiated disturbance induced by IGBT switching[J]. IEEE Transactions on Power Electronics, 2019, 34(12): 11833-11842.
[12] Gong Xun, Ferreira J A. Comparison and reduction of conducted EMI in SiC JFET and Si IGBT-based motor drives[J]. IEEE Transactions on Power Electro- nics, 2014, 29(4): 1757-1767.
[13] Consoli A, Musumeci S, Oriti G, et al. An innovative EMI reduction design technique in power con- verters[J]. IEEE Transactions on Electromagnetic Compatibility, 1996, 38(4): 567-575.
[14] 曹勇, 杨飞, 李春晖, 等. 不同耦合系数下的交错并联电流连续模式Boost功率因数校正变换器的传导电磁干扰[J]. 电工技术学报, 2019, 34(10): 2176- 2186.
Cao Yong, Yang Fei, Li Chunhui, et al. Conducted electromagnetic interference of interleaved continuous current mode boost power factor correction converter with different coupling coefficients[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2176-2186.
[15] 江师齐, 刘艺涛, 银杉, 等. 基于噪声源阻抗提取的单相逆变器电磁干扰滤波器的设计[J]. 电工技术学报, 2019, 34(17): 3552-3562.
Jiang Shiqi, Liu Yitao, Yin Shan, et al. Electro- magnetic interference filter design of single-phase inverter based on the noise source impedance extraction[J]. Transactions of China Electrotechnical Society, 2019, 34(17): 3552-3562.
[16] 孟进, 马伟明, 张磊, 等. 变换器传导电磁干扰集中等效模型参数估计方法[J]. 电工技术学报, 2005, 20(6): 25-29.
Ma Jin, Ma Weiming, Zhang Lei, et al. Parameter estimation of lumped circuit models for conducted EMI in power converters[J]. Transactions of China Electrotechnical Society, 2005, 20(6): 25-29.
[17] 肖芳, 孙力. 功率变换器IGBT开关模块的传导电磁干扰预测[J]. 中国电机工程学报, 2012, 32(33): 157-164.
Xiao Fang, Sun Li. Predicting conducted electro- magnetic interference for IGBT switching module in power converter systems[J]. Proceedings of the CESS, 2012, 32(33): 157-164.
[18] Meng Jin, Ma Weiming, Pan Qijun, et al. Multiple slope switching waveform approximation to improve conducted EMI spectral analysis of power con- verters[J]. IEEE Transactions on Electromagnetic Compatibility, 2006, 48(4): 742-751.
[19] Yang Xin, Yuan Ye, Zhang Xueqiang, et al. Shaping high-power IGBT switching transitions by active voltage control for reduced EMI generation[J]. IEEE Transactions on Industry Applications, 2015, 51(2): 1669-1677.
[20] Yang Xin, Long Zhiqiang, Wen Yanhui, et al. Investigation of the trade-off between switching losses and EMI generation in Gaussian S-shaping for high-power IGBT switching transients by active voltage control[J]. IET Power Electronics, 2016, 9(9): 1979-1984.
[21] Oswald N, Stark B H, Holliday D, et al. Analysis of shaped pulse transitions in power electronic switching waveforms for reduced EMI generation[J]. IEEE Transactions on Industry Applications, 2011, 47(5): 2154-2165.
[22] 蒋有缘, 陈萍, 刘文苑, 等. 基于IGBT的Buck电路共模EMI特性研究[J]. 高电压技术, 2008, 34(10): 2234-2239.
Jiang Youyuan, Chen Ping, Liu Wenyuan, et al. Common-mode EMI behavior of an IGBT Buck converter[J]. High Voltage Engineering, 2008, 34(10): 2234-2239.
[23] 徐晓贤, 沙广林, 庄园, 等. IGBT模块的新型开关模型与损耗分析[J]. 电源学报, 2018, 16(6): 152-158.
Xu Xiaoxian, Sha Guanglin, Zhuang Yuan, et al. Model and loss analysis of novel switching of IGBT modules[J]. Journal of Power Supply, 2018, 16(6): 152-158.
[24] 邓夷, 赵争鸣, 袁立强, 等. 适用于复杂电路分析的IGBT模型[J]. 中国电机工程学报, 2010, 30(9): 1-7.
Deng Yi, Zhao Zhengming, Yuan Liqiang, et al. IGBT model for analysis of complicated circuits[J]. Pro- ceedings of the CESS, 2010, 30(9): 1-7.
[25] 沈卓轩, 姜齐荣. 电力系统电磁暂态仿真IGBT详细建模及应用[J]. 电力系统自动化, 2020, 44(2): 235-247.
Shen Zhuoxuan, Jiang Qirong. Detailed IGBT mode- ling and applications of electromagnetic transient simulation in power system[J]. Automation of Electric Power Systems, 2020, 44(2): 235-247.
[26] 陈玉林, 孙驰, 艾胜, 等. 一种中电压大功率IGBT模块行为模型[J]. 电工技术学报, 2017, 32(4): 25-34.
Chen Yulin, Sun Chi, Ai Sheng, et al. The medium- voltage high power IGBT module behavior model[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 25-34.
[27] Wang Jianjing, Chung S H, Li T H. Characterization and experimental assessment of the effects of parasitic elements on the MOSFET switching perfor- mance[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 573-590.
[28] 谢宗奎, 柯俊吉, 赵志斌, 等. 碳化硅MOSFET换流回路杂散电感提取方法的优化[J]. 电工技术学报, 2018, 33(21): 4919-4927.
Xie Zongkui, Ke Junji, Zhao Zhibin, et al. Optimized extraction method of stray inductance in commutation path for silicon carbide MOSFET[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 4919- 4927.
[29] Oswald N, Anthony P, McNeill N, et al. An experi- mental investigation of the tradeoff between switching losses and EMI generation with hard-switched all-Si, Si-SiC, and all-SiC device combinations[J]. IEEE Transactions on Power Electronics, 2014, 29(5): 2393-2407.
Analysis of the Influence of IGBT Segmented Transient Model with Parasitic Oscillation on Electromagnetic Interference Prediction
1121
(1. State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources North China Electric Power University Beijing 102206 China 2. Fujian Electrical Power Research Institute Fuzhou 350003 China)
The d/dand d/dof the insulated gate bipolar transistor (IGBT) switching process are the major factors affecting the electromagnetic interference (EMI) level of the converter. The parasitic oscillation of IGBT is an important part of high frequency EMI, and the EMI peak appears at the oscillation frequency. In this paper, an IGBT segmented transient model considering parasitic oscillations was presented. The effects of parasitic parameters and device nonlinear capacitance on switching characteristics were analyzed. The voltage and current change rates at different stages were calculated respectively. Then, a diode-clamped inductive load test platform was built. The current and voltage waveforms of IGBT were obtained, and the spectrum characteristics of the segmented model and the actual waveform were analyzed and compared. Finally, it is verified through experiments that the oscillation process in the model is the key factor affecting the current spectrum characteristics, and the three-stage equivalent model ofgccan significantly improve the accuracy of voltage spectrum prediction. The proposed model improves the prediction accuracy of the IGBT interference source spectrum and can be used to evaluate the EMI level of the actual converter.
Insulated gate bipolar transistor (IGBT), segmented transient model, parasitic oscillations, spectrum
TM46
10.19595/j.cnki.1000-6753.tces.201416
国家电网公司科技资助项目(52130419000M)。
2020-10-26
2021-02-03
黄华震 男,1995年生,博士研究生,研究方向为电力电子器件的EMI特性。E-mail: huazhenhuang@ncepu.edu.cn
卢铁兵 男,1970年生,教授,博士生导师,研究方向为先进输变电技术、IGBT及电力系统的电磁兼容。E-mail: tiebinglu@ncepu.edu.cn(通信作者)
(编辑 陈 诚)

