一种新的倍立方体尺规构图方法

何怀福

（新疆风能研究所有限责任公司，新疆 乌鲁木齐 830000）

一、概述

英国科学哲学家卡尔·波普尔（Karl Popper，1902 — 1994）认为，知识是通过猜想（Conjecture）和反驳（Refutation）而进步的[4]。古希腊哲学家 柏拉图（Plato，427 B.C —347 B.C）主张通过学习几何，可以培养逻辑思维能力。《原本》（Elements）是古希腊数学家欧几里得（Euclid，325 BC—265 BC）所著，它是一部古典几何的奠基之作，开创了数学公理化体系结构，构建出一座演绎几何的宏伟大厦[1]。我国明代数学家徐光启将欧氏《原本》译成中文后，并定名为《几何原本》，沿用至今。

公元前五世纪，在古希腊雅典城内诞生一个“巧辩学派”（Sophist，又称为智人学派，或诡辩学派），该学派提出了『尺规构图』的三大几何问题，即三等分角、倍立方体和化圆为方等。尺规构图（Straightedge and Compass Constructions，又译为尺规作图）是由古希腊数学家伊诺皮迪斯（Oenopides of Chios，约 490 B.C—420 B.C）最先提出来的，后来在《几何原本》中用公设的形式固化下来，于是，尺规构图就成为希腊古典几何的金科玉律。将现实中的尺规构图问题抽象为数学上的约定，称之为尺规构图公法。

在三大几何难题提出后的两千余年中，曾有众多的尝试，但没有人能够给出严格的答案。随着十九世纪群论的发展，德国数学家林德曼（Lindemann，1852—1939）和·克莱茵（F·Kiein，1849—1925）分别证明了三大几何难题用尺规构图的不可能性。从代数的角度来看，好像彻底解决了这些悬案[3]。但从不同的视角来看，这些问题也许能得到不同的答案，在下一节提供一种新的倍立方体尺规作图方法，将为您打开一扇几何思维之窗。

二、一种新的倍立方体尺规作图方法

倍立方体问题的完整叙述如下。

假设任意给定一个线段（a），是否能够通过尺规构图，在有限次内作出另一个线段（b），使以该线段（b）为边长的立方体的体积是以给定线段（a）为边长的立方体的体积的2倍（即b3=2a3）？

英国数学家怀特海（Alfred North Whitehead，1861—1947）指出，获取知识的前提是不受知识的束缚[5]。倍立方体（Doubling the Cube）是一个非常古老的几何问题。虽然，德国数学家林德曼（Lindemann）和克莱茵（F·Kiein）证明了三大几何难题用尺规构图的不可能性。但是，如果换个视角来描述『倍立方体』问题，就会得到不同的结果。

转换一下思维视角，倍立方体问题新的叙述如下。

如果将给定线段的长度设为单位长度1（即a=1），则倍立方问题就转化成，作出一个长度为（即b=1+x）的线段，使得（1+x）3=2方程成立，则倍立方体问题就能得到解决。

已知：以单位长度为边长的立方体。

求作：作一新立方体的体积是已知立方体的2倍。

作图：见2.2节。

证明：见2.3节。

2.1 倍立方体之新解法思路

根据前面有关倍立方体问题新的叙述方法，将（1+x）3=2方程再转换一下形式，就能得到期望的结果。

倍立方体之新解法思路概述如下：

再将[式①]左边展开，得到下式：

1+3sinφ+3sin2φ+sin3φ=2，简化后得：

然后，将[式②]整理后得到下式：

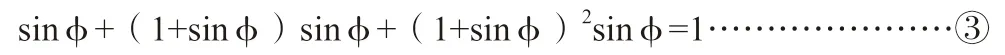
从[式③]得到的启发：关键是通过尺规构图找到满足[式③]的角度φ（此φ可称之为倍立方体角），通过降维思考，倍立方体问题就能得到完满解决。

2.2 倍立方体：尺规构图步骤

倍立方体尺规构图步骤列示如下。

第一步，以[点O]作为中心点，分别作[横轴OX]和[纵轴OY]（公设I.1[1]）（见图2.2.1）。

第二步，取给定的长度（或合适的长度）OA作为[单位一]（定义VII.1[1]）。用该[单位一]作为圆的半径，作[单位圆ABC]（公设I.3[1]）（见图2.2.1），其中：点O为单位圆ABC的圆心（定义I.16）。

第三步，以[点O]为圆心，取OA的2倍长度OD（公理 I.2[1]）作为圆的半径，作[圆DEF]（公设I.3[1]）（见图2.2.1）。

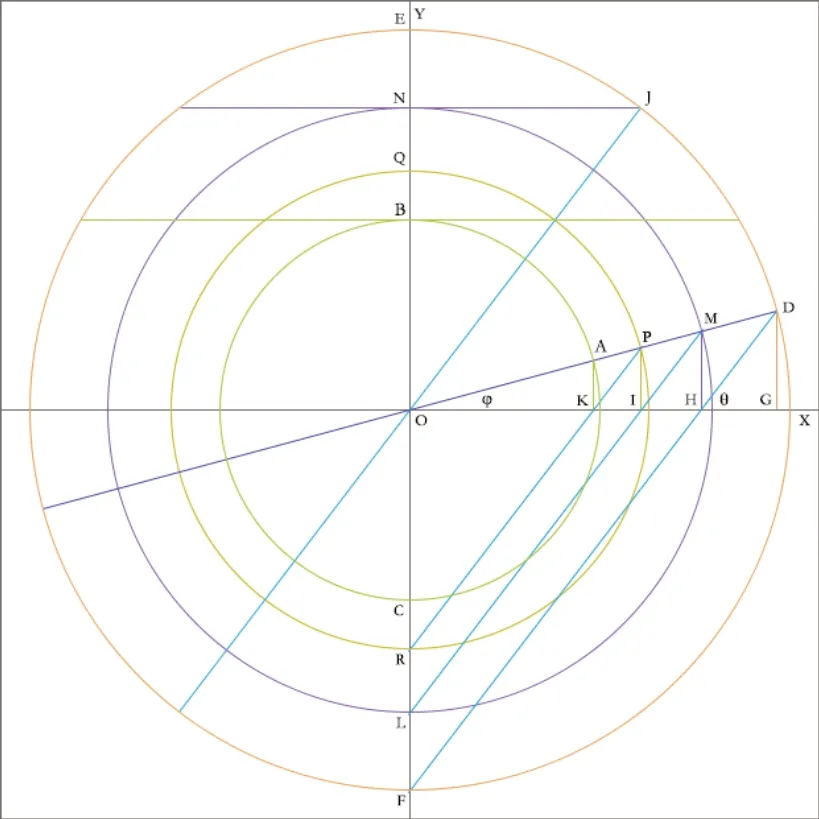
图2.2.1 ∠DOG= φ（倍立方体角）

第四步，连接F、D两点，作一斜线FD（公设I.1[1]）与[横轴OX]相交于[点H]，该直线延长后与[圆DEF]相交于[点D]（见图2.2.1）。

第五步，连接O、D两点，作一斜线OD（公设I.1[1]）（见图2.2.1）。第六步（可选，供证明时使用），经过[横轴OX]外的D点，作[垂线DG]（命题I.12[1]），并与[横轴OX]相交于[点G]（见图 2.2.1）。

第七步，过[横轴OX]上的[点H]，作垂线MH（命题I.11[1]），与斜线OD相交于[点M]（见图2.2.1）。

第八步，以[点O]为圆心，以长度OM作为圆的半径，作[圆MNL]（公设I.3[1]），并与[纵轴]分别相交于[点N]和[点L]（见图2.2.1）。

第九步，过[点N]作一与[横轴]平行的平行线NJ（命题 I.31[1]），并与[圆DEF]相交于[点J]（见图2.2.1）。

第十步，连接O、J两点，作一斜线OJ（公设I.1[1]），使得角JOG与角DHG相等（命题I.23）（见图2.2.1）。

第十一步，连接L、M两点，作一斜线LM（公设I.1[1]）与[横轴OX]相交于[点I]（见图2.2.1）。

第十二步，过[横轴OX]上的[点I]，作垂线PI（命题I.11[1]），与斜线OD相交于[点P]（见图2.2.1）。

第十三步，以[点O]为圆心，以长度OP作为圆的半径，作[圆PQR]（公设 I.3[1]），并与[纵轴]分别相交于[点Q]和[点R]（见图2.2.1）。

第十四步，连接P、R两点，作一斜线PR（公设I.1[1]）与[横轴OX]相交于[点K]（见图2.2.1）。

第十五步（可选，供证明时使用），过[横轴OX]上的[点K]，作垂线AK（命题I.11[1]），与斜线OD相交于[点A]（见图2.2.1）。

第十六步，以长度OP为边，作一正六边形（即立方体）（定义XI.25[1]）。该立方体之体积等于以长度OA为边的立方体之体积的2倍。

至此，完成『倍立方体』作图步骤，在下一节可以看到证明过程。作完（Q.E.F）

2.3 倍立方体：证明过程

如果说点、线、面是“欧氏几何”之基本要素，那么圆则是开启几何世界宝库之密钥，圆也是最完满和最具魔力的图形。

通过尺规构图，找到倍立方体角φ后，就能完成倍立方体作图任务。在本小节，给出证明“第2.2节”倍立方体尺规构图操作的正确性。

为了方便演算，假设：

（1）角∠DOG值记为φ，即∠DOG=φ。

（2）角∠DHG值记为θ，即∠DHG=θ，经简单推算得到：

θ=（π/4+φ/2）。

首先，在[图2.2.1]中，根据“对顶角相等”（命题I.15[1]），得到：

∠OHF=∠DHG=θ。

在直角三角形△FOH中，得到：

∠OFH=π/2﹣∠OHF=π/2﹣θ。

在[圆DEF]中，由OD=OF（定义I.15[1]），得到三角形△DOF 是等腰三角形（定义I.20[1]）。根据“等腰三角形两底角相等”（命题I.5[1]），得到：

∠ODF=∠OFD，等价于：

∠ODH=∠OFH =π/2﹣θ。

由[图2.2.1]得知，∠DOH=∠DOG=φ。

而且，角∠DHG是三角形△DOH的一个外角，根据“三角形一个外角等于两个内角和”（命题I.32[1]），得到：

∠DHG=∠DOH+∠ODH，即：

θ=φ+（π/2﹣θ），化简后得到：

θ=π/4 +φ/2。

根据三角函数加法公式，由sinθ=sin（π/4+φ/2），得到：

sinθ=sin（π/4）cos（φ/2）+cos（π/4）sin（φ/2），即：

sinθ=（cos（φ/2）+sin（φ/2））/（√（2）），等式两边取平方，推得：

详细证明步骤列示如下：

第一步，参看[图2.2.1]，在三角形△DMH中：

∠MDH=∠ODH=π/2﹣θ=π/4-φ/2，以及：

∠MHD=π/2﹣∠DHG=π/2﹣θ=π/4–φ/2，得到：

∠MHD=∠MDH。

根据“等角对等边”（命题 I.6[1]），得到：

MD=MH。

在[图2.2.1]中，有MD=OD﹣OM，和MH=OM×sinφ，代入上式得到：

OD﹣OM=OM×sinφ，

根据“第2.2节第三步”操作得到，OD 是[圆DEF]的半径，即：

OD=2，代入上式得到：

2﹣OM=OM×sinφ，化简后得到：

第二步，根据“第2.2节第十步”操作得到，角∠JOG与角∠DHG相等，即：

∠JOG=∠DHG=θ。

在[图2.2.1]中，有：

OJ×sinθ=ON，

由于，ON是[圆MNL]的半径，有ON=OM（定义I.15[1]），得到：

OJ×sinθ = OM。

再根据“第2.2节第三步”操作，得到OJ=OD=2（定义I.15[1]），并将[式②]代入上式，得到：

2sinθ=2/（1+sinφ），化简后得到：

sinθ=1/（1+sinφ），两边取平方，得到：

sin2θ=[1/（1+sinφ）]2，

再将[式①]代入上式，得到：

（1+sinφ）/2=[1/（1+sinφ）]2，化简后得到：

此处说明，该角φ对应“第2.1节”中描述的倍立方体角。

第三步，在[图2.2.1]中，由“第2.2节第六步、第十二步、第十五步”操作得知，根据“若两角对应相等（或三个角分别对应相等），则两个三角形相似”判定定理得到：直角三角形Rt△DOG、Rt△MOH、Rt△POI、Rt△AOK彼此相似，即：

△DOG∽△MOH∽△POI∽△AOK。

根据“相似三角形对应边成比例”，则有：

DG：MH=OG：OH OD：OM=OH：OI=MH：PI，

由DG：MH=MH：PI，得到：

类似地，MH：PI=OH：OI=OM：OP=OI：OK=PI：AK，

由MH：PI=PI：AK，得到：

PI2=MH×AK，

将上式代入[式④]，得到：

转换[式⑤]，得到：

第四步，在[图2.2.1]中，根据“第2.2节第七步”操作，得到：

MH=OM×sinφ，

并将[式②]代入上式，得到：

MH=OM×sinφ=2sinφ/（1+sinφ），

DG=OD×sinφ=2sinφ，

分别将MH和DG代入[式⑥]，得到：

AK=[2sinφ/（1+sinφ）]3/（2sinφ）2，即：

AK=2sinφ）/（1+sinφ）3

再将[式③]代入上式，得到：

AK=（2sinφ）/2，化简后得到：

AK=sinφ。

此处说明，[点A]就是斜线OD与[单位圆ABC]的相交点。

第五步，在[图2.2.1]中，根据“第2.2节第十一步”操作，得知OM和OL均是[圆MNL]的半径，得到：OM=OL（定义I.15[1]），故三角形△MOL是等腰三角形（定义I.20[1]）。根据“等腰三角形两底角相等”（命题I.5[1]），得到：

∠OML=∠OLM。

经过简单推算，得到：

∠MIH=（π/4+φ/2），等价于：

∠MIH=∠DHG=θ。

根据“内错角相等两直线平行”的判定定理（命题I.28[1]）得到：

LM与FD平行，即：

LM//FD。

类似地，通过递推也能得到：

∠PKI=（π/4+φ/2），等价于：

∠PKI=∠MIH=∠DHG=θ，

类似得到RP与LM和FD平行（命题I.28[1]），即：

RP//LM//FD。

由于，∠OPR=∠ORP=π/2﹣∠PKI，

∠OPR=π/2﹣（π/4+φ/2），即：

∠OPR=π/4﹣φ/2。

而，∠AKP=π/2﹣∠PKI，同样得到：

∠AKP=π/4﹣φ/2。

由此得到，三角形△PAK是等腰三角形，即：

AP=A=sinφ。

第六步，根据“第 2.2 节 第二步”操作，得到OA是[单位圆ABC]半径，即：

OA = 1。

在[图2.2.1]中，有 OP = OA + AP，即：

OP = 1+sinφ。

由此得到，以长度OP（即 1+sinφ）为边作一正六边形（即立方体），其体积正好等于以单位长度OA为边的立方体体积的两倍。

故“第 2.2 节”操作正确性已得到证明。

证完（Q.E.D）

结语

英国哲学家怀特海（Whitehead）认为，我们的知识体系应该保持开放[5]。在欧几里得几何空间里，直线和圆形是最基本、最完美的几何图形；而在易经思维世界，方形和圆形才是最完美的图形，也是最基本的抽象思维信元。本文汲取了东西方伟人们的卓越智慧和思想[2]，通过体悟、领悟和觉悟等三个层次的深度修炼达到一个全新的思维境界。

现仍传世的《欧几里得几何原本》（Euclid’s Elements）震撼我们的精神世界和滋润我们的心灵已有两千多年了。在古希腊雅典“巧辩学派”提出尺规构图的三大几何问题后，激活众多数学和几何天才们的智慧源泉，完善了几何演绎体系，牢固了几何神殿之基础。

如果说点、线、面是欧氏几何之基本要素，那么圆则是开启几何世界宝库之密钥。圆也是最具魔力和最完美的图形。在本文中提供的倍立方体之新解法打开了几何世界的一扇窗，打破了代数方法在几何世界的垄断地位，在追求真理的路途中充分放飞了思维的想象力和创造力，让传统的几何方法焕发了新的生命力。