基于solidworks simulation的结构受压的变化及优化方式

陈军

摘 要：在工业结构中，经常遇到横截面加筋的问题，也就是如何合理的设计出一种类型的筋板使得整体结构受力更加均匀，最大应力更小，变形更小，我们将此类的优化统称为机械优化设计。机械优化设计是一门非常重要的学科，在机械工程中具有非常重要的应用价值.现代技术的飞速发展，尤其是计算机技术的进步，推动了机械工程中的设计方法和技术创新的发展[1]。本文讲述了通过solidworks simulation的优化并分析，得出较为合理的截面形状。

关键词：结构优化、体积与质量角度、solidworks simulation

有限元法是将连续体离散化，通过对有限个单元作分片插值求解各种力学、物理问题的一种数值方法。有限元法把连续体离散成有限个单元，单个单元的场函数是只包含有限个待定节点参量的简单场函数，这些单元场函数的集合就能近似代表整个连续体的场函数。根据能量方程或加权参数方程可建立有限个待定参量的代数方程组，求解此离散方程组就得到有限元法的数值解。有限元法已被用于求解线性和非线性问题，并建立了各种有限元模型[2]。

solidworks simulation是达索公司旗下子公司的SolidWorks产品中的一个优化设计模块，运用了有限元分析原理，通过软件设计编程，实现了计算机自动计算。在有限元分析中涉及到了大量的复杂的计算，需要深厚的数学功底，花费巨量的时间才能计算出结果，并且计算的过程中非常容易出错，而通过solidworks simulation模块，可以快速模拟受力情况，并根据现有的情况进行计算机自动分析，这样就可以使一般的工程技术人员，通过短期的培训就能够进行产品分析，并且快速的得到相应的计算结果，然后再通过计算结果进行相应的分析，不断地优化迭代，形成最终产品结构，极大的缩短的研发周期，降低的设计成本，提高的产品设备的质量，从而可以给公司带来更大的利益。

1、从占用体积的角度分析结构强度

在很多结构设计中会遇到加强筋的设计，在外形一定的空腔中加入一定的筋结构，使得结构的抗压能力更高。这种情况下，结构的外形并没有发生改变，整体的强度得到了增强，但是不同形式的加强筋可以得到不同强度的结构。一般情况下，设计人员是希望强度能够约高约好，而外形体积不变，这个时候，我们可以通过在内部增添各种形式的筋板，再通过solidworks simulation进行有限元分析分别得出不同形式下的结构强度结果，最后进行对比选择，选出较优解。

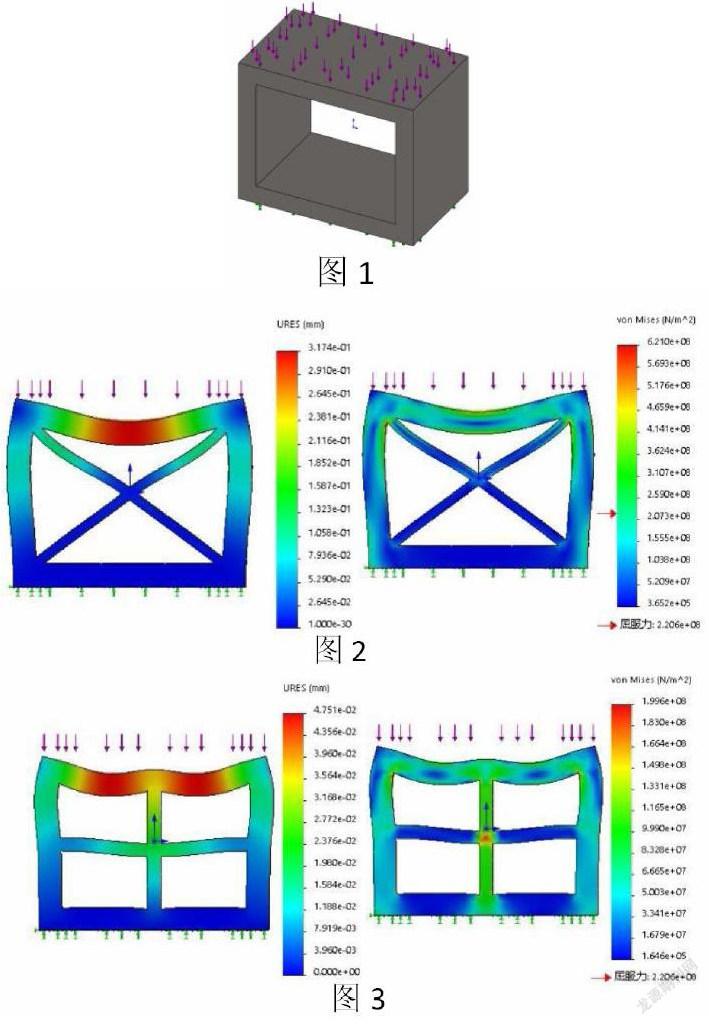
在图1中可见一口子型截面，底面为固定面，上表面受均布正压力，此时在其内部增加加强筋，使得整体结构受力更加均匀，最大应力更小，变形更小。可以从机床设计手册和机械设计手冊中得出内部加筋有叉字型（图2）、十字型（图3）、米字型（图4）、太阳型（图5）这四类常用类型，结论中说明太阳型优于米字型、米字型优于其他两型。其实也很好理解，从截面图上看，不考虑模型的厚度时，太阳型的交点最多，米字型其次，其余两型较少，所以交点较多的截面将所受到的力逐步分摊出去，故结构受力更加均匀，最大应力更小，变形更小。

仅仅从占用体积的角度分析，如果这四类形式的加强筋厚度相同，那么这四种类型的占用体积是一致的，即在设备中占用的空间一样，但它们的质量是太阳型重于米字型、米字型重于其他两型。当所设计的设备不考虑质量影响时，那么结构的刚度K和应力σ依然是太阳型优于米字型、米字型优于其他两型。

2、从占用体积与质量的双角度分析结构强度

在第1条中，我们考虑了通过加强筋去强化外形一定的空腔结构，从上述结果中，可以清晰的分析出此时结构的强度确确实实得到了极大的提高，但是设计人员会发现每一种添加加强筋后的结构的质量也是各不相同。在很多时候，我们非常在乎设备质量的情况下，如在有额定载荷要求的楼层或设备底层结构不允许超过一定载荷，那么第1条中所涉及的优化方式并不一定适合，此时，我们需要从体积与质量这两个角度去进行分析，我们依然是通过solidworks simulation进行有限元分析，在不超过任务书中要求的质量的情况下，得到不同形式下的结果，再通过结果中显示出的低强度位置，合理分配加强筋到各个薄弱部位，将筋板质量尽量增加到薄弱位置，减少或去除非薄弱位置的筋板质量，此消彼长地去优化设计空腔内的结构，最终可以得到收敛解，即为较优解。

当我们从体积与质量这两个角度去分析时，如果这四类形式的加强筋厚度相同，占用体积也相同，但刚度与质量的比值K/m（即K表示刚度，m表示质量），就很难判断出哪种类型的K/m值更高。在一般情况下，质量越大，刚性也会越大，所以如果在一个设备中，设备是比较重视质量，那么这个K/m值就不容忽视。

我们通过控制变量法，改变这四种类型的加强筋厚度，使得这四种类型的截面模型质量相等，我们分别来分析一下他们的刚度K和应力σ。

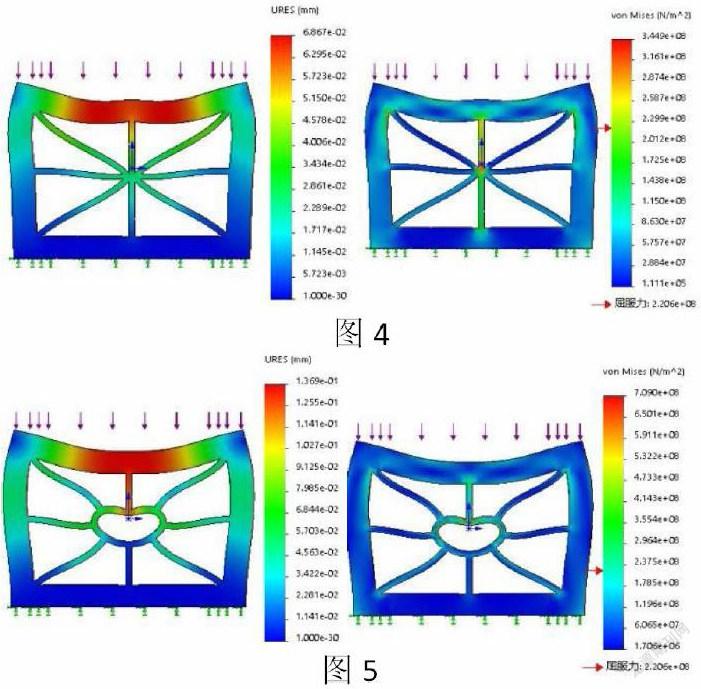
第一种是叉字型，进过solidwork simulation有限元软件分析，如图2得，最大变形量在上表面中间位置，为0.32mm，而最大应力在左上角和右上角处，为621Mpa。

第二种是十字型，进过有限元软件分析，如图3得，最大变形量在上表面的三分之一位置，为0.05mm，而最大应力在截面中间处，为199Mpa。

第三种是米字型，进过有限元软件分析，如图4得，最大变形量在上表面中间略偏两侧位置，为0.07mm，而最大应力在截面中间处，为345Mpa。

第四种是太阳型，进过有限元软件分析，如图5得，最大变形量在上表面中间略偏两侧位置，为0.14mm，而最大应力在截面中间处，为709Mpa。

从上面的四种情况来看，相同质量的筋板的情况下，太阳型是刚性最差的，而十字型是刚性最好的。可以看出如果我们按照原有理论照搬，会出现严重的错误，因为需要控制质量不变，那么筋的截面积需要相等，越复杂的截面，筋便会越多，会导致筋的厚度减小，从而导致强度降低。

3、从占用体积与质量的双角度优化结构强度

此时，可以通过第2条中的讲述的减少或去除非薄弱位置的筋板质量，增添薄弱位置的筋板质量来提高腔体强度，并保持质量不变。

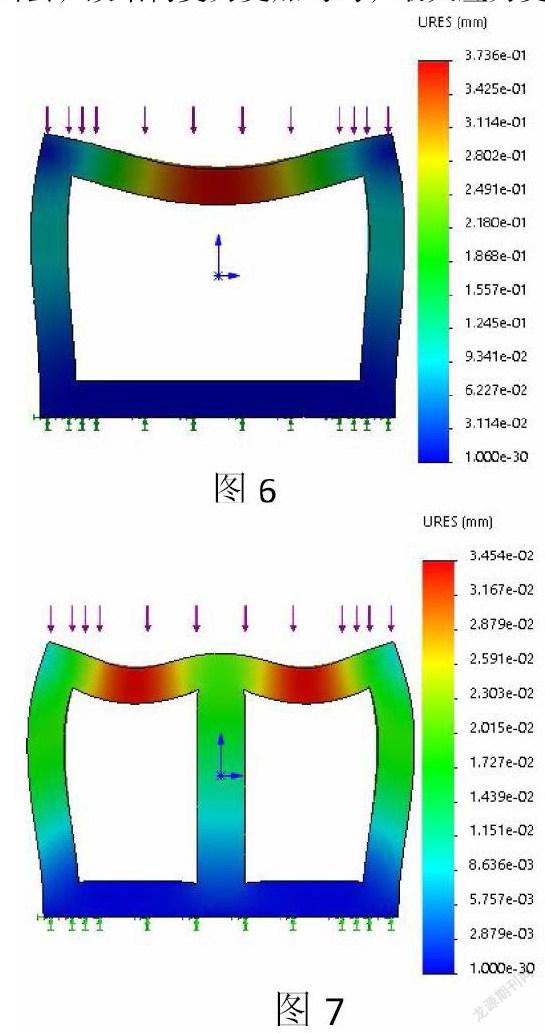
那么，我们可以从另一个角度去优化刚性且减小变形。可以将不加筋板的零件进行solidwork simulation分析，如图6，我们分析得出其在相同均布力下的最大变形量在上表面中间位置，为0.37mm。这个变形量比上述四种的变形量都要大，很显然，加强筋是有作用的，但是加强筋的位置不一样导致加强作用也不一样。

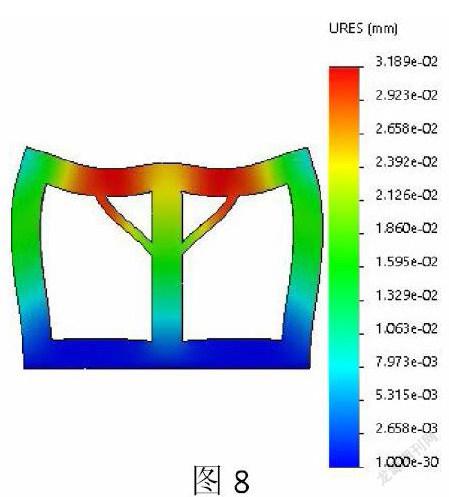
由于上表面中间变形最大，首先考虑在中间加一条立筋，这就解释了图3十字型的结构要优于其他结构的原因。如图7，在截面中间加一条立筋，为了保证加筋板后的零件质量和上述四种形式相同，则要保证截面面积一样，那么这条筋的厚度较上述四种类型要厚得多，分析出最大变形量在上表面的约四分之一位置，为0.035mm。但是这并不一定是最优的方案，因為此时的我们并不知道，若分出一部分面积，在图7中的最大变形量位置加上筋支撑，如图8所示，此时的最大变形量依然在上表面的约四分之一位置，为0.032mm，但是很明显，变形量较图7已经减少。

此时还可以继续增加图8中两侧斜筋的厚度，减小立筋的厚度，使得最大变形量最小，但是根据分析后会发现，此时的变化并不大;

4、结论

从中可以见得，优化结构截面的方式是通过分析原始状态下，不断的加强薄弱位置，削弱刚性大的位置，保持质量不变，我们会得出一种比较满意的截面，这样此时的结构截面就是较为优化的截面。通过这样的截面拉伸出来的三维模型即是我们所需要的结构。

以小见大，在现代计算机发达的年代，通过计算机solidwork simulation的辅助分析，我们可以不断的尝试新的结构，在最原始结构上使用软件分析出目标变形量，将此位置与变形较小位置用筋板相连，再次分析得出结果后进行 ，不断的迭代后，我们将会发现收敛的值，此时的结构就是我们所需要的目标结构。

参考文献：

[1]季霞. 机械结构优化设计的综述与展望之我见[J]. 建筑工程技术与设计， 2016， 000（012）：3028.

[2]陈永当， 鲍志强， 任慧娟，等. 基于SolidWorks Simulation的产品设计有限元分析[J]. 计算机技术与发展， 2012， 22（9）：4.