高中数学函数最值问题的教学思考

江苏省泰州市姜堰区罗塘高级中学 陈小进

数学是一门讲究思维的课程，活跃的思维有助于提高学生学习数学知识的效果。有效地传授给学生必要的数学解题思想与方法，可以帮助学生突破数学知识学习难点，尤其适用于函数最值问题等一些难点数学类型题的专项教学与指导。

一、巧借判别式，求解函数最值问题

针对一般的函数式，可以通过巧妙变形来转换成ax2+bx+c=0（a≠0）这种标准函数形式，然后依据Δ≥0这个判别式来对相应的最值问题进行求解。

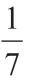
在求解出函数最值之后，要注意将其代入原式中进行验证。此外，在借助判别式法求解问题时，还要注意在保证分母以及分子中的二次项系数都不可为零的条件下进行整式转换，并且在转换之后还要考虑分子的二次项系数为0和不为0这两种情况，确保整体函数最值计算分析的全面性与结果的准确性。

二、巧借配方法，求解函数最值问题

例2：试求y=x2-4x+1在[1，4]上的最值。

解析：针对该道函数问题的求解，可以首先将给出的函数表达式进行配方转换，这样可以得到y=（x-2）2-3这一形式。通过观察这一表达式，可以快速得到在x=4的时候，y的最大值为1；在x=2时，y的最小值为-3。相较于利用函数判别式计算的方式，将函数表达式转化成这种配方形式，对区间最值问题的求解有很大帮助。

在借助配方法进行函数最值问题求解中，需要注意重点关注与考虑函数图像对称轴与给定函数区间之间的位置关系。函数取值范围和对称轴之间一般有如下两种关系：对称轴处于给定区间之内的时候，那么待求最值结果位于给定区间的2个端点位置以及对称轴上的顶点处；当对称轴位于给定区间之外的时候，最值位置处于给定区间的端点位置。

三、巧借不等式，求解函数最值问题

在求解函数最值问题中使用不等式法时，具体需要依据“一正二定三相等”的分析及判断依据。

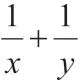
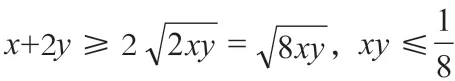
总之，函数最值问题是高中生需要掌握的一类数学类型题。在平时的解题教学中，针对该种类型的数学题，可以配合例题的展示传授一些基本的数学思想以及常用的求解方法，不断提升学生求解函数最值问题的能力。