基于遗传算法的城市轨道交通车站出入口布局规划方法
刘兆义 叶霞飞 王 治
(1.中铁第四勘察设计院集团有限公司,430063,武汉;2.同济大学道路与交通工程教育部重点实验室,201804,上海;3.上海市轨道交通结构耐久与系统安全重点实验室,201804,上海 ∥ 第一作者,助理工程师)
0 引言
城市轨道交通车站承担着为城市轨道交通系统集散客流的任务,车站出入口设置的合理性将影响城市轨道交通系统与城市外部空间之间的联系。目前,国内城市轨道交通车站出入口大多贴近车站主体建筑设置,出入口数量较少,乘客前往车站的步行接驳时间较长。
对于城市轨道交通车站出入口设计,国外学者的研究集中在车站地下空间资源利用形式和建筑设计方面。文献[1]从轨道交通网络的总体设计角度出发,分析了轨道交通在规划设计时应考虑的地下空间信息要素。文献[2]通过对印度尼西亚雅加达捷运隧道工程的案例研究,分析了城市轨道交通对城市地下空间的利用有效性原则。国内学者的研究集中在车站出入口的建筑结构设计、接驳交通设施衔接和地下空间资源利用等方面。文献[3]将出入口分为3类,采用Logit模型对乘客的出行偏好进行预测,通过计算得到备选出入口位置的选择人数,进而判别备选位置是否需要设置出入口;但并未给出设置出入口的人数判定标准,因此无法确定出入口的数量。文献[4]以降低社会总成本为目标,构建了基于一定约束条件的城市轨道交通车站出入口规划布局合理方案的搜索模型;该模型采用枚举法搜索所有的备选方案,效率较低。
就城市轨道交通车站出入口布局规划的方法而言,从国内外的研究现状来看,主要存在如下问题:一是缺少对车站出入口位置、数量和出入口通道的综合考虑,仅对车站出入口的数量或位置进行单独研究;二是模型的求解算法采用传统的枚举法,效率不高。
本文提出了基于遗传算法的城市轨道交通车站出入口布局规划方法。在探讨城市轨道交通车站出入口布局规划总体原则和研究范围的基础上,基于GIS(地理信息系统)平台建立了车站出入口布局研究范围内GIS数据库,提出了车站备选出入口选取原则和车站出入口布局备选方案生成方法。以社会总成本最小为优化目标,利用遗传算法原理实现了车站出入口布局最优方案的求解。
1 城市轨道交通车站出入口布局备选方案生成方法
1.1 车站出入口布局规划总体原则
城市轨道交通车站出入口是免费向社会提供服务的基础设施,主要效益来自于其接驳服务产生的社会效益。如何使车站出入口既能满足交通及社会经济活动的需求,同时又避免出现因出入口设置过多造成社会资源浪费的现象,是本文需要解决的问题。
相较于紧邻车站主体设置出入口,向车站周边延伸一定范围建设出入口设施,能够降低出行时间成本和交通安全成本。如果在一定时期内,因出入口设施修建而节省下来的出行时间成本及交通安全成本能平衡甚至超出因设施建设、运营、维修而新增的社会成本,从社会成本总和的角度考虑,就达到了以设施建设换取社会总成本下降的目的。
1.2 车站出入口布局规划研究范围的确定方法
确定车站出入口布局规划研究范围是为出入口布局规划和社会总成本计算划定一个边界。因受到车站密度、线路站间距等条件的限制,车站出入口离开车站主体建筑存在距离上限。本文通过调查分析上海、东京和香港城市轨道交通车站出入口通道长度的规律来确定距离上限。
1.2.1 上海、东京、香港城市轨道交通车站出入口通道长度调查与分析
选取上海市319座城市轨道交通车站、东京市232座地铁车站和香港93座地铁车站,对其出入口通道长度进行统计。这些车站均含有多个出入口通道。统计时记录该车站最长出入口通道的长度。上海、东京、香港轨道交通车站最长出入口通道长度的统计结果如图1所示。
由图1可知,上海城市轨道交通车站最长出入口通道长度在0~100 m范围内的车站数占比88.7%,在0~200 m范围内的车站数占比99.4%;东京地铁车站最长出入口通道长度在0~100 m范围内的车站数占比84.9%,在0~200 m范围内的车站数占比97.0%;香港地铁车站最长出入口通道长度在0~100 m范围内的车站数占比74.2%,在0~200 m范围内的车站数占比89.2%。由此可见,上海、东京、香港城市轨道交通车站最长出入口通道长度总体规律基本一致,绝大多数车站的最长出入口通道长度在0~200 m范围内。

图1 上海、东京、香港的城市轨道交通车站最长出入口通道的长度累计占比曲线
1.2.2 车站出入口布局规划研究范围的确定
参照上海、东京和香港城市轨道交通车站的出入口通道长度调查分析结果,将出入口离开车站主体建筑的距离L的上限取为200 m。对于城市轨道交通车站,由L来确定车站出入口布局规划的研究范围(见图2)。
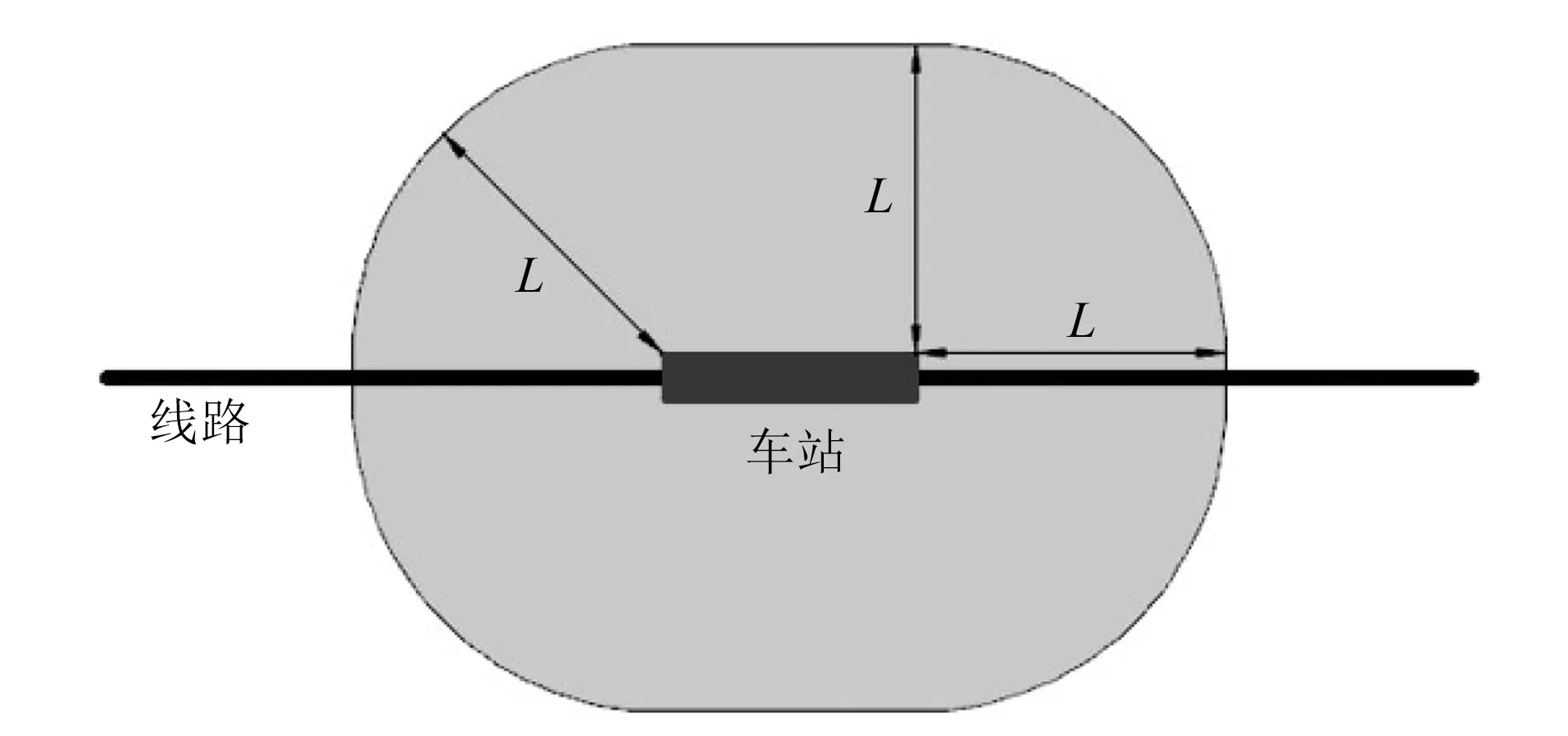
图2 车站出入口布局规划研究范围示意图
1.3 车站出入口布局研究范围内GIS数据库的构建方法
根据车站周围相关资料,建立车站出入口布局研究范围内GIS数据库,包含城市轨道交通车站、城市道路系统、建筑、车站周边道路交通站场设施。
城市轨道交通车站在其研究范围内是交通出行的起点或终点,根据需求建立车站模型,车站的形心点用点要素表示。对于城市道路系统,将城市道路全部抽象成线要素,机动车道和步行系统分开。机动车道路抽象为道路中心线,步行道路(包含人行道、交叉口处人行横道)依附于机动车道路,分布于两侧。对车站出入口布局研究范围内的建筑,通过建筑的出入口与步行道路形成连接。
在出入口布局研究范围内,车站的进出站客流除了会通过步行到达车站周围的居住区、商业区、办公区等区域,也会通过公交车站点、自行车停放场、汽车停车场、出租车站等车站周边道路交通站场设施,到达研究范围以外的目的地。在GIS数据库中,交通站场设施用点要素表示,位于步行道路上(见图3)。

图3 车站出入口布局研究范围内GIS数据库的构建
1.4 车站备选出入口的确定方法
作为进出站设施的出入口,需要布置在出入口布局研究范围这个较小的步行交通环境内行人聚集的位置上。本文将出入口布局研究范围内产生进出站客流的源头点作为车站的备选出入口。在GIS数据库中,位于步行道路系统中的重要建筑出入口道路和交通站场设施点,即为车站的备选出入口。
1.5 车站出入口布局备选方案的生成方法
车站备选出入口通过出入口通道与车站连接,本文假定出入口通道均沿既有城市道路中心线修建。道路中心线构成了单线路网,道路两侧的步行道路构成了双线路网。本文1.4节中的车站备选出入口均位于双线路网上,双线路网上的备选出入口和车站在单线路网上均有唯一确定的位置与其对应,如图4所示。

图4 车站备选出入口在单线和双线路网上的位置示意图
在单线路网上,采用Dijkstra算法,寻找备选出入口与车站之间的最短距离路径,且出入口通道沿最短路径修建(见图5)。
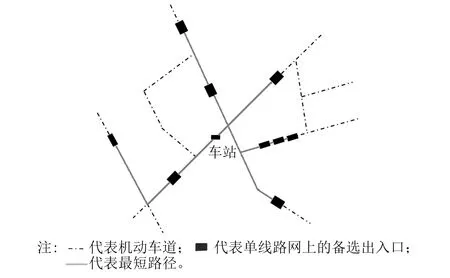
图5 各备选出入口与车站的最短路径示意图
当备选出入口的状态为设置车站出入口时,需要修建出入口通道将该出入口与车站连接。如果单线路网中某路段上有多条出入口通道经过,该路段上只修建一条通道,则所修通道上的客流量等于路段上几条出入口通道的客流量之和。
在车站出入口布局规划研究范围内,设置车站的备选出入口和其对应的通道,它们共同构成了车站出入口布局备选方案。通过改变各个备选出入口的状态,形成不同的出入口布局备选方案。
每个备选出入口Si(见图6)处是否设置车站出入口,将会影响Si处乘客前往车站的走行路径。例如,对某一备选出入口S1处的乘客而言,如果S1处设置车站出入口,则乘客通过S1对应的出入口通道K1到达车站;如果S1处不设置车站出入口,则S1处的乘客会沿着步行道路,在备选出入口集合中找到距离S1走行时间最短的备选出入口S3,然后进入S3对应的通道K3前往车站。
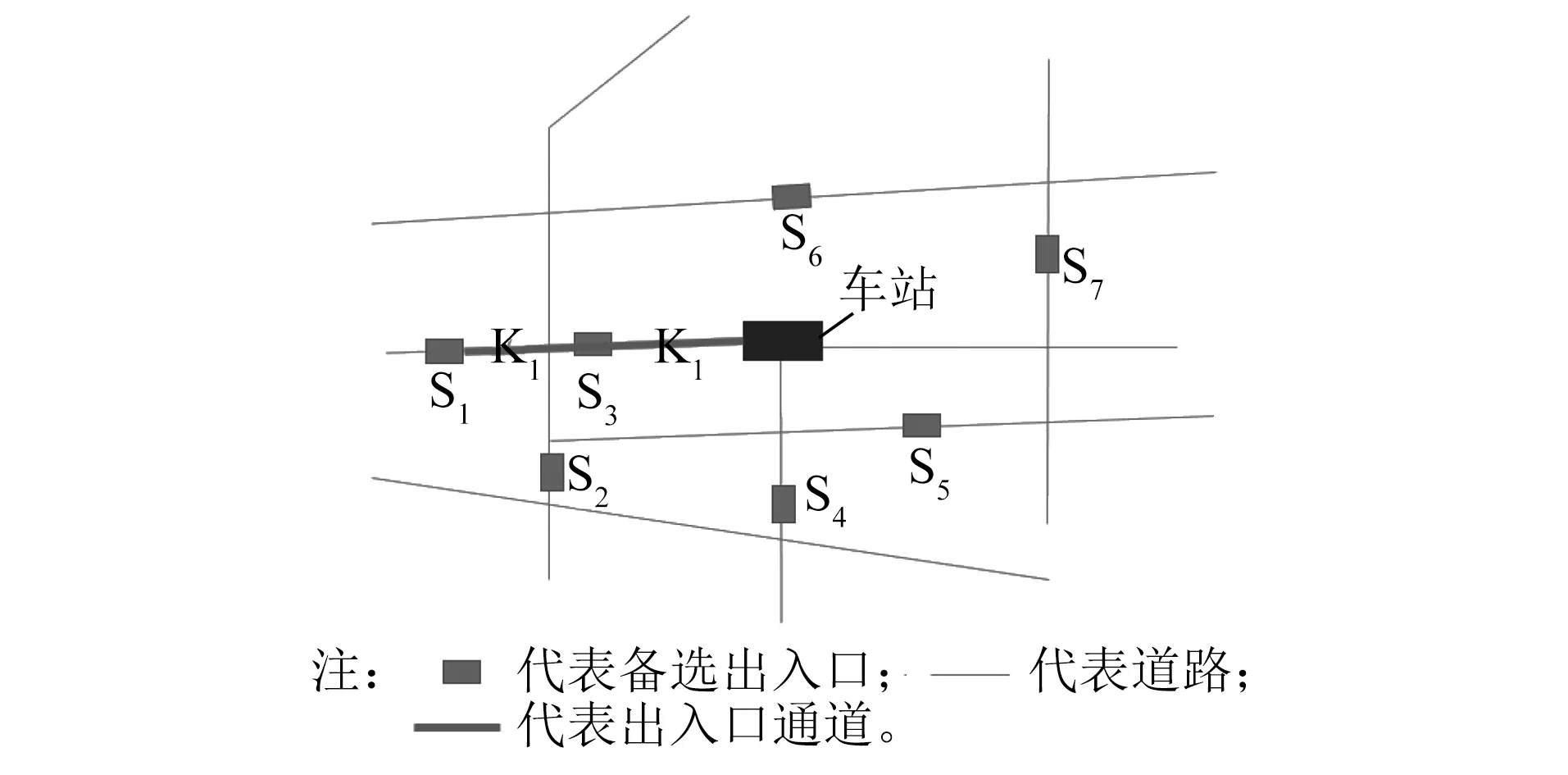
图6 设置车站出入口时乘客走行路径示意图
在不同的车站出入口布局备选方案中,研究范围内的乘客前往车站会采用不同的走行路径,具体走行路径根据该备选方案中各备选出入口的状态确定。
2 城市轨道交通车站出入口布局优化方法
2.1 模型假设
1) 乘客对出入口的选择。乘客对车站周围的交通环境比较熟悉,对走行时间有明确感知,会选择距离自己走行时间最短的出入口前往车站。
2) 乘客的走行速度和时间延误。乘客在地面人行道步行时,会受到人行道上无序穿梭步行者的干扰和恶劣天气(雨雪等)的侵扰,导致乘客在地面人行道上的走行速度慢于在出入口通道内的走行速度。乘客在地面走行时也会受到地面道路交叉口控制信号的干扰,存在一定的时间延误。
3) 出入口通道的走向。出入口通道均沿既有城市道路中心线修建。
4) 特殊出入口。在车站站房本体设置的出入口不在本模型考虑范围内。
2.2 社会总成本及目标函数
本文选取社会总成本最小作为方案的优化目标。社会总成本包括建设、运营、维修、出行时间、交通安全等成本及其他成本。
2.2.1 建设成本
Cjs=Ctf+Cwh+Czt+Cdl+Czx
(1)
式中:
Cjs——建设成本;
Ctf——地下通道或出入口的土方成本;
Cwh——地下通道或出入口的围护成本;
Czt——地下通道或出入口的主体结构成本;
Cdl——地下通道或出入口的道路成本;
Czx——地下通道或出入口的装修成本。
2.2.2 运营成本
Cyy,t=Cbj,t+Cnh,t
(2)
式中:
Cyy,t——计算期内第t年的运营成本;
Cbj,t——计算期内第t年的保洁成本;
Cnh,t——计算期内第t年的能耗成本。
2.2.3 维修成本
由于设施设备故障的不可预测性,采用经验取年费率的方法来计算维修费用。
Cwx,t=PtjssC1+PsbC2
(3)
式中:
Cwx,t——计算期内第t年维修成本;
Ptjss——土建设施建设费用;
C1——土建设施的年维修费率;
Psb——运营设备总费用;
C2——运营设备的年维修费率。
2.2.4 出行时间成本
CTR,t=CT,t+ΔCTP,t+ΔCTW,t
(4)
式中:
CTR,t——计算期内第t年因城市轨道交通车站出入口布局方案引起的出行时间成本;
CT,t——计算期内第t年步行进出站乘客接驳时间成本;
ΔCTP,t——计算期内第t年因出入口设施修建引起的非进出站行人过街总时间成本变化量;
ΔCTW,t——计算期内第t年交叉口机动车辆使用者延误时间成本的变化量。
2.2.5 交通安全成本
CSA,t=∑iNi,tCi,t
(5)
式中:
CSA,t——计算期内第t年城市轨道交通车站出入口布局方案对应的交通安全成本;
Ni,t——计算期内第t年过街行人第i类交通事故预测发生量;
Ci,t——计算期内第t年单起第i类交通事故的国民经济损失。
2.2.6 其他成本
Cqt,t=Cclnh,t+Cclpf,t+Csspf,t
(6)
式中:
Cqt,t——计算期内第t年的其他成本;
Cclnh,t——计算期内第t年因延误时间变化造成的机动车辆能耗成本变化量;
Cclpf,t——计算期内第t年因延误时间变化造成的机动车辆排放成本变化量;
Csspf,t——计算期内第t年由设施运营产生的排放成本。
2.2.7 目标函数
综上所述,目标函数为以上6部分成本之和的最小值,即:
minCsh=Cjs+Cyy,t+Cwx,t+CTR,t+CSA,t+Cqt,t
(7)
式中:
Csh——计算期内的社会总成本。
2.3 最优方案的求解
每个车站备选出入口的开口状态发生改变,便会形成一种新的出入口布局备选方案。备选方案数量众多,车站出入口布局优化的关键在于从大量的出入口布局备选方案中选出社会总成本最小的布局方案。为了有效地解决上述问题,引入遗传算法。
遗传算法从初始种群出发,评判种群中个体的适应度,采用优胜劣汰的自然法则选择部分个体,再通过对当前种群施加交叉、变异等遗传操作来产生新一代的种群。逐代进化使种群进化到包含近似最优解的状态,最终获得最优解。遗传算法对自变量及优化目标函数无特殊要求,适用于类似于出入口分布等离散型问题的求解。
基于上述理论,本文采用遗传算法通过以下7个步骤求解车站出入口布局优化问题:
1) 编码:在进行遗传算法搜索之前,首先将求解数据表示成一串由二进制编码或十进制编码组成的字符串。该字符串称之为“个体”,多个字符串组成“群体”。在出入口布局优化的过程中,此步骤即为生成长度为潜在备选出入口总个数的0、1字符串,如(1,1,1,1,0,0,1,0,1)。
2) 初始群体的生成:随机生成NP个个体作为初始群体P(0)。在出入口布局优化的过程中,此步骤即为随机生成NP个出入口布局备选方案,作为布局优化的初始备选方案集,如{(1,1,1,1,0,0,1,0,1),(0,0,1,1,0,0,1,1,1),(1,1,0,1,0,1,1,0,1),…}。
3) 个体适应度评价:计算群体P(t)中各个个体的适应度,该适应度与优化目标函数值相关联。优化目标函数值越小,个体适应度越大,即每个出入口布局备选方案的社会总成本越小,该方案的适应度越大。
4) 选择运算:根据群体中个体的适应度,按照一定的规则或方法,选择一些优良个体遗传到下一代群体,其中个体适应度越大,越容易被选择,反之亦然。对每一个出入口布局备选方案而言,社会总成本越小,越容易被选择进入下一代备选方案集,社会总成本越大的方案越容易被淘汰。
5) 交叉运算:在群体中,对选中的成对个体,以某一概率交换它们的部分值,产生新的个体。例如,两个出入口布局方案(1,1,1,1,0,0,1,0,1)和(0,0,1,1,0,0,1,1,1),交换前两位,即可产生两个新的布局方案(0,0,1,1,0,0,1,0,1)和(1,1,1,1,0,0,1,1,1)。
6) 变异运算:对群体中所选中的个体,以某一概率改变某一个或某一些值。例如,某出入口布局方案(1,1,1,1,0,0,1,0,1),变异最后一位,产生新的布局方案为(1,1,1,1,0,0,1,0,0)。
7) 终止条件判断:群体P(t)经过选择、交叉和变异运算之后得到下一代群体P(t+1),并继续进行一系列的运算,不断循环迭代,直到新生成的方案的适应度不再改变,即搜索到了最小社会总成本对应的出入口布局方案,终止计算并输出该最优解。
为防止每一代种群中成本值最小的方案被变异运算或交换运算所改变,采用精英保留策略,将每一代种群中的精英个体(成本值最小的方案)直接遗传给下一代种群。每一代种群中的精英个体数量可能是1个或多个。
3 车站出入口布局的最优方案分析
3.1 计算参数与假设
以上海市某城市轨道交通地下中间站为研究对象,对车站出入口布局的最优方案进行分析。该车站出入口及通道于2009年开始建设,建设期1年,运营期30年。
依据车站备选出入口选取原则,在车站出入口布局规划研究范围内,共有56个备选出入口,如图7所示。

图7 车站周边备选出入口示意图
运营期间,每天高峰时段为4 h,平峰时段为12 h,客流年增长率为1.7%。年物价上涨率取6%,社会折现率取8%;设施的折旧年限为100年,残值率取4%;行人在人行道、人行横道的步行速度取1.2 m/s,在通道内的步行速度取1.5 m/s[6];行人通过人行横道的延误时间取43.7 s[7]。人行地道宽度的设计能力取1 380人/(mh),通道设计宽度计算值不足3.75 m的按3.75 m修建[4]。土建设施年维修费率取0.01,其他设备维修费率取0.02;运营耗电取60 W/(m2h),运营初年能耗成本取76元/m2。
3.2 出入口布局最优方案的求解
采用车站出入口布局规划方法进行方案的生成、评价及优化,初始种群的个体数取30,变异率取0.5,交换率取0.6,进行300次遗传。观察遗传算法找寻最优方案的过程,目标函数值在进行多次遗传运算后,最终稳定于55 824.88万元(见图8),此时找到出入口布局最优方案,终止运算。
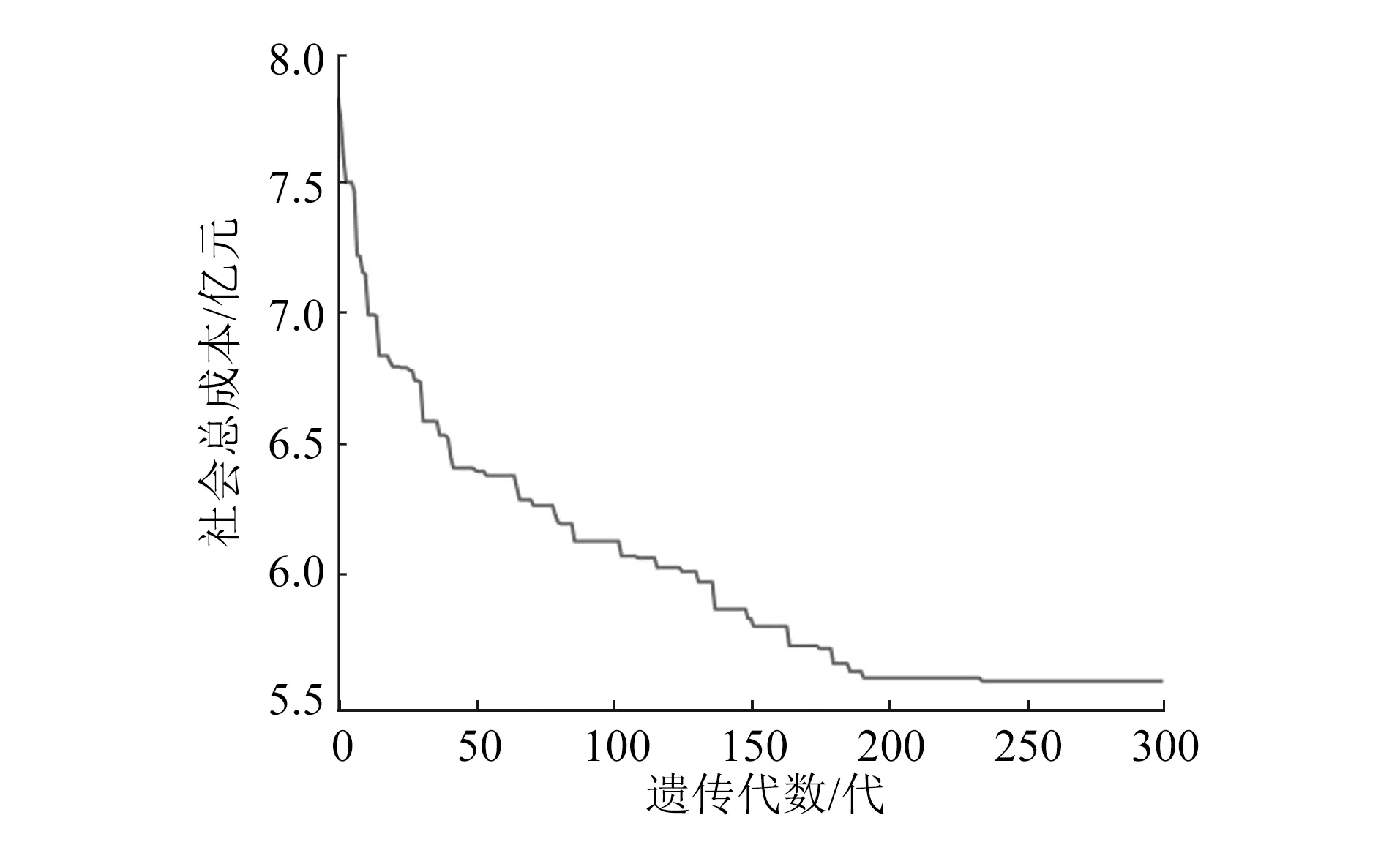
图8 每一代种群中精英个体的社会总成本
出入口布局的最优方案为:在2号、8号、9号、10号、23号、32号、33号、35号、40号、43号、50号、53号、55号备选出入口位置设置车站出入口,共设置13个车站出入口,如图9所示。

图9 车站出入口布局最优方案示意图
4 结论
1) 提出了城市轨道交通车站出入口布局备选方案的生成方法。在探讨城市轨道交通车站出入口布局规划总体原则和研究范围的基础上,基于GIS平台建立了车站出入口布局研究范围内GIS数据库,提出了城市轨道交通车站备选出入口的选取原则和车站出入口布局备选方案的生成方法。
2) 提出了城市轨道交通车站出入口布局最优方案的求解方法。在对城市轨道交通车站出入口布局方案评价指标进行量化的基础上,以社会总成本最小为优化目标,利用遗传算法原理实现了车站出入口布局最优方案的求解。

