一种应用于轮轨滚动接触的非赫兹型简化计算模型

李粮余 田春香, 周佳仪 安博洋 王 平

(1.中铁二院工程集团有限责任公司,成都 610031；2.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031)

1 研究背景

高速铁路轮轨关系是制约列车运行速度以及影响车辆安全运营的关键问题[1-2]，因此，需要有效的轮轨接触模型以分析轮轨间的相互作用，能够准确、快速地求解非赫兹滚动接触行为。由于基于边界元法[3]和有限元法[4]的准确接触模型的计算时间较长，轮轨磨耗预测需要进行数百万次计算以模拟实际的运行距离，因此，无法高效预测轮轨磨耗。

在提高计算效率的同时考虑轮轨非赫兹滚动接触行为，一些学者提出了几种简化的非赫兹接触模型。Kik和Piotrowski[5]提出了“虚拟渗透”的概念，假设压应力沿横向的变化与接触斑纵向边界的分布保持一致，该模型可快速地确定接触斑形状。基于虚拟渗透方，Linder提出了另一种接触斑形状的确定方法，即将接触斑视为一系列沿着纵向分布的条带。然而，Kik和Linder等人的方法均无法获得较为准确的压应力分布。相比较而言，Ayasse和Chollet[6]开发的STRIPES接触模型，采用赫兹接触理论求解每一条带上的压应力分布，可获得较为准确的结果。类似地，Sichani[7]等提出了一种名为ANALYN的接触模型，考虑了弹性变形对接触斑和应力的影响。

上述简化接触模型的切向计算一般采用Kalker简化理论及其FASTSIM算法，由于FASTSIM是基于椭圆接触假设而开发的，因此，处理非赫兹接触问题时需对椭圆计算所得到的柔度系数进行修正。在Kik和Piotrowski的模型中，通过接触斑面积和长短半轴比两个参数定义一个等效椭圆，进而计算该椭圆的柔度系数，并作为非赫兹接触斑的切向计算参数；Linder和STRIPES接触模型则将接触斑内每个条带等效为一个局部椭圆，并计算相应的柔度系数。尽管按照上述方法可得到较为准确的蠕滑力，但由于FASTSIM假设接触应力与弹性位移呈线性关系并且引入了不真实的抛物线型切向应力边界条件，这些方法仍无法获得较为准确的切向接触结果。为此，Sichani提出了一种基于Kalker的条带理论和简化理论的新型接触计算方法——FaStrip，可获得更为准确的切向接触结果。

由于STRIPES接触模型可较好地兼顾计算精度与效率，已广泛应用于车辆轨道/道岔动力学、接触力学建模以及磨耗预测。但在最近的研究中发现 STRIPES接触模型在某些极端非赫兹工况下存在较大计算误差[8]。因此，本文对STRIPES接触模型进行改进，提高其计算精度和稳定性。

2 STRIPES算法

2.1 法向接触计算

轮轨法向接触问题中，法向间隙f(y)、渗透量δ以及弹性变形u(y)之间存在以下关系：

(1)

式中：R——接触点处车轮半径(m);

x——滚动方向的坐标；

y——横向方向的坐标。

应力p(x,y)是在物体表面产生的弹性变形，可用Boussinesq-Cerruti方程表示：

(2)

式中：Aij——影响系数，代表单元j处的单位载荷引起单元i处的变形；

V——材料的泊松比；

E——材料的弹性模量(MPa)。

为简化求解式(1)的计算过程，STRIPES基于虚拟渗透原理，采用比例系数ε替代计算弹性变形。在该算法中，将接触斑沿滚动方向划分为条带，如图1所示。接触斑的横向边界可简化为：

h(y)=εδ-f(y)≥0

(3)

式中，ε由赫兹理论计算得到：

(4)

式中：A0——第一个接触点处的纵向曲率；

B0——第一个接触点处的横向曲率；

n0、r0——无量纲赫兹常数。

假设每个条带对应一个局部等效椭圆，且具有相同的赫兹特性，每个条带的半轴长度a(y)可利用式(5)求解：

(5)

式中：m——无量纲赫兹常数。

接触斑内任意单元的应力为：

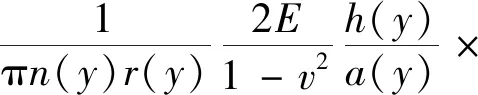
(6)

2.2 切向接触计算

在STRIPES中切向接触问题采用Kalker的FASTSIM算法进行处理，假设每个条带具有各自的椭圆特性，在每个条带中使用基于椭圆接触开发的FASTSIM算法进行计算，如图1所示。在剪切应力设定为0的接触斑前沿计算每个条带的剪切应力增量：

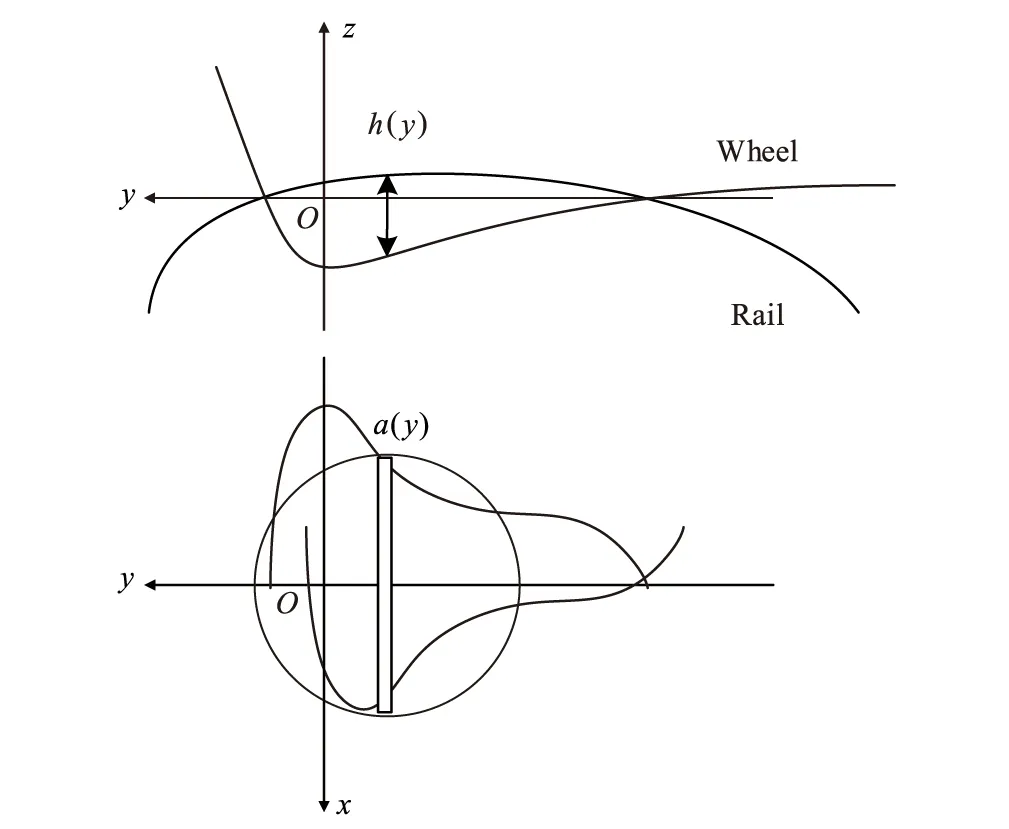
图1 STRIPES模型示意图

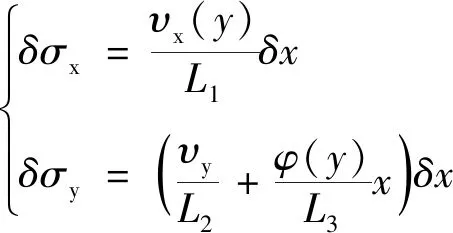
(7)

(8)

式中：υx(y)——每个条带处纵向蠕滑率；

φ(y)——每个条带处的自旋；

υy——横向蠕滑率；

L1、L2、L3——每个局部椭圆的柔度系数。

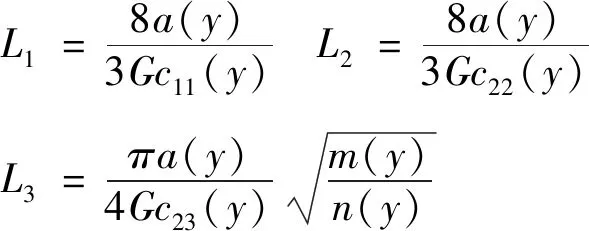
(9)

式中：c11,c22,c23——Kalker蠕滑力系数；

G——剪切模量(MPa)。

假设牵引边界遵循抛物线分布：

(10)

式中：μ——摩擦力系数。

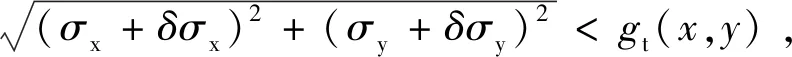
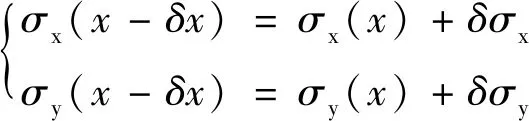
(11)

否则，该点位于滑动区，此时剪切应力为：

(12)

在实际情况中牵引力界限并非抛物线型，但这一假设对于确保在FASTSIM中得到相对准确的蠕滑力曲线是必不可少的，因此，在实际切向计算中，牵引力边界由式(6)中椭圆分布变为式(10)中的抛物线分布。有关此模型的更多详细信息，请参阅文献[7]。

3 STRIPES模型修正

3.1 由接触边界确定可变比例系数

从式(4)可以看出，STRIPES中假定比例系数ε为常量，忽略了接触区域上曲率的变化，接触斑形状的确定仅取决于第一接触点。因此，本文通过采用每个条带处变化的比例系数ε(y)替换单一系数ε从而对STRIPES算法进行修正：

(13)

将式(13)代入式(3)、式(5)和式(6)，可获得新的接触斑区域以及应力分布。与KP和Linder等其他虚拟渗透方法相比，STRIPES接触模型的优点是当接触斑为椭圆形的情况下可得到与赫兹理论一致的结果，而其他两种方法则不能。由于椭圆接触时曲率保持恒定，考虑可变比例系数并不会改变STRIPES接触算法的特性，此时ε(y)保持恒定且等于ε，因此ε属于ε(y)的一种特殊情况。

3.2 一种获得合理渗透量的简单迭代方法

与其他接触模型一样，STRIPES模型式(3)中的渗透量δ也是未知的，为使模型计算所得法向力与给定法向力一致，需迭代求解。之前的研究中常使用赫兹理论所得渗透量作为δ，原因在于LMa-CN60组合轮轨廓形产生的接触斑接近于椭圆形。然而在非椭圆形的接触情况下赫兹渗透量和实际渗透量之间可能存在较大差异，因此有必要增加迭代过程以获得真实渗透量。据此，本节提出了一种实现该过程的新方法。

以给定的法向力N为已知参数，由式(14)计算所得赫兹渗透量δH作为初始渗透量。

(14)

按式(15)进行迭代，直至由式(6)应力积分计算得到的输出法向力P与给定的法向力N相等。

δn=λδn-1

(15)

式中：λ——无量纲比例因子。

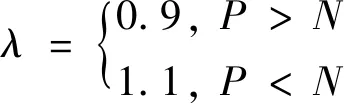
(16)

由于法向力对渗透量值的变化非常敏感，较大的比例因子可能使输出法向力产生剧烈波动，而小值导致不能快速收敛。式(16)中所定数值是由大量工况计算确定以确保能够加速迭代过程。尽管需要进行渗透量迭代，简化模型的计算速度仍比精确模型快得多。

3.3 与FaStrip相结合的非椭圆方法

如2.2节所述，STRIPES借助Kalker的FASTSIM算法进行切向计算，然而该算法由于假设剪切应力在黏着区呈线性分布且遵循抛物线牵引力边界而不能得到令人满意的滚动接触解。为提高计算精度，本节引入名为FaStrip的新切向接触模型来代替FASTSIM。

FaStrip算法将Kalker条带理论、线性理论与FASTSIM算法结合起来，可以考虑任意组合的纵向、横向以及自旋蠕滑率。该方法假设接触区为椭圆形并且沿滚动方向将其离散成条带，通过改进的条带理论计算黏着区的剪切应力分布。为保持与线性理论相同的蠕滑曲线斜率，该理论引入了3个校正因子，且滑动区的剪切应力分布遵循椭圆牵引界限。因此，FaStrip算法可在任意接触椭圆形状的情况下提供足够准确的剪切应力和滑动量值，并保持与FASTSIM相同的计算效率。有关FaStrip的更多详细信息，请参阅文献[7]。

此外，为了适应非椭圆接触条件，基于椭圆假设开发的FaStrip算法应对由椭圆条件计算的条带柔度系数进行修正。这种改进可以确保滑移区域中剪切应力方向的正确性，否则将影响蠕滑力的横纵向分量。

FaStrip算法中仍然使用式(9)中每个条带的3个柔度系数，将式(7)修正为：

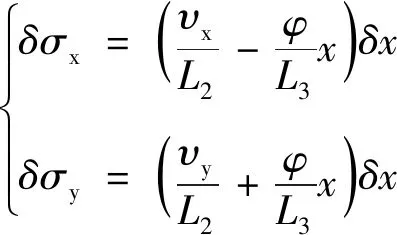
(17)

此改进充分考虑了自旋对纵向剪切应力的影响，当车轮与轨顶相接触时，接触角的变化较小，轮轨接触遵循半空间假设，接触斑可被视为平面，接触斑内自旋和蠕滑也都保持不变。

另一方面，滑动区饱和剪切应力受限于式(18)中的椭圆牵引边界：

(18)

4 计算结果分析

修正STRIPES的接触模型(Modified STRIPES)实现了上述改进，该算法基于MATLAB软件开发，计算速度约比FORTRAN程序编码的Kalker 的CONTACT程序快200～300倍。

本节旨在评估修正STRIPES接触模型计算法向和切向接触的能力。采用轨底坡1∶40的轮轨标准型面组合S1002CN-CN60，轮轨界面之间的摩擦系数为0.3。-3～7 mm 10种不同横向位移下接触形状和压力的变化情况，如图2所示。本文取轮对放置在中心位置(Δy= 0 mm)且横向位移分别为2 mm和 6 mm时的工况作为典型接触工况进行详细分析。

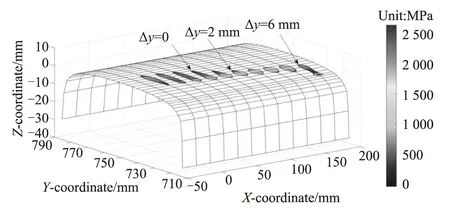
图2 CONTACT预测的横移量范围为-3～6 mm(从左到右)时接触形状、压力变化图

4.1 法向接触

以Kalker的CONTACT程序作为对照，修正STRIPES接触模型与原始STRIPES模型计算的沿横向(在x=0处)接触斑和法向应力分布情况进行了比较，如图3～图5所示。从图3～图5中可以看出，Δy=0 mm时，接触斑处于高度非赫兹情况，右边界大于左边长度。与STRIPES相比，修正STRIPES模型计算的接触斑和最大应力结果均得到一定的改善，接触斑宽度和最大应力的误差分别从22.06%降至8.94%、12.57%降至4.13%。Δy=2 mm时，三种接触模型中的接触斑和应力分布都比较接近，相较之下修正STRIPES模型计算结果更为准确，与CONTACT结果基本一致。Δy=6 mm,时接触斑由两个椭圆合并组成，STRIPES无法正确估计右侧的真实接触形状，而修正后的STRIPES模型明显改善了接触斑形状和最大应力的结果，更接近参考值。

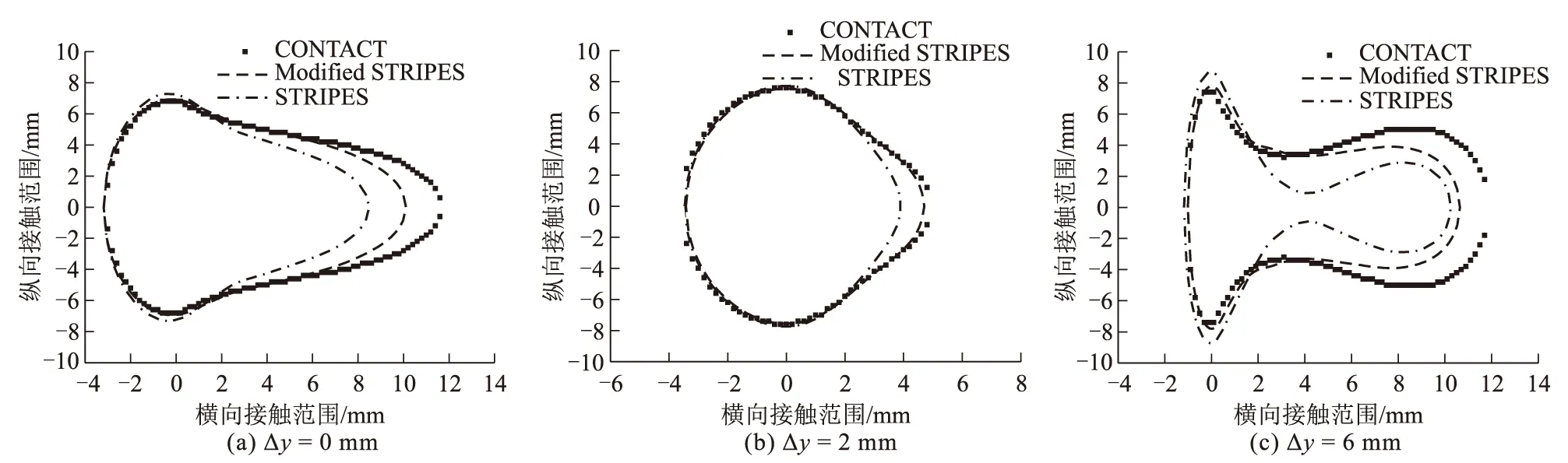
图3 三种工况接触斑图(x=0)

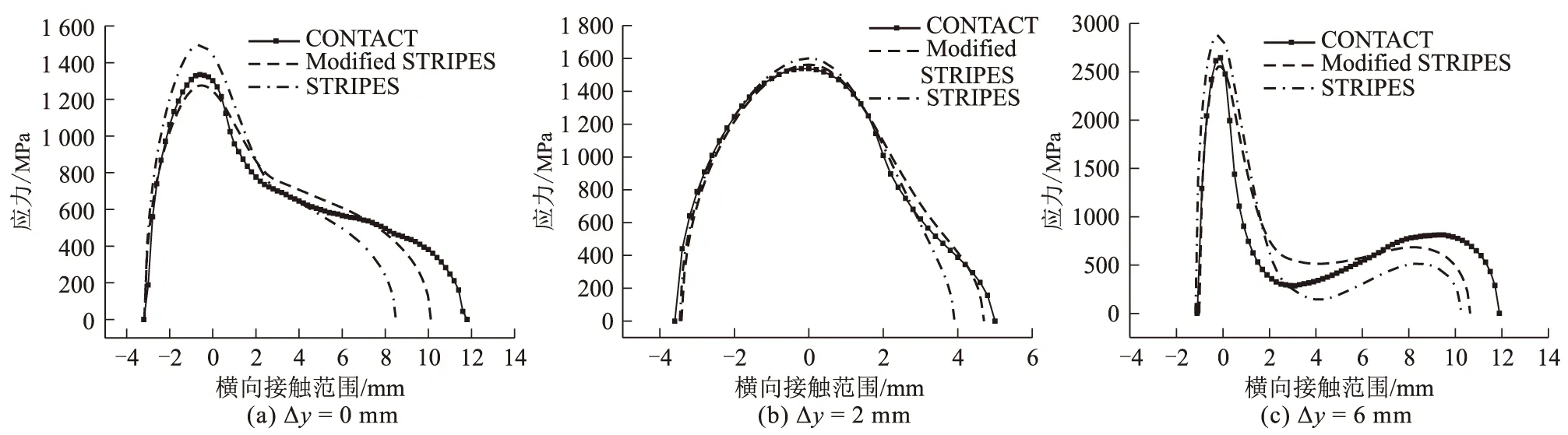
图4 三种工况应力分布图(x=0)

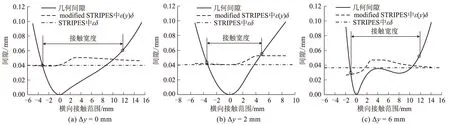
图5 三种工况几何接触间隙图(x=0)

上述改进归因于修正STRIPES模型中使用的变化比例系数的影响。通过对不同横移量时几何间隙以及修正STRIPES模型与原始STRIPES模型中分别使用的渗透量值ε(y)δ、εδ对比发现，由第一接触点估计的εδ能够很好地计算左侧边界，原因在于几何间隙的左边部分接近椭圆接触间隙。因此，三种接触模型在接触斑形状和应力的负方向上能够相互对应。而此时几何间隙的右侧显示非椭圆特征，STRIPES模型会低估接触区域的正横向边界。相比之下，使用变化比例系数可明显改善法向接触解。值得一提的是，在Δy= 6 mm工况下，两种简化模型比例系数与渗透量的乘积并不相同，渗透量会因第3.3节中所述的迭代过程而发生变化。

4.2 切向接触结果

三种典型工况下的切向接触结果如图6所示，箭头指向剪切应力的方向，长度与剪切应力的大小成正比。从计算结果中可发现，两种简化模型都可获得令人比较满意的黏滑分布和剪切应力值，其中修正STRIPES模型结果与CONTACT更为接近。

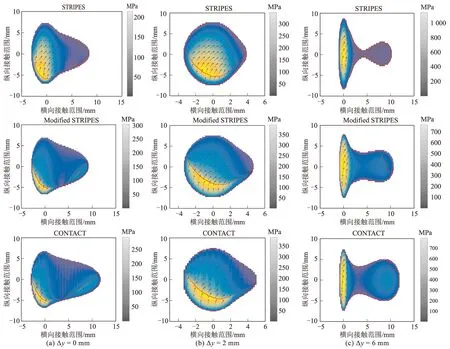
图6 不同横移量下切向力分布对比图

但两种简化接触模型预测的剪切应力分布在某些工况下仍存在一定差异。前两种工况下，接触区域中黏着区域居多，STRIPES模型预测的剪切应力明显小于其他两种算法，而最后一种工况则相反。这种现象主要是由于采用不同的牵引力边界条件以及STRIPES模型在黏着区域中假设剪切应力呈线性分布所导致。三种典型工况的总剪切应力及其分量沿纵向的分布情况(在y=0处)，如图7～图9所示。由图7～图9可知，本文提出的改进模型可以获得更接近于CONTACT的非线性剪切应力分布结果，从而进一步验证了本文所提出的改进模型在提高接触计算精度方面的有效性。

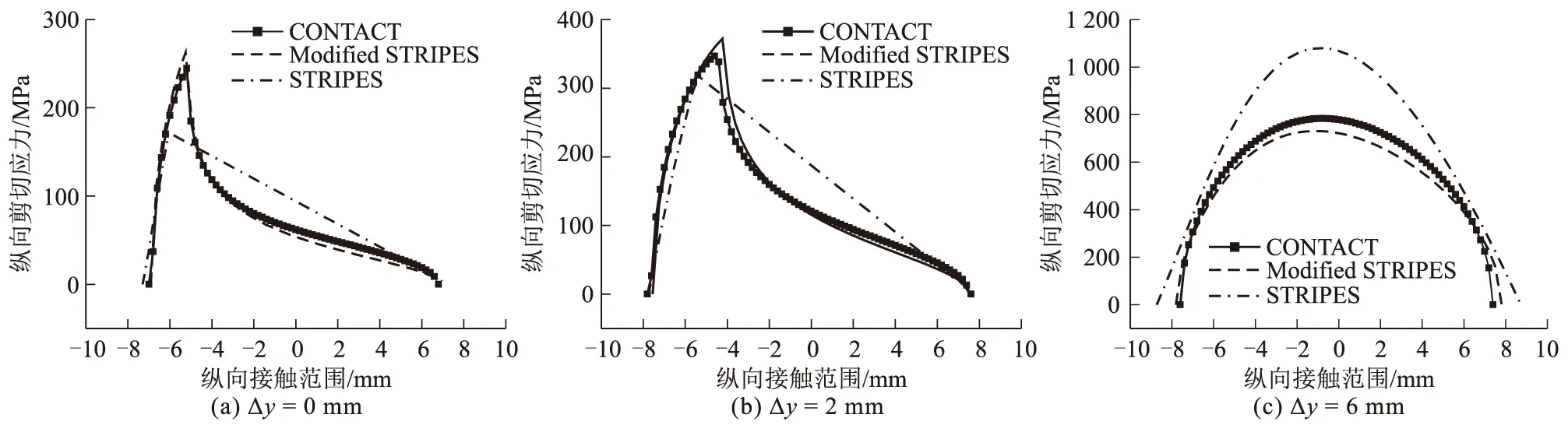
图7 纵向剪切应力对比图(y=0)

图8 横向剪切应力对比图(y=0)

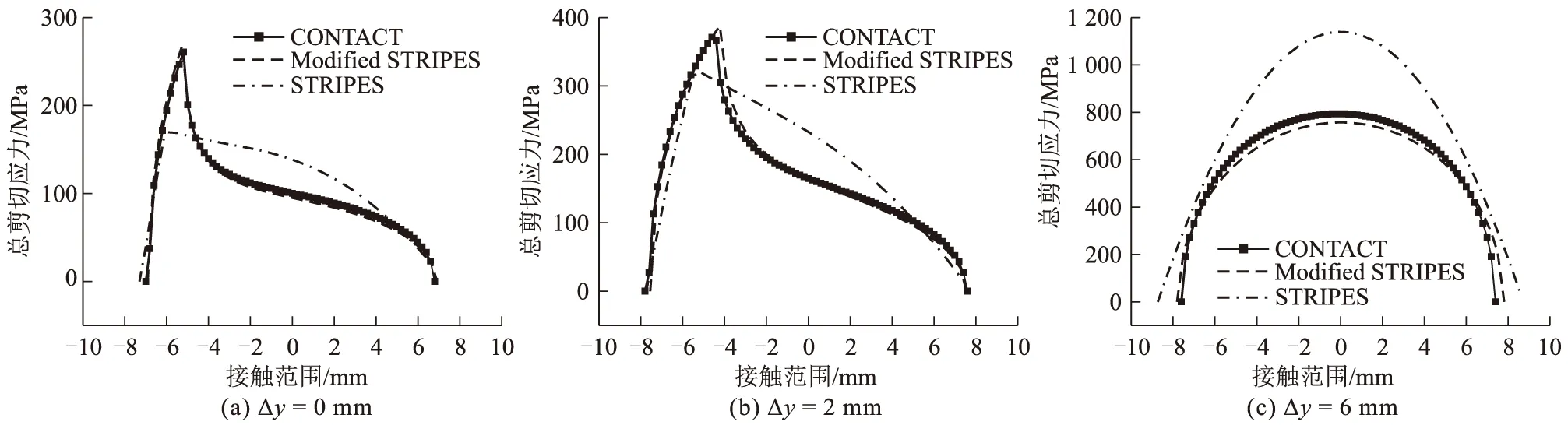
图9 总剪切应力对比图(y=0)

4.3 接触力预测

本节旨在评估简化方法预测接触力的有效性。接触力作为车辆动力学仿真的重要输入量，其准确地进行预测对于车辆动力学仿真计算，尤其是车辆过曲线或道岔等特殊工况时有重要影响。

三种工况下渗透量与接触力的关系曲线如图10所示。在前两种工况下，两种简化的接触模型结果与CONTACT能够较好地吻合。在最后一种工况下，尽管修正STRIPES模型显著改善了STRIPES的计算精度，但仍存在进一步的改善空间。

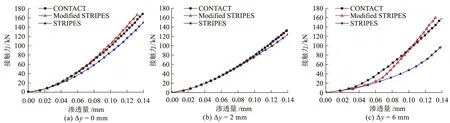
图10 不同横移量下渗透量与接触力关系的对比图

纯纵向蠕滑率变化时产生的纵向蠕滑力曲线，如图11所示。修正STRIPES模型在前两种工况可以获得更接近CONTACT的计算结果，相比之下，原始STRIPES中蠕滑力的增加速度更缓慢。由于最后一种工况 Δy=6 mm中两种接触模型所得接触斑形状与CONTACT相比存在一定差异，两种模型所得蠕滑力曲线的偏差较另外两种工况偏大。

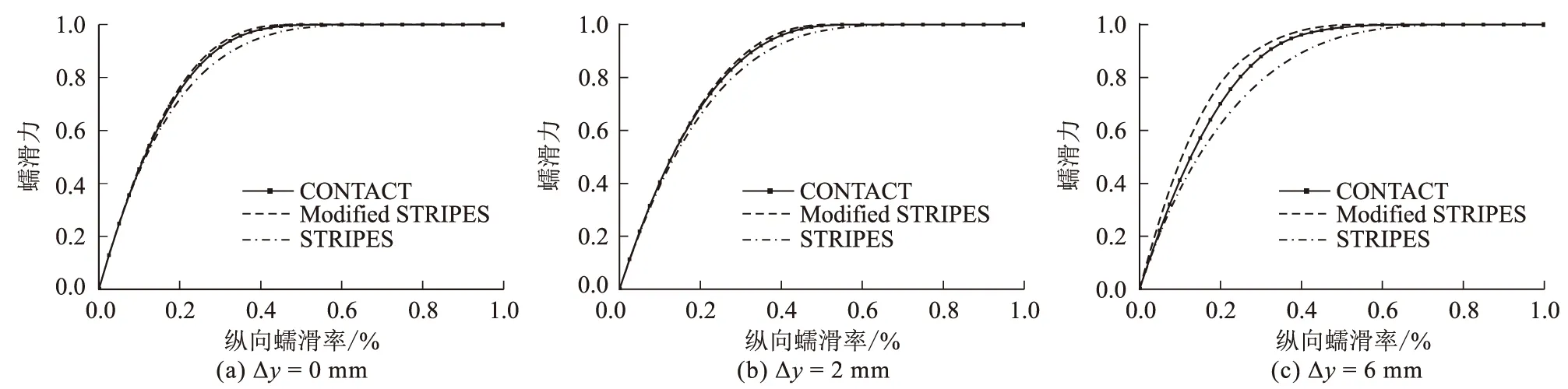
图11 纯纵向蠕滑工况不同横移量时蠕滑力的对比图

除纯蠕滑情况外，还对纯自旋条件下的蠕滑曲线进行了研究，如图12所示。与纯蠕滑情况类似，修正STRIPES模型结果更接近CONTACT计算的参考值。

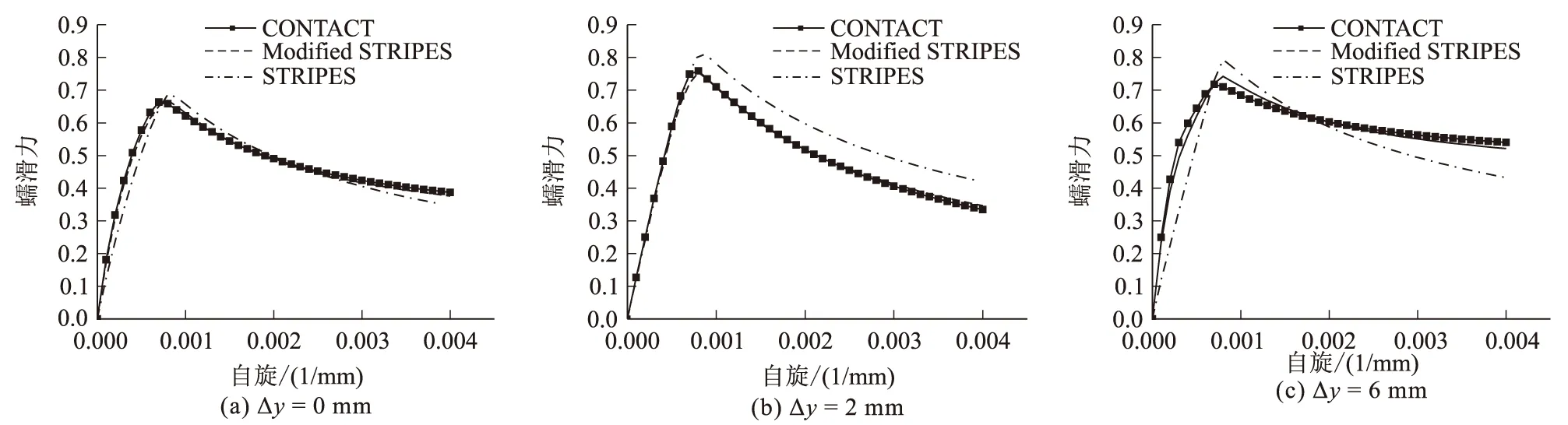
图12 纯自旋工况不同横移量下蠕滑力的对比图

5 结论

简化接触模型STRIPES已广泛应用于铁路车辆轨道动力学和轮轨接触计算，本文针对该模型提出了一些改进方法，并在修正STRIPES的模型中实现，该模型可与原模型保持相同的计算速度，并远远快于Kalker的CONTACT程序。通过与STRIPES模型和CONTACT程序计算结果进行详细比较，可得出以下结论：

(1)使用变化的渗透量比例系数替代恒定比例系数这一改进对于改善法向接触计算是必要且有效的，特别是对于整个接触区域中存在横向曲率变化的情况。

(2)本文提出了一种可靠并可广泛用于其他非赫兹接触模型的渗透迭代方法，提高了法向计算精度。

(3)在切向计算方面，改进STRIPES模型采用与FaStrip相结合的新型非椭圆方法，可显著提高剪切应力分布和蠕滑力的计算精度，并获得更加准确的蠕滑曲线。

(4)以上结果表明该方法具有更高的精确度，并可进一步应用于车辆轨道动力学和轮轨磨损计算，提高分析精度。

在下一步的研究中，本文将所提出的模型与车辆轨道动力学模型相结合，并继续深入研究其对于磨耗轮轨型面的计算精度。