Some Results on Type 2 Degenerate Poly-Fubini Polynomials and Numbers

Ghulam Muhiuddin,Waseem A.Khan,Abdulghani Muhyi and Deena Al-Kadi

1Department of Mathematics,University of Tabuk,Tabuk,Saudi Arabia

2Department of Mathematics and Natural Sciences,Prince Mohammad Bin Fahd University,Al Khobar,Saudi Arabia

3Department of Mathematics,Hajjah University,Hajjah,Yemen

4Department of Mathematics and Statistic,College of Science,Taif University,P.O.Box 11099,Taif 21944,Saudi Arabia

ABSTRACT In this paper,we introduce type 2 degenerate poly-Fubini polynomials and derive several interesting characteristics and properties.In addition,we define type 2 degenerate unipoly-Fubini polynomials and establish some certain identities.Furthermore,we give some relationships between degenerate unipoly polynomials and special numbers and polynomials.In the last section, certain beautiful zeros and graphical representations of type 2 degenerate poly-Fubini polynomials are shown.

KEYWORDS Type 2 degenerate poly-Fubini polynomials; modified degenerate polylogarithm function; unipoly functions

1 Introduction

Special functions have gained posses a considerable prominence in various fields of mathematics, physics and applied sciences (see [1–4])and the references cited therein).Some of the most worthy polynomials in the theory of special polynomials are the Fubini polynomials (see [5–7]),the type 2 poly-Fubini polynomials (see [8]), the degenerate central Fubini polynomials (see [9,10])and the new type degenerate poly-Bernoulli polynomials (see [11,12]), the degenerate poly-Cauchy polynomials (see [13]), the degenerate poly-Genocchi polynomials (see [14]).Recently, the aforementioned special polynomials and their various extensions have been widely investigated by many researchers (see [1–32])and see also each of the references cited therein.

The generating functions of the classical BernoulliBm(u), EulerEm(u)and GenocchiGm(u)polynomials are given as

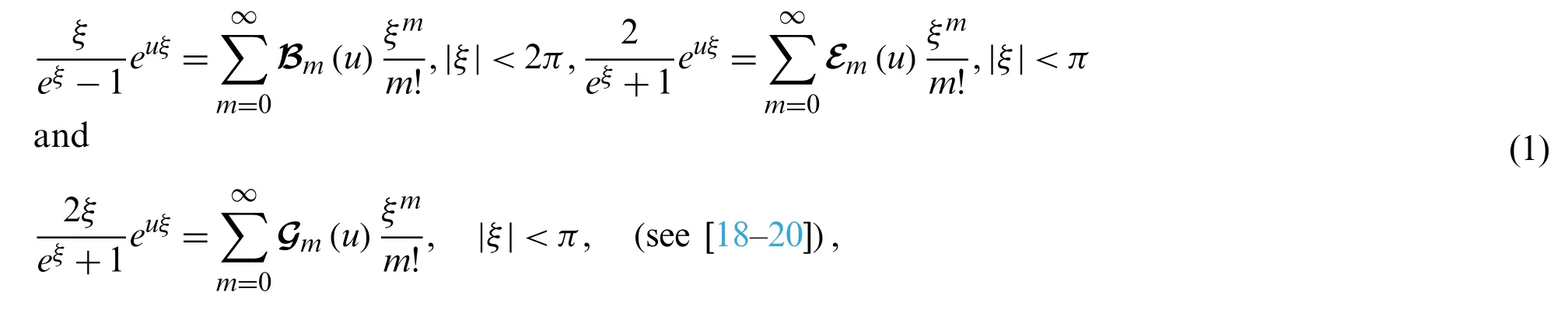
respectively.

Kargin [29] defined the 2-variable Fubini polynomials by the following generating function:

Takingu= 0 in Eq.(2), the 2-variable Fubini polynomialsFm(u,v)reduce to the classical Fubini polynomials given by

and

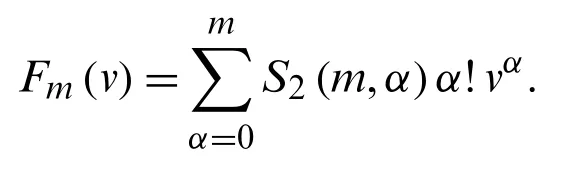
Forv= 1 in (3), we get the known Fubini numbersFm(1)=Fmas follows:

Some of the applications of Fubini polynomials and numbers can be found in [7–9,20,26,27].

The degenerate form of the exponential function is given as (see [11,12,14,22–29])

The functionis defined by the series

where the degenerate Pochhammer symbol(u)m,βis specified by

(u)m,β=u(u−β)(u−2β)···(u−(m−1)β),(u)0,β=1,(m≥1).Carlitz et al.[15,16] presented the degenerate Bernoulli polynomials as

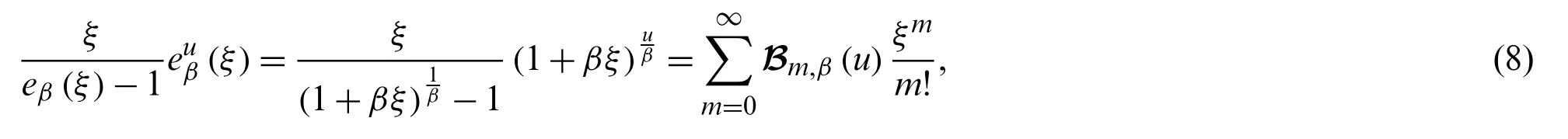
whereBm,β(0):=Bm,βdenotes degenerate Bernoulli numbers.

Forα∈Z, the modified degenerate polyexponential function [28] is defined by Kim–Kim to be

Note that

Kim et al.[14] presented the generating function of the degenerate poly-Genocchi polynomials as

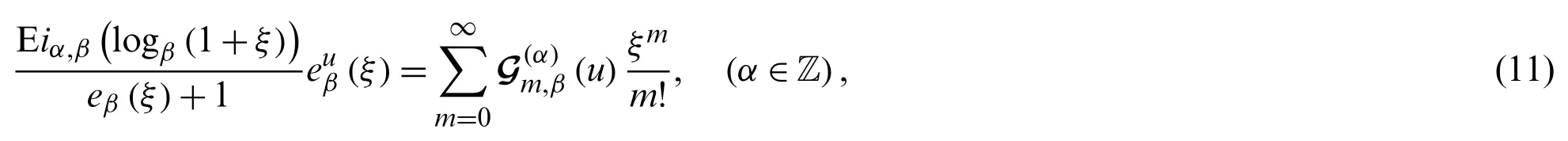
wheredenotes the degenerate poly-Genocchi numbers.

The 2-variable degenerate Fubini polynomialsFm,β(u;v)[26] are defined by

whereFm,β(0; 1):=Fm,βdenotes the degenerate Fubini numbers.

The degenerate Daehee polynomialsDm,β(u)[11] are specified by

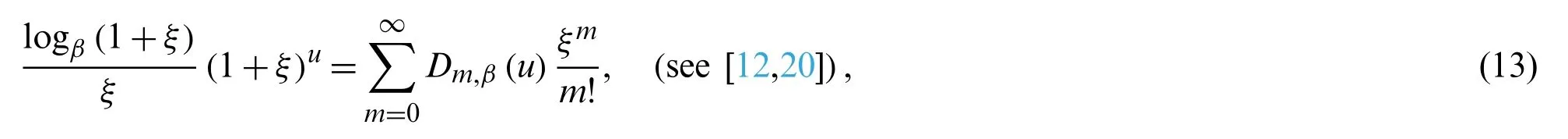
whereDm,β(0):=Dm,βdenotes the degenerate Daehee numbers.

The degenerate form of the first kind Stirling numbers are specified by

Note here that limβ→0S1,β(m,α)=S1(m,α), whereS1(m,α)are the first kind Stirling numbers given by

The degenerate form of the second kind Stirling numbers are specified by

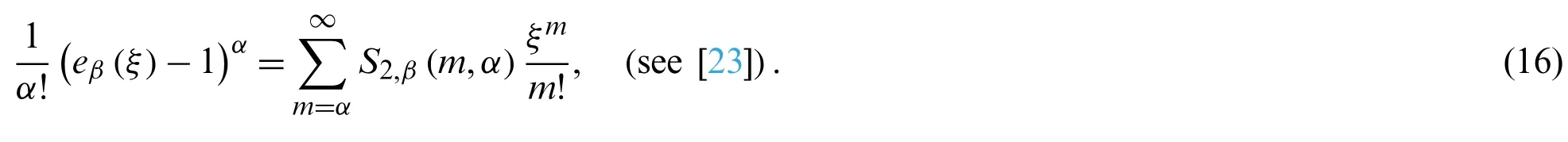
Observe here that limβ→0S2,β(m,α)=S2(m,α), whereS2(m,α)are the second kind Stirling numbers given by

The following paper is as follows.In Section 2, we define type 2 degenerate poly-Fubini polynomials via the modified degenerate polyexponential functions and obtain certain new properties related to these numbers and polynomials.In Section 3, we consider the type 2 degenerate unipoly-Fubini polynomials and discuss some identities of them.In Section 4, we find some values of type 2 poly-Fubini polynomials and draw some beautiful graphs.

2 Type 2 Degenerate Poly-Fubini Polynomials and Numbers

In the present section, we define type 2 degenerate Fubini polynomials by utilizing the modified degenerate polyexponential function and we derive some interesting relations and formulas related to these polynomials and numbers.We start the following definition as follows.

Letβ∈C andα∈Z, we consider the type 2 degenerate poly-Fubini polynomials which are defined by

Forα= 1 in Eq.(18), we get

whereFm,β(u;v)denotes the degenerate Fubini polynomials (see Eq.(12)).

Obviously

Thus, by (18)and (20), we have

where;v)denotes the type 2 poly-Fubini polynomials (see [28]).

Theorem 2.1.Form≥0.Then, we have

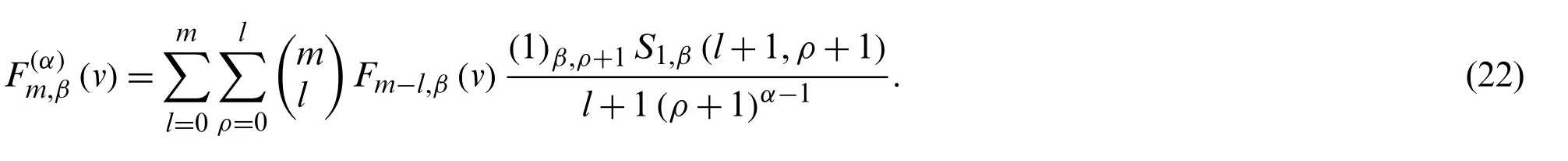
Proof.By using Eqs.(9), (14)and (18), we observe that

Therefore, by (23), we obtain the result.

Corollary 2.1.Form≥0.Then, we have

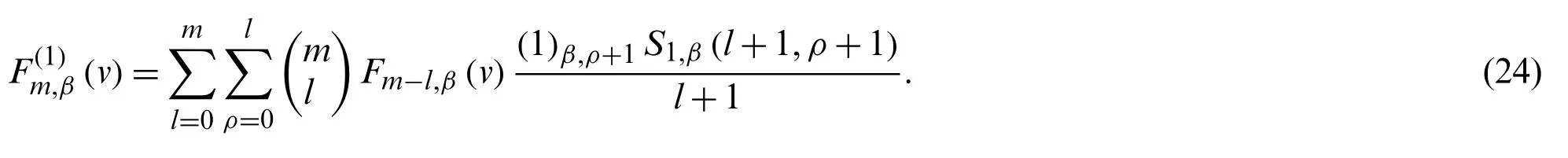
Theorem 2.2.Letm≥0.Then, we have

Proof.From (18), we observe that

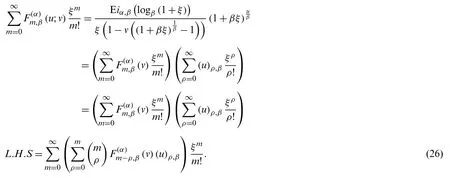
By comparing the coefficients on both sides of Eq.(26), we reach at the following result (25).

In [12], it is well known that the degenerate second kind Bernoulli polynomials are defined by

wherebm,β(0):=bm,βdenotes the degenerate second kind Bernoulli numbers.

Theorem 2.3.Form≥0, we have

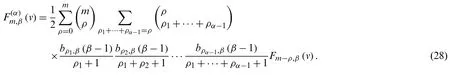
Proof.From (9), it follows that

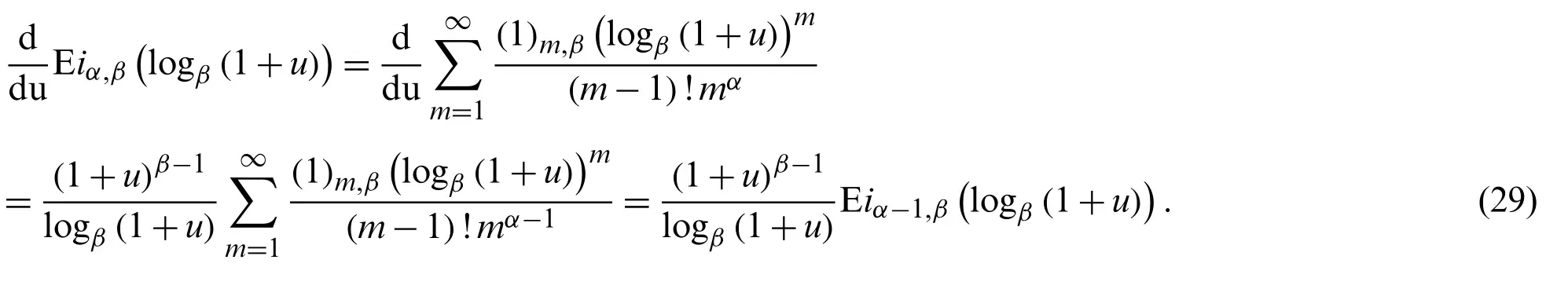
Thus, from (18)and (29), we have

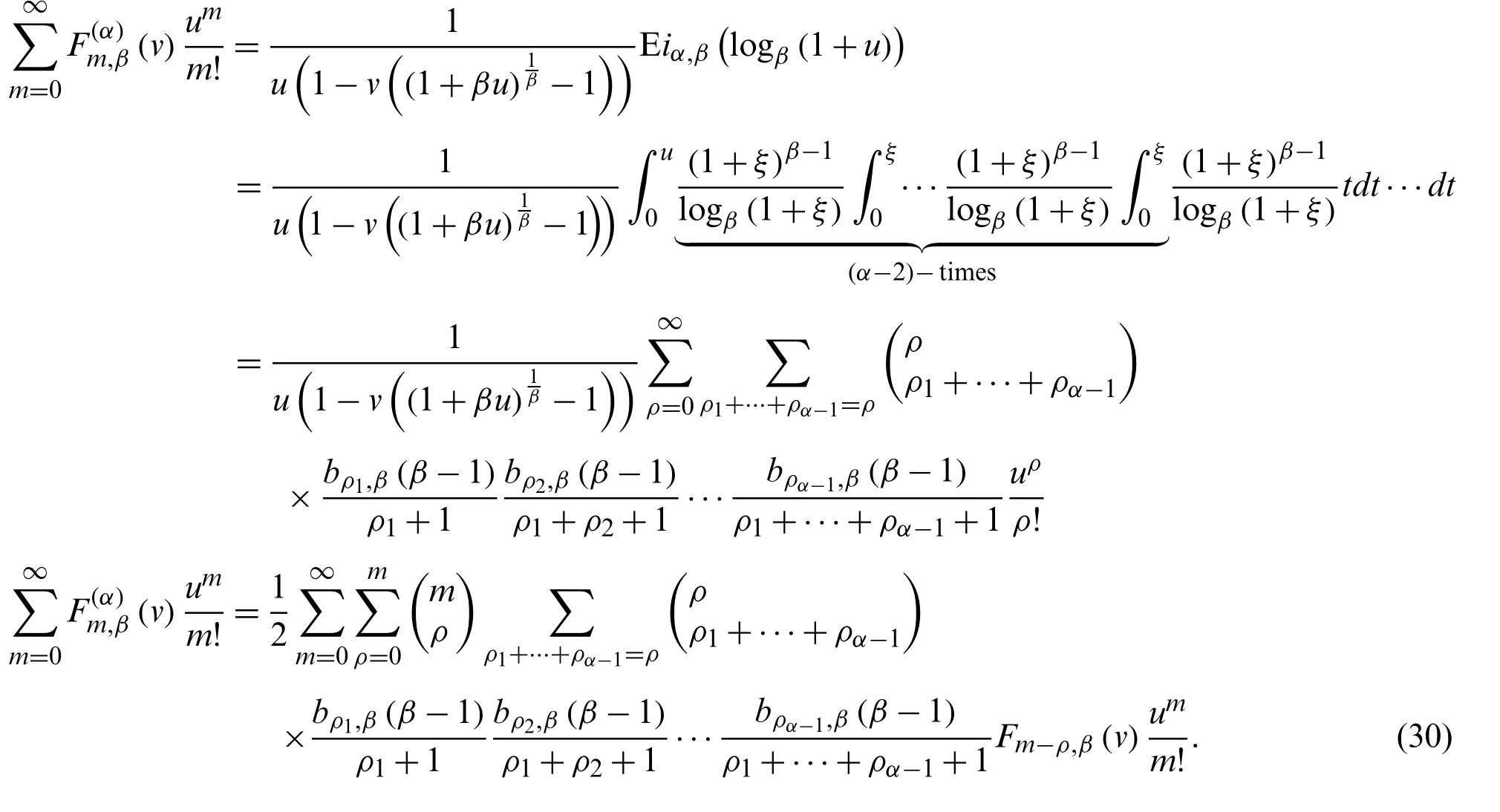
Therefore, by (30), we obtain the result.

Corollary 2.2.Forα≥2, we have

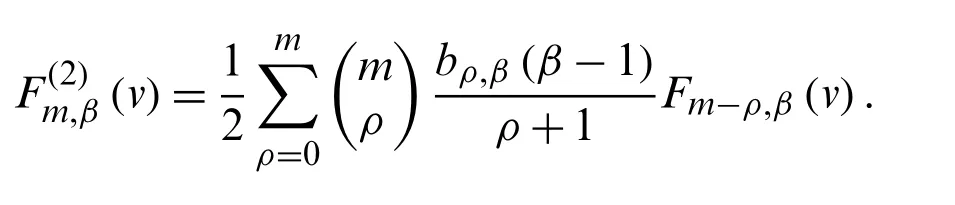
Theorem 2.4.Letα≥1 andα∈N ∪{0},s∈C, we have

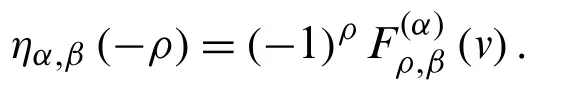
Proof.Letα≥1, be an integer.Fors∈C, we define the functionηα,β(s)as

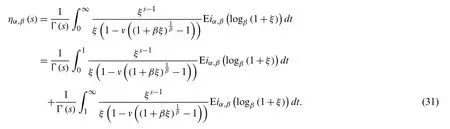
Here, we note that the second integral converges absolutely for anys∈C, then the second term on the r.h.s.vanishes at non-positive integers.Hence,

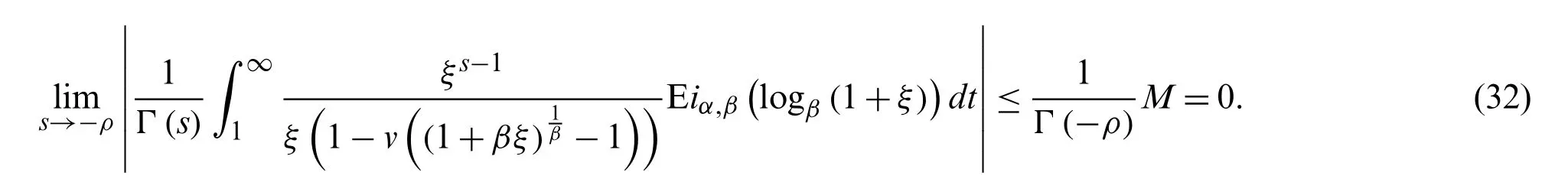
Also, for ℜ(s)> 0, the first integral in (32)can be written as

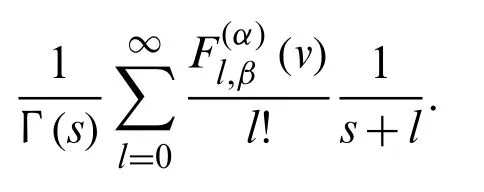
Using (31)and (32), we see that

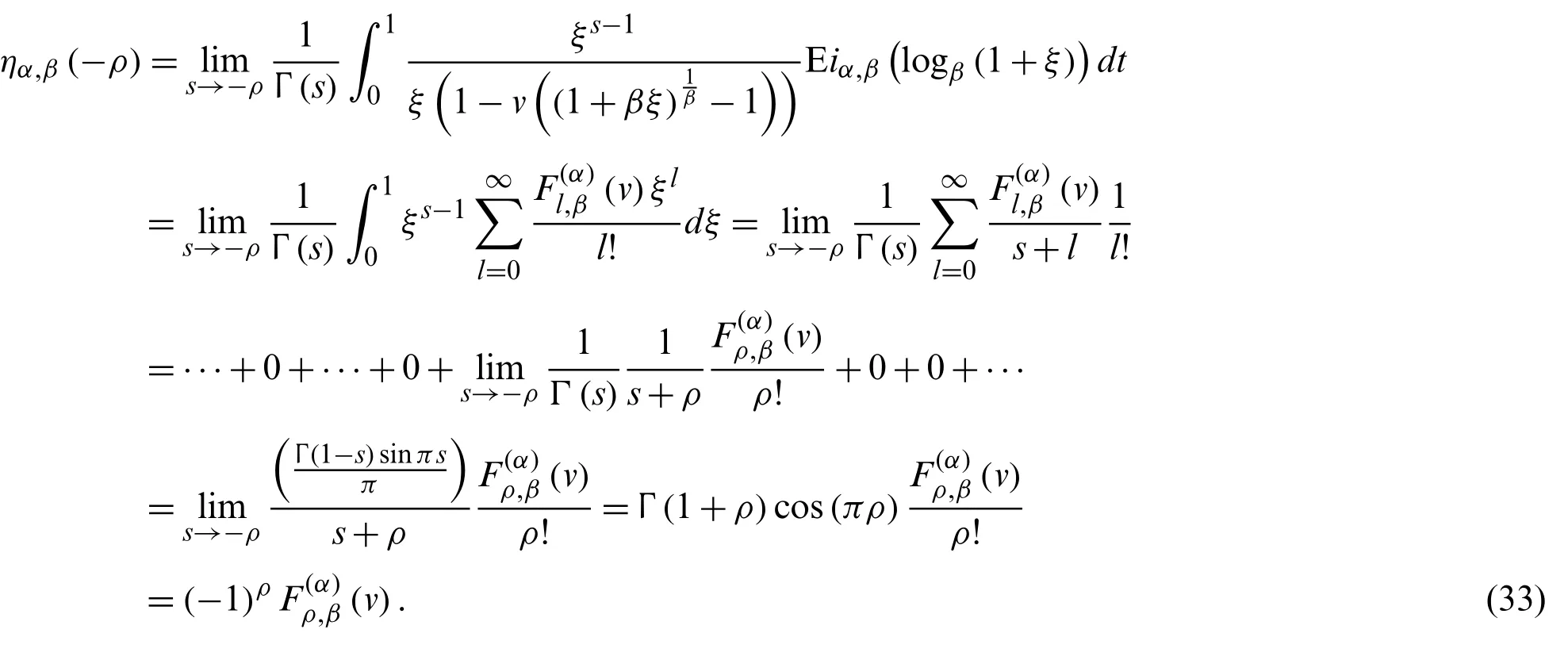
Therefore, by (33), the result is obtained.

Theorem 2.5.Letα≥1 andρ∈N ∪{0},s∈C, we have

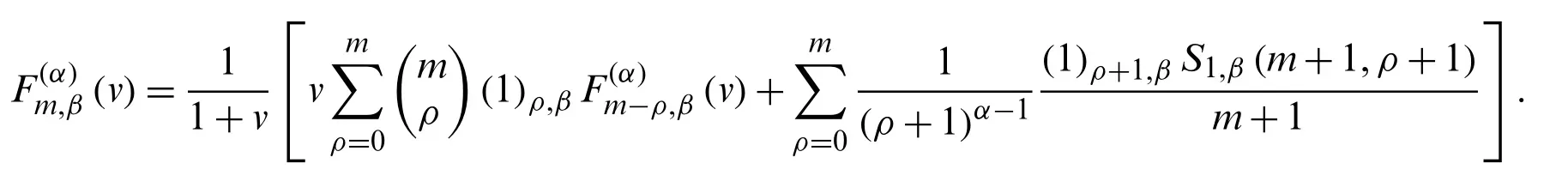
Proof.From (18), we note that

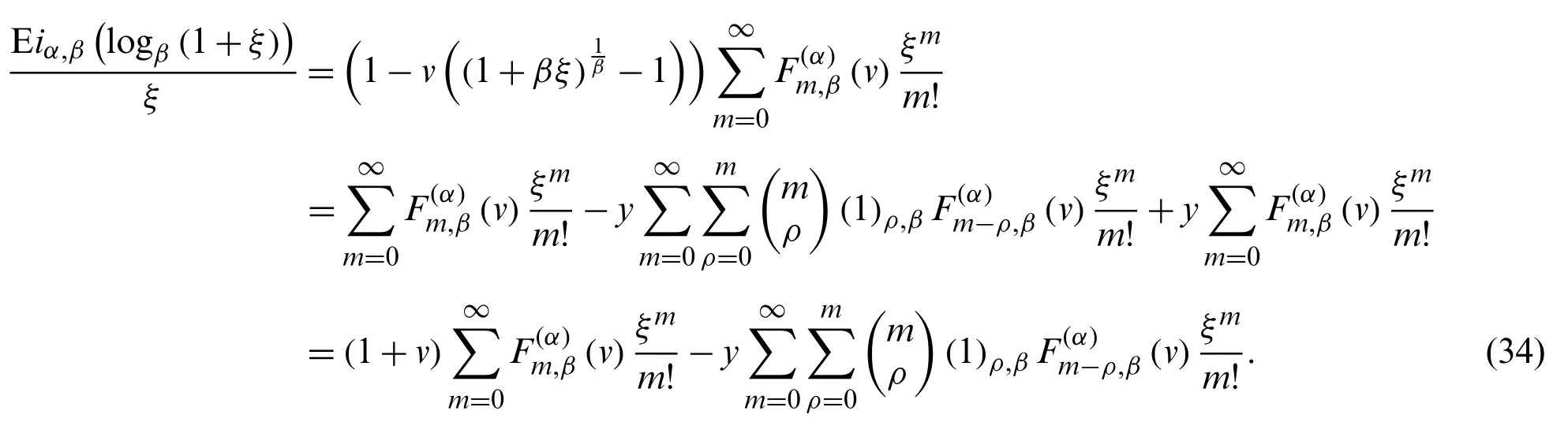
On the other hand,

Therefore, by (34)and (35), we reach at the desired result.

Forα= 1 in Theorem 2.5., the following corollary is obtained.

Corollary 2.3.Forρ∈N ∪{0}, we have

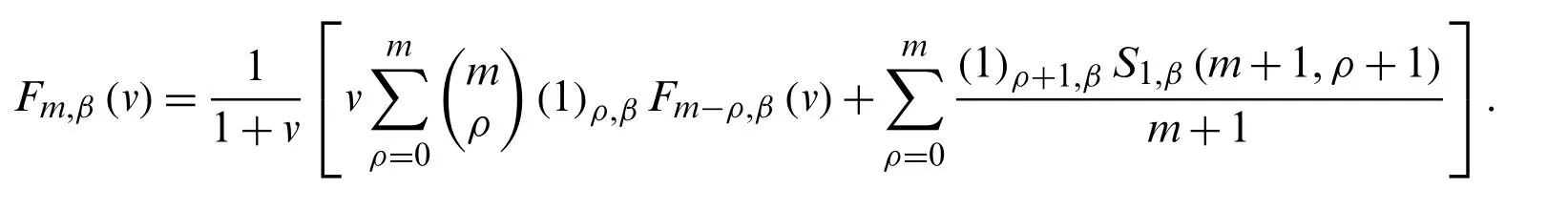
Theorem 2.6.Letm≥0.Then, we have

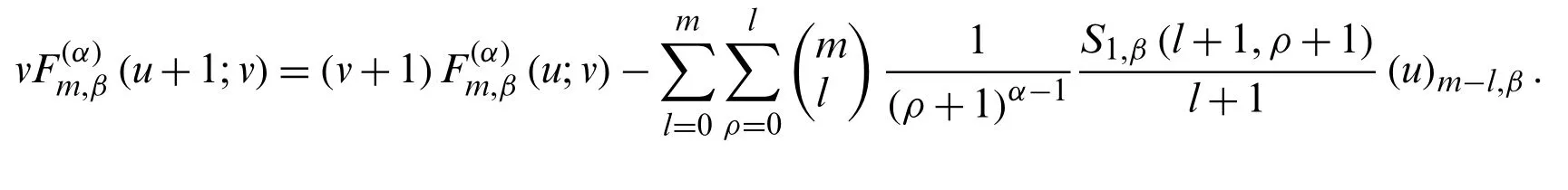
Proof.From (18), we note that

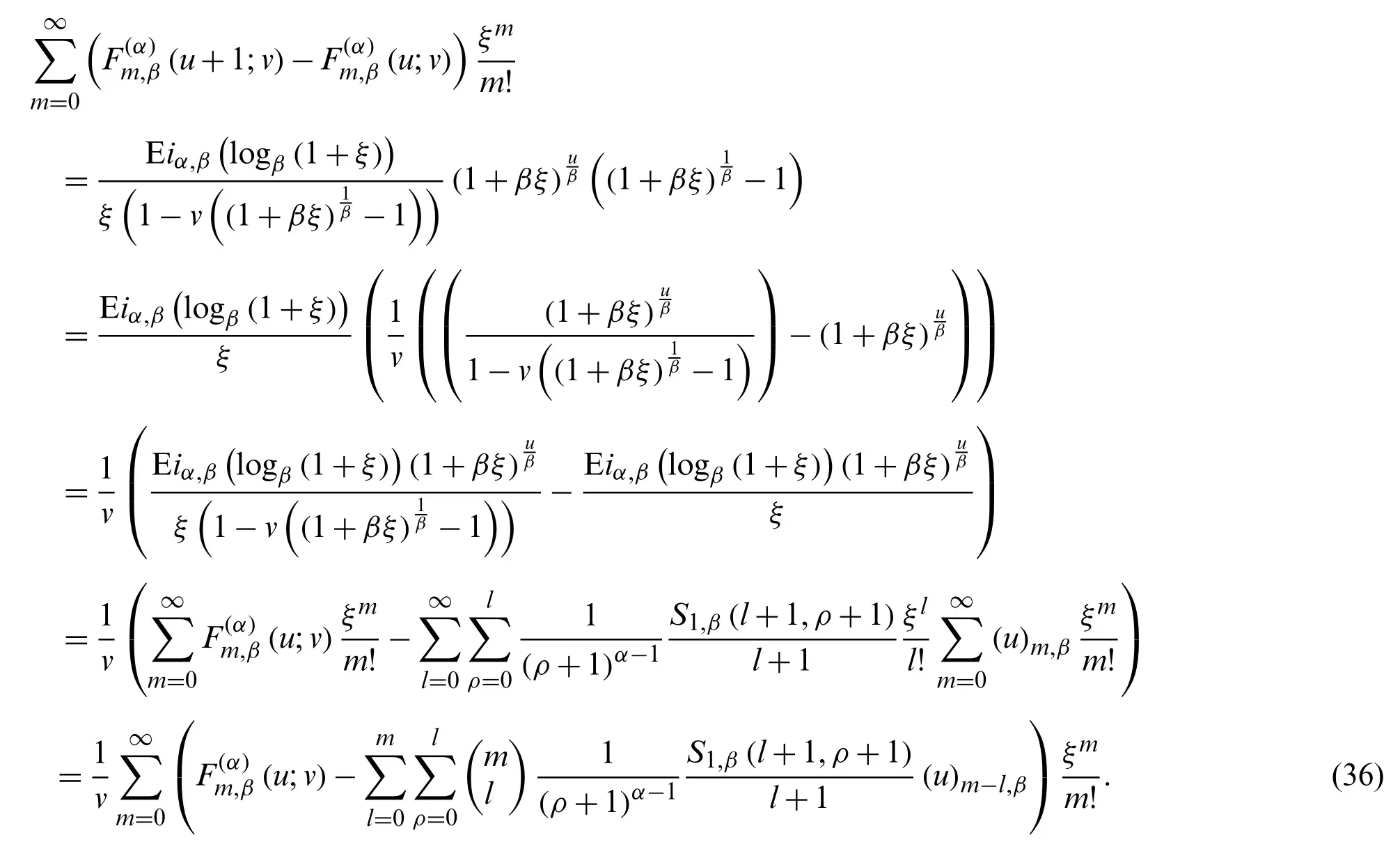
Upon comparing the coefficients ofof the above equation, we get the result.

Whenu= 0 andu=−1 in Theorem (2.6), we get

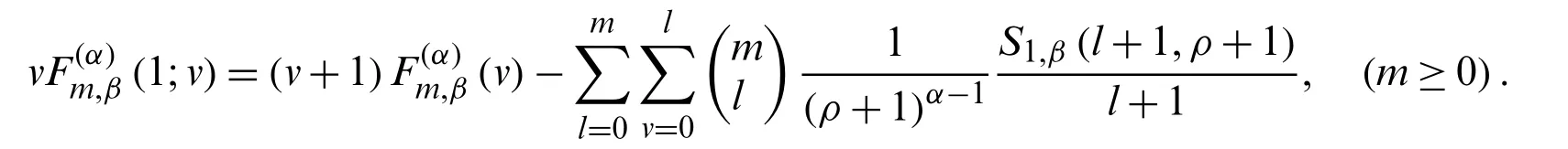
and

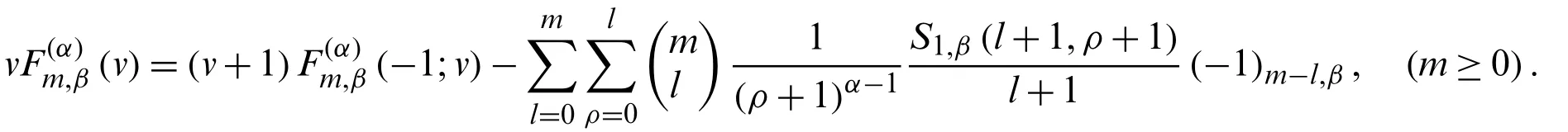
Theorem 2.7.Letm≥0.Then, we have

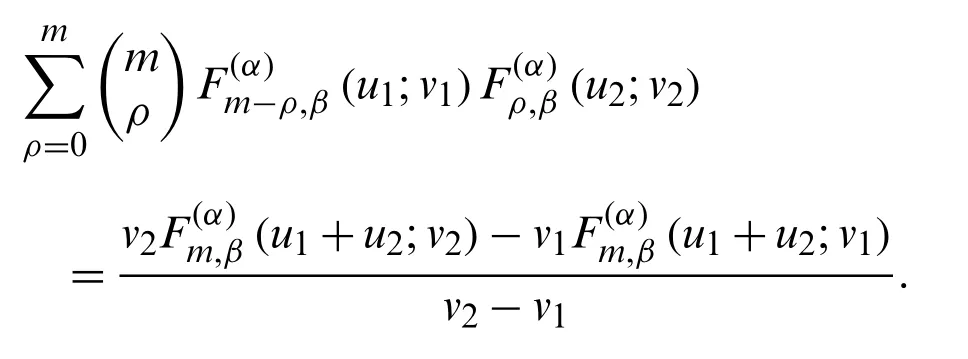
Proof.Now, we observe that

Therefore, by (37)and (38), we get the result.

Foru1=u2= 0 in Theorem 2.7, we have

Corollary 2.4.Letα∈Z andm≥0, we have

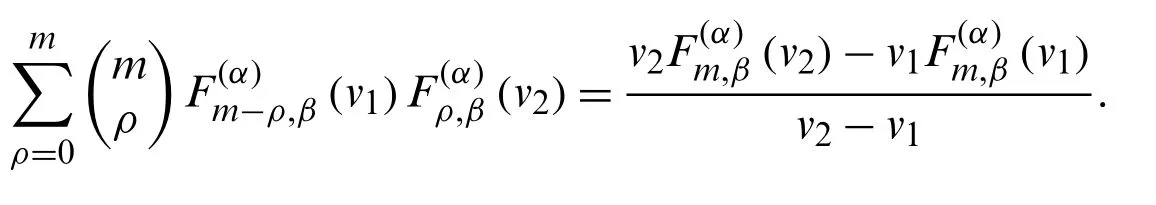
Theorem 2.8.Letm≥0.Then, we have

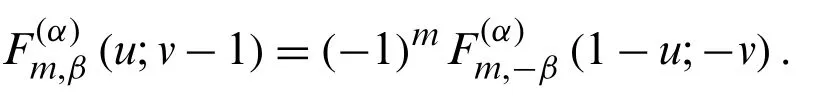
Proof.From (18), we note that

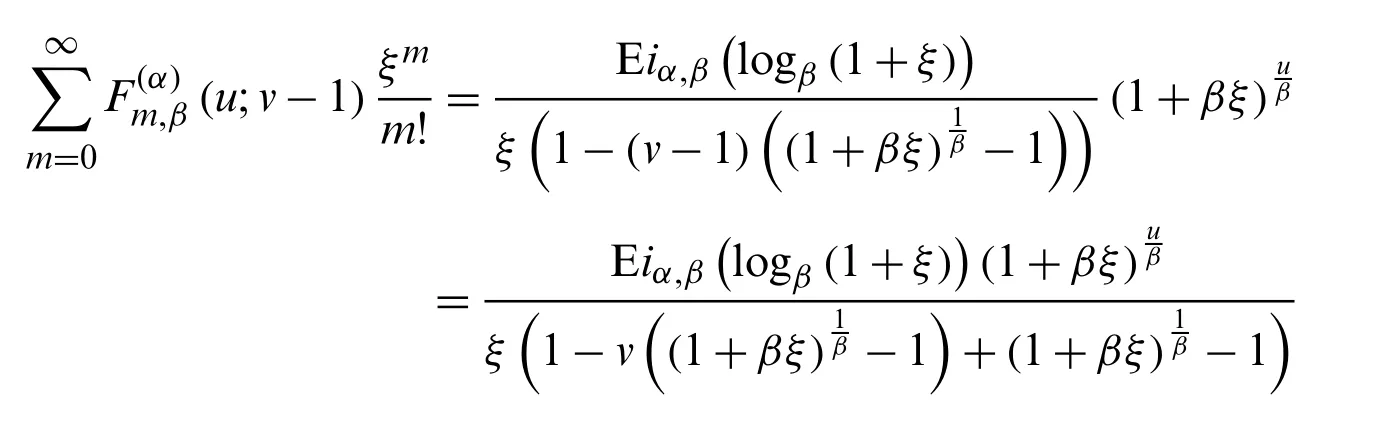
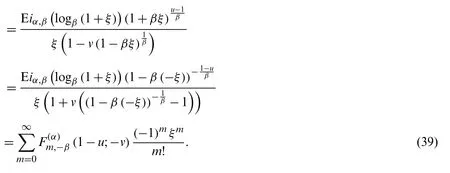
Comparing the coefficients ofof the above equation, we obtain the result.

Adjustingu= 0 in Theorem 2.8, we get

Corollary 2.5.Letα∈Z andm≥0, we have

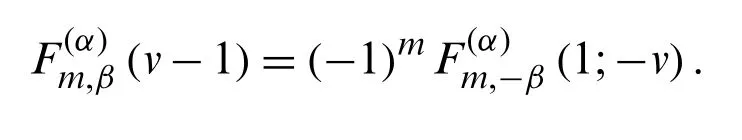
Theorem 2.9.Letα∈Z andm≥0, we have

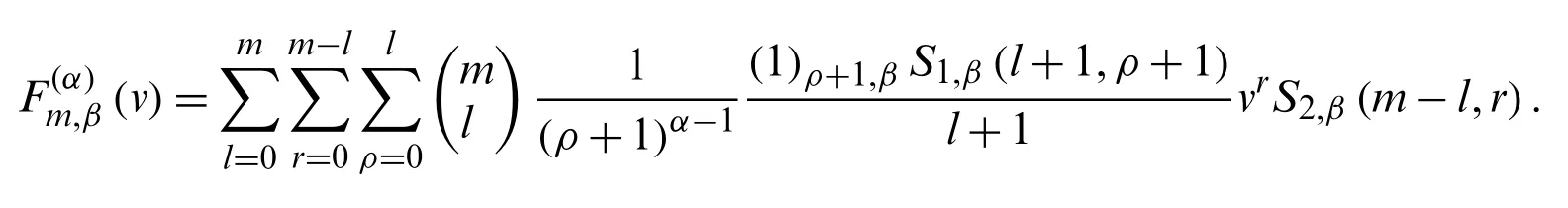
Proof.From (18), we see that

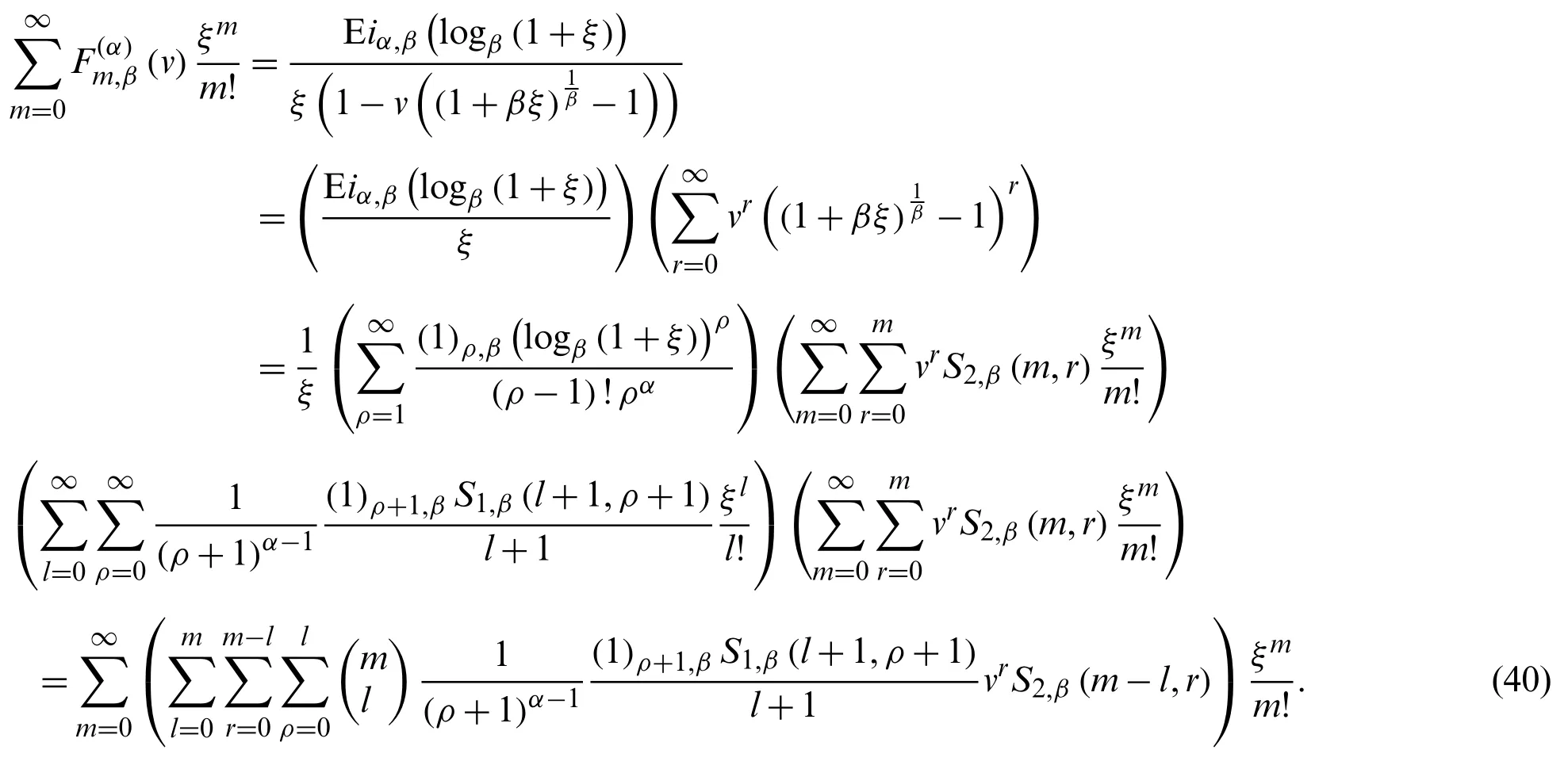
Therefore, utilizing Eqs.(40), the result is obtained.

Corollary 2.6.Letα∈Z andm≥0, we have

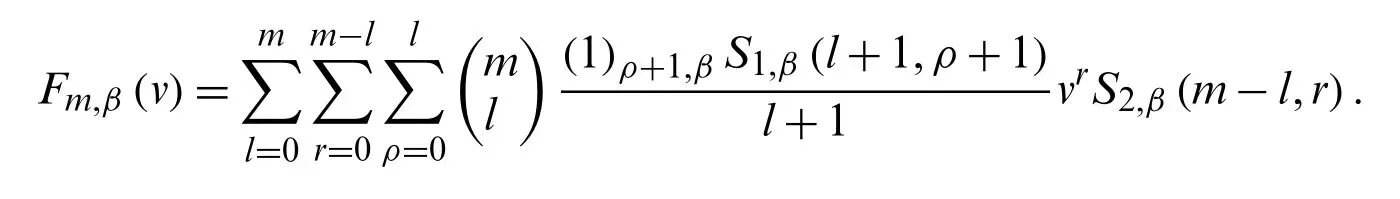
In the next section, the type 2 degenerate unipoly-Fubini polynomials are established and,certain explicit expressions and properties are obtained.

3 Type 2 Degenerate Unipoly-Fubini Polynomials and Numbers

Recently, Kim et al.[22] defined the unipoly function by

wherepdenotes any real or complex valued arithmetic function which is a defined on N (set of positive integers).

Moreover,

denotes the ordinary polylogarithm function.

Dolgy et al.[13] introduced the degenerate unipoly function attached to polynomialsp(u)as follows:

We note that

is the modified degenerate polyexponential function.

By using (43), we introduce the degenerate unipoly-Fubini polynomials as follows:

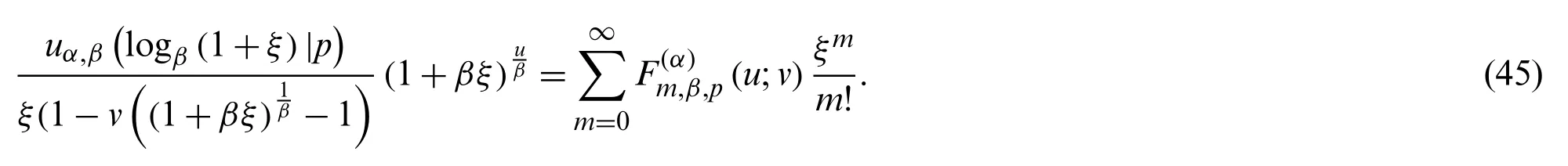
In the case whenu= 0 andy= 1,are called the type 2 degenerate unipoly-Fubini numbers.

Theorem 3.1.Letm≥0.Then, we have

Proof.Let us takep(m)=Then we have

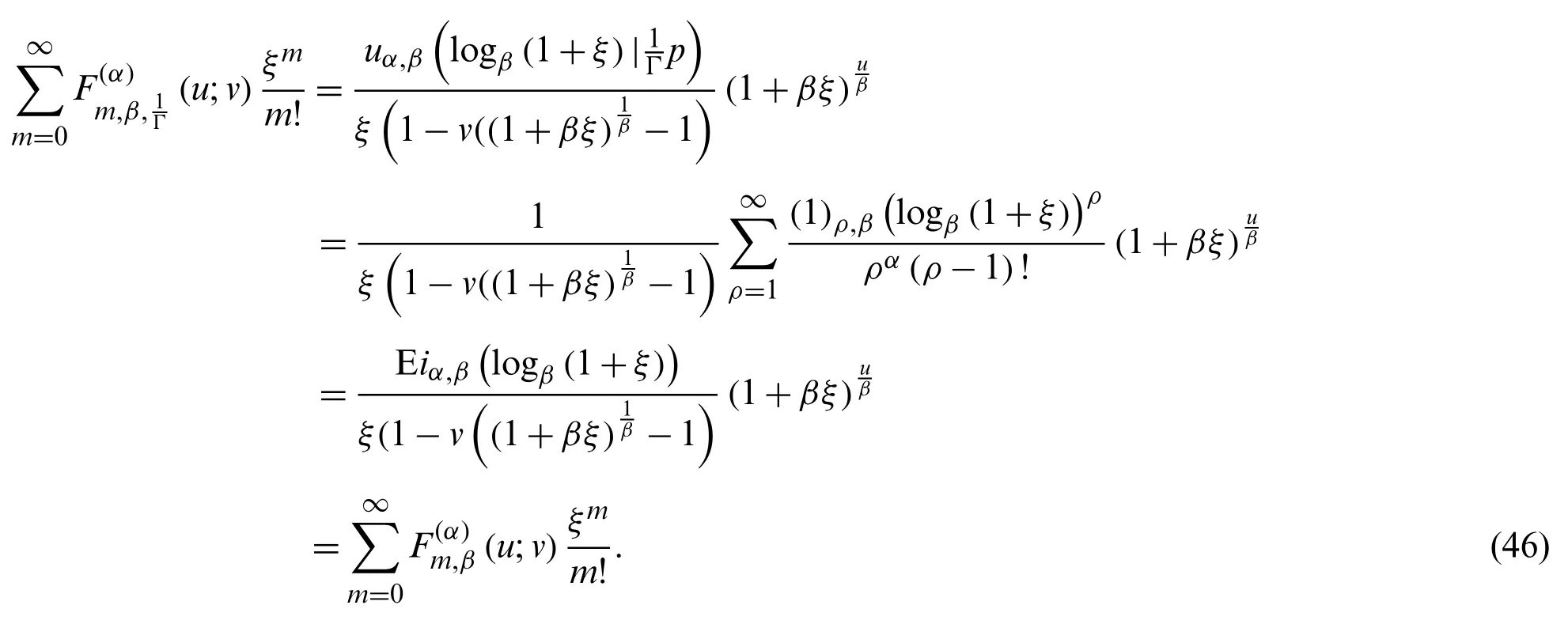
Thus, by (46), the result is obtained.

Theorem 3.2.Form∈N andα∈Z, we have

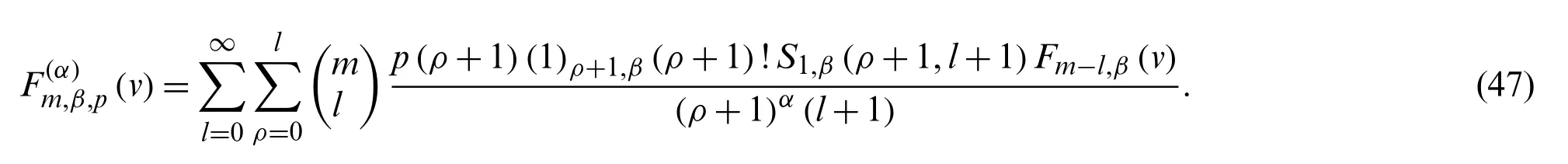
Proof.From (45), we get

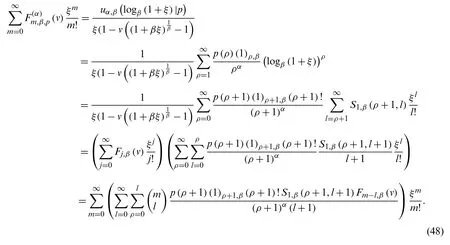
Thus, we complete the proof of this theorem.

In particular,

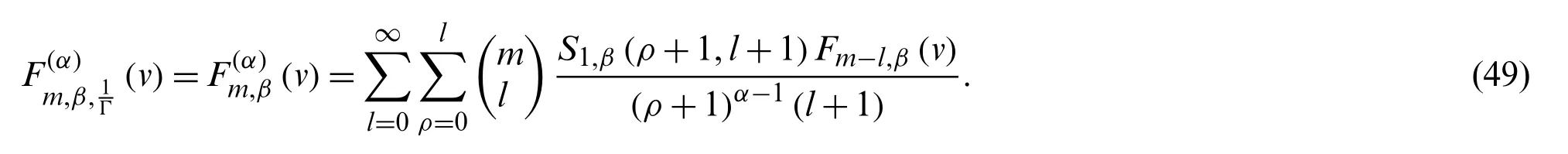
Theorem 3.3.Letm≥0 andα∈Z.Then we have

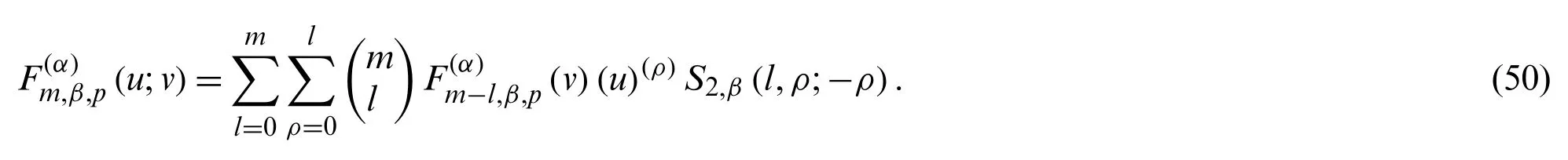
Proof.From (45), we observe that

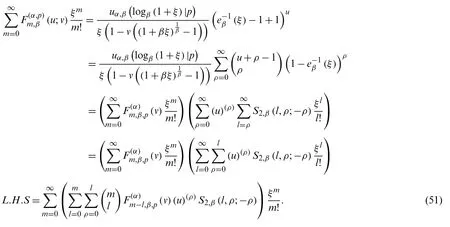
By (51), we obtain the result.

Theorem 3.4.Form≥0 andα∈Z, we have

Proof.From (45), we observe that

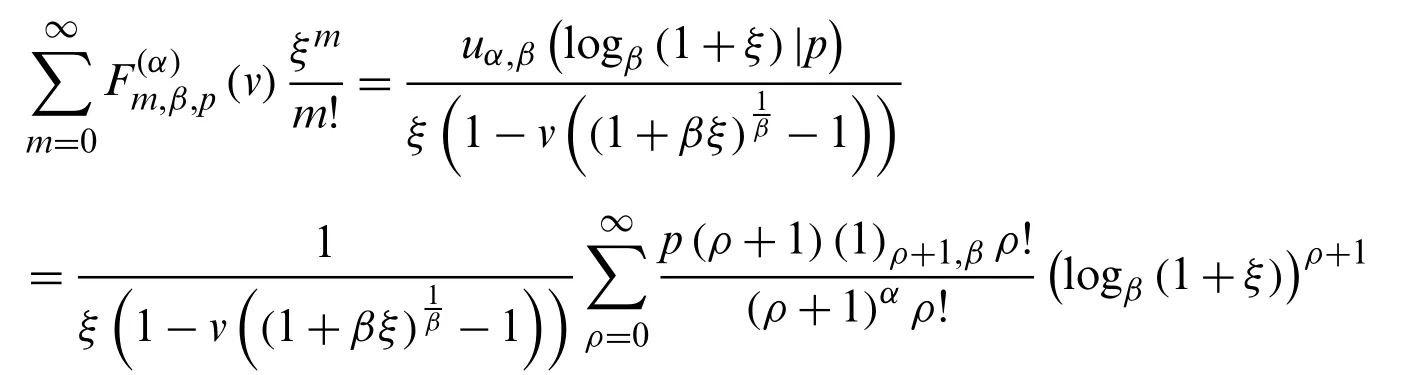
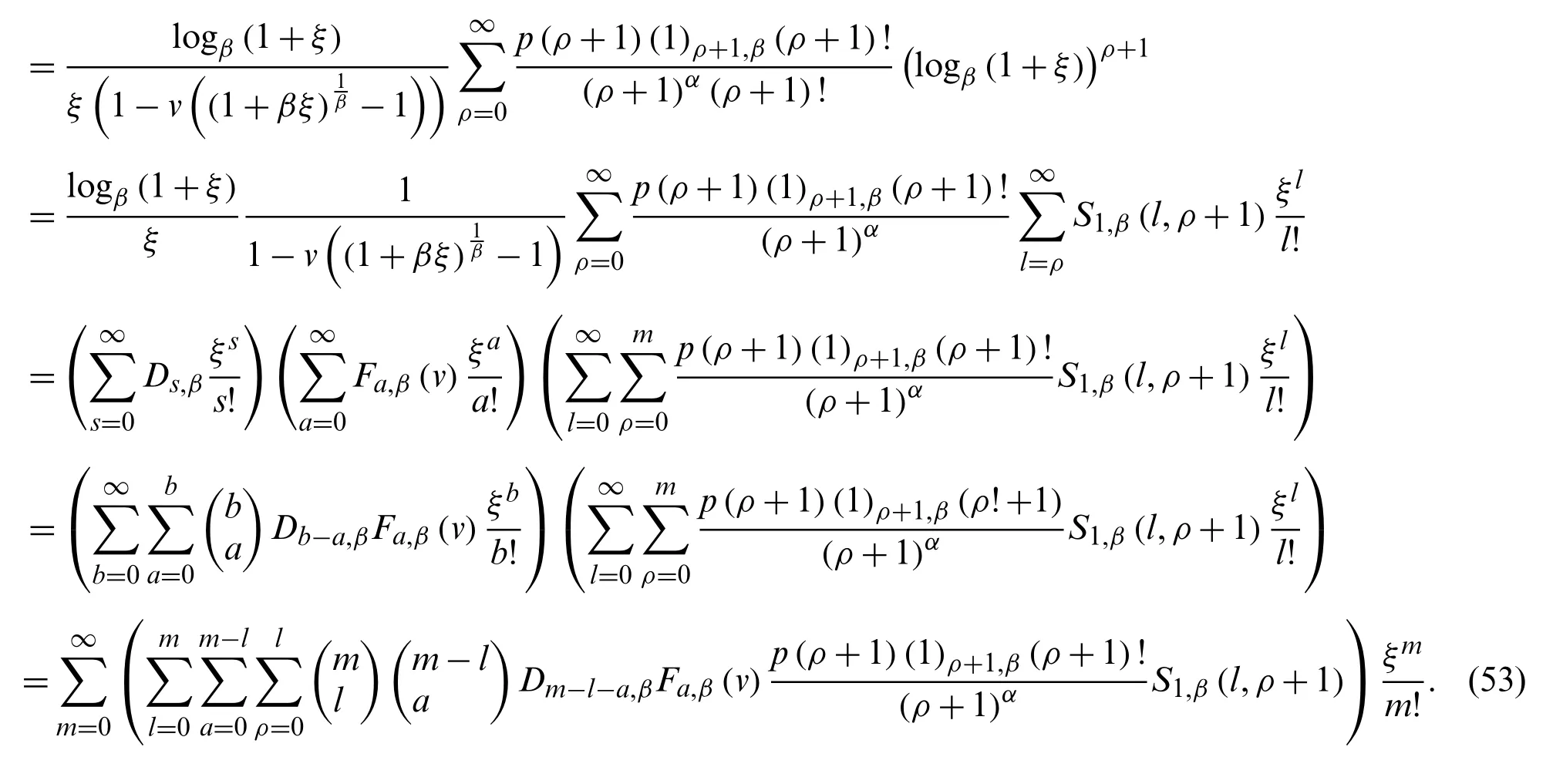
Comparing the coefficients ofof the above equation, the result is established.

Theorem 3.5.Form≥0 andα∈Z, we have

Proof.Applying the difference operator △βon both sides of Eq.(45), gives

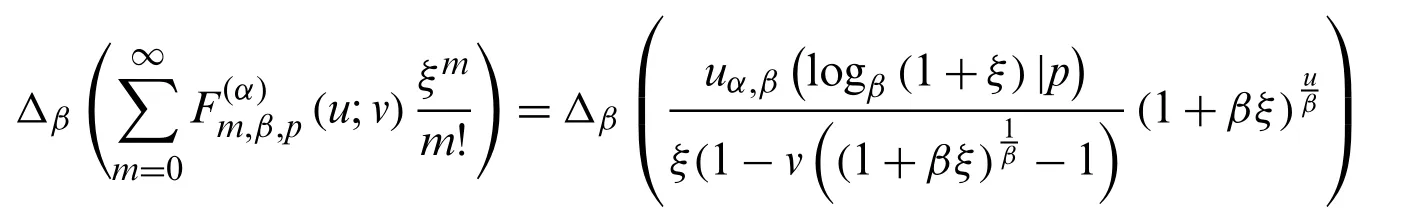
and then we have

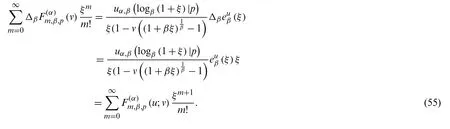
Therefore, by (55), we obtain the result.

Theorem 3.6.Letm≥0 andα∈Z.Then we have

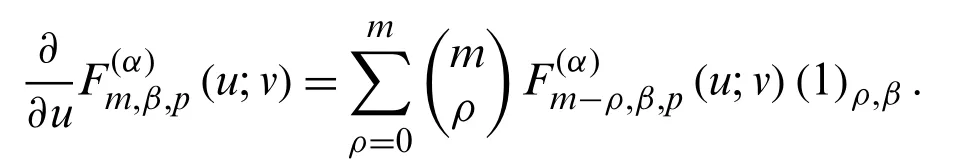
Proof.Applying the operatorin both sides of (45), we have

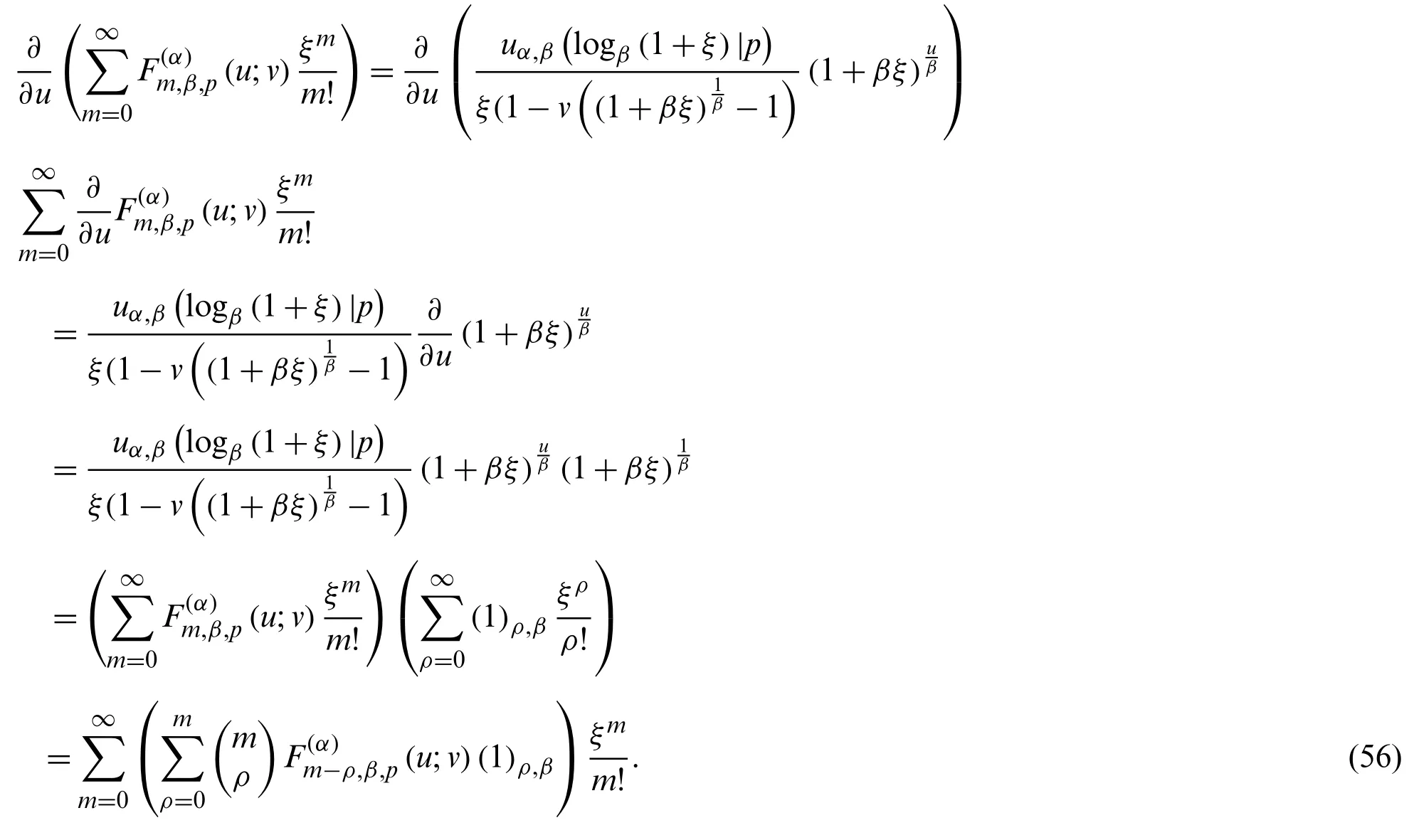
In view of (56), we complete the proof.

4 Computation of Zeros and Graphical Representation

To understand the structure of the type 2 degenerate poly-Fubini polynomialswe employ some numerical investigations (usingMathematica)to examine properties of figures, look and to discover some interesting patterns.First, we give few(forα= 5,β= 4)as follows:

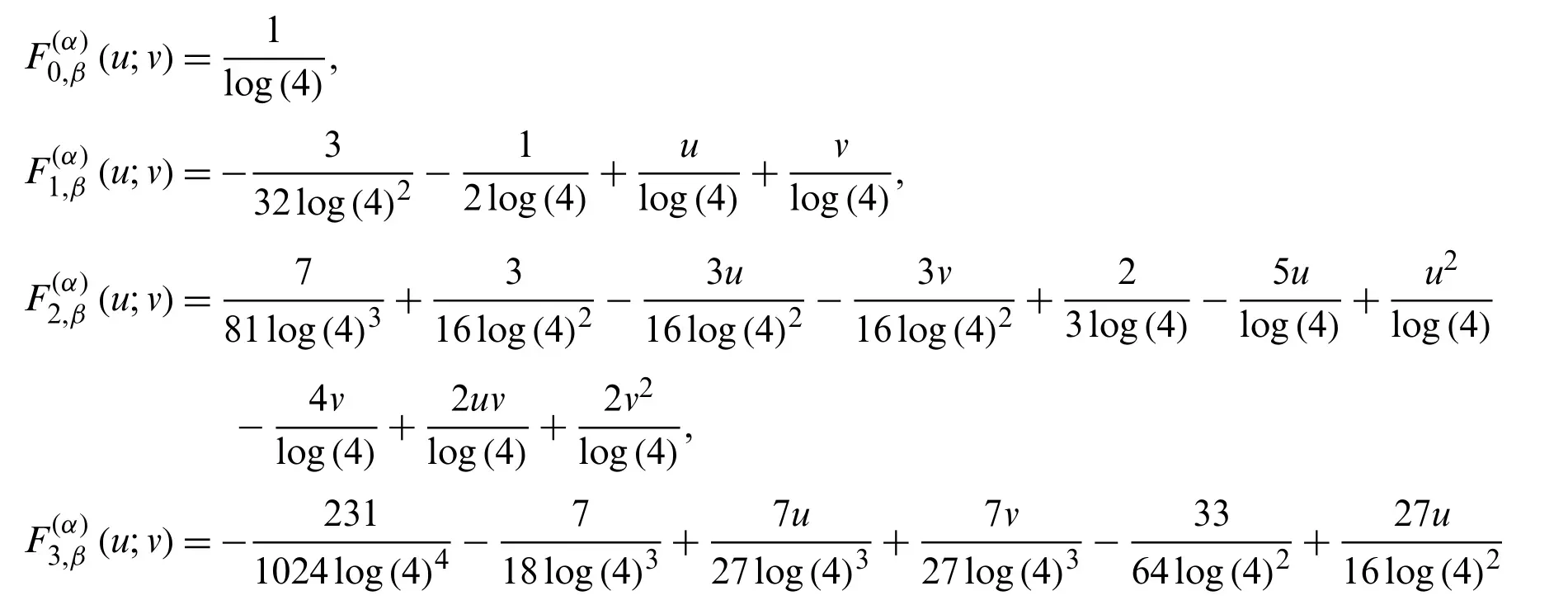
Next, we display the shape offor v = 4, −100 ≤u ≤ 100 in Fig.1, for m= 1, 2, ..., 8.

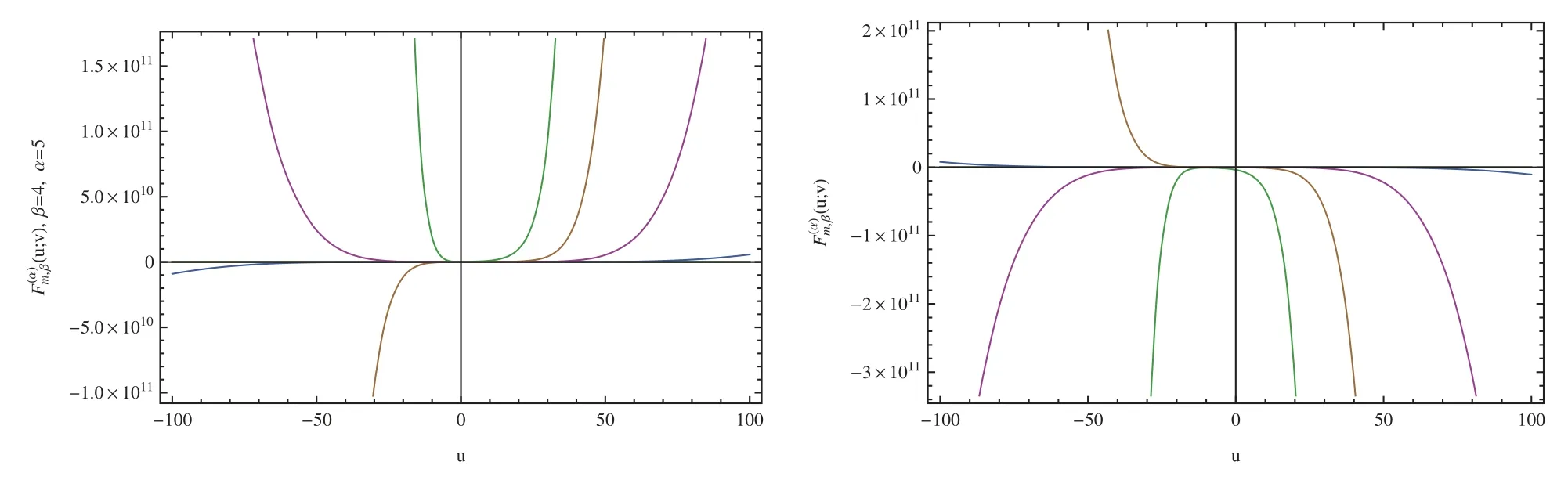
Figure 1: Graphs of (u;v)(for α= 5, β= 4 (left)and α=7, β= (right))

The real and complex zeros of=0 for v= 4, α= 5, β= 4 are listed in Tab.1.

Table 1: Approximate solution of (u;v)

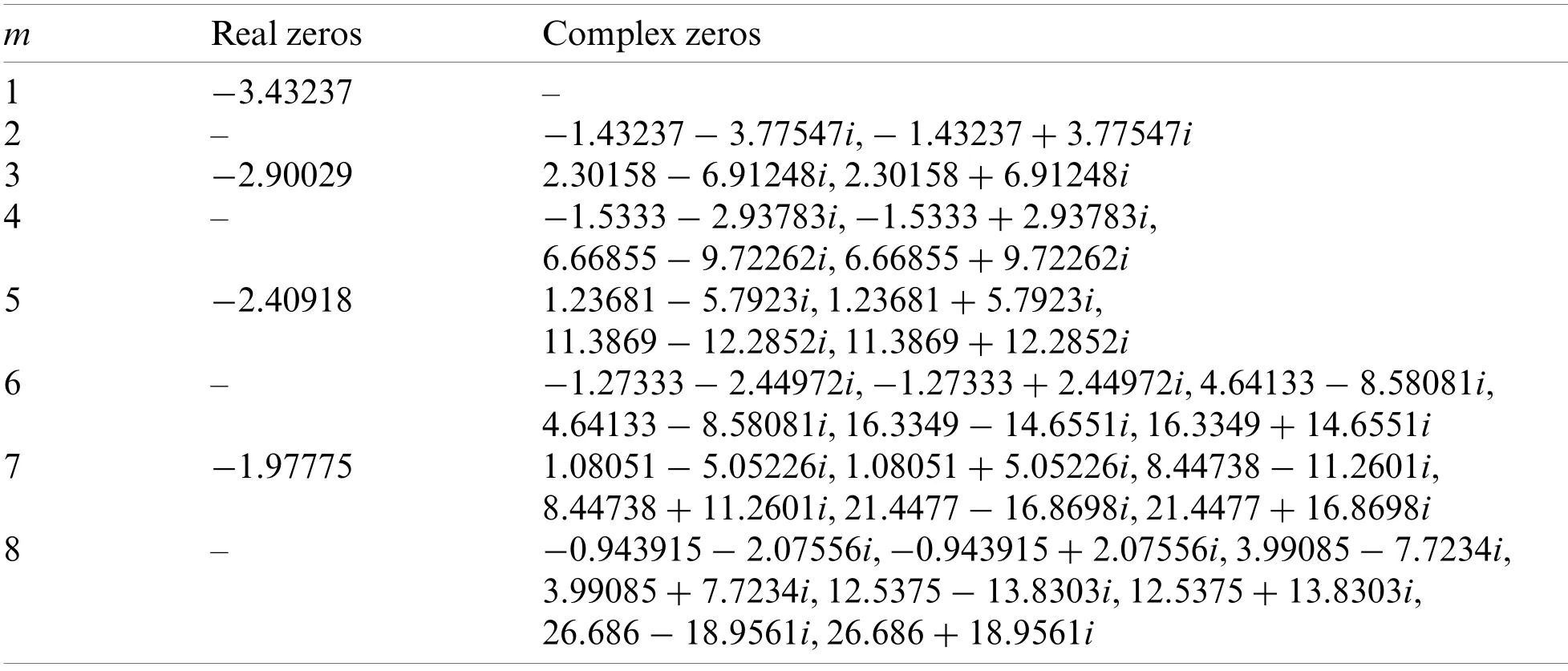
Table 1: Approximate solution of (u;v)

m Real zeros Complex zeros 1−3.43237 –2–−1.43237 −3.77547i,−1.43237+3.77547i 3−2.90029 2.30158 −6.91248i,2.30158+6.91248i 4–−1.5333 −2.93783i,−1.5333+2.93783i,6.66855 −9.72262i,6.66855+9.72262i 5−2.40918 1.23681 −5.7923i,1.23681+5.7923i,11.3869 −12.2852i,11.3869+12.2852i 6–−1.27333 −2.44972i,−1.27333+2.44972i,4.64133 −8.58081i,4.64133 −8.58081i,16.3349 −14.6551i,16.3349+14.6551i 7−1.97775 1.08051 −5.05226i,1.08051+5.05226i,8.44738 −11.2601i,8.44738+11.2601i,21.4477 −16.8698i,21.4477+16.8698i 8–−0.943915 −2.07556i,−0.943915+2.07556i,3.99085 −7.7234i,3.99085+7.7234i,12.5375 −13.8303i,12.5375+13.8303i,26.686 −18.9561i,26.686+18.9561i

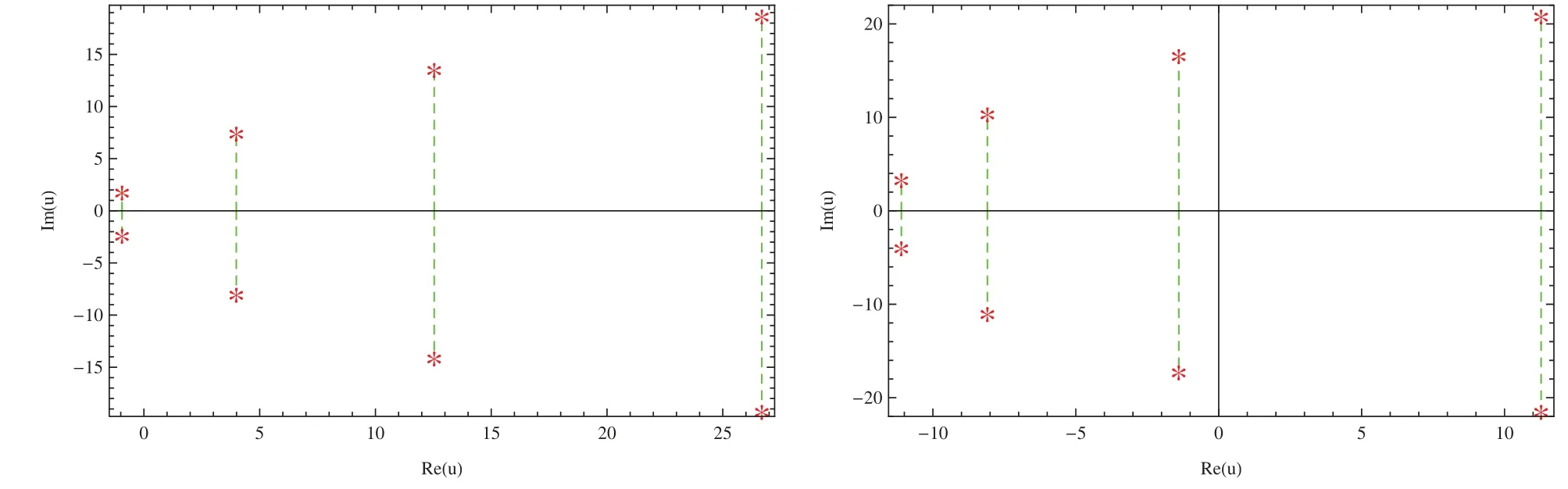
Figure 2: Zeros of u;v) (for α= 5, β= 4 (left)and α=7,β=(right))

The stacking structure of approximate roots of=0 forv= 4,m= 1, 2,..., 8 is given in Fig.3.

Figure 3: Stacking structure of approximate roots of (for α= 5, β = 4 (left)and α=7,β(right))

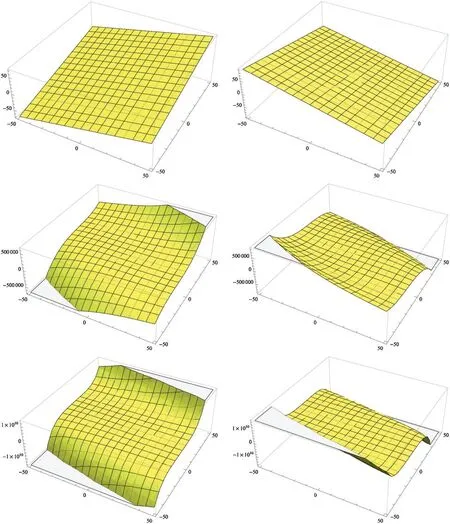
To provide more clear explanation of the structure of the 2 degenerate poly-Fubini polynomialswe present the 3D surface for some values ofm, these surfaces are displayed in Fig.4.

Figure 4: Surface plot of (u;v), m= 1, 3, 5, 8 (for α= 5, β= 4 (left)and α=7,β=(right))

5 Conclusions

In this article, we have introduced type 2 degenerate poly-Fubini polynomials and established certain identities of these numbers and polynomials.Further, we defined the degenerate unipoly-Fubini polynomials and derived certain properties of these numbers and polynomials and given multifarious relations including derivative and integral properties.In addition, we have provided relationships between degenerate unipoly-Fubini polynomials and degenerate special polynomials.In the last section, we have these polynomials with the help of Mathematica.

Acknowledgement:The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement:This work was supported by the Taif University Researchers Supporting Project (TURSP-2020/246), “Taif University, Taif, Saudi Arabia”.

Conflicts of Interest:The authors declare that they have no conflict of interest to report regarding the present study.