An Improved Method Based on TODIM and TOPSIS for Multi-Attribute Decision-Making with Multi-Valued Neutrosophic Sets

Dongsheng Xu and Lijuan Peng

School of Science,Southwest Petroleum University,Cheng du,610500,China

ABSTRACT Due to the complexity of decision-making problems and the subjectivity of decision-makers in practical application, it is necessary to adopt different forms of information expression according to the actual situation of specific decision-making problems and choose the best method to solve them.Multi-valued neutrosophic set,as an extension of neutrosophic set,can more effectively and accurately describe incomplete,uncertain or inconsistent information.TODIM and TOPSIS methods are two commonly used multi-attribute decision-making methods,each of which has its advantages and disadvantages.This paper proposes a new method based on TODIM and TOPSIS to solve multi-attribute decision-making problems under multi-valued neutrosophic environment.After introducing the related theory of multi-valued neutrosophic set and the traditional TODIM and TOPSIS methods,the new method based on a combination of TODIM and TOPSIS methods is described.And then,two illustrative examples proved the feasibility and validity of the proposed method.Finally,the result has been compared with some existing methods under the same examples and the proposed method’s superiority has been proved.This paper studies this kind of decision-making problem from algorithm idea,algorithm steps and decision-making influencing factors.

KEYWORDS Multi-valued neutrosophic set; TODIM; TOPSIS; multi-attribute decision-making

1 Introduction

Multi-attribute decision-making (MADM)problem refers to how to rank alternatives and select the optimal one when the decision-making problem contains multiple attributes.As an important part of modern decision-making science, it has made significant progress and wide application since the early 1960s.Its methodology and theory have been applied to many fields,such as investment decision-making [1,2], project evaluation [3], personnel management [4], supplier selection [5–8], medical equipment selection [9,10], and urban sustainability assessment [11],etc.

A complete MADM process mainly consists of two core parts: representation of decision information and integration of decision information.The representation of decision information refers to using correct language to express decision information correctly.Due to the complexity of the objective problems and the vagueness of the subjective thinking of decision makers in practical applications, it is difficult for decision makers to give accurate evaluation values for MADM problems with inaccurate, uncertain or incomplete information.In this case, fuzzy language is considered to be the best tool to express fuzzy information.Therefore, there emerge a lot of sets to describe uncertain decision information.Such as fuzzy set, soft set, neutrosophic set (NS)[12], pathogenic hypersoft set [13], and their variants, etc.As a generalization of the intuitionistic fuzzy set, neutrosophic set [12] is used to describe uncertain, discontinuous and incomplete information.The main idea of NS is to describe every value statement in threedimensional neutrosophic space, where each dimension of the space represents respectively the truth-membership (T), the indeterminacy-membership (I)and the falsity-membership (F)of the statement under consideration, and T, I, F are standard or non-standard real subsets ofwhich do not necessarily have any connection between them.In order to apply NS theory to real life problems, some extensions of NS and some particular cases based on NS have been proposed.The existing fundamental extensions of NS contain single-valued neutrosophic set (SVNS)[14],interval neutrosophic set (INS)[15], multi-valued neutrosophic set (MVNS)[16], etc.MVNS is actually the Subset Neutrosophic Set, when all T, I, F are subsets of [0, 1] given by its founder Smrandache in 1998.Wang et al.[16] gave a precise definition of MVNS and multi-valued neutrosophic number (MVNN), and defined the Hamming distance and expected value of MVNN.

The second core part of MADM is integrating decision information and the ranking or selection of alternatives.At present, commonly used decision-making methods mainly contain TODIM (TOmada de Decisao Iterativa Multicriterio)[17], TOPSIS (The Order Performance technique based on Similarity to Ideal Solution)[18], VIKOR (VIsekriterijumska optimization I KOmpromisno Resenje)[19], EDAS (Evaluation Based on Distance from Average Solution)[20],PROMETHEE (Preference Ranking Organization METhod for Enrichment Evaluations)[21],MULTIMOORA (MULTIple Multi-Objective Optimization by Ratio Analysis)[22], and their variants, etc.Among them, TODIM method considers the psychological behavior of decision makers, which is closer to the actual situation.Besides, TOPSIS method is also an excellent MADM method for its simple and efficient calculation.Therefore, this paper mainly discusses the TODIM and TOPSIS methods.

As a most used MADM method, TODIM method takes psychological behavior of decision makers into consideration which is more in line with actual decision-making situations.Therefore,it has been developed rapidly and widely used since it was proposed by Gomes et al.[17].Fan et al.[23] solved the hybrid MADM problem by TODIM method, with the attribute values given in forms of crisp numbers, interval numbers and fuzzy numbers; Ömür et al.[24] combined the TODIM method and linguistic term set (LTS)for solving the supplier selection problem; Liu et al.[25] extended the TODIM method to multi-attribute group decision-making (MAGDM)with intuitionistic uncertain linguistic information; Wang et al.[26] used the TODIM method to solve the hybrid MADM problems with four different forms: crisp number, interval number, triangular fuzzy number and trapezoidal fuzzy number; Wang et al.[16] proposed the TODIM method with MVNS; Jiang et al.[27] proposed a TODIM method for MADM problem with incomplete evaluations in the form of crisp numbers; Qin et al.[5] used the TODIM method with type-2 fuzzy sets for green supplier selection and performed the comparative analysis with the TOPSIS method; Ji et al.[28] defined a projection-based TODIM method under multi-valued neutrosophic environments and applied it in personnel selection; Based on an improved TODIM method, Wang et al.[29] solved a MADM problem with interval grey number; Wang et al.[30] proposed the probability multi-valued linguistic neutrosophic set and used the TODIM method for solving the multi-criteria group decision-making (MCGDM)problems; Xu et al.[31] and Xu et al.[32]discussed the MADM problem with TODIM method under the single-valued neutrosophic and interval neutrosophic environment; Mao et al.[33] used TODIM for enterprise performance evaluation of strategic emerging industries under probabilistic linguistic term environment; In order to deal with linguistic hesitant fuzzy information in multi-criteria decision-making (MCDM)problems, Zhou et al.[34] applied TOPSIS, VIKOR, and TODIM methods; Considering the behavior of decision makers, Chen et al.[35] used the TODIM method to deal with uncertain linguistic MAGDM and compared this method with TOPSIS method.

TOPSIS method is also a popular MADM method for its efficient and straightforward calculation.Rıdvan et al.[36] extended the TOPSIS method to MCDM problem with single valued neutrosophic information; Ye [37] developed an extended TOPSIS method for a MAGDM problem based on the single-valued neutrosophic linguistic set (SVNLS); Tian et al.[38] combined INS and TOPSIS to establish two optimisation models for MCDM; Liu et al.[39] proposed a TOPSIS method for MAGDM with INN based on cloud model; Biswas et al.[40] proposed a TOPSIS method for MAGDM under single-valued neutrosophic environment; Liang et al.[1] presented an extended TOPSIS method combined with LNN in metallic mining projects investment; Liang et al.[4] introduced a linguistic neutrosophic MCGDM TOPSIS method to university human resource management; Chen et al.[6] handled a green supplier selection with TOPSIS method based on the OWA distance of the SVNLS; Liu et al.[41] proposed a neutrosophic hesitant fuzzy linguistic term set and combined the TOPSIS method to solve MCDM problem; Huang et al.[2] used the TOPSIS method to solve the investment problem under intuitionistic fuzzy environment; Giri et al.[42] used the TOPSIS method for solving the MADM in the form of interval trapezoidal neutrosophic number; Chai et al.[43] handled a MADM problem based on SVNS and TOPSIS method; Tan et al.[44] proposed a method based on intuitionistic (hesitant)fuzzy set (IHFS)and TOPSIS; Abdel-Basset et al.[9,10] combined bipolar neutrosophic numbers and TOPSIS for estimating the intelligent medical devices selection, and further proposed a novel TOPSIS method with type-2 neutrosophic numbers for developing supplier selection; Nguyen et al.[45] developed a new TOPSIS method based on the proposed intuitionistic (hesitant)fuzzy set theory; Pei et al.[46] introduced a fuzzy linguistic multiset TOPSIS method and applied it in linguistic decision-making problems; Elhassouny et al.[47] simplified the TOPSIS method and combined it with SVNS for decision-making.

Based on different methodologies, each MADM method has its advantages, disadvantages and scope of application.For this, with the increasing number of decision-making methods, more and more researchers begin to consider combining the existing methods to propose some improved methods.Some studies of combining TODIM or TOPSIS with other methods are proposed.Ji et al.[48] proposed a QUALIFLEX method with a TODIM-based concordance index for treatment selection; Yang et al.[49,50] obtained the weight by DEMATEL and then ranked the alternatives by TOPSIS method; Abdel-Basset et al.[7] built a framework of supplier selection problems, which employed ANP to calculate weights of selected criteria and used TOPSIS to rank alternatives; Tian et al.[3] combined the DEMATEL method and TODIM method to handle the market segment evaluation and selection under single-valued neutrosophic environment;Bai et al.[8] presented a method based on grey theory and TOPSIS for sustainable supplier selection; With the LTS, Liu et al.[51] presented a novel integrated FMEA model based on cloud model theory and TOPSIS method; Tang et al.[11] determined the positive/negative ideal solution(P/NIS)of urban sustainability through TOPSIS method, and then ranked alternatives by grey relational analysis.

1.1 Motivations for Paper

Based on the above analysis, this paper proposes a method by combining the TODIM and TOPSIS methods under the MVNS, considering the bounded rationality of decision makers.The main motivations behind this paper are as follows:

(1)TODIM method fully considers the decision makers’risk aversion attitude on the basis of prospect theory, and can reflect the decision makers’risk preference by adjusting the parameters, which is more in line with the actual decision-making requirements.However,any two alternatives need to be compared in TODIM method and also lead to high computational complexity.It is meaningful to find an improvement method that not only reflects the bounded rationality of decision makers, but also overcome its computational complexity.

(2)TOPSIS method sorts the alternatives according to their closeness to the ideal solution(PIS and NIS)rather than making a pairwise comparison of any two alternatives thereby reduces the number of comparisons between alternatives and makes the calculation simple.But it only considers the closeness between each alternatives and the PIS (NIS), and does not taking the decision makers’risk aversion attitude into account.Therefore, finding an improvement method based on TOPSIS method to reflect the bounded rationality of decision makers is significant.

(3)MVNS is a good tool to describe the incomplete, indeterminate and inconsistent information accurately.Therefore it is necessary to propose a hybrid method under MVNS environment that not only has concise calculation process and scientific results but considers the decision makers’risk attitude.

In summary, inspired from these two methods, this paper proposed a new method based on TOPSIS and TODIM methods under MVNS environment.This hybrid method not only has concise calculation like TOPSIS method but also takes the decision makers’aversion attitude into account, which makes it has good scientificity, accuracy and maneuverability.

1.2 Organization of Paper

The reminder of this paper unfolds as Tab.1.

Table 1: The organization of the rest of the paper

2 Preliminaries

For a better understanding the content of this paper, this section introduces some basic concepts of NSs and MVNSs and their related definitions.

2.1 Neutrosophic Sets(NSs)

2.2 Multi-Valued Neutrosophic Sets(MVNSs)

Definition 4.[16] LetXbe a space of points (objects), a MVNSAinXis characterized by

whereTA(x),IA(x)andFA(x)are the truth-membership function, indeterminacy-membership function and falsity-membership function ofArespectively, with the condition of

Especially,

(1)ifTA(x),IA(x),FA(x)all have only one value, then the MVNSs are reduced to SVNSs;

(2)ifTA(x),IA(x),FA(x)all are interval value, then the MVNSs are reduced to INSs;

(3)ifTA(x)=∅, then the MVNSs are reduced to double hesitant fuzzy sets (DHFSs);

(4)ifTA(x)=FA(x)=∅, then the MVNSs are reduced to hesitant fuzzy sets (HFSs).

For convenience, suppose thatTA(x)=TA,IA(x)=IA,FA(x)=FAandA=〈TA,IA,FA〉is a MVNN.

Definition 5.[16] The complement of a MVNSAis denoted byACand is defined as

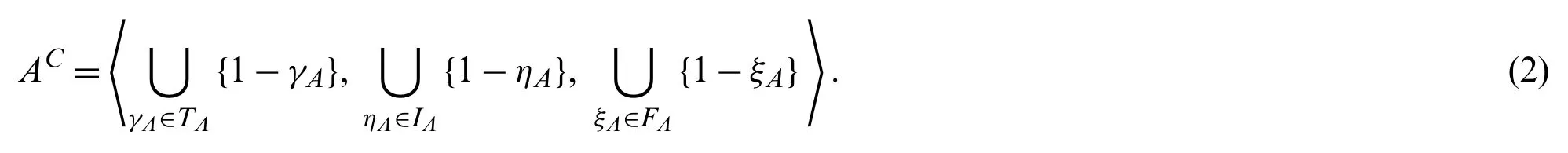
Example 1:LetA=〈{0.6},{0.1,0.2},{0.2}〉be a MVNS, the complement ofAis

AC=〈{0.4},{0.8,0.9},{0.8}〉.

Definition 6.[16] LetAbe a MVNS, so the expectation ofAis

where |TA|, |IA|, |FA|denotes the number of element inTA,IA,FA, respectively.

Example 2:LetA=〈{0.6},{0.1,0.2},{0.2}〉be a MVNS, so the expectation ofAis

Definition 7.[16] LetA=〈TA,IA,FA〉 andB=〈TB,IB,FB〉 be two MVNSs,A≺Bif and only if ∀γA∈TA,γB∈TB,ηA∈IA,ηB∈IB,ξA∈FA,ξB∈FBandγA<γB,ηA<ηB,ξA<ξB.

Example 3:LetA=〈{0.6},{0.1,0.2},{0.2}〉 andB=〈{0.7,0.8},{0.3},{0.5}〉 be two MVNSs.0.6<0.7, 0.6<0.8, 0.1<0.3, 0.2<0.3, 0.2<0.5, soA≺B.

Definition 8.[16] LetAandBbe two MVNNs, then the Hamming distance betweenAandBis

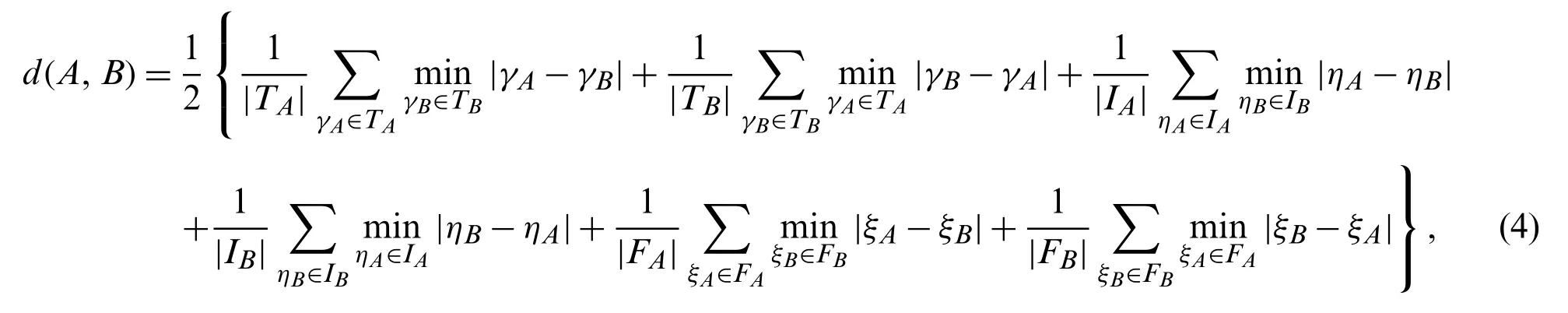
Example 4:LetA=〈{0.6},{0.1,0.2},{0.2}〉 andB=〈{0.7},{0.1,0.2},{0.1}〉 be two MVNSs,then the Hamming distance betweenAandBis

3 The Traditional Methods

3.1 The Traditional TODIM Method

The traditional TODIM method is a MADM method proposed by Gomes et al.[17] on the basis of the foreground theory in 1991.The main idea of this method is to establish the relative superiority function of one alternative over other alternatives based on the value function of the foreground theory.According to the obtained superiority, the ranking of alternatives is determined.The traditional TODIM method can only be used to deal with the fact that the attribute value is real.The main steps of TODIM method with MVNS in [16] are as follows:

Suppose that there aremalternativesA= {A1,A2,...,Am} andnattributesG={G1,G2,...,Gn}.Then the decision matrix can be denoted byA=(aij)m×nandaijbe an attribute value of the alternativeAiunder the attributeGj, wherei=1,2,...,m,j=1,2,...,n.The weights ofGjarewj, and 0 ≤wj≤1=1.The steps of the traditional TODIM method are as follows:

Step 1: Standardize the decision information.That is, normalizingA=(aij)m×nintoB=(bij)m×n.If the decision is a cost factor, the decision information should be changed by its complementary set, while an efficient factor, it should not be changed.

Step 2: Figure outwjr, which is the relative weight ofGjtoGr.Wherewr= max{wi|i=1,2,...,m},

Step 3: Figure out the dominance degree ofBiover every alternativeBtbyδ(Bi,Bt)=ϕj(Bi,Bt)(i=1,2,...,m), where

d(bij,btj)denotes the distance betweenbiandbtunderGj, andE(bij)is the expectation ofbij.This functionϕj(Bi,Bt)represents the dominance degree ofBiover every alternativeBtunder attributeGj, and the parameterθis the attenuation factor of the losses.IfE(bij)−E(btj)>0,ϕj(Bi,Bt)shows a gain, and ifE(bij)−E(btj)<0,ϕj(Bi,Bt)expresses a loss.

Step 4: Work out the overall dominance ofξiby following function:

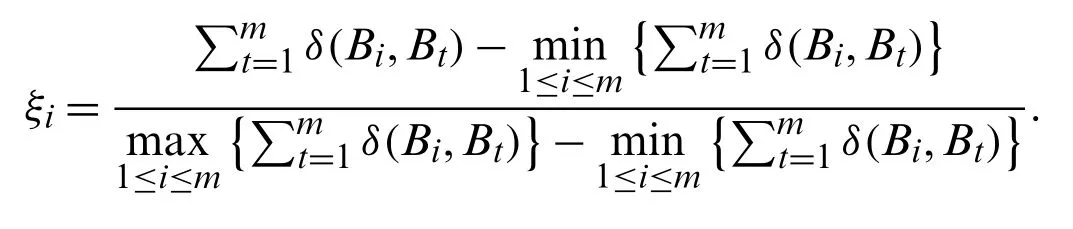
Step 5: Ranking all alternatives according to the value ofξi.The larger the value ofξi, the better the alternative is.

It can be seen that TODIM method fully considers the decision makers’risk aversion attitude on the basis of prospect theory, and can reflect the decision makers’risk preference by adjusting the parameters, thereby resulting in a more accurate decision-making process.However, decisionmaking information needs to be standardized firstly.Besides, any two alternatives also need to be compared in TODIM method in the case of more decision-making data, which leads to high computational complexity and large amount of calculation (such as distance and expectation values).

3.2 The Traditional TOPSIS Method

TOPSIS is a MADM method based on geometric thinking, which ranks candidate alternatives relatively far from ideal solutions and negative ideal solutions.On the basis of the TOPSIS method with IHFS in paper [44], we transformed it into a multi-valued neutrosophic environment and proposed a TOPSIS method with MVNS.The following shows the complete steps.

Let alternatives areA= {A1,A2,...,Am}, attributes areG= {G1,G2,...,Gn}, andaij(i=1,2,...,m,j=1,2,...,n)be an attribute value of the alternativeAiunder the attributeGj, andA=(aij)m×nbe an original decision matric.The weights ofGjarewj, andw=(w1,w2,...,wn),0 ≤wj≤1,=1.

Step 1: Get the decision matric and the corresponding weight.

Step 2: Figure out the weighted normalization matrix.

B=(bij)m×n=(aij·wj)m×n=(〈Tij,Iij,Fij〉)m×n.

Step 6: Ranking the alternative according to the value ofCi.The largerCiis, the better the alternative is.

TOPSIS method puts forward PIS (NIS)as reference point and only needs to compare each alternative with the ideal solution, which reduces the number of comparisons between alternatives when facing more decision-making data.So the calculation of TOPSIS method is simpler than TODIM method.However, from the formula of relative approximation coefficients, it can be seen that this method only uses distance measure to judge the quality of alternatives, and does not take the decision makers’risk aversion attitude into account, which lacks subjectivity.

4 The Proposed Method Based on TODIM and TOPSIS

When faced with a large amount of decision-making data, to consider the risk attitude of decision makers and simplify the calculation process, a hybrid MADM method based on TOPSIS and TODIM is proposed in this section.

Suppose in a MADM problem, there aremalternativesA={A1,A2,...,Am}andnattributesG={G1,G2,...,Gn}.Then the original decision matrix can denote byA=(aij)m×n, whereaij(i=1,2,...,m,j=1,2,...,n)is an attribute value of the alternativeAiunder the attributeGj.The weight ofGjarewj, andw=(w1,w2,...,wn), 0 ≤wj≤1,=1.Then, the MADM problem can be solved by the following steps:

Step 1.Obtain the decision matrixA=(aij)m×n=(〈Tij,Iij,Fij〉)m×n;

Step 5.According to the concept of value function and behavioral economics in prospect theory, if the PIS is taken as a reference point, then the alternatives will lose relative to the PIS;on the contrary, if the NIS is taken as a reference point, the alternatives will benefit.So the cost function is

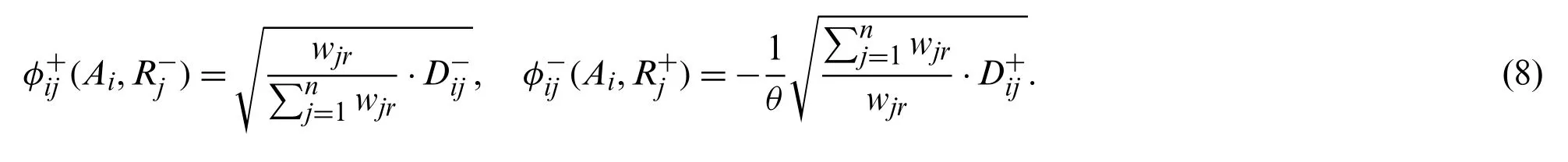
The parameterθis the attenuation factor of the losses, which can be adjusted according to the preference of the decision maker.Ifθ <1, the impact of loss will expand, and the impact will decrease whileθ>1.

Step 6.Figure out the overall valueψiand rank the alternatives byψi.The largerψiis, the better the alternative is.

It is obvious that the proposed method does not need to standardize the overall decisionmaking data according to attribute classification and it does not need to calculate the distance between any two alternatives and the expectation value of each alternative.In this sense, the proposed method is simpler than TODIM method in calculation.Besides, the proposed method is also based on TODIM method, taking the bounded rationality of decision makers into account,thus making up for the shortcoming of TOPSIS method.Therefore, facing to large number of alternatives, the proposed method can reduce the computational complexity and load more than TODIM or TOPSIS, which lead to a more simple decision-making process and a more reasonable result.

5 Application

In this section, two illustrate examples of the personnel selection problem and teaching evaluation problem adapted from Wang et al.[16] and Ye [52] are mentioned to demonstrate the validity and feasibility of the proposed methodology.

5.1 Case 1:Company Personnel Selection

Personnel selection is an important part of modern human resource management and also an important part of the company’s operation.It is directly related to the company’s output quality and efficiency.Good talents are the guarantee of good products.In the personnel selection process, the interviewer needs to evaluate candidates based on their performance in various aspects,which can be regarded as an MADM process.Thinking about the ambiguity and complexity of people’s thinking and language, MVMS can be used to express the evaluation information of the interviewer.

Suppose that a food company wants to hire a product manager.After preliminary screening of dozens of resumes, there are four candidates in the talent market that meet the recruitment requirements, which are denoted byA={A1,A2,A3,A4}.The interviewer needs to interviews the four candidates and evaluates them based on three attributes denoted byG1: working experience,G2: communication skill, andG3: frequency of job hopping.The evaluations of the four candidates under each criterion are transformed into MVNS, and the weights of attributes are given by the interviewer asw=(0.20,0.25,0.55).Then, the MADM problem can be solved by the proposed method involving the following steps:

Step 1.Obtain the decision matrixA=(aij)m×n=(〈Tij,Iij,Fij〉)m×n

The original decision matrix is obtained as shown in Tab.2.

Table 2: The original decision matrix of Case 1

Step 2.Determine the PISand the NIS

According to the attributes characteristics,G1andG2are efficient factors andG3is cost factor, so the PISand NIScan be calculated as shown in Tab.3.

Table 3: and of Case 1

Table 3: and of Case 1

?

Step 3.Calculate the distanceandrespectively;

According to Eq.(4), the distancebetweenAiandare calculated as

Step 4.Figure outwij, which is the relative weight ofGjtoGr.

According to Eq.(7), the relative weights ofGjtoGrare shown in Tab.4.

Table 4: wj and wjr of Case 1

Step 5.Calculate the dominance degree matrices.

Let the parameterθ=1, and the dominance degree matrices can be obtained as

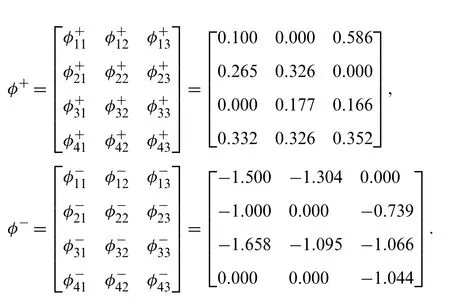
Step 6.Figure out the overall valueψiand rank the alternatives byψi.

Finally, the overall dominances are shown in Tab.5.It is obvious thatA4is the best choice andA2is the suboptimal one, however,A3is the worst option.

Table 5: The overall dominances and the final result of Case 1

5.2 Case 2:University Teaching Evaluation

Teaching evaluation is an important means for education administrative departments to supervise the teaching quality of colleges and universities.The purpose is to improve the quality of education and teaching.It is not only an important part of the teaching process but the basis of effective teaching and successful teaching.Specifically, according to certain teaching goals and standards, such as teaching completion, teaching concepts, teaching quality, etc., it systematically detects teachers’ teaching and evaluates its value, advantages and disadvantages, in order to improve.This can also be regarded as a MADM problem.Due to the complexity of the reality,its attribute values are often not directly represented by crisp set.In this condition, MVNS has become a good tool for expressing attribute values.

Assume that an education administration department in a certain place wants to evaluate the teaching of four local universities which are denoted byB={B1,B2,B3,B4}.The department need to evaluates the four universities according to three attributes denoted byC1: teaching accident,C2: teaching quality, andC3: teaching philosophy under MVNS environment.The weights of attributes are given by the department asw=(0.35,0.25,0.40).Then, the MADM problem can be solved by the following steps:

Step 1.Obtain the decision matrixB=(Bij)m×n=(〈Tij,Iij,Fij〉)m×n

The original decision matrix is obtained as shown in Tab.6.

Table 6: The original decision matrix of Case 2

Step 2.Determine the PISand the NIS

According to the description,C1is cost factor, whileC2andC3are efficient factors, so the PISand NIScan be calculated as shown in Tab.7.

Table 7: and of Case 2

Table 7: and of Case 2

C1 C2 C3 R+ 〈{0.3,0.4,0.5},{0.1},{0.3,0,4}〉 〈{0.6,0.7},{0.1},{0.2}〉 〈{0.6,0.7},{0.1,0.2},{0.1,0.2}〉R− 〈{0.7,0.8},{0.1},{0.1,0.2}〉 〈{0.5,0.6},{0.2,0.3},{0.3,0.4}〉 〈{0.2,0.3},{0.1,0,2},{0.5,0,6}〉

Step 3.Calculate the distanceandrespectively;

Step 4.Figure outwij, which is the relative weight ofCjtoCr.

Next, according to Eq.(7), the relative weights ofCjtoCrare shown in Tab.8.

Table 8: wj and wjr of Case 2

Step 5.Calculate the dominance degree matrices.

Assume the parameterθ=1, then the dominance degree matrices can be obtained as

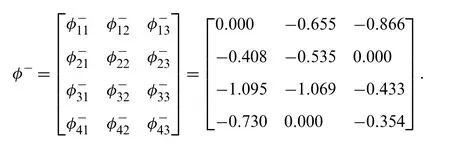
Step 6.Figure out the overall valueψiand rank the alternatives byψi.

Finally, the overall dominances are shown in Tab.9.The final result explains thatB2is the best choice andB4is the suboptimal one, however,B3is the worst option.

Table 9: The overall dominances and the final result of Case 2

6 Comparison and Analysis

6.1 Sensitivity Analysis

Since the proposed method is based on TODIM method, the parameterθcan reflect the risk preference of decision maker.Thus, in this subsection, the influence of the parameterθin the illustrate examples narrated in Section 5 are discussed in details.

As mentioned in Section 4, parameterθis the attenuation factor of the losses.According to Eq.(8), we can see that ifθ <1, the impact of loss will be amplified and the degree of amplification increases as the value ofθdecreases.On the contrary, ifθ >1, the impact will decrease.In order to study the influence of parameterθon the decision results, we changed the parameterθin Case 1 and Case 2, and observed the changes in the results.The details are as follows:

Case 1:Let parameterθvaries from 0.01 to 15.00, the results are shown in Tab.10.From it we can see that, the final ranking changes slightly with the value ofθ.When 0.01 ≤θ≤11.12,the final ranking remains asA4≻A2≻A1≻A3, and when 11.13 ≤θ≤15.00, the final result has changed toA4≻A1≻A2≻A3.But the optimal choice remains inA4.That’s because when 0.01 ≤θ≤1.00, the value ofθis at a low level.And in this condition, the impact of loss will expand and the decision makers are prone to choose the alternative with the least loss as the optimal choice.With the increase ofθ, the risk attitude of the decision maker gradually changes.Whenθ>1, the losses are attenuated.And whenθ>11.12, the degree of loss attenuated is large enough to change the decision maker’s ranking ofA1andA3.But theA4is dominant enough that no matter howθchanges in the range of 0.01–15.00, it is still the best choice.This can also be seen from the decision matrix in Tab.2.

Case 2:Tab.11 shows the results of case 2 when parameterθvaries from 0.01 to 5.00.From it we can see that the final ranking also changes with the value ofθ.When 0.01 ≤θ≤2.44, the final ranking areB2≻B4≻B1≻B3, and when 2.45 ≤θ≤5.00, the final result has changed toB2≻B4≻B3≻B1.But the optimal choice is alwaysB4.When 0.01 ≤θ≤1.00 the value ofθis at a low level and the losses are amplified.In this condition,B3is the most unwilling option for decision makers andB1is superior toB3, but inferior toB4andB2.This ranking continues untilθincreases to 2.45.Whenθreached to 2.45, the dominance ofB1andB3has been exchanged.And in this time, the decision makers are more unwilling to chooseB1rather thanB3.Besides,B2is always the optimal option andB4is the suboptimal one no matter howθchanges from 0.01 to 5.00.

Table 10: Changes of θ in Case 1

Table 11: Changes of θ in Case 2

In summary, when the parameterθchanges in Case 1 and Case 2, the final ranking will also changes, which implies that the parameter can really reflect the risk preference of decision maker.Thus, the decision makers can adjustθin decision making process to make more accurate and reasonable result.

6.2 Comparative Analysis

In order to verify the effectiveness, feasibility and superiority of the proposed methodology,we compared the results of the two cases applied in Section 5 with some existing methods.Details are as follows:

Case 1:In recent years, there have been several MADM methods to solve the MVNS environment such as TODIM method proposed by Wang et al.[16], whose are also the proposer of MVNS, MVNWBM operator and MVNWGBM operator [53], etc.Besides, MVNS was also called single-valued neutrosophic hesitant fuzzy set (SVNHFS)by Ye [52].There are also some methods to solve single-valued neutrosophic hesitant fuzzy set MADM problem.So we compared the results of Case 1 with five existing methods.To be specific, the comparative study was based on the same illustrative example in which the weights of attributes arew=(0.20,0.25,0.55).Then, the results by utilizing different approaches with complete weight information are shown in Tab.12.

As shown in Tab.12, it can be seen that, the ranking result of the proposed method whenθ=1 is the same as TODIM method and MVNWGBM operator, while slightly different from the TOPSIS, VIKOR and MVNWBM operator.The reasons are as follows: (1)the five methods are based on different ideologies, and it is reasonable that different procedures lead to different results;(2)the proposed method is based on TODIM method but simplified its calculation process, so the ranking result is the same as TODIM; (3)compared with TOPSIS method, the proposed method takes the decision makers bounded rationality into account, so the result is slightly different from the former.Despite this, the optimal choices and the worst option in five methods are the same,which proves the feasibility of the proposed method to a certain extent.

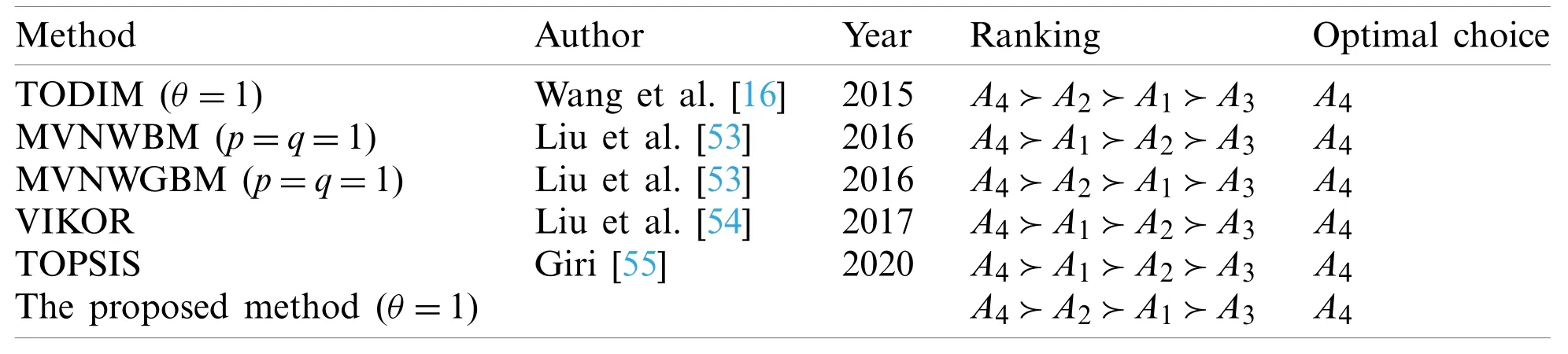
Table 12: Compared results utilizing the different methods with Case 1

Case 2:There are many approaches to deal with MCDM in SVNHFS environment, such as the approaches based on Weight operators [52], Hamming distance [56], Correlation coefficient [57], Choquet aggregation Operators [58], and so on.They can also be used in MVNS environment.Therefore, as in Case 1, these approaches are used to deal with Case 2 and compared with the proposed method.For the convenience of comparison, the weights are all setw=(0.25,0.35,0.40), and the results are shown in Tab.13.

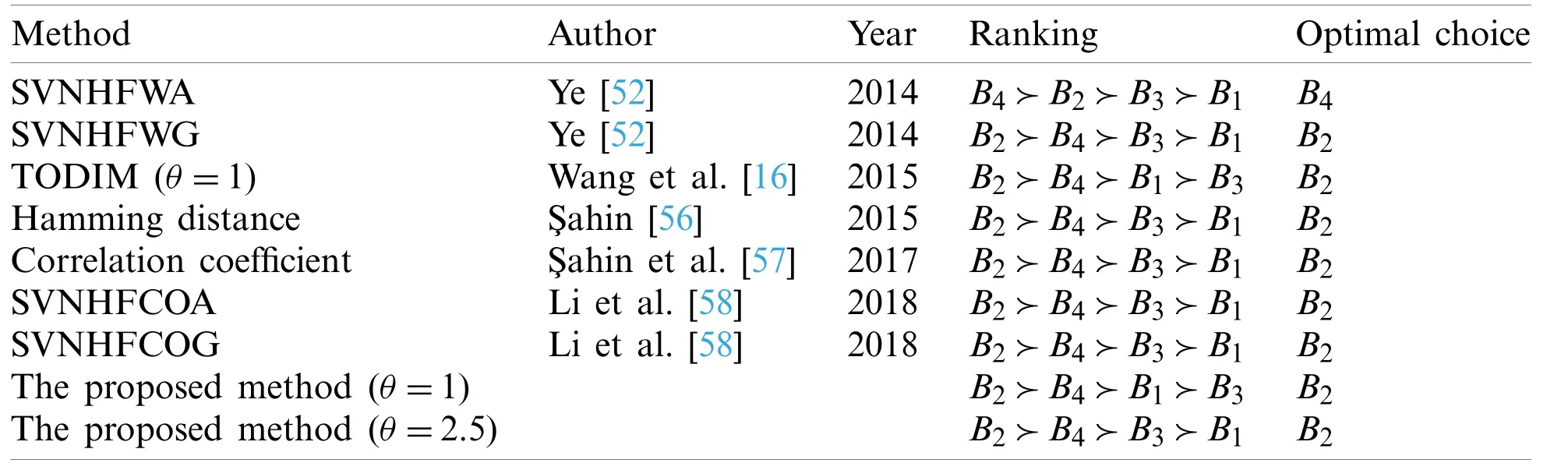
Table 13: Compared results utilizing the different methods with Case 2

From Tab.13, we can see that the final results of the several methods are slightly different.The ranking obtained by SVNHFWA operator is different from others, and the optimal choice isB4while other approaches areB2.This is caused by different concepts of different methods.Nevertheless,B2andB4are still better thanB1andB3.In addition to the first method, the optimal choice for the other approaches are alwaysB2, and the suboptimal one isB4, but the other two alternatives are sorted slightly differently.When the loss attenuation coefficientθ=1,the proposed method and the TODIM method proposed by Wang et al.[16] have the same result.And whenθ=2.5, the result of the proposed method is same as the others five methods.The reasons are as follows: (1)different ideas of different methods lead to different ranking results;(2)B2andB4are obviously superior toB1andB3, which can also be seen from Tab.6 of the original decision matrix.Therefore, all methods satisfy this point; (3)the proposed method can reflect the risk preference of decision makers by adjusting the loss attenuation coefficientθ, so differentθmay correspond to different results.These results prove the feasibility and effectiveness of the proposed method.

In summary, among the above methods, only the proposed method and TODIM method take the decision makers bounded rationality into account, which can make the result more accurate.But when the alternatives or attributes increase, the calculation amount of the proposed method is much smaller than that of the traditional TODIM method.In this sense, the proposed method is superior to the TODIM method.Thus, the advantages of the proposed method are as follows:

(1)Based on the TODIM method, it considers the bounded rationality of decision makers and reflect the risk preference of decision makers by adjusting the loss attenuation coefficientθ.

(2)The proposed method does not need to standardize the original matrix according to different attributes, which simplifies the calculation process to a certain extent.

(3)The proposed method uses PIS and NIS in the TOPSIS method as reference points, and uses the distance between the alternatives and the reference point to replace the pairwise comparison between alternatives, which makes the calculation simple.When faced with a large amount of decision-making data, the proposed method can use relatively simple calculations to obtain more reasonable result.

7 Conclusion

As a subset of neutrosophic set, MVNS is an excellent tool to describe uncertainty, incomplete and imprecise information.The elements in the truth-membership, the indeterminacy-membership and the falsity-membership in MVNS are extended to finite sets of discrete values, which enriched the expression of fuzzy information on the basis of fuzzy languages such as SVNS and INS.Therefore, based on the traditional TODIM and TOPSIS methods and the related research achievements of MVNS, this paper proposed a new method to handle the MCDM problems under MVNS environment.First, the traditional TODIM and TOPSIS methods are reviewed.And then, the specific steps of the hybrid method are introduced.In the new method, the distance between the alternatives and the ideal solutions is calculated by standardized Hamming distance of MVNS.Subsequently, the proposed method is used to solve two MADM problems about company personnel selection and university teaching evaluation under MVNS environment.These two cases all illustrate the feasibility and applicability of the proposed method.Moreover, by adjusting the loss attenuation coefficientθin the two cases, the sensitivity of new method is analyzed, and the validity of the method is also proved.Finally, the results of those two cases are compared with some existing methods, and the effectiveness and superiority of the proposed method are verified.The main advantages of the proposed method over other methods are not only the embodiment of risk preference for decision makers, but also the reduction of its computation.It is more in line with actual situations in real decision-making problems, thereby makes the final result more accurate and credible.

There are several directions for future research.Firstly, in addition to personnel selection and teaching evaluation, the proposed method should be used in more fields, such as venture capital selection, medical diagnoses, supplier selection, and so on.In addition, the proposed method assumes that the weight of the attribute is given by the decision maker, and does not discuss the situation with unknown attribute weight.Therefore, in the future, we will devote ourselves to improving the method to cover this deficiency and applying it to natural and complex decision-making processes.

Acknowledgement:Thanks to the co-authors for their help in the research process, for providing language assistance, writing assistance and proofreading for this article.

Funding Statement:This research was funded by the Humanities and Social Sciences Foundation of Ministry of Education of the Peoples Republic of China (17YJA630115).The recipient of the founding is DX.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.