Fractional Analysis of Dynamical Novel COVID-19 by Semi-Analytical Technique

S.Iqbal,D.Baleanu,Javaid Ali,H.M.Younas and M.B.Riaz

1School of Systems and Technology,University of Management and Technology,Lahore,54770,Pakistan

2Department of Mathematics,Cankaya University,Ankara,06530,Turkey

3Institute of Space Sciences,Magurele,Bucharest,077125,Romania

4Department of Mathematics,Govt.College Township,Punjab Higher Education Department,Lahore,54770,Pakistan

5Department of Mathematics,Islamia University of Bahawalpur,Bahawalpur,63100,Pakistan

6Department of Mathematics,University of Management and Technology,Lahore,54770,Pakistan

7Institute for Groundwater Studies,University of the Free State,Bloemfontein,9300,South Africa

ABSTRACT This study employs a semi-analytical approach, called Optimal Homotopy Asymptotic Method (OHAM), to analyze a coronavirus(COVID-19)transmission model of fractional order.The proposed method employs Caputo’s fractional derivatives and Reimann-Liouville fractional integral sense to solve the underlying model.To the best of our knowledge,this work presents the first application of an optimal homotopy asymptotic scheme for better estimation of the future dynamics of the COVID-19 pandemic.Our proposed fractional-order scheme for the parameterized model is based on the available number of infected cases from January 21 to January 28,2020,in Wuhan City of China.For the considered real-time data,the basic reproduction number is R0 ≈2.48293 that is quite high.The proposed fractional-order scheme for solving the COVID-19 fractional-order model possesses some salient features like producing closed-form semi-analytical solutions,fast convergence and non-dependence on the discretization of the domain.Several graphical presentations have demonstrated the dynamical behaviors of subpopulations involved in the underlying fractional COVID-19 model.The successful application of the scheme presented in this work reveals new horizons of its application to several other fractional-order epidemiological models.

KEYWORDS Novel COVID-19; semi-analytical scheme; fractional analysis

1 Introduction

Humans have invented many scientific methods so far and have set in motion several steps to avoid, even to cure, some of the lethal diseases.Although they believed they had conquered nature,corona-virus appeared killing thousands of people in China.Coronavirus has also been spread in many countries from Africa to Europe.Coronavirus 2019 (COVID-19)is a contagious virus causing infection to the respiratory system and is widely spread from humans to humans.The first infected case of this new COVID-19 disease was identified on December 31, 2019 in the city of Wuhan, China, the capital of Hubei province [1].Reportedly, main symptom was development of the pneumonia without any diagnosable cause and the available therapies and vaccines were not found effective [2].It was also noticed that the transfer of the virus among human takes place due to their mutual contact [3].Following the spread of COVID-19 virus in Wuhan City of China,the virus was also spread to other Chinese cities rapidly.In turn, the virus was proliferated to other areas including Asia, Europe, and North America.It is known that it takes 2 to 10 days for signs to emerge.The symptoms include troubled breathing, fever and coughing.A total number of 4593 infected cases and 132 deaths were reported until January 28, 2020 and more details on the latest infections and deaths due to the virus were yet to come.

Mathematical models play a vital role not only in understanding the dynamics of infection but also in investigating the recommendable conditions under which the disease will persist or wiped out.Presently, governments and researchers have shown great concerns to COVID-19 because of high transmission rate and noteworthy disease induced death rate.The COVID-19 virus is generally transferred when an infected person releases droplets generated by sneezing, coughing or exhaling.The confirmed cases of COVID-19 have reached nearly fifty four million all around the globe, and more than 1.3 million deaths have been caused by this virus.As of November 13,2020, according to Worldometers [4] USA, Brazil and India are the top countries with maximum death tolls amounting to 2.48, 1.64 and 1.28 million, respectively.

Keenly tracking the corona virus transmission, researchers have organized to speed up the diagnostic processes, and several types of vaccines are under investigation against COVID-19.For example, Cao et al.[5,6] studied and discussed the outcomes features of victims of COVID-19 in ICUs.Nesteruk [7] proposed a susceptible-infected-recovered (SIR)epidemic model and extracted some valuable guidelines through statistical analysis of the model parameters.An amended SIR model of COVID-19 was proposed in another study [8] to predict the exact count of infections and the additional burden on ICUs and isolation units.The count of coronavirus cases appeared higher than the number of cases predicted by February 2020.It lead to exert more emphasize on focusing the research on modernizing the corona virus predictions in the view of latest data and considering more complex mathematical models.Presently, no patent therapeutic agents or vaccines for treatment or prevention from coronavirus are available, however the research based investigations into vaccine candidates and potential antivirals are ongoing in several countries.Drug development is a comparatively shorter process as compared to development, testing and distribution of vaccine and any cure for COVID-19 is not expected to be available before 2021.The dense places are ideal environments where the virus can spread easily.It was agreed that human close contact is one of the possible causes of COVID-19 outbreaks.Therefore, the quarantine of the COVID-19 victims can lessen the threat of further disease proliferation.The important measures taken to reduce the spread of virus include small contact rate and social distancing.The impact of such measures was investigated by Zeb et al.[9] by proposing and analyzing a SEIIR (susceptible-exposed-infected-isolated-recovered)model.They concluded that the individuals infected from coronavirus infectious disease must be referred to isolated compartment at various rates.A logistic growth model of COVID-19 was studied by Batista [10] and was employed to predict the ultimate volume of the epidemic.The dynamical behavior of coronavirus has been studied by several researchers through various COVID-19 transmission models [7–11].

Over the last thirty years, fractional derivatives have captivated the numerous researchers after recognition of the fact that in comparison to the classical derivatives, fractional derivatives are more reliable operators to model the real world physical phenomenons.In dynamical problems,fractional calculus (FC)based modeling is receiving a rapid popularity nowadays.The mathematical modeling of many physical and engineering models based on the idea of FC exhibits highly precise and accurate experimental results as compared to the models based on conventional calculus.The non-integer differential operators such as Caputo, Caputo-Fabrizio and ABC are fractional operators that transform the ordinary model to generalized model.In this article, we present a novel research on a fractional order dynamical model that underpins the propagation of coronavirus infectious disease and provide some forecasting with real world data.We extend an integer-order model formulation to a fractional order model by adding the Caputo sense of fractional derivative.The reason of using the Caputo fractional derivative is that it possesses several basic characteristics of fractional calculus.Moreover, the transmission behavior described in the model can be better defined by using Caputo operator.Research based on derivatives in Caputo sense and its applications to different models emerging in various disciplines of engineering and other sciences can be observed in several past studies [12–16].Few additional linked researches on Caputo and other fractional order derivative implementations can be found in literature [17–32].Since the number of infected cases reported from January 21 to January 28,2020 is comparatively higher than those of on initial days, therefore we have considered this period for the formulation of the mathematical model as a parameterized model.In Section 2,transitory details of various mathematical models showing evolution of COVID-19 from bats to humans have been provided.Section 3 presents basic properties of the fractional order COVID-19 model.The Section 4 consists of the development of a semi-analytical scheme for the solution of the considered fractional order COVID-19 model.The simulation results of the proposed scheme based upon model fitted data are presented in Section 5.In the end, some fruitful conclusions have been presented.

2 Mathematical Modeling of COVID-19 Evolution

Presuming that the transmission occurs primarily within the population of bats and afterwards the transmission occurs to wild animals usually termed as hosts.Hunting of these carriers and then their transportation to the supply markets of seafood are considered as virus reservoirs.By exposing to the market, people get the risk of infection.In the following subsections, we revisit the evolution of the COVID-19 evolutionary tracks from bats to humans in the form of three mathematical models.

2.1 Model 1:Transmission of Corona Virus-19 among Bats and Hosts Populations

From the mathematical modeling point of view, let us denote the size of entire population of bats byNband further classify it as four subclasses, namely, the subpopulation of susceptible bats denoted bySb, the subpopulation of exposed bats denoted byEb, the subpopulation of bats infected by the virus symbolized asIband the subpopulation of removed/recovered bats denoted byRb.The size of unknown host population is denoted byNhand is further categorized into four subgroupsSh;Eh;IhandRh, respectively representing the susceptible subpopulation,exposed subpopulation, infected subpopulation and the recovered or removed subpopulation of hosts.Therefore,Nb=Sb+Eb+Ib+RbandNh=Sh+Eh+Ih+Rh.

The susceptible bat population is hired via birth rateΠbwhere death rate isμbfor all types of bats.The exposed bats get infected at ratesθbafter having completed their incubation period and therefore, get included in the infected subpopulationIb.The rate of removal or recovery of infected subpopulation of bats is denoted byτbat which the subclassRbis populated.The infection due to the contact of infected population with the susceptible population takes place at a rateηband is denoted by the routeηb SbIb/Nb.We denote the birth rate of unknown hosts byΠhand the natural mortality rate byIh.The exposed members of host subpopulation get infection at a rateθhand enter into the infected subpopulation (Ih), whereasτhdenotes the infected host’s rate of removal/recovery.The pathηbh Sh Ib/Nhion subpopulationIh, models the interactions taking place among the infected bats and susceptible hosts, with the assumption thatηbhis the transmission coefficient of disease towards healthy hosts from infected population of bats.As a result of infection caused by infected members of bats population, the virus is potentially capable of dispersing inside the host’s population and is mathematically represented by the termηh Sh Ih/Nh, whereηhdenotes the disease transmission coefficient between the subgroupsShandIhof the host population.

Eqs.(1)–(8)are subject to some non-negative initial conditions.

2.2 Model 2:Transmission of COVID-19 from Seafood Market to Human

LetNp(t)denote the total population of individuals, which is again categorized into five subgroups such asSp(t);Ep(t);Ip(t);Ap(t)andRp(t)respectively representing the susceptible subpopulation, exposed subpopulation, infected (symptomatic)subpopulation, asymptomatically infected subpopulation, and the recovered or removed subpopulations of human.Simply, the following system of coupled system of nonlinear differential equations defines the evolutionary track of COVID-19 from hosts to human via seafood market reservoir.

The governing Eqs.(9)–(14)are also subject to some initial conditions.The parameterτaprepresents the removal or recovery rate ofAp,ηωis the coefficient of transmission of disease fromMtoSpandθpis the asymptomatic infection factor.

2.3 Model 3:Transmission of COVID-19 among Human with Reservoir

This model presents changing aspects of transmission of COVID-19 among human that are due to the close contacts of human population with the contagious environment without direct contact to virus hosts.Peoples’birth and natural death rates are denoted by the parametersρpandIp, respectively.The prone peopleSpwill be infected by ample encounters with the infected peopleIpthrough the definition provided byηpSpIpwhere theηpis coefficient of disease transmission.Transmission amongst asymptomatically infected healthy individuals may occur in the form ofΨ ηpSpAp, whereΨnumerous transmissibility ofApto theIpsuch thatΨ∈[0,1]; ifΨ= 0,there will be no numerous transmissibility, and ifΨ=1, the same will occur asIpinfection.Theθpvalue is the asymptomatic infection factor.Theωpandρpparameters respectively reflect the rate of transmission after the completion of the time of incubation and becoming infected,entering the classesIpandAp.The individuals in symptomatic classIpand asymptomatic classApjoin the groupRpwith the rate of removal or recovery byτpandτap, respectively.SectionMis the reservoir or the marketplace location where the seafood is stored.The prone individuals are affected byηωMSpafter contact withM, whereηωis the coefficient of transmission of disease fromMtoSp.The number of hosts who visit the seafood market for buying products(retail purchase)is indicated byband the corresponding infection is modeled through the relationbMIh/Nh.In view of the fact that the COVID-19 can be introduced into the seafood market in a short time with ample source of infection and hence, without lack of generality, the effect of disease transmission due to bats’contact to hosts can be ignored.Consequently, the following model is achieved:

There also exist some initial conditions of this model.Considering that the rates of symptomatic and asymptomatic infections due to reservoirMare constant, we denote these constant rates by parametersQpandϖp, respectively.The parameterπin Eq.(20)denotes the rate at which the virus is removal from environment reservoir as a result of some treatment policies implemented by policy makers.

3 Dynamical Fractional Order Model of COVID-19

To develop fractional order COVID-19 model, we describe some basic definitions from fractional calculus, which play vital role in fractional calculus for solving fractional order system of differential equations.These definitions consist of fractional integral operator of a functionf(t)in Riemann–Liouville sense and the fractional derivative of a functionf(t)in Caputo sense.

The integral operator of fractional order in Riemann–Liouville sense with orderα≥0 off(t)∈Cμis defined as beneath.

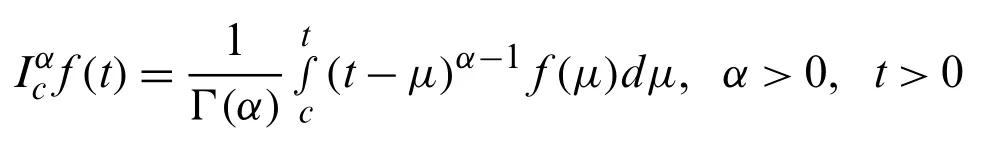
whereCμis said to be space andμ∈R,μ≥−1.The following formula describes Caputo sense based fractional order derivative operator.

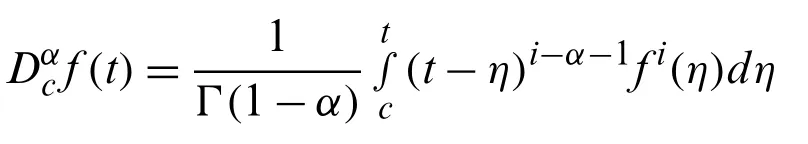
For i−1 ≤α≤i,i∈N,f(t)∈

Replacing the time derivatives of state variables by Caputo sense fractional order derivatives in Model 3, we obtain the following generalized COVID-19 model of fractional order in Caputo sense fractional derivative operator.

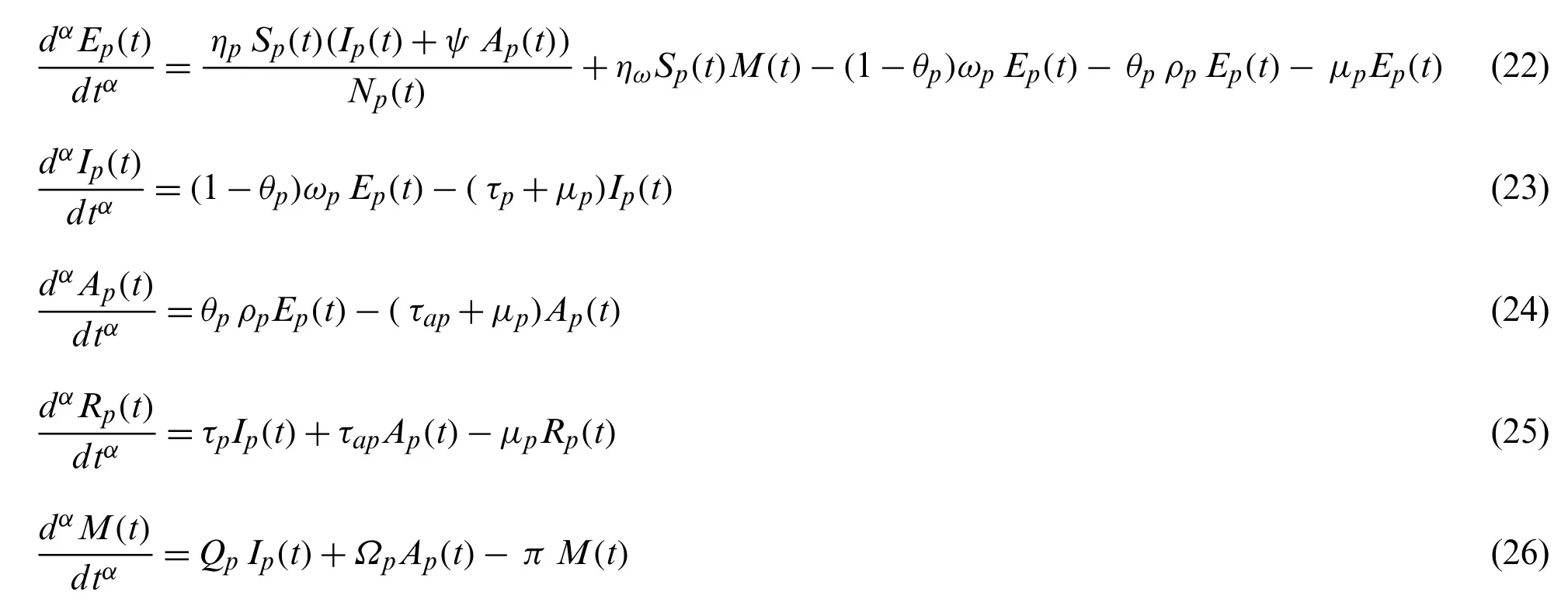
Initial conditions obeyed by the model are:

By adding Eqs.(15)–(19), we obtain human population’s total dynamics as under.

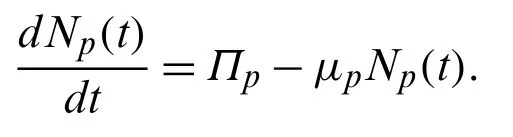
Integrating over [0,t] we get:

It implies that the total population has an upper bound ofat any time step.The positivity of the state variables and the upper bound of the entire population constitute the following feasible region for the model.

The points of equilibrium of the above fractional order dynamical COVID-19 model are calculated by solving the nonlinear algebraic equations obtained by equating the fractional time derivatives in Eqs.(21)–(26)to zero.Disease free and endemic equilibrium points denoted byD0andD∗respectively are given below:

The solution of the polynomial equationP(λ∗)=m1(λ∗)2+m2λ∗=0 is given as:

where,m1=π(μp+τp)(μp+τap)(θp(ρp−ωp)+μp+ωp),

m2=πμp(μp+τp)(μp+τap)(θp(ρp−ωp)+μp+ωp)(1 −R0).

Clearlym1>0 andm2≥0 wheneverR0<1, so thatλ∗=−m2/m1≤0, thus, no endemic equilibrium exists wheneverR0<1.

The essential reproduction quantity (R0)is usually defined as the number of supplementary infections that a certain infectious person would create on the period of the infectious time period provided that everybody else is susceptible.To compute the essential reproductive number (R0)of the Model 4, we follow the work in [33].

The spectral radiusγ(AB−1)gives the basic reproduction number of the Model 4.

The threshold value forR0is 1.IfR0<1, the size of secondary infections in human population will not be large enough for persistence of disease and hence the infection will die out over course of time.In the case whenR0>1, there will be a geometric increase in size of infected population and therefore the infection will continue to spread.The fitted values of transmission rates are presented in Tab.1.

Table 1: Values of the model parameters

4 Optimal Homotopy Asymptotic Method(OHAM)Scheme for Fractional COVID-19 Model

Now we develop OHAM scheme for solving underlying fractional order COVID-19 model.OHAM technique is known for its rapid convergence as compared to other techniques.It produces an approximate closed form of the desired solutions and, hence, is known as semi-analytical approach.Procedure of our approximate OHAM scheme has been derived by following the relevant principles as described in literature [34,35].The underlying COVID-19 fractional order model consists of six governing equations.In the following steps we carry out complete calculations of OHAM scheme for all equations of the model.

Step-1)Homotopies of the governing equations:

We construct the homotopy equations by defining the real valued functionsΦS(t,q),ΦE(t,q),ΦI(t,q),ΦA(t,q),ΦR(t,q)andΦM(t,q)on the domainΩ×[0,1] representing the approximate solutions of state variablesSp,Ep,Ip,Ap,RpandM, respectively.

In the above relationsΩ=[0, ∞),t∈Ω,q∈[0,1] andH(q,c)is an auxiliary function that is always nonzero for allq∈(0,1], whereasH(0,c)is necessarily zero.Auxiliary function in the above relation is defined as under:

Step-2)The steps of OHAM scheme for finding the approximate solution have been carried out in details for the first governing Eq.(28)only.The procedure for the remaining Eqs.(29)–(33)is quite similar.We start by expandingΦs(t,q,Ci)as a Taylor’s series aboutq.

The convergence of above series depends upon auxiliary constantsCi,i=1,2,...

Forq=1 we have

Step-3)Comparing the coefficients of like powers of ‘q’after using the Eq.(35)in Eq.(28)we can obtain approximations of order from zero to onwards, if needed, as below:

And so on.

Step-4)Using Reimann-Liouville sense of integral on governing equation of susceptible population and using the initial conditionSp(0), one can obtain following series solution.

whereΓ(α)denotes the gamma function.We have the solution in the form:

By substituting the values from Eqs.(40)–(42)in Eq.(43), we obtain second order approximate result of Eq.(21)as:

Adopting the same procedure presented in Steps 1–4, we find the following approximate solutions for the state variablesEp(t),Ip(t),Ap(t),Rp(t)andM(t).

Step-5)In this step, the values of auxiliary constantsC1andC2, present in Eqs.(44)–(49),are found by using the method of least squares [33,36,37] by minimizing the total error function of all the governing equations.Letχ={Sp,Ep,Ip,Ap,Rp,M} be the set consisting of all state variables andkbe any member of this set.The corresponding residual of each governing equation is denoted by ℜk:k∈χand total error function is denoted byJkand is defined as under:

The minimization process of eachJkis explained in following subsections of results and discussions.

5 Results and Discussion

This section is dedicated for presentation of the closed form semi-analytical solutions for all of the state variables and demonstration of their dynamics through graphical exhibition of related simulation results.Model 4 has total six equations.That means COVID-19 fractional model is to analyzed by observing the behaviors of six subpopulationsSp,Ep,Ip,Ap,RpandMfor the various values ofα.

The considered values for model parameters are presented by Tab.1.All figures in the following cases describe the individual behavior of model subpopulations for various values ofα.The evolution time t is taken in days by setting a scale of 10 to 1 along horizontal axes.

5.1 Dynamics of Susceptible Human Population

For the fractional analysis of human susceptible population we calculate the auxiliary constants (C1,C2)which describe the order of the solution.We will find these auxiliary constants so that the series solution defined by Eq.(44)satisfies the related governing equation COVID-19 Model 4.The corresponding error function is:

where, the residual, of susceptible population, denoted by ℜSp, is defined as under:

Imposing the necessary conditions for minimum residual, we can findC1andC2, by solving the equations:

Tab.2 presents the optimized values of auxiliary constants of the second order approximate solution for susceptible population considering various orders of fractional derivative.The corresponding second order approximate solution forSphas been exhibited in Tab.3.Fig.1 demonstrates a clear impact of varying values of the order of the fractional derivative on the dynamics of the susceptible population.

Table 2: The optimum values of C1 and C2 for Sp with varying α

Table 3: Second order approximate results for Sp with variousα

5.2 Dynamics of Exposed Population

The auxiliary constants (C1,C2)describing the order of the solution for exposed population have been calculated first by enforcing the series solution given by Eq.(45)to satisfy the second governing equation of the fractional order COVID-19 model.The total error function is given as:

where, the residual of exposed population, denoted by ℜEp, is defined as under:

Imposing the necessary conditions for minimum residual, we can findC1andC2by solving the equations:

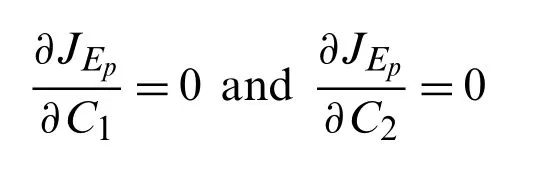
Considering various orders of the fractional derivative, above necessary conditions provide the relevant optimum values of auxiliary constants for the exposed population and are presented in Tab.4.

Figure 1: Susceptible population vs. time t

Table 4: The optimum values of C1 and C2 for Ep with varying α

The OHAM scheme based second order solution for the exposed populationEphas been shown in Tab.5 for various values ofα.Fig.2 describes the evolution of exposed population with respect to time.

Table 5: Second order approximate results for Ep with various α

Figure 2: Exposed population vs. time t

5.3 Dynamics of Infected(Symptomatic)Population

The values of auxiliary constantC1andC2, present in Eq.(46), have been calculated by minimizing the total residual functional given by:

where, the residual of infected (symptomatic)population, denoted by ℜIp, is defined as under:

Solving the following equations forC1andC2we get their optimum values that are presented in Tab.6 for various values ofα.The corresponding OHAM scheme based second order approximate solution for infected population is shown in Tab.7.The graphical view of evolution of infected population under the influence of various values of order of the fractional derivative has been exhibited in Fig.3.

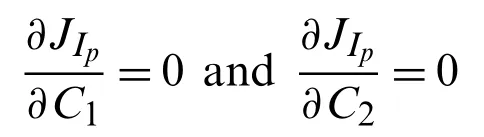
Table 6: The optimum values of C1 and C2 for Ip with varying α

Table 7: Second order approximate results for Ip with various α

Figure 3: Infected population vs. time t

5.4 Dynamics of Asymptotically Infected Population

The values of auxiliary constantC1andC2involved in Eq.(47)of asymptotically infected population have been calculated as follows:

where, the residual of asymptotically infected population, denoted by ℜAp, is defined as under:

The values ofC1andC2presented in Tab.8 have been obtained by solving following equations:

Tab.9 displays the second order solution forAp.Fig.4 demonstrates the evolutionary behavior of asymptomatically infected population over time.

Table 8: The optimum values of C1 and C2 for Ap with varying α

Table 9: Second order approximate results for Ap with various α

Figure 4: Asymptomatically infected population vs. time t

5.5 Dynamics of the Recovered or the Removed Population

The following total error function corresponding to recovered population is obtained from Eq.(48):

The residual ℜRp, for the recovered or the removed population, is defined given as:

Solving the following necessary conditions we obtain the values ofC1andC2presented in Tab.10.

The closed form solution for recovered population is presented in Tab.11 using different values ofαand the relevant graphs are exhibited in Fig.5.

Table 10: The optimum values of auxiliary coefficients for with varying α

Table 11: Approximate solution for Rp with various values of α

Figure 5: Recovered population vs. time t

5.6 Dynamics of the Reservoir Compartment

Applying the least square approach for the auxiliary constant of Eq.(49)we get following total error function:

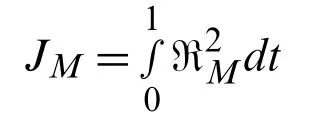
The residual ℜMof the classMis defined below:

The solutions of following equations give the values ofC1andC2shown in Tab.12:

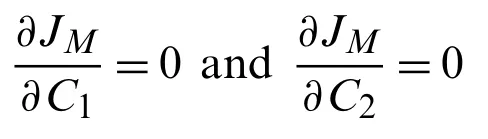
The approximate solutions forMhave been presented in Tab.13 whereas the impact of variation in order of the fractional derivative has been shown in Fig.6.

Table 12: Auxiliary coefficients for M with varying α

Table 13: Approximate solution for M with varying α

Figure 6: Reservoir saturation vs. time t

6 Conclusion

In this study, closed form semi-analytical approximate solution has been presented for fractional order COVID-19 model in Caputo sense of derivative operator.The underlying model involves parameters that were extracted by fitting real data into the dynamical model.The fitted parameters are responsible for a high reproduction numberR0≈2.48293 that indicates the fact that the infection will persist.The sensitivity ofR0reveals that the infection can be controlled by reducing the contact ratesηpandψof susceptible population to symptomatically and asymptomatically infections, the contribution ratesΩpandQpof infected populations to environment and the reservoir’s disease transmissibility rateηω.Such reductions can be directly achieved by implementing more quarantining, hospitalization and lockdown strategies by policymakers.Moreover, the availability of a healthy environment to increase population immunity and effective remedies will increase the recovery ratesτapandτawhich will result in a reduced reproductive number.Taking into account of available data and the fitted parameters, the dynamics of human subpopulations have been efficiently examined by considering various values of order of fraction derivatives.Analytical and graphical results demonstrate that an increase in the orderαof fractional derivative shows increase in the exposed, symptomatically infected, asymptomatically infected and recovered subpopulations sizes whereas the number of susceptible individuals and environmental saturation decrease.The results obtained are promising providing us great inspiration to use our proposed methodology further to explore more advanced models of COVID-19 disease, especially, delayed and stochastic models.It is expected that this latitude study would provide researchers a good viewpoint of more advanced research that could be put forward on closed form solutions of epidemiological models.

Acknowledgement:The authors are thankful to their respective departments and Universities.

Funding Statement:The authors received no specific funding for this study.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.