Dynamical Analysis of Radiation and Heat Transfer on MHD Second Grade Fluid

Aziz-Ur-Rehman,Muhammad Bilal Riaz,2,Syed Tauseef Saeed and Shaowen Yao

1Department of Mathematics,University of Management and Technology,Lahore,54770,Pakistan

2Institute for Groundwater Studies(IGS),University of the Free State,Bloemfontein,9301,South Africa

3Department of Science&Humanities,National University of Computer and Emerging Sciences,Lahore,54000,Pakistan

4School of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo,454000,China

ABSTRACT Convective flow is a self-sustained flow with the effect of the temperature gradient.The density is non-uniform due to the variation of temperature.The effect of the magnetic flux plays a major role in convective flow.The process of heat transfer is accompanied by a mass transfer process;for instance,condensation,evaporation,and chemical process.Due to the applications of the heat and mass transfer combined effects in a different field,the main aim of this paper is to do a comprehensive analysis of heat and mass transfer of MHD unsteady second-grade fluid in the presence of ramped boundary conditions near a porous surface.The dynamical analysis of heat transfer is based on classical differentiation with no memory effects.The non-dimensional form of the governing equations of the model is developed.These are solved by the classical integral(Laplace)transform technique/method with the convolution theorem and closed-form solutions are attained for temperature,concentration,and velocity.The physical aspects of distinct parameters are discussed via graph to see the influence on the fluid concentration,velocity,and temperature.Our results suggest that the velocity profile decrease by increasing the Prandtl number.The existence of a Prandtl number may reflect the control of the thickness of momentum and enlargement of thermal conductivity.Furthermore,to validate our results,some results are recovered from the literature.

KEYWORDS Heat transfer; magnetic effect; ramped conditions; porous medium; Laplace transform; thermal radiation

1 Introduction

In the literature, different theories are made to see the phenomenon of heat transfer analysis.Radiation, convection, and conduction are three modes of heat transfer.Convection can be defined as heat transfer by the substance motion which may be air or water.It plays a central role in creating the weather clause on the plant.Convection consists of forced and natural convection.It happens when the medium divides the heat energy and is on its move.Heat is disbursed when a fan pushes air, and sometimes heat advection is referred to the forced convection.Heat is animated to distress by means of itself hotness becomes the cause of natural convection by means of shifting source heat.Heat and mass are related to each other as heat transfer rate depends on mass transfer and mass transfer further depends upon concentration difference.Free convective flow is a self-reliant flow with the effect of heat transfer.In different industrial problems, the fluid flow phenomenon of free convection has achieved much consideration in recent years.The atmospheric, oceanic circulation, and emergency cooling system of advanced nuclear reactors is the most important application of free convection.The effect of heat transfer in non-Newtonian fluids plays a major role applying engineering such as drag reduction, the emergency cooling system of nuclear reactors, and thermal welding.In literature, different theories are made to see the phenomenon of heat transfer analysis.The convection heat transform between two heated cubes was discussed by Mousazadeh et al.[1].Sajad et al.[2] investigated the heat transfer and magnetic effects on hybrid nanofluid.Iftikhar et al.[3] analyzed the influence of heat and mass transform with the existence of a magnetic field in the rate type fluid model.Convective flow is a self-reliant flow with the effect of the heat transfer.The influence of magnetic flux plays a significant role in convective flow.In the literature, different theories are made to see the phenomenon of heat transfer analysis.Radiation, convection and conduction are three modes of heat transfer.Convection can be defined as heat transfer by the substance motion which may be air or water.It plays a central role in creating the weather clause on the plant.

Qi et al.[4] investigated the mathematical analysis of the heat transfer model subject to the stretching plate with the velocity slip boundary for the Maxwell fluid model.They explored the exact solutions using the effect of the heat flux relaxation time, slip coefficient, and the Prandtl number.Literature shows more interest in developed identical studies in [5–8].Ramped heating plays a good role in real-life problems such as prognosis diagnoses, heart function analysis, and blood vessel system [9–11].Moreover, Kundu [12] investigated the thermal therapy based on ramped heating to destroy the cancer cells on the human structure.Researchers in [13–17] used the ramped heating to investigate the flows of Newtonian and non-Newtonian fluids.Initially,convective viscous fluid with ramped heating over vertical wall was analyzed by Schertz [18] and Hayday [19].The flow of a viscous fluid with the impact of ramped temperature over a moving surface was analyzed by Das et al.[20].The heat absorption ramped heating and thermal effect near a moving wall was discussed by Seth et al.[21].The time-dependent motion with a slip effect on ramped surface was investigated by Maiti et al.[22].Seth et al.[23,24] investigated the dynamical aspect of mass and heat transformation with Darcy’s law, chemical reaction, and thermal conditions.Previously, there was less study which deals the simultaneous use of ramped heating with ramped velocity.It is complicated to apply these conditions simultaneously, but they have broad significance as a physical aspect.Recently, Tiwana et al.[25] and Anwar et al.[26]analyzed the effect of ramped temperature and ramped velocity in the existence of thermal radiation.Anwar et al.[27] analyzed the impact of ramped wall temperature and ramped velocity on Maxwell fluid.Anwar et al.[28] investigated the exact solution of second-grade fluid under the impact of ramped conditions.The different technical problems, the flow of fluid in the existence of heat radiation has been achieved consideration in recent years.The power plant for rocket ignition,missile and emergency gas-cooling system are the most important application of heat radiation.The influence of heat radiation on micro-polar nanofluid with magnetic effect was discussed by Izadi et al.[29].The exact solution of magneto nanofluid with free convection and heat radiation effect was investigated by Das et al.[30].Two phase model for nanofluid was investigated by Sheikholeslami et al.[31] using impact of heat radiation.Gangadhar et al.[32] investigated the role of heat radiation and Newtonian heating on ferrofluid.The Numerical results for Casson fluid under the effect of heat radiation, and Newtonian & Joule heating was investigated by Seth et al.[33].

Although the research on the Second grade model can be continued, we include here some related studies based on heat transfer, fractional models of fluids, magnetized fluids, and few others therein [34–40].Motivating by above discussion, this manuscript aims to explore the unique and exact solution of MHD Second grade model with simultaneous use of ramped heating with ramped velocity near a porous surface.Laplace integral transformation is used to obtain the unique solution of velocity, temperature, and concentration under impact of ramped heating.In Section 2, the dimensionless governing equations are developed.In Section 3, Laplace integral transform is used to find the exact solution of the temperature, velocity, and concentration field.In Section 4, some existing results are recovered as the limiting cases to justify our results.In Section 5, the effect of physical parameters is analyzed graphically.The concluding observation is listed at the end.

2 Development of Governing Equations Based on Problem Statement

Consider the MHD Second grade fluid flow in a porous medium over an limitless vertical plate.Initially, the fluid is at rest att= 0.Aftert < t0, theis the plate temperature with velocityAtt>t0, it give constant velocityw0with temperatureT∞.The fluid flow is one dimensional.The flow direction of radiative flux is negligible.Finally in energy equation, the dispersion term is neglected.The geometrical presentation of considered model is provided in Fig.1.Under some these presumptions, the governing equation for MHD Second grade fluid with appropriate conditions are given below [28]:

with appropriate conditions

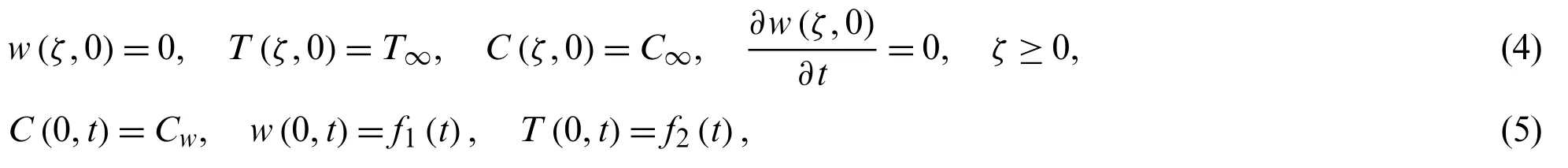
where

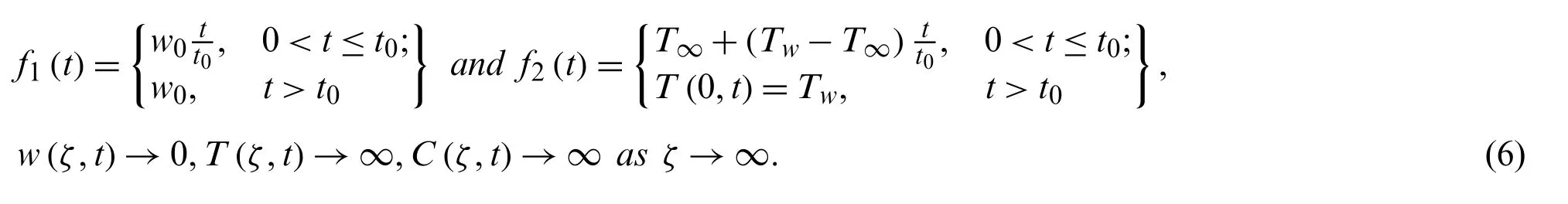
Consider the different dimensionless quantities

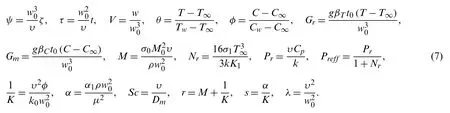
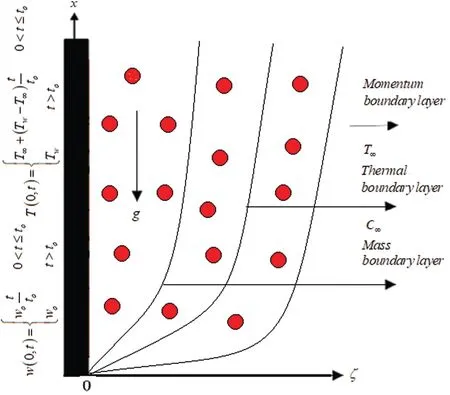
Figure 1: Geometrical presentation for second grade model

After simplification, we have the set of dimensionless governing equations and their corresponding conditions are:

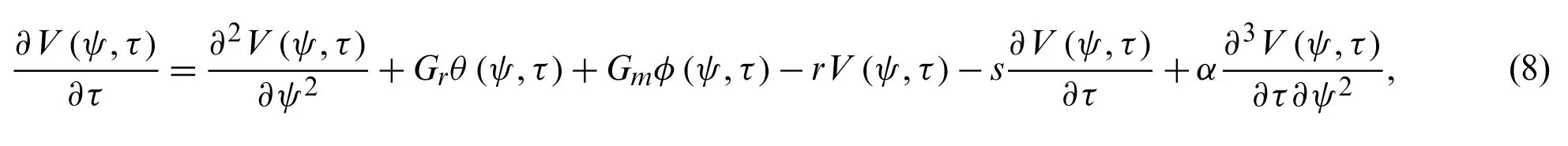
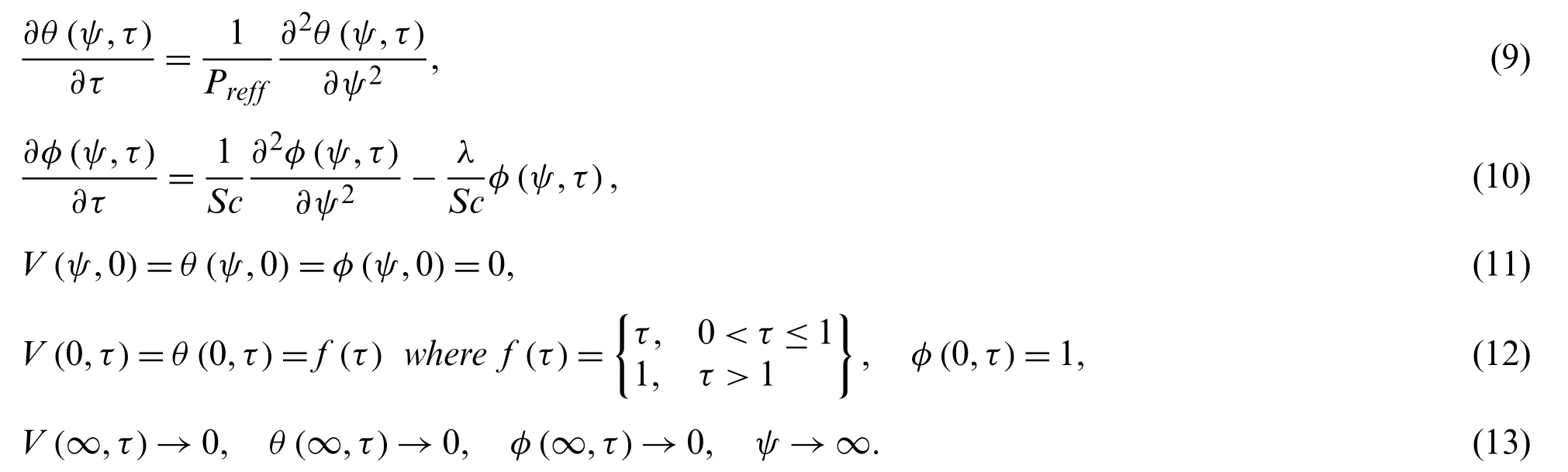
3 Exact Solution of the Problem

3.1 Solution of Heat Profile

Applying Laplace transformation to get the solution of Eq.(9)using Eqs.(11)–(13), we have

The solution of above Eq.(14)is

using appropriate conditions are used to find the value of constant,

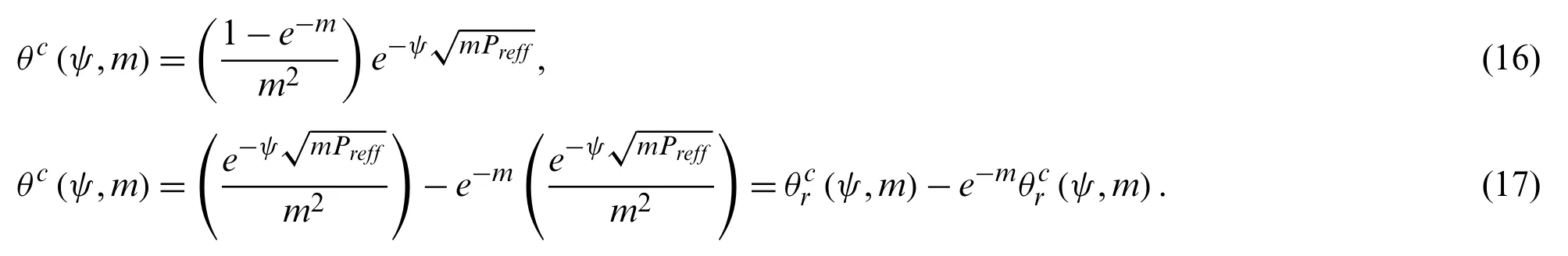
The inverse Laplace transformation of Eq.(17)is

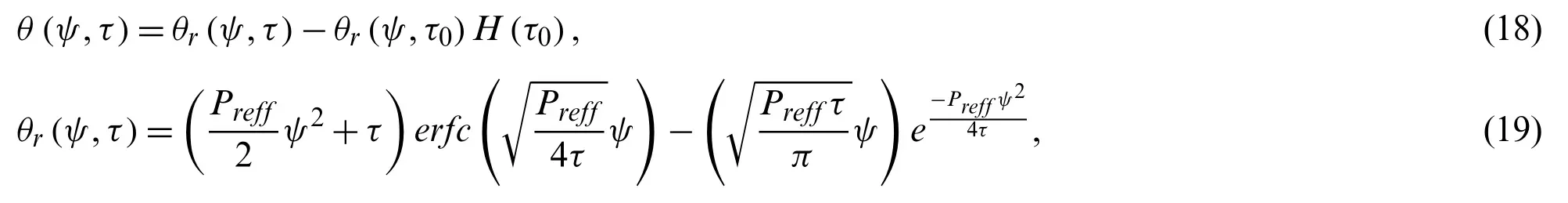
whereH(τ0)represent a standard Heaviside function withτ0=τ−1.

3.1.1 Nusselt Number

To estimate the rate of heat transfer can be obtained as

3.2 Solution of Mass Profile

Applying the Laplace transformation to Eq.(10)with suitable initial condition on concentration

The required solution of second order differential Eq.(21)with help of (11)–(13)on concentration is given by

To obtain the exact solution, we take the inverse Laplace transformation, we have

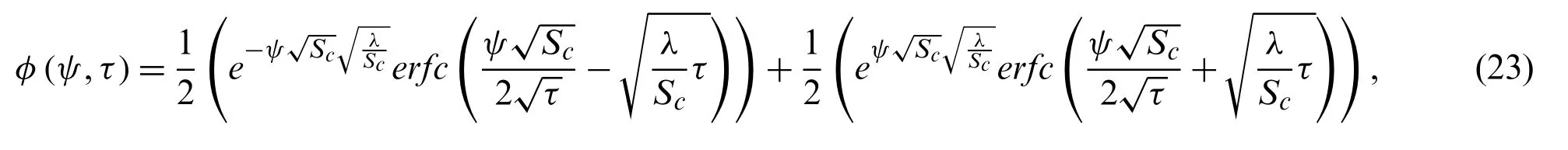
using from literature

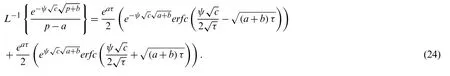
3.3 Solution of Velocity Profile

The solution of Eq.(8)by using Laplace transform, we have

by using the Eqs.(16)and (22)for the valuesθc(ψ,m)andφc(ψ,m), the solution of Eq.(25)can be written as

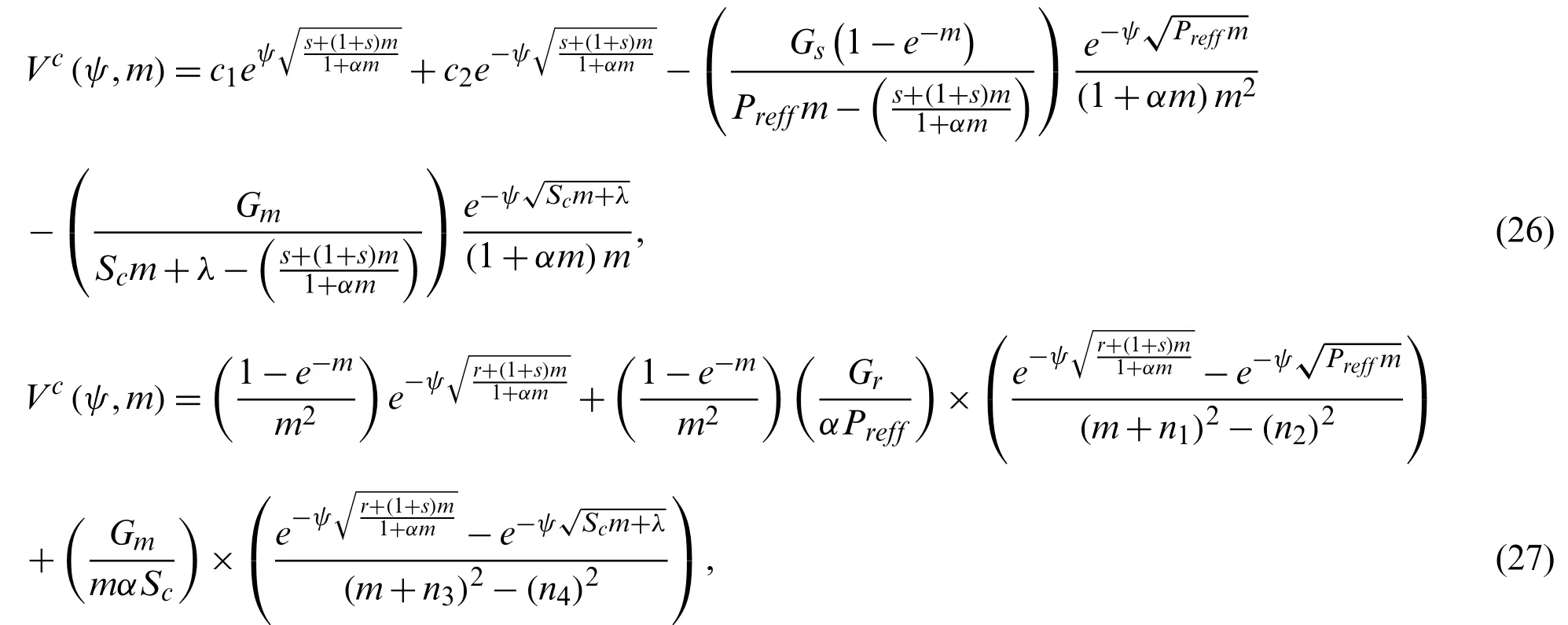
where

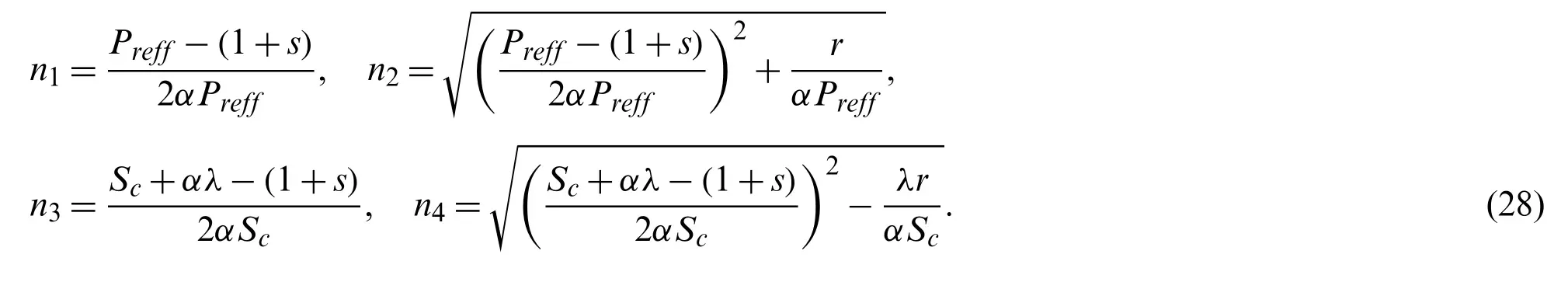
Eq.(27)can be written as in the following form:

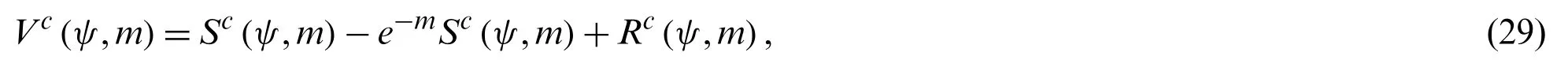
where

Further,Sc(ψ,m)can be written as

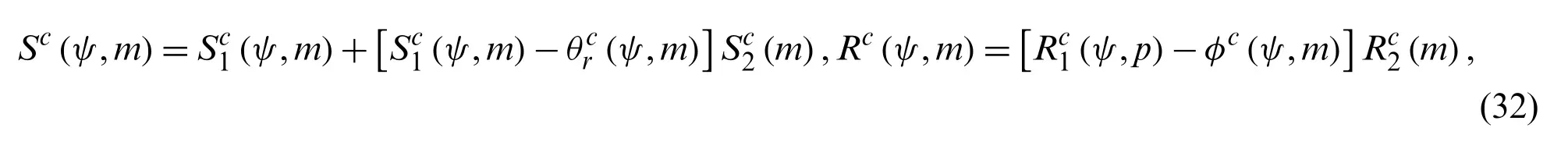
where

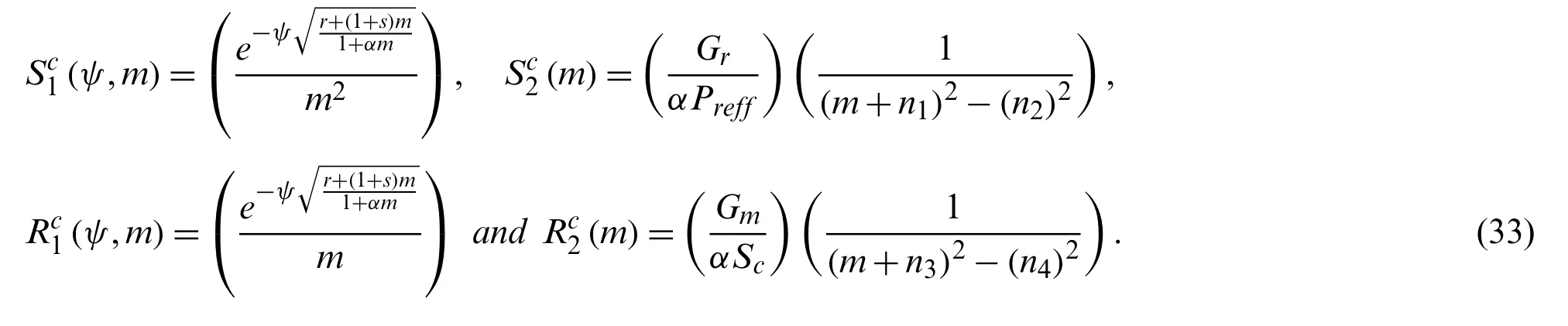
Applying inverse Laplace transformation with convolution product on Eq.(32), we get the required solution

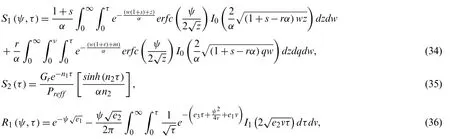
Substituting all the above functions, the equation of velocity field becomes in the form

3.3.1 Skin Friction

The following relation used to calculate the skin friction as

4 Limiting Cases

We recover the same result for velocity field in the absence of mass Grashof numberGm=0 obtained by Anwar et al.[28].Also whenNr= 0 andGm= 0, we get the same expression for velocity as discussed by Samiulhaq et al.[34].

5 Graphical Discussion

This part is devoted for physical interpretation of heat transfer is executed on the motion of Second-grade fluid near a porous surface.The impact of thermal radiation, magnetic field,and ramped temperature conditions are also analyzed via Laplace integral transform to obtain a unique and exact solution.The graphical representations are depicted for showing the impact of physical parameters such asPr,Nr,Sc,Gm,Gr,KandMon energy, concentration and velocity profile.Fig.2 is plotted for the impact ofPron energy profile.It is seen that thermal layer and temperature decreases by large value ofPr.AsPrincrease, the temperature profile reduce more rapidly.Physically, for less value ofPrheat conductivity enhances.Fig.3 shows the impact of heat radiationNr.By enhancing the value ofNr, the required energy enhance.The domination ofNr, enhanced due to transportation of energy.

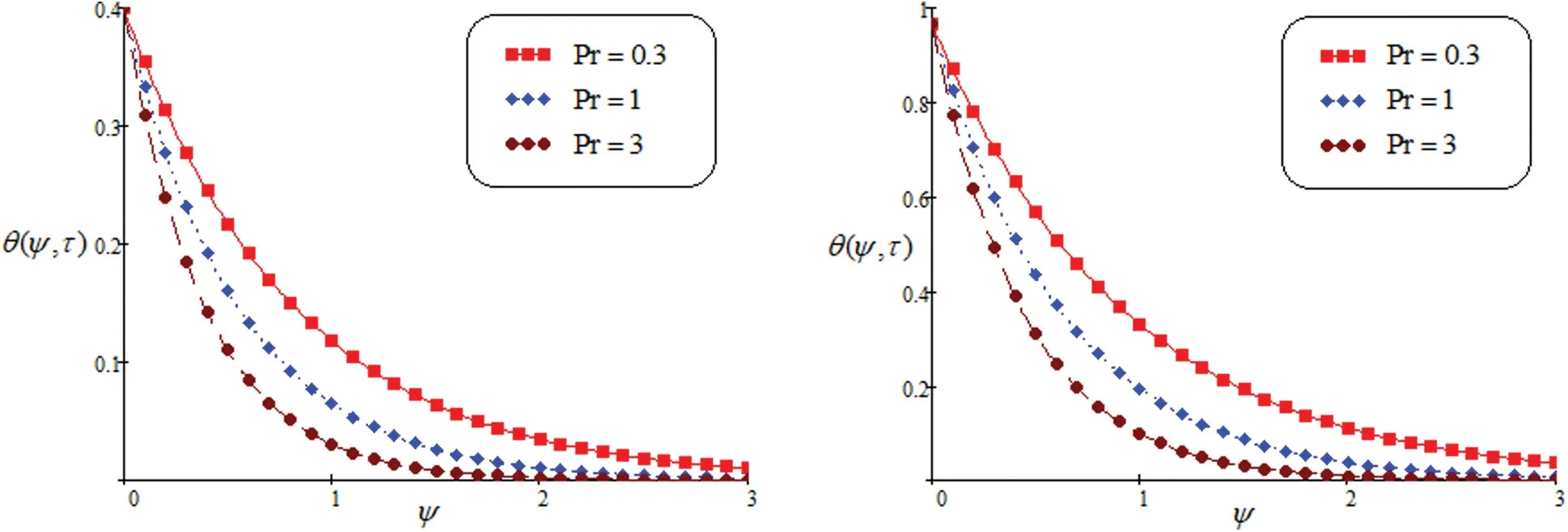
Figure 2: Temprature for altered values of Pr

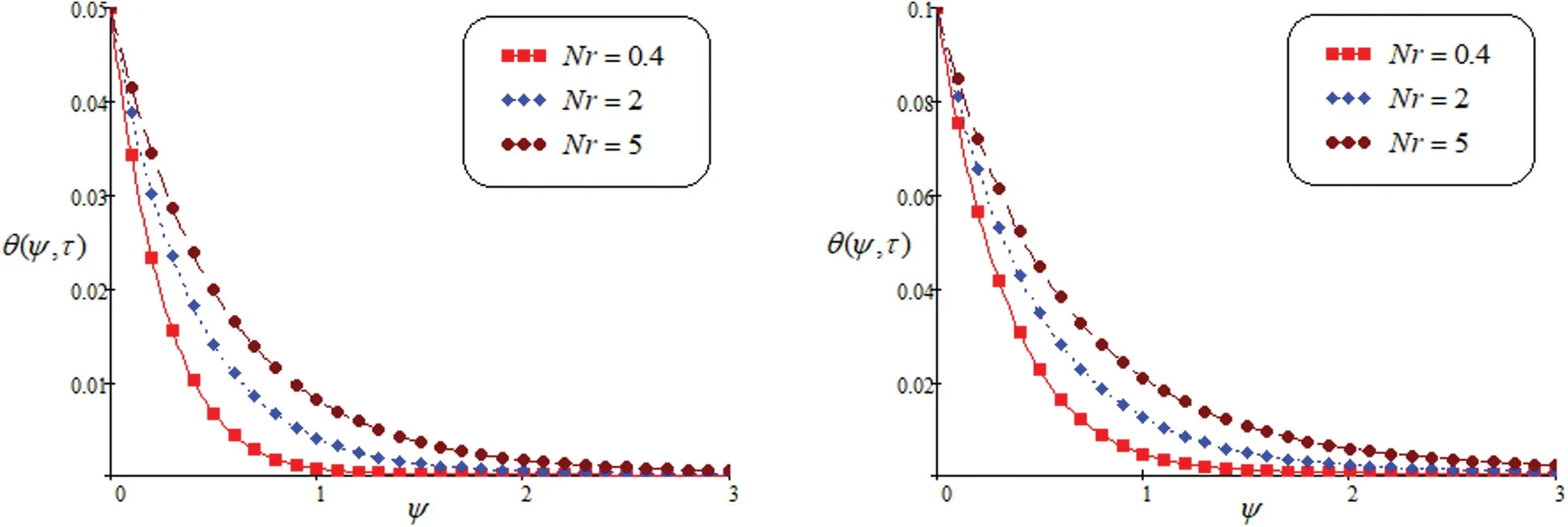
Figure 3: Temprature for altered values of Nr

In Figs.4 and 5, we discussed the behavior ofλandScon concentration profile.It is noted that the greater value ofλ, the concentration is increasing while in case ofSc, the concentration reduce as enhance the value ofSc.Contribution of concentration component on the fluid motion is important and it cannot be ignored.

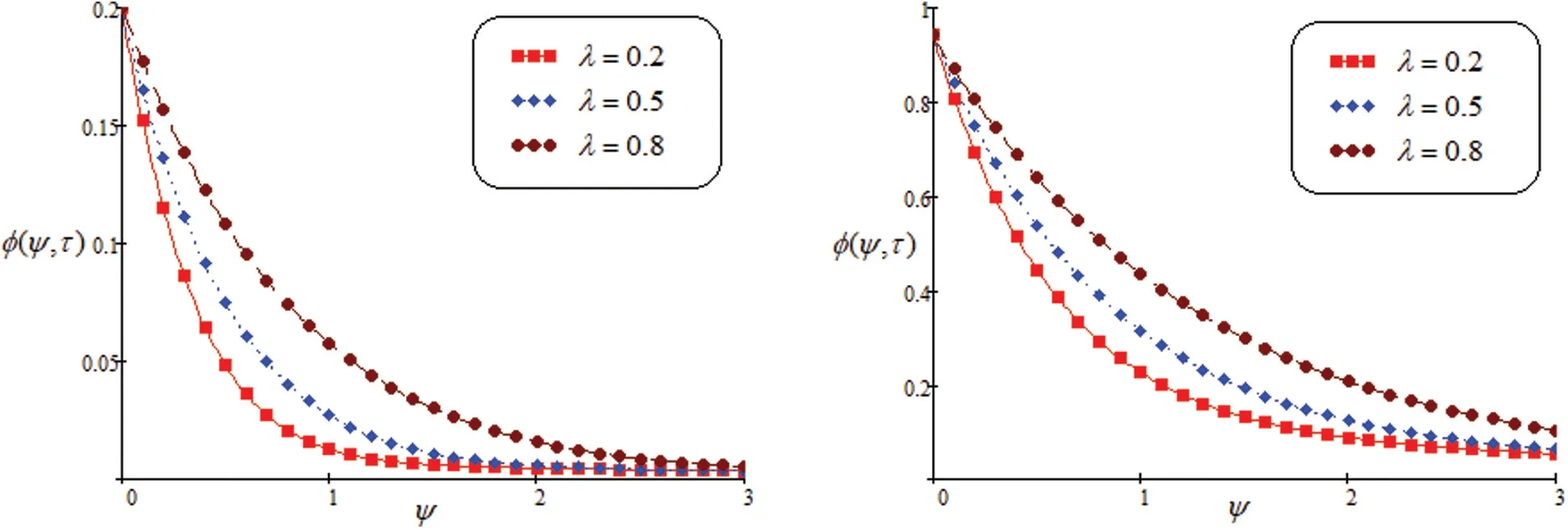
Figure 4: Concentration for altered values of λ

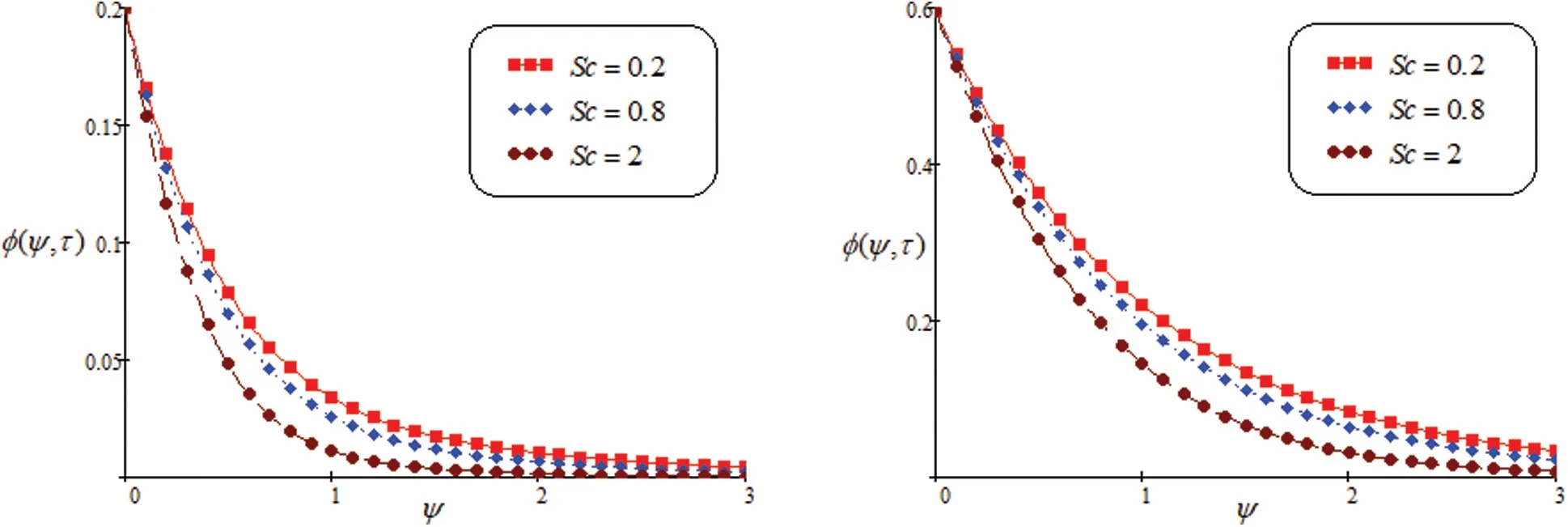
Figure 5: Concentration for altered values of Sc

Fig.6 shows the influence ofGm.It is the ratio of mass force to viscous force, which causes free convection.It is noted that the fluid velocity is increasing, if we increase the value ofGm.Fig.7 shows that the impact onGrfor velocity field.The curve behavior ofGris same asGm.It is noted that the velocity field enhance by increasing inGr.Physically, when theGris increased,then fluid flow increase due to the thermal effects.

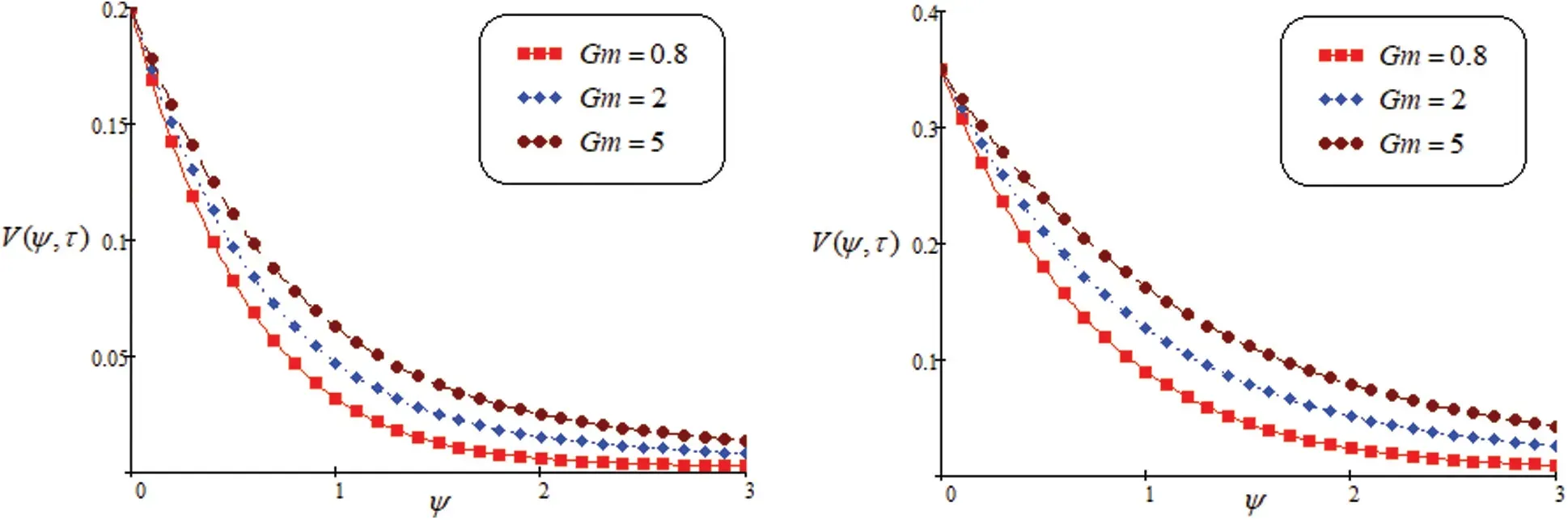
Figure 6: Velocity for altered values of Gm

Figure 7: Velocity for altered values of Gr

Fig.8 shows the effect of permeability on velocity curve.The fluid velocity enhance as escalate the value ofK.Fig.9 discusses the domination ofMon the velocity curve.These graphical representation indicates that an increase inM, the velocity reduce due to Lorentz force.It behave as a drag force.By increasing the parameter of magnetic field, the Lorentz force also increase.Fluid flow on the boundary layer is slow down due to this force.Fig.10 discusses the behavior ofPr.Specific heat and conductivity are depend onPr.The thickness of momentum and boundary layer is controled by prandtl number.It seen from the graph, decreasing the velocity,observed by increase the value ofPr.The lower prandtl number enhance the thermal conductivity and increase the boundary layer.Fig.11 shows the impact ofScon fluid profile.It notices that the value ofScenhance, the velocity of fluid flow decreased.

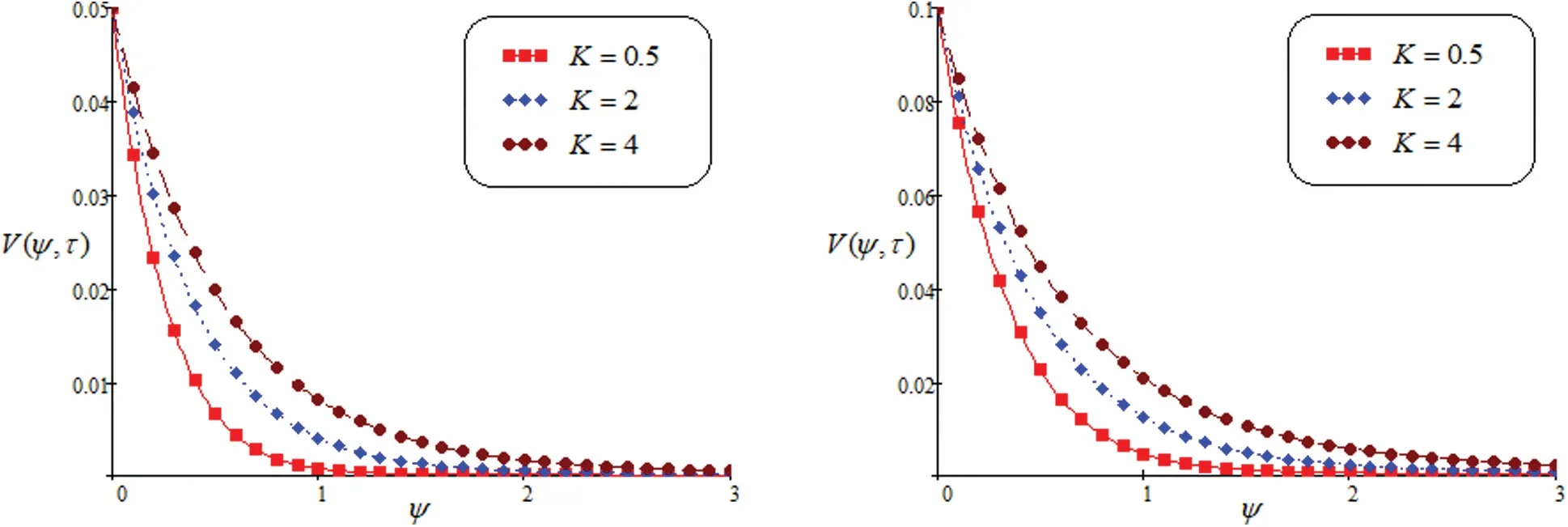
Figure 8: Velocity for altered values of K

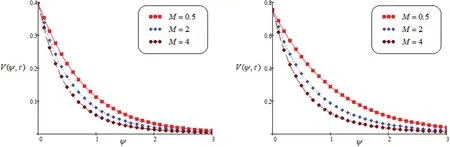
Figure 9: Velocity for altered values of M

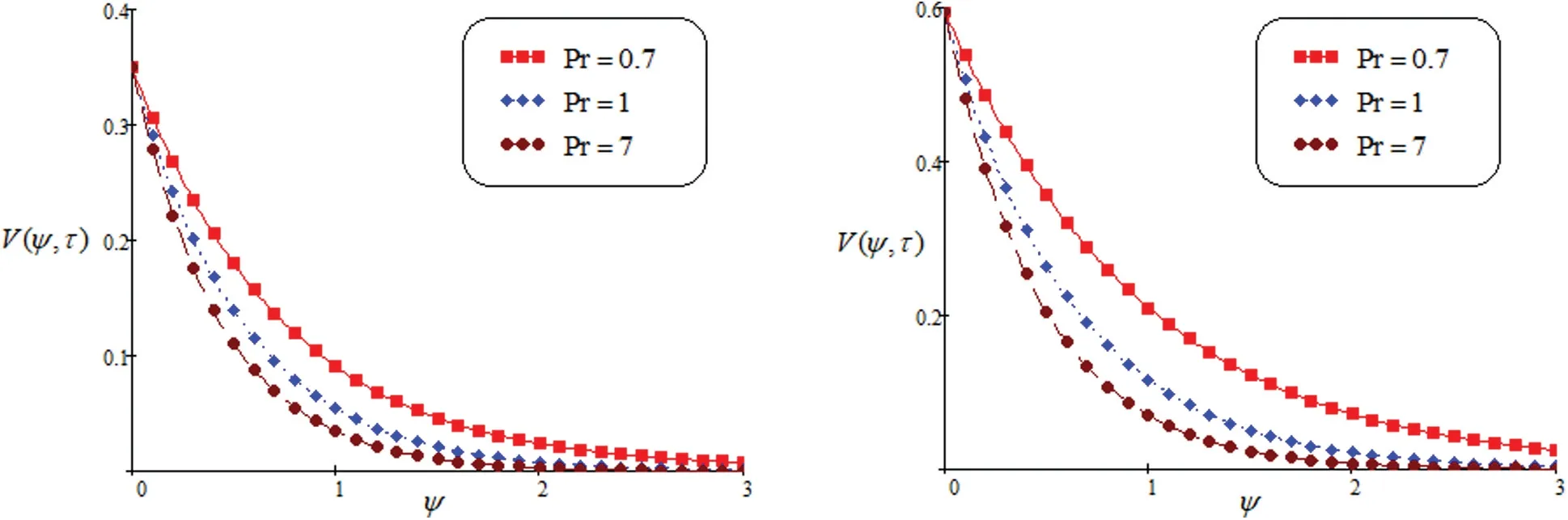
Figure 10: Velocity for altered values of Pr

Figure 11: Velocity for altered values of Sc

6 Concluding Observation

This part is devoted for dynamical analysis of heat transfer on MHD Second-grade fluid near a porous surface.The impact of ramped temperature condition and magnetic effect are analyzed via Laplace integral transform to obtain a unique and exact solution of velocity profile.Some significant remarks and concluding results are given below:

• It is noted that the decay in temperature for increasing value ofPrwhile temperature is increasing as increase inNr.

• The decay in concentration for growing the values ofSc.

• The fluid velocity decreases when the value ofMincreased.

• Enhance the values ofGr,Gm, the required fluid velocity is increasing.

• Enhance the values ofK, the required fluid velocity is increasing.

• In case of large value ofScand magnetic fieldMthe fluid velocity is decelerated.

• Contribution of concentration component of fluid velocity on the fluid motion is important and it cannot be ignored.

Acknowledgement:The authors are highly thankful and grateful for generous support and facilities of this research work.

Funding Statement:Self supported by the authors.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.