Modelling of Contact Damage in Brittle Materials Based on Peridynamics

Jingjing Zhao,Guangda Lu,Qing Zhang and Wenchao Du

1Nanjing Institute of Railway Technology,Nanjing,210031,China

2Tongji University,Shanghai,200092,China

3Department of Engineering Mechanics,Hohai University,Nanjing,211100,China

4Nanjing High Speed Gear Manufacturing Co.,Ltd.,Nanjing,211100,China

ABSTRACT As a typical brittle material,glass is widely used in construction,transportation,shipbuilding,aviation,aerospace and other industries.The unsafe factors of glass mainly come from its rupture.Thus,establishing a set of prediction models for the cracks growth of glass under dynamic load is necessary.This paper presents a contact damage model for glass based on the ordinary state-based peridynamic theory by introducing a contact force function.The Hertz contact(nonembedded contact)problem is simulated,and the elastic contact force is determined by adjusting the penalty factor.The proposed model verifies the feasibility of penalty-based method to simulate the contact problem of glass.The failure process of glass specimen under impact is simulated, where two loading methods, the drop ball test and the split Hopkinson pressure bar are considered.Numerical results agree well with the experimental observations,thereby verifying the effectiveness of the proposed model.

KEYWORDS The ordinary state-based peridynamic; glass; numerical simulation; contact damage; impact failure

1 Introduction

Glass is a highly homogeneous brittle material and it can be made into any shape and mass produced due to its homogeneity.Hence, glass materials are widely used in construction,transportation, shipping, aviation, aerospace and other industries.However, the glass is extremely easy to break when its surface is subjected to impact load.Effectively revealing the mesoscopic failure mechanism of glass under low-velocity impact loads is of great importance to improve its resistance and safety.

In the early days, many scholars investigated the damage of glass under impact, mainly focusing on the crack initiation, propagation, and crack development patterns of glass through a series of experimental studies [1–6].In 1931, Andrews [1] pointed out that a force threshold is found for the crack formation of glass under impact load.Roesler [2] considered the conical indentation of a glass specimen and measured its fracture energy to verify Griffith [3] energy balance condition for brittle material cracking.Knight et al.[4], Chaudhri et al.[5] studied the crack development patterns of glass under medium and high-speed loading by changing the impact velocity of iron ball.The results show that the crack appears in the non-loading section,and the Hertzian cone angle of the crack zone varies with the loading speed.Ball et al.[6]observed that glass specimens exhibit a star-shaped fragmentation failure mode under low-speed conditions.In recent years, Bouzid et al.[7], Nyongue et al.[8], and Daryadel et al.[9] conducted relevant quantitative experimental analysis on the dynamic response and fracture criterion for glass under impact loading.The failure mechanism for different types of glass is realized in the work of Kumar et al.[10].These test results reveal the response law and failure mechanism of glass as a typical brittle material under impact load from different aspects.

With the development of computers, numerical simulation methods have been widely used to reproduce and explain the phenomena observed in experiments.Numerical models based on traditional continuum mechanics, such as finite element method [11] and boundary element method [12], are gradually used in many experimental studies.However, for discontinuities, such as crack bifurcation in solid materials and structures, traditional numerical methods are faced with the problems of singularity and low computational efficiency.The use of grid reconstruction [13]or the method of adding a cohesive element [14] in the finite element would cause to griddependent results.The partition algorithm [15] and fictitious crack model [16] adopted by the boundary element method (BEM)have similar limitations to the finite element method in the analysis of crack propagation problems.Therefore, researchers have proposed the extended finite element method [17].Compared with the traditional finite element method, it reduces the strict requirements on the mesh discontinuity.However, in the construction of enrichment function, the extended finite element method needs to know the characteristics of the problem to be solved in advance.This condition is relatively demanding for complex problems, such as crack branching and multi-crack intersection.In recent years, many researchers have studied the contact damage of brittle materials under impact load.Oliveira et al.[18] proposed an alternative BEM formulation to model the cohesive stresses through the domain term of the direct integral.Wang et al.[19]proposed a field-enriched finite element method to simulate the failure process of rocks.Kouet et al.[20] presented a bonded-particle methodology to investigate the crack growth and crack branching.Bo et al.[21,22] developed some explicit Galerkin formulations which can capture ductile fractures during high-speed impacts and simulate fracture of a plate under impact loads.

To solve contradiction between the continuity assumption and the discontinuity phenomenon of the failure problem, Silling [23] proposed a nonlocal method called peridynamics (PD)[24]to described the motion process of the material points through an integral equation.In the development of the peridynamics, researchers have conducted numerous quantitative analyses on the brittle fracture of polycrystalline materials [25], impact failure of shale materials [26],and the thermal brittleness and failure of glass plate under impact [27–29], and the problem of interaction between ice and seawater [30].Those results show that peridynamics does not have the singularity problem when analyzing the failure problem and can simulate the whole process of the material, including macroscopic crack initiation, propagation, and final failure.The above simulation of failure is based on the bond-based peridynamics theory (BBPD).However, bond-based peridynamics theory has some problems, such as the limitation of Poisson’s ratio and the lack of connection with traditional continuum theory.Silling et al.[31,32] proposed an ordinary state-based peridynamic theory (OSBPD)and a non-ordinary state-based peridynamics(NOSB PD).Both of them inherit the advantages of BBPD for solving discontinuous problems, and have a similar definition of state quantities to traditional physical quantities.To address the limitations of material calculation scale.Breitenfeld et al.[33], O’Grady et al.[34], and Chowdhury et al.[35] supplemented and developed the OSBPD theory.Song et al.[36] proposed a state-based peridynamic model by using adaptive particle refinement to simulate the formation of water ice crater under impact loads.Zhou et al.[37] developed a 2D elastoplastic model of the ordinary state-based peridynamic theory to analyze the plastic zone of the crack tip of rock material.Wu et al.[38] proposed a concrete impact failure model based on NOSBPD theory.In recent years, many scholars began to study the contact model based on PD method.Xin et al.[39]developed a NOSBPD model for brittle fracture to simulate the edge-on impact and drop ball test and discussed the contact algorithm between the projectile and target.Littlewood et al.[40] summarized the simulation results of finite element method and peridynamics.A combined approach of finite element method and peridynamics is utilized via a contact algorithm.Ye et al.[41]proposed a continuous contact detection algorithm to simulate the brittle failure behavior of ice during the contact between propeller and ice.This algorithm can well capture the ice damage characteristics.Kamensky et al.[42] summarized several existing peridynamic contact friction models and introduced a state-based nonlocal friction formulation to demonstrate the properties of various peridynamic contact models through some impact and penetration problems.Silling et al.[43] proposed a new PD model to simulate the elastoplastic response, creep, and fracture.In the case of small deformation, this model is consistent with classical Hertz contact analysis.Wang et al.[44] proposed a 3D conjugated bond-pair-based peridynamic model to simulate the failure characteristics of rock materials with different forms of central fissure.

This paper presents a new contact damage model based on the OSBPD theory for glass by introducing a contact force function.The arrangement of the rest sections is as follows.In Section 2, the governing equations based on OSBPD theory are described in brief, followed by the contact model and algorithm.In Section 3, the Hertz contact (nonembedded contact)problem is simulated, and the elastic contact force is determined by adjusting the penalty factor.The proposed model verifies the feasibility of penalty-based method to simulate the contact problem of glass.In Section 4, the failure process of glass specimen under impact is simulated, and two loading methods, drop ball test (DBT)and split Hopkinson pressure bar (SHPB), are considered.The numerical results agree well with the experimental results, which verifies the effectiveness of the proposed model.

2 Methodology

2.1 Fundamentals of Peridynamics Theory

whereyis the position of particlexafter deformation.The force state vector betweenxandx′can be defined as

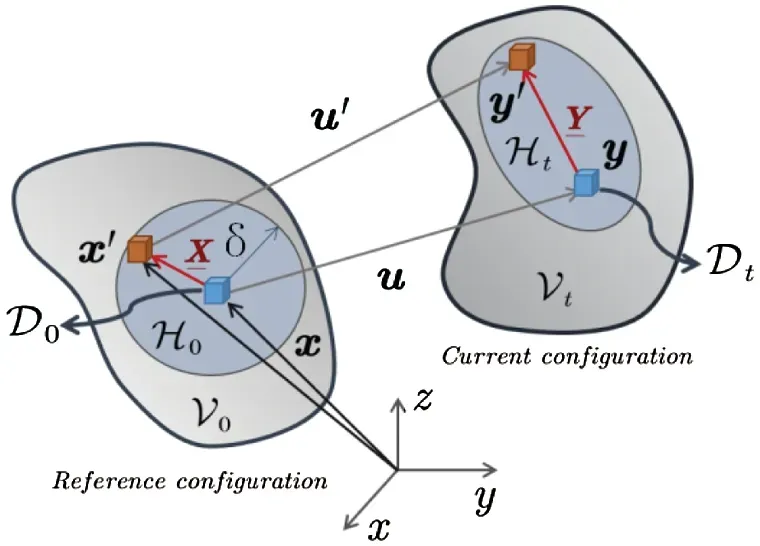
Figure 1: Reference configuration of particle movement

Therefore, a momentum balance equation at particlexis defined as

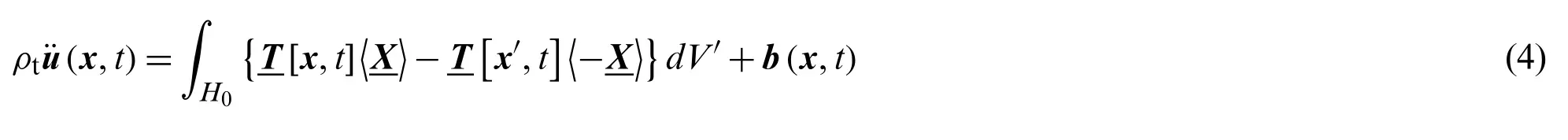
The above formula is the governing equation of peridynamics [31,32], and its above derivation shows that the peridynamics theory still belongs to the Lagrangian system.The difference from the traditional continuum mechanics is that it considers the nonlocal interaction between the particles.

whereσis the stress tensor.

2.2 Force State of State-Based Peridynamics Theory

The volume dilatationθis defined as

In accordance with elastic mechanics, the extension scalar statecan be decomposed into isotropic part

and deviatoric part

Therefore, the elastic energy density contains two parts

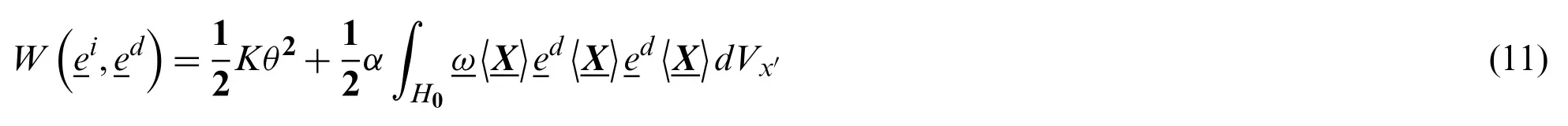
Correspondingly, the scalar forcetcan be expressed as

In accordance with the energy equivalence between the deformation energy density (11)and the strain energy density of classical elasticity,tcan be obtained as [31]

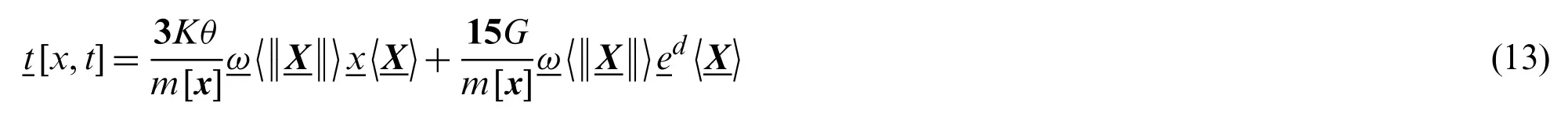
The above formula is the force state of state-based peridynamics theory, which includes traditional material parameters, such as bulk modulusKand shear modulusG.For the damaged material points, the scalar function [23] is defined as

whereμis a scalar function, and it is defined as

wheresis the fracture judgment parameter ands0is the corresponding critical value.If the extension scalar state is selected as the basis for judging whether the bond between two material points is broken, thensands0are defined as

whereG0[45] is the energy release rate.For the local damage defined by Eq.(14), the damage between material point pairs is shown in Fig.2.

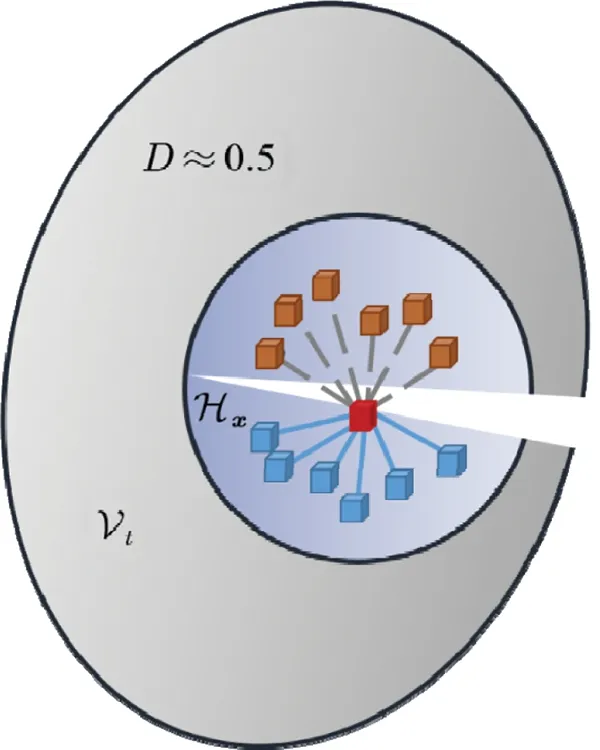
Figure 2: Damage between material point pairs when D ≈0.5

2.3 Contact Model of Peridynamics

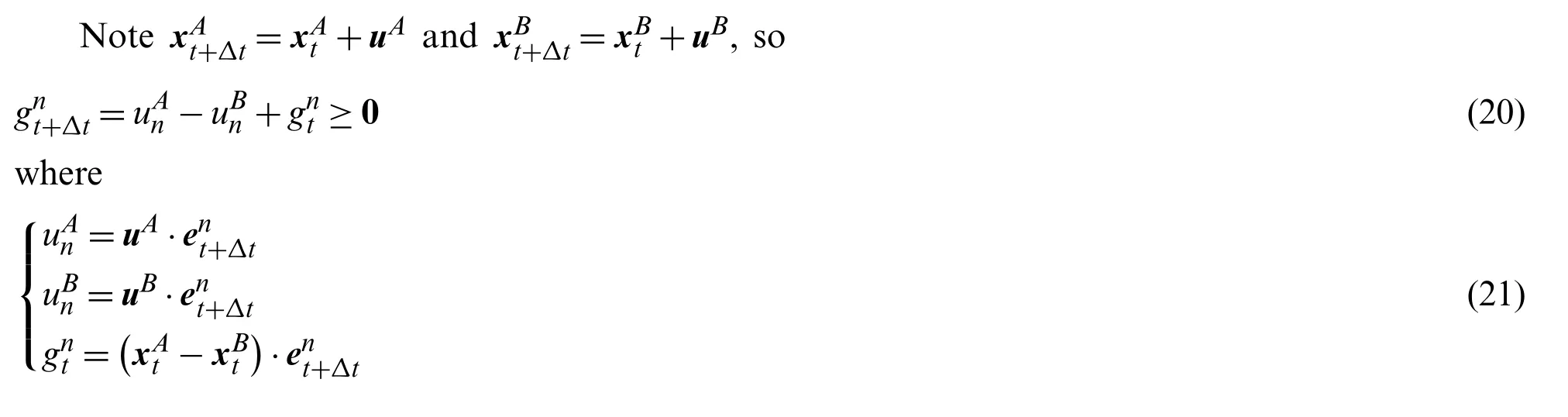
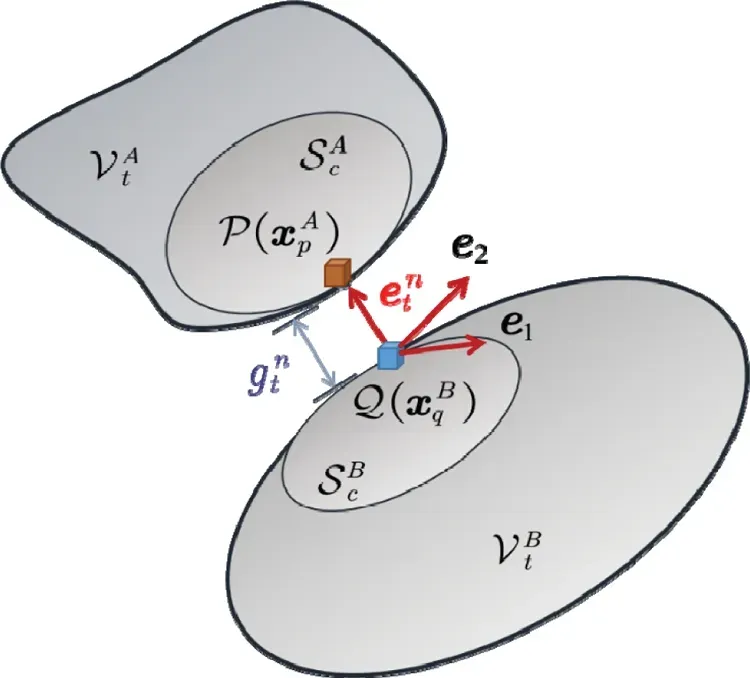
Figure 3: Contact point pair and the distance between them

The energy function, which includesAandBsystems, is expressed as

whereΠ0is the energy function without considering the contact force and contact conditions.ForAandB,δΠ0=0, which is equivalent to the Eq.(7), whereΠcfis the potential energy function of contact force.These contact forces are the acting force and reaction force.Thus, we have

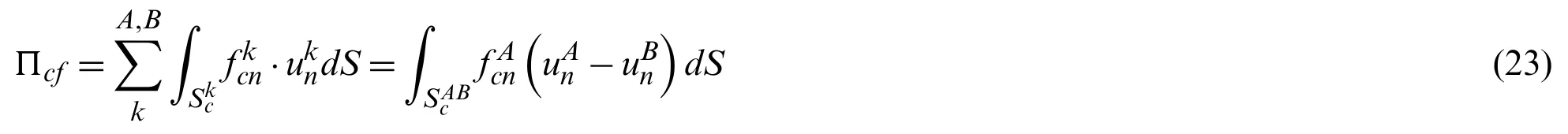
wherecnis the penalty factor.LetδΠ=0, we have

For a certain contact deformation body, if its contact surface isSc, then the contact force is

wherefc=(fc1fc2fcn)Tandfc1=fc2=0.Once the object is in contact, the contact force is applied to the material point on the contact surface in the form of body force density, that is

The contact force is related to the selection of the penalty factor.In theory, the larger the penalty factorcn, the higher the calculation accuracy, and the closer to the nonpenetration condition.This condition will be discussed in detail in the numerical solution process and specific examples.The penalty factor is collectively referred to as the contact force modulus in this paper.

2.4 Numerical Discretization and Solution

Regarding the spatial discretization, peridynamics divides the material uniformly into a cubic lattice of side length Δx, and the volume for any material point is ΔV(Fig.4).Therefore, all material points inH0can be defined as

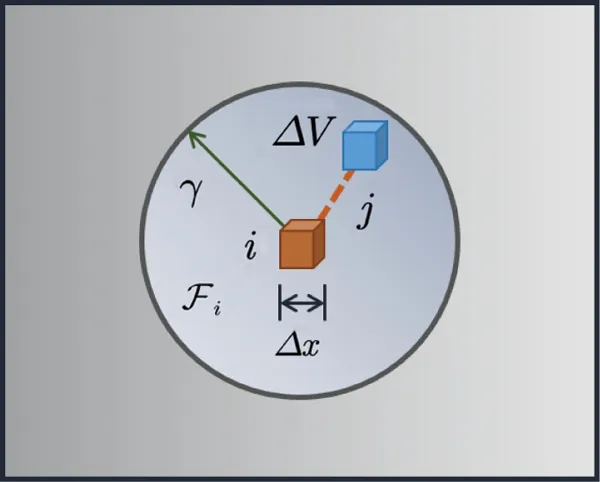
Figure 4: Discretization of spatial domain

Correspondingly, the discretization of the motion equation considering the contact force in the space domain is

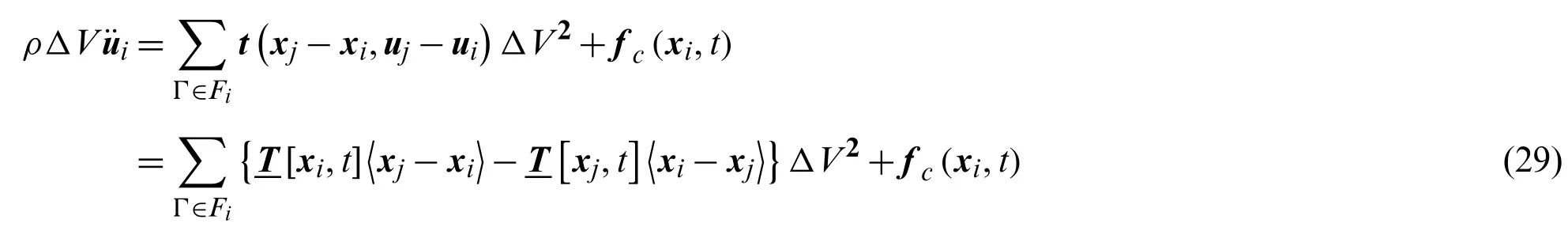
Similar discrete operations are applied to the weighted volumem[x] and volume dilatationθ.

Let=u(xi,tn)and time step Δt=tn−tn−1.The the formula of central difference scheme is obtained as

Substituting the above formula into the Eq.(29).Thus, we have

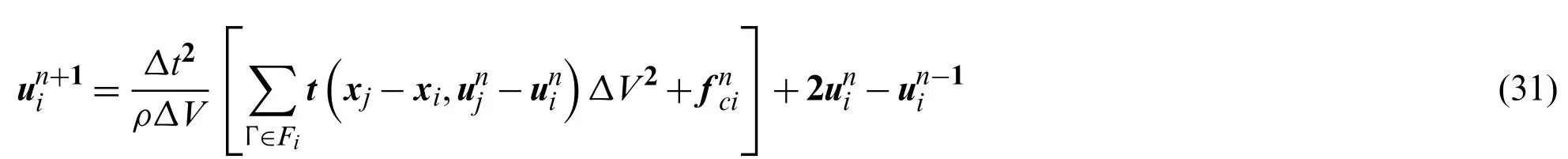
The time step should satisfy [33]

The virtual rigid “spring” is added, that is, the rigidity of contact areaScis improved.Eq.(33)is modified as

The value of penalty factorscnis discussed in the following calculation examples.

3 Verification of the Elastic Contact Problem

The Hertzian contact (no embedded contact)is considered, as shown in Fig.5.The size parameters of the deformation body areL=B=1.6mandH=0.8m.The elastic modulus and Poisson’s ratio of the material areE=10 GPa andν=0.25.The mass density isρ=2400 kg/m3.The radius of the rigid sphere is set asR= 0.2 m, and 2R/L≤3 approximately satisfies the assumption of semi-infinite deformation body.The fixed horizon size is set asδ=3Δx.The time step is set as Δt=1×10−7s.For the theoretical solution of this problem, the derivation can be found in the Appendix.

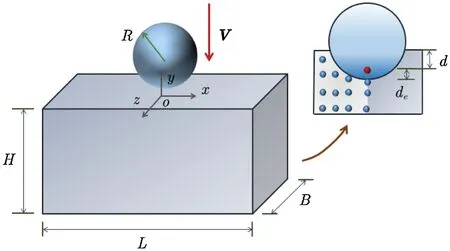
Figure 5: Hertzian contact problem

When the rigid sphere is in contact with the deformable body at a constant speedv=10 m/s(it can be regarded as a quasi-static problem),cn=5×106,1×107,5×107,1×108,5×108,1×109are used for calculation to analyze the influence of contact moduluscnon the result.The discrete distance of the deformable body is set asΔx=0.01 m.The results of embedded distancedeand contact forceFccorresponding to indentation depthdare shown in Figs.6 and 7.As shown in Figs.6 and 7, the contact force gradually approaches the theoretical solution with the increase in contact moduluscn.Therefore, for non-embedded contact problems, the value of contact moduluscnshould be as large as possible to satisfy the computer truncation error and the stability requirements of differential solution.

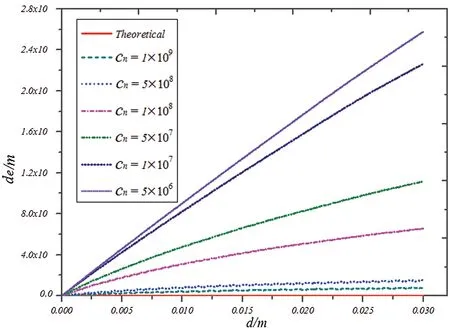
Figure 6: Graph of embedded distance de corresponding to indentation depth d

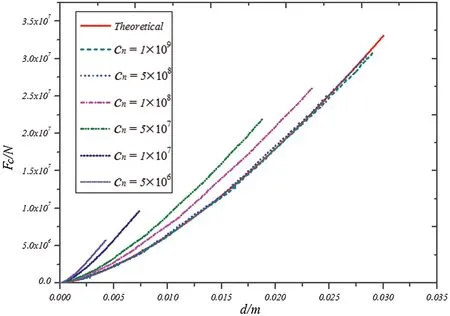
Figure 7: Relationship between contact force Fc and indentation depth d

For the case ofcn=1×109, the displacement nephogram of deformation body inydirection at timet=1×10−3,2×10−3,3×10−3s is drawn in Fig.8.For the contact problem of a rigid sphere, the contact surface is arc-shaped, and its displacement decreases outward along the center of the contact surface, which is also consistent with the actual situation.

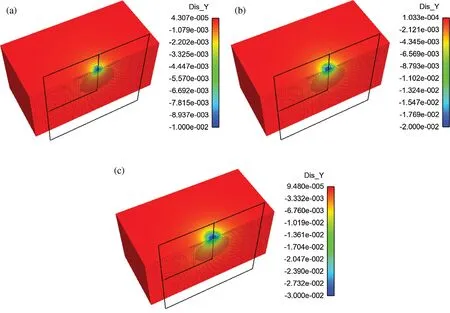
Figure 8: Displacement profile of the deformable body (a) t=1×10−3 s (b) t=2×10−3 s (c)t=3×10−3 s

The discrete distance is still set asΔx=0.01 m, and the contact modulus is taken ascn=1×109.The radius of rigid sphere is changed by incrementΔR=0.05 m.When the indentation depth of the rigid sphere isd=0.02 m, contact forceFcis plotted in Fig.9.With the increase in radius of the rigid sphere, contact forceFcis closer to the corresponding theoretical solution.WhenR=0.15 m and the relative discrete size is set asΔχ=Δx/2R=1/30, the calculation error of contact forceFcis 6.9915%.WhenR=0.2 m andΔχ=1/40, the calculation error of contact forceFcdrops to 0.1377%.The calculation error of the contact force decreases with the decrease in the relative discrete size.The smaller the relative discrete size (the more discrete material points),the more time consuming the calculation.As shown in Fig.9, the effect of improving the error is unremarkable when the relative discrete size is less than a certain critical value.WhenR=0.2 m and the contact modulus of the rigid sphere is still taken ascn=1×109, change the discrete distance of the material points and takeΔx= 0.1,0.08,0.05,0.04,0.02,0.01 m.The calculation results are shown in Fig.10.A similar conclusion can be obtained, that is, the calculation error of the contact force gradually decreases with the decrease in distance between the material points.

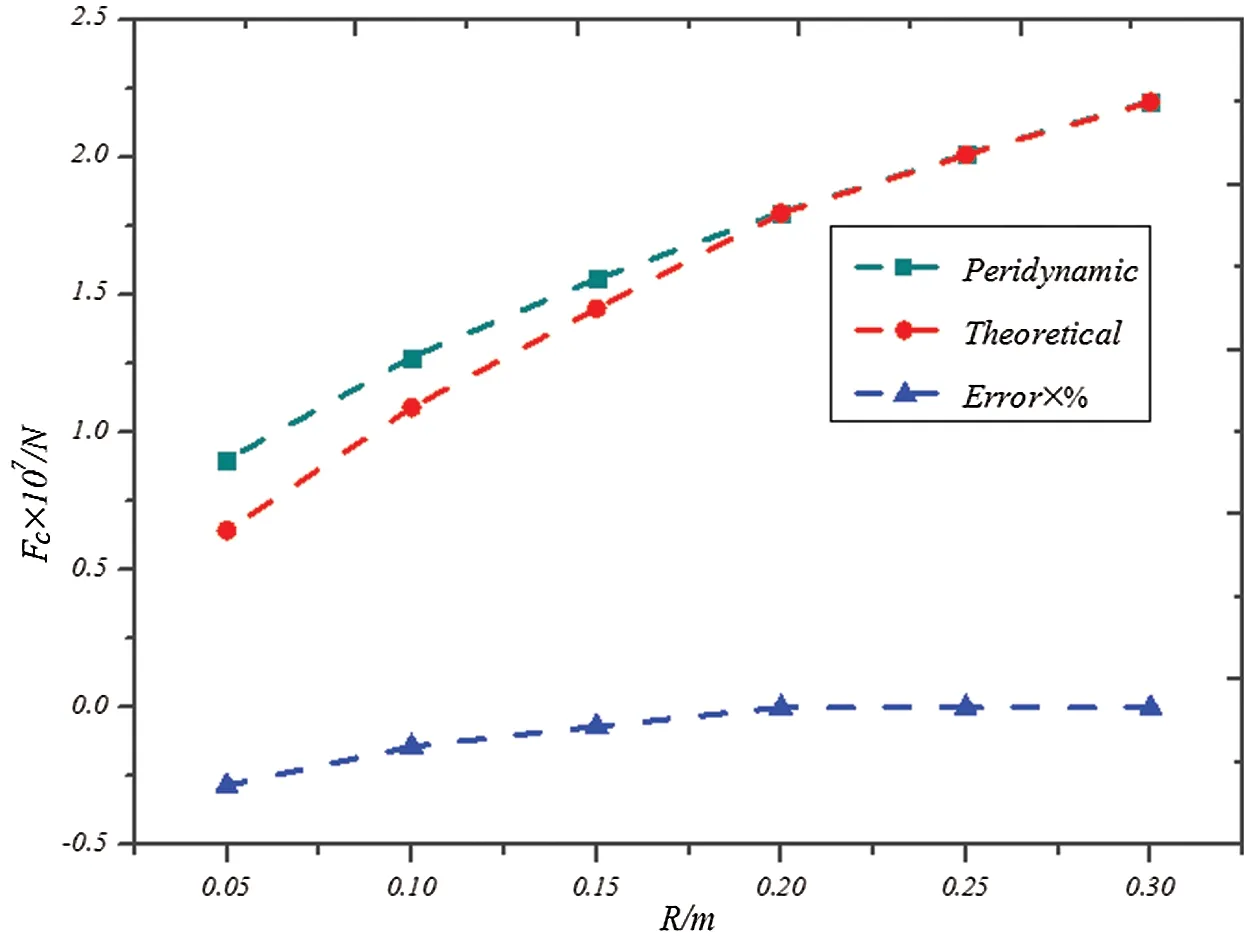
Figure 9: Plots of the contact force vs.the radius of rigid sphere

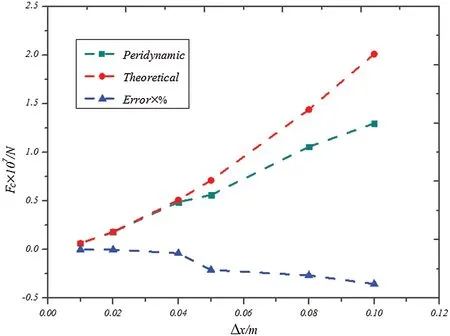
Figure 10: Plots of the contact force vs.the discrete distance

In summary, the influencing factors in the contact model of peridynamics are discussed and compared with the theoretical solution.The penalty-based method can be used to simulate the contact problem well by selecting the appropriate relative discrete size and the contact modulus.This process meets the requirements of computer truncation error and stable calculation.Therefore, on the basis of experience and the calculation results of this case, the calculation formula of contact modulus can be given as follows:

The range of adjustment coefficientαis from 1 to 50;Eis the elastic modulus;Δxis the discrete distance of material points.

4 Contact Failure of Glass Specimen under Impact

Float glass material [7] is selected for analysis.The elastic modulus isE= 70 GPa, the Poisson’s ratio isν=0.23, the mass density isρ=2508 kg/m3, and the critical energy release rate is set asG0=8 J/m2.The length and width of the glass sample are the same asL=B=100 mm,and the thickness isH=5 mm.For the simulations of DBT and SHPB, the models are shown in Figs.11 and 12.In the simulation of DBT, the mass of the iron ball is 55 gr.(3.564 g), and the mass density isρ=7860 kg/m3.The pressure bar is made of aluminum in the simulation of SHPB.Its elastic modulus isE=71 GPa, the Poisson’s ratio isν=0.33, and the mass density isρ=2900 kg/m3.

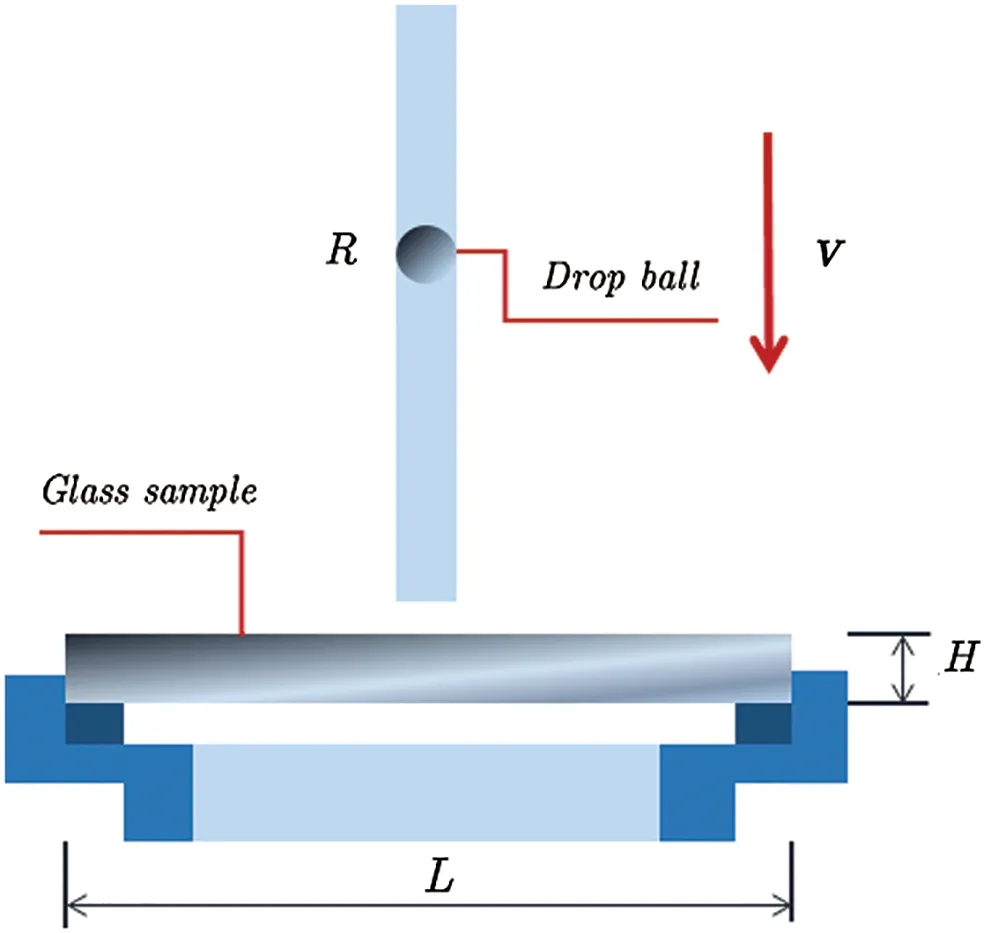
Figure 11: Geometric model of DBT [7]

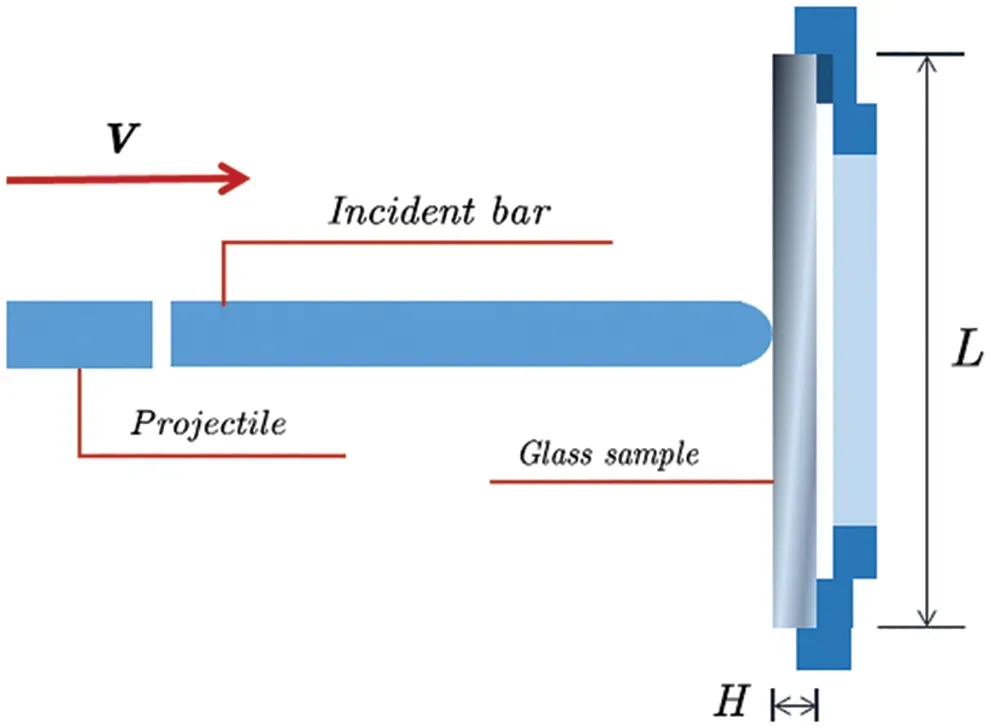
Figure 12: Geometric model of SHPB [7]

In the analysis of peridynamics, the contact modulus is taken ascn=1×109, and the discrete distance of glass samples isΔx=0.5 mm when the penalty-based method is used to calculate the above two models.The time step value isΔt=1×10−8s.The low loading rate of DBT and the high loading rate of SHPB are considered.The results are shown in Figs.13 and 14.For low loading rate (v=1 m/s)in Fig.13, the final damage form is mainly a small amount of fragments.For the high-speed impact of SHPB, the sample appears to be broken.The simulation results are in good agreement with the test results (Fig.15).

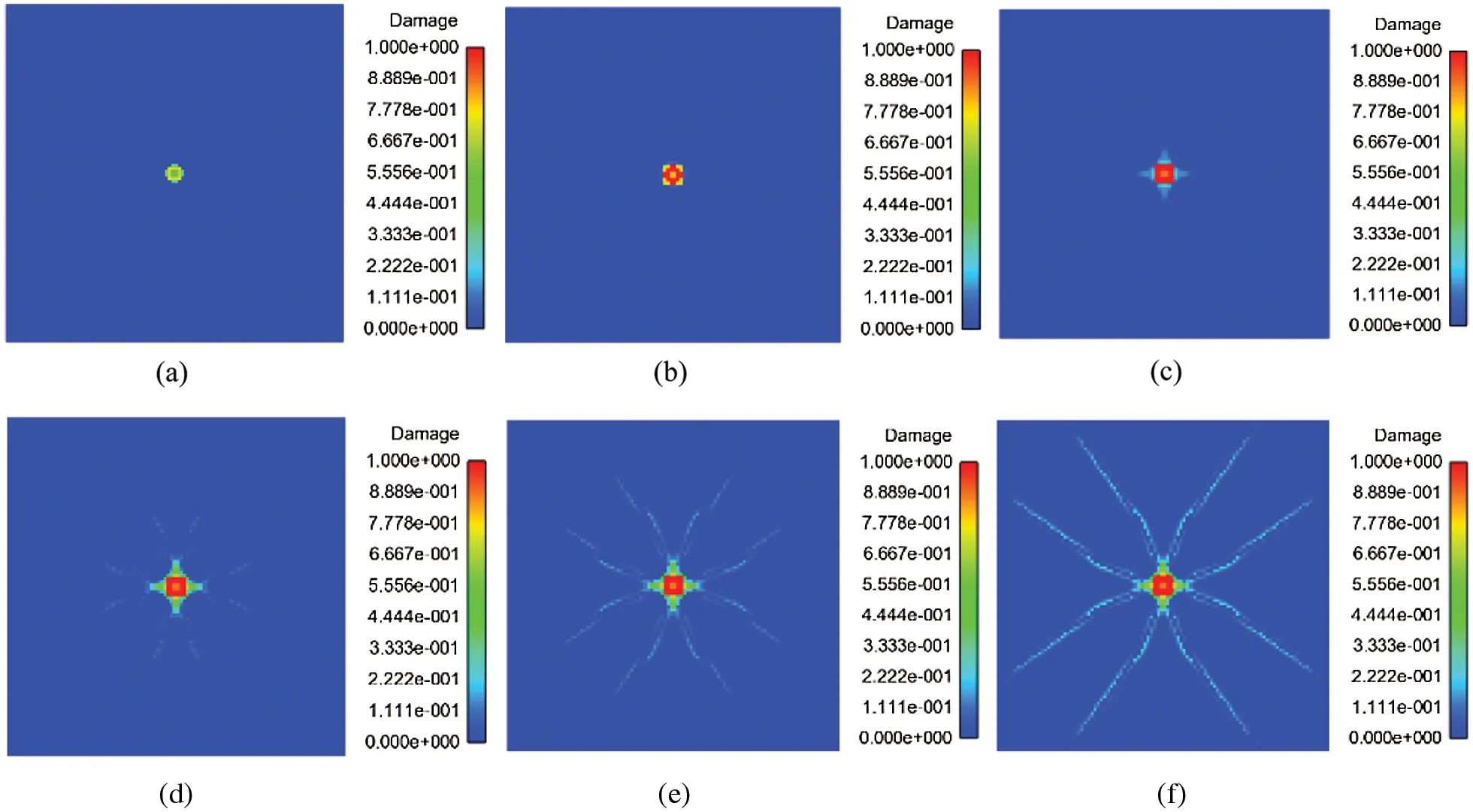
Figure 13: Damage of DBT model at different times (v=1 m/s)(a) t=1×10−5 s (b) t=2×10−5 s(c) t=3×10−5 s (d) t=4×10−5 s (e) t=5×10−5 s (f) t=6×10−5 s

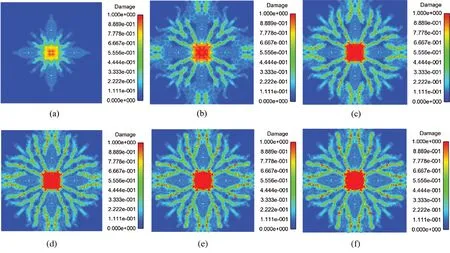
Figure 14: Damage of SHPB model at different times (v =20 m/s)(a) t=1×10−5 s (b) t =2×10−5 s (c) t=3×10−5 s (d) t=4×10−5 s (e) t=5×10−5 s (f) t=6×10−5 s

Figure 15: Experimental results [7] (a)Low loading rate of DBT (b)High loading rate of SHPB

Considering the low loading rate (v=3 m/s)of DBT and the high loading rate (v=30 m/s)of SHPB, the comparison between the two simulations and test results are shown in Fig.16.The proposed contact damage model can deal with the impact failure of glass qualitatively and quantitatively.The curve of contact forcevs.indentation depth is shown in Fig.17.The comparison of DBT and SHPB results by using different load rates shows that the impact speed increases with the increase in impact speed.

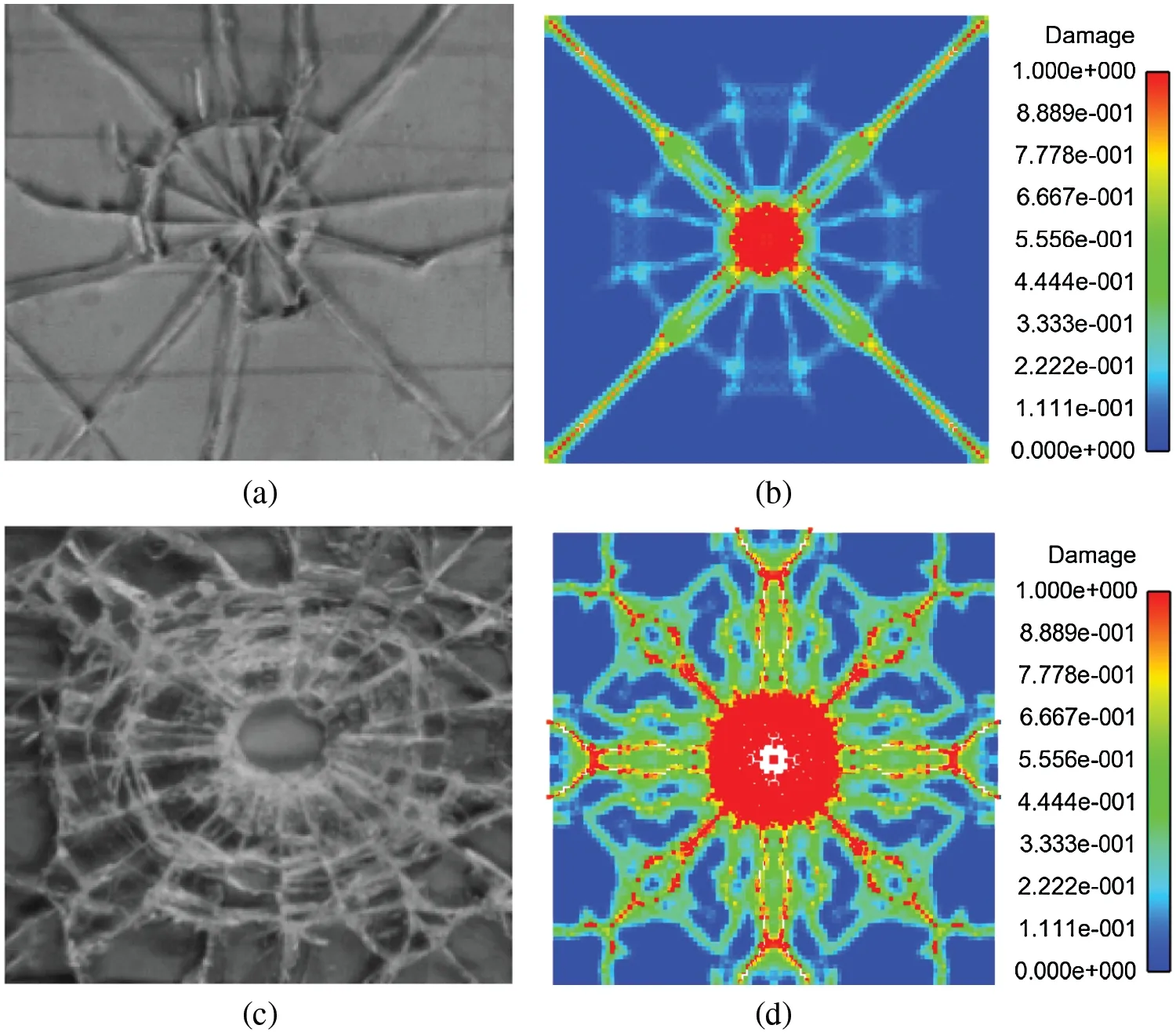
Figure 16: Comparison of experimental results and simulation results (a)Experimental results of DBT [7] (b)Peridynamics results of DBT (v=3 m/s)(c)Experimental results of SHPB [7] (d)Peridynamics results of SHPB (v=30 m/s)

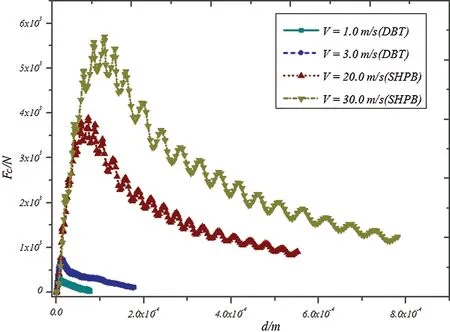
Figure 17: Curve of contact force vs.indentation depth at different impact speeds

The damage of glass specimens in different times is shown in Fig.18.With the increase in loading speed, the damage time becomes shorter, and the damage degree becomes more serious.The simulation results are consistent with the experimental results.Therefore, the contact model of peridynamics can well simulate the failure of brittle materials under impact conditions.

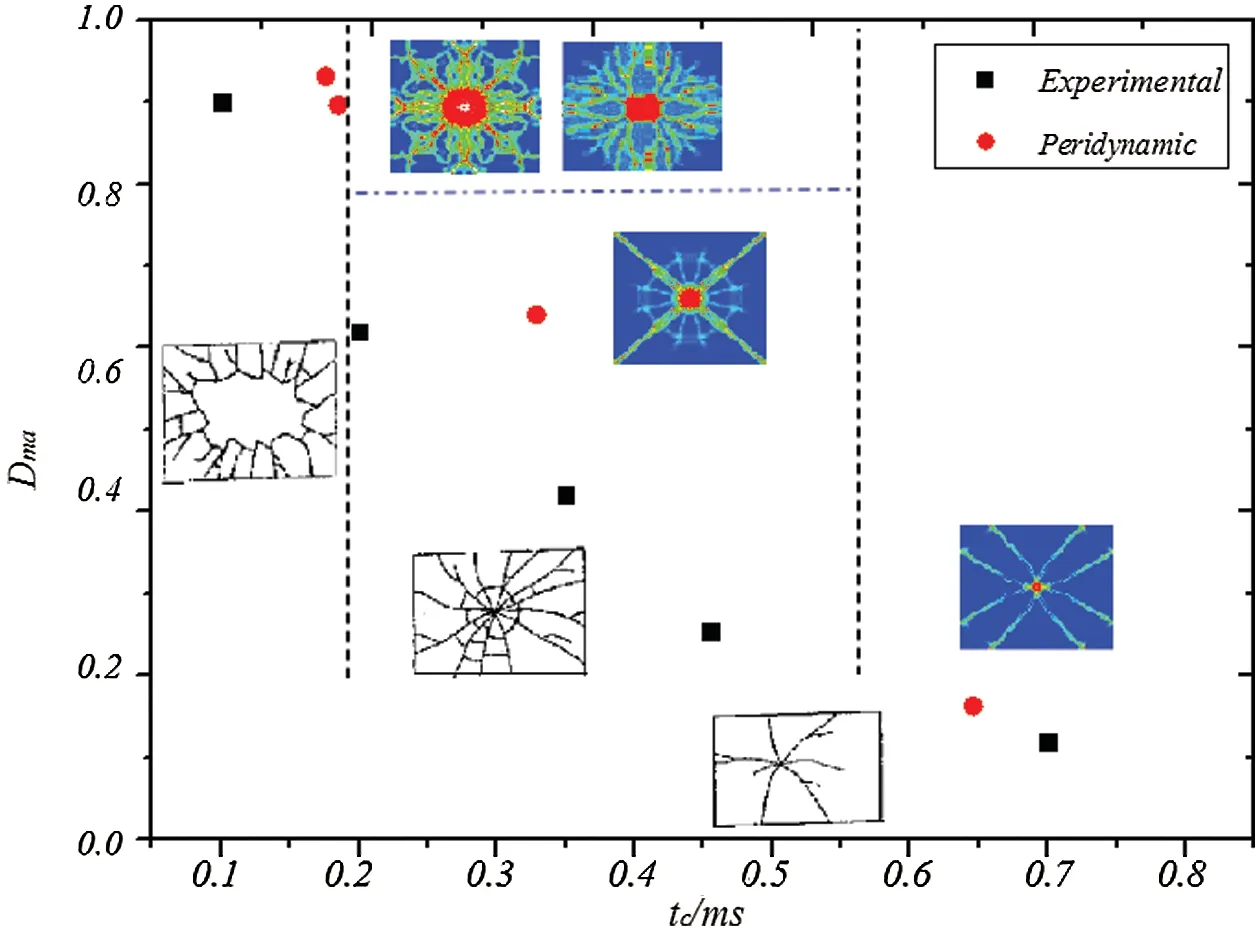
Figure 18: Damage of glass specimens at different times

5 Conclusion

This paper proposes a new contact damage model of brittle materials based on ordinary state-based peridynamic theory by introducing the contact force function.The simulation results of the Hertzian contact (nonembedded contact)problem show that the embedded distancedegradually approaches zero (the assumption of no embedding is satisfied), and contact forceFcgradually approaches the theoretical solution with the increase in contact moduluscn.Therefore,for nonembedded contact problems, the value of the contact moduluscnshould be as large as possible to satisfying the computer truncation error and the stability requirements of differential solution.The calculation error of the contact force decreases with the decrease in relative discrete size.The smaller the relative discrete size (the more discrete material points), the more time consuming the calculation.When the relative discrete size is less than a certain critical value, the effect of improving the error is unremarkable.The penalty-based method of peridynamics can be used to simulate the contact problem well by selecting the appropriate relative discrete size and the contact modulus.The low loading rate of DBT and high loading rate of SHPB are considered to simulate the failure process of glass specimen under impact load.For low loading rate, the final damage form is mainly a small amount of fragments.For the high-speed impact of SHPB, the sample appears to be broken.The simulation results are in good agreement with the test results.

The proposed damage contact model of peridynamics has a good application prospect and can be extended to the simulation of other similar materials, such as the impact fracture process of ice.The calculation model can be enriched and developed.The contact force only considers the vertical force.If the horizontal friction force is considered simultaneously, the response and failure mechanism of typical brittle materials under impact load can be better analyzed.

Acknowledgement:This research is financially by the National Natural Science Foundation of China (Nos.11932006,U1934206,12002118).And The Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No.20KJB580015).The snapshots were performed using the visualisation tool Ensight.

Funding Statement:This study was funded by National Natural Science Foundation of China(Nos.11932006, U1934206), Recipient: Qing Zhang.And National Natural Science Foundation of China (No.12002118), Recipient: Xin Gu.And Natural Science Foundation of the Jiangsu Higher Education Institutions of China (No.20KJB580015).Recipient: Runpu Li.

Conflicts of Interest:The authors claim that none of the material in the paper has been published or is under consideration for publication elsewhere.The publication has been approved by all co-authors.We have no conflict of interest to declare, All data generated or analysed during this study are included in this published article.

Appendix A.

The Herzian contact of the rigid body is considered in Fig.A-1, and the contact stress of the sphere can be expressed as

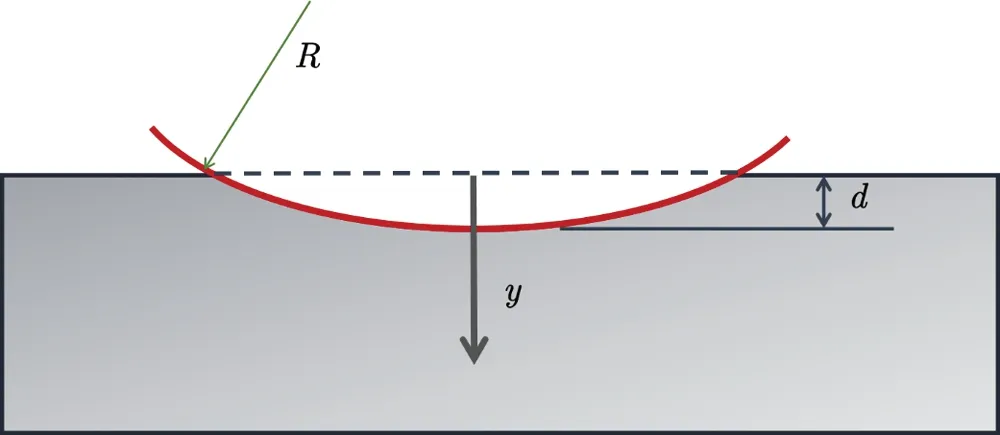
Figure A-1: Herzian contact problem of Rigid body

For a semi-infinite elastic body, the elastic mechanics solution of the concentrated forceFyis [46]

When the contact surfacey=0,

Then, when the distributed force is considered

wherer=Substituting the above Eq.(A2)into the Eq.(A4),

And

wheredis the indentation depth,Ris the radius of the sphere.The relationship between contact force and indentation depth is