基于三支决策的双激素人工胰脏模型预测控制算法研究
孙 超,孔雪华,高 军,陆凯旋,杜鹏翔
(燕山大学 河北省测试计量技术及仪器重点实验室,河北 秦皇岛 066004)
1 引 言
随着物质生活水平的提高和环境的变化,糖尿病日益成为严重危害人类健康的多发疾病。据统计,我国糖尿病患者人数达到1.144亿,已成为世界第一糖尿病大国,发病形式相当严峻。目前医学界还没有根治糖尿病的手段,胰岛素治疗是控制高血糖的重要手段,更是维持患者生命的唯一手段,人工胰脏系统被认为是治疗糖尿病最有前景的方法之一[1]。
双激素人工胰脏模拟了人体胰岛对血糖的生理调节方式,是最有希望控制血糖水平的办法。Damiano[2]提出了“双皮下注射”的理念,由模型预测控制(model predictive ontrol,MPC)和比例-积分-微分(proportional integral derivative,PID)分别控制胰岛素和胰高血糖素的注射速度[3],减少低血糖的发生; Castle[4]用两个衰减记忆比例-微分(fading memor proportional differential,FMPD)控制器分别控制胰岛素和胰高血糖素的输注速度,证明了双激素血糖调节方法的临床可行性。但上述两项研究均采用两个独立的控制器,易造成胰岛素和胰高血糖素的同时输注。基于模型预测控制(MPC)的双激素切换控制方法[5]、基于内模的PID切换控制器(IMC-PID)[6,7]和双激素人工胰脏的经济模型预测控制[8],设计了输入胰岛素、输入胰高血糖素和零输入(两种激素都不输入)3种子模式,利用博弈论确定切换律,在3种模式中切换以达到控制效果的最优,避免了两种激素同时输注的可能,但现有研究在运行效率和群体控制质量上仍有待提高。
目前,关于双激素人工胰脏子系统切换机制的研究大多存在运行效率和群体控制质量较低的问题。为了进一步提高双激素人工胰脏的控制效果和整体效率,本文在三支决策理论和模型预测控制算法的基础上,提出一种基于三支决策的双激素人工胰脏模型预测控制算法。首先,该算法采用现有的人工胰脏预测模型并对其组合方式进行了一定的改进,3个子系统的预测模型均能独立得到各自的血糖预测值,也避免了进行大量的开环响应实验; 其次,该算法以三支决策理论为依托设计3个子系统间的切换规则,提供了一种切实可行的双激素切换规则,以解决子系统切换的决策机制问题;最后利用美国弗吉尼亚大学和意大利帕多瓦大学联合开发的UVA仿真平台完成仿真,在血糖调节效果、跟踪误差、群体控制质量和算法运行效率上取得了较好的结果。
2 基于三支决策的双激素人工胰脏模型预测控制算法研究
基于三支决策的双激素人工胰脏模型预测控制算法主要有模型预测控制和三支决策两大理论基础。首先,分别建立胰岛素子系统、零输注子系统和胰高血糖素子系统的预测模型,并用ode45算法进行求解得到各自的血糖预测值;其次,设计各个子系统的目标函数,并用粒子群算法进行优化得到最优控制输入序列,选择第1项作为当前最优激素输注速率;最后,根据最优控制输入、血糖预测值和输注激素的价格因素,设计三支决策切换规则,即设计代价矩阵,分别计算切换到每个子系统面临的风险值,选择切换到风险值最小的子系统,将其激素输注速率作为双激素人工胰脏模型预测控制算法的输出。本算法提供了一种切实可行的双激素人工胰脏子系统切换机制,算法结构框图如图1所示。
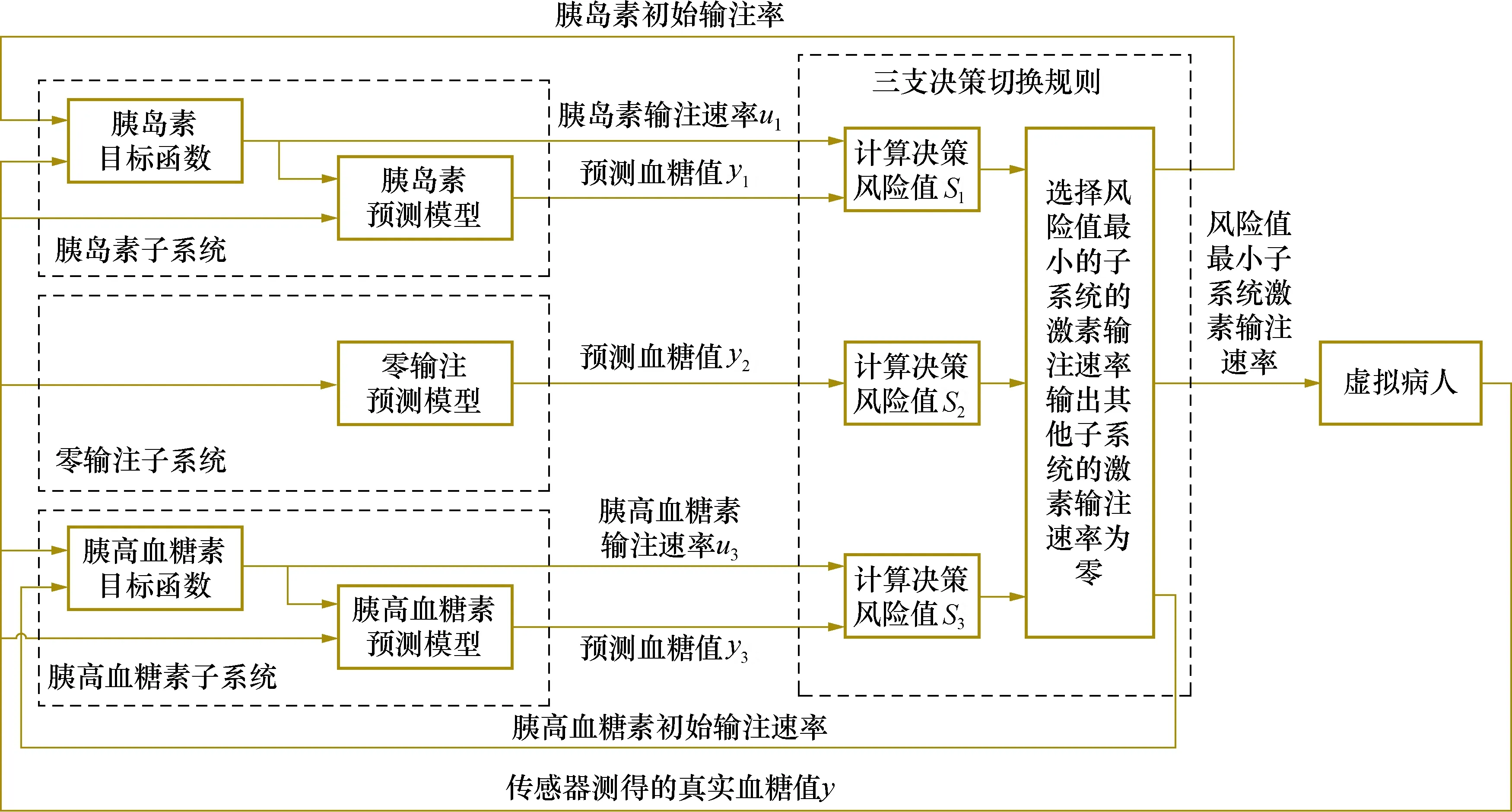
图1 基于三支决策的双激素人工胰脏模型预测控制算法结构框图Fig.1 Structural block diagram of model predictive control algorithm for double-hormone artificial pancreas based on three-branch decision theory
2.1 建立预测模型
本算法包含胰岛素子系统、零输注子系统和胰高血糖素子系统,分别建立3个子系统的预测模型并利用ode45算法求解得到各个子系统的血糖预测值。假设u1代表胰岛素输注速率;u2代表零输注子系统的输入,值恒为0;u3代表胰高血糖素输注速率;y1代表胰岛素子系统的血糖预测值;y2代表零输注子系统的血糖预测值;y3代表胰高血糖素子系统的血糖预测值。
胰岛素-血糖模型选用应用较为广泛的Bergman最小化模型[9~11]。Bergman最小化模型综合考虑了血糖的降解、胰岛素的降解、胰岛素对机体吸收血糖速率、肝糖原输出速率等因素对血糖值的影响,由3个微分方程构成的微分方程组表示,公式为:
(1)
式中:t为时间;Gb、Ib分别为基础状态下的血糖、血浆胰岛素的浓度;I(t)为血浆胰岛素浓度与其基础值的差值,μU/ml;X(t)为细胞组织间隙胰岛素浓度;P1为在基础胰岛素水平下,葡萄糖自身代谢和抑制肝糖输出的效能,min-1;P2为细胞组织间隙胰岛素自身降解系数,min-1;P3为组织中胰岛素代谢调控作用的系数,min-2·(μU/ml)-1;n为血浆胰岛素自身降解系数,min-1;V1为体积,L。
零输注子系统的模型采用改进的最小葡萄糖动力模型,公式如下:
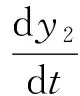
(2)
式中:t为时间;Gb为基础状态下的血糖的浓度;SG为部分葡萄糖效果,min-1。
关于胰高血糖素-血糖模型的研究相对较少,胰高血糖素子系统的预测模型是将关于胰高血糖素输注速率-血浆胰高血糖素浓度的吸收模型和关于血浆胰高血糖素浓度-血糖值的葡萄糖模型进行组合构成复合模型[12,13]得到的。该复合模型是由5个微分方程构成的微分方程组,如式(3)所示。
(3)
式中:t为时间;Nb为基础状态下的血浆胰高血糖素浓度;N(t)为血浆胰高血糖素的浓度,pg/mL;Y(t)为胰高血糖素对葡萄糖产生的作用,min-1;Z1(t)、Z2(t)为皮下注射胰高血糖素的两室吸收,pg/kg;SG为部分葡萄糖效果,min-1;SN为胰高血糖素的敏感性,min-1/(pg/dL);P4为描述胰高血糖素作用的时间常数的倒数,min-1;kN为胰高血糖素清除速率,min-1;tN为胰高血糖素吸收时间常数,min;VN为血浆胰高血糖素分布体积,mL/kg。
2.2 目标函数的设计与求解
由于零输注子系统的控制输入始终为零,因此无需设计零输注子系统的目标函数。血糖调节的目的是将血糖控制在[70,180]的区间内,为进一步提高控制效果,在区间控制的前提下进一步调节血糖使其接近设定值。由于低血糖风险远高于高血糖风险,因此取正常区间中间偏上值130 mg/dL为设定值。设计包含设定值控制和区间控制2方面的目标函数,胰岛素子系统和胰高血糖素子系统的目标函数包括控制输入、血糖预测值与设定值偏差和血糖预测值与区间偏差3部分,如式(4)和式(5)所示。

(4)
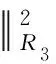
(5)
s.t. Δumin≤Δu(k+i)≤Δumax
umin≤u(k+i)≤umax, (i=0,1,…,M-1)
式中:J1、J3分别是所设计的胰岛素子系统、胰高血糖素子系统的目标函数;y1(t)、y3(t)分别表示胰岛素子系统和胰高血糖素子系统的血糖预测值;ysp(t)=130 mg/dL为血糖设定值;ΔU(t)为最优控制输入增量;u(k+i)为系统的最优控制输入;R1、R3,Q1、Q3,S1、S3分别为目标函数3部分对应的权值。
区间偏差部分是一个分段函数,当血糖预测值高于区间上限时,偏差值是血糖预测值与区间上限间的距离;当血糖预测值处于正常区间范围内时,偏差值始终为0;当血糖预测值低于区间下限时,偏差值是血糖预测值与区间下限间的距离。因此区间偏差值越小越好,与对目标函数进行最小优化一致,可作为目标函数的一部分。利用粒子群优化算法对2个目标函数进行求解得到2个子系统的最优控制输入序列,选择第1项作为当前时刻的最优输入值即胰岛素和胰高血糖素输注速率。
2.3 三支决策切换规则
利用三支决策理论进行决策,包含两个状态集和3个行动集,并根据贝叶斯准则选择期望损失最小的行动集执行。基于三支决策的双激素人工胰脏模型预测控制算法中,3种决策行动分别对应着执行胰岛素子系统、执行零输注子系统和执行胰高血糖素子系统,两个状态集为血糖预测值处于区间[180,+∞]和血糖预测值处于区间[0,180]。所设计的三支决策代价矩阵如表1所示,该矩阵由上述状态集、行动集组成,矩阵值表示在该状态下采用该行动集所付出的代价。
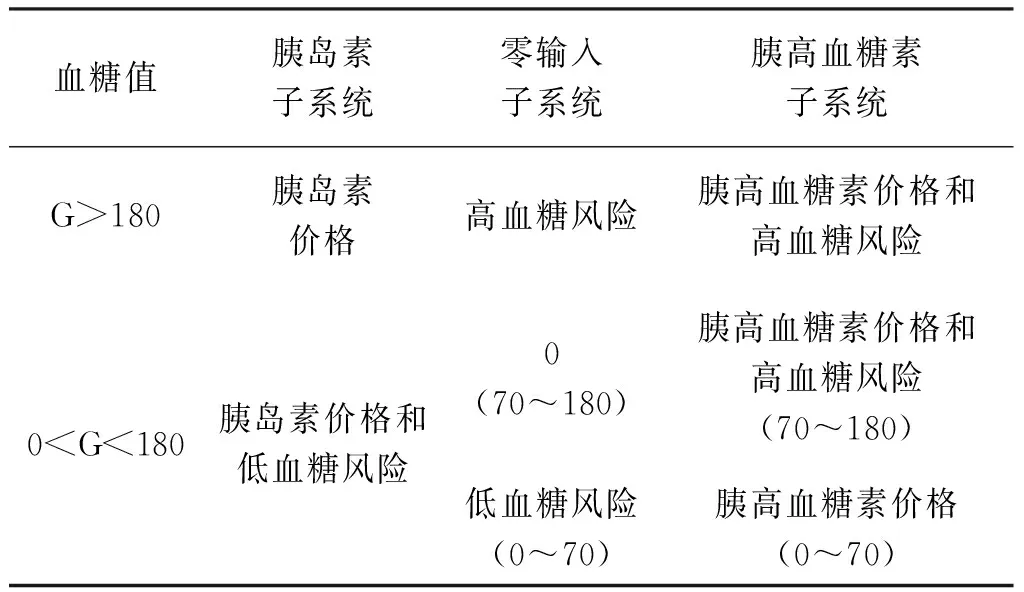
表1 双激素人工胰脏三支决策切换的代价矩阵Tab.1 The cost matrix of the three-branch decision switching of double-hormone artificial pancreas
代价矩阵中,价格因素由激素的价格和输注速率2部分构成,高低血糖风险由预测血糖与区间上下限间的偏差组成。假定在血糖预测值处于区间[180,+∞]时执行3个行动集的代价分别为λ11、λ12、λ13,在血糖预测值处于区间[0,180]时执行3个行动集的代价分别为λ21、λ22、λ23,有:

(6)
式中:y1、y2、y3分别为3个子系统的血糖预测值向量;y1i、y2i、y3i分别表示3个向量的分量;yH、yL分别表示由区间上限和区间下限组成的向量;m1、m2分别为胰岛素和胰高血糖素的价格;R2、R4分别为胰岛素和胰高血糖素经济代价的权重系数;Q2、Q4分别为高血糖风险和低血糖风险的权重系数;u1代表胰岛素输注速度向量;u3代表胰高血糖素输注速度向量。
假设血糖预测值处于[180,+∞]和[0,180]区间的概率分别为p1、p2,执行3个行动集的期望损失分别为S1、S2、S3,则有如下关系:
S1=p1λ11+p2λ21
S2=p1λ12+p2λ22
S3=p1λ13+p2λ23
(7)
由于只有2个状态集,p1+p2=1,式(7)可转化为:
S1=λ21+p1(λ11-λ21)
S2=λ22+p1(λ12-λ22)
S3=λ23+p1(λ13-λ23)
(8)
根据贝叶斯准则可知,当S1≤S2且S1≤S3时,执行胰岛素子系统;当S2≤S1且S2≤S3时,执行零输入子系统;当S3≤S1且S3≤S2时,执行胰高血糖素子系统。结合式(8)可知,选择执行胰岛素子系统等价于式(9)成立。
λ21+p1(λ11-λ21)≤λ22+p1(λ12-λ22)
λ21+p1(λ11-λ21)≤λ23+p1(λ13-λ23)
(9)
血糖预测值处于[180,+∞]时执行胰岛素子系统是正确决策,血糖预测值处于[0,180]时执行胰岛素子系统是错误决策。实际进行决策时正确决策的代价应小于延迟决策的代价,延迟决策的代价应小于错误决策的代价,因此有λ11≤λ12≤λ13和λ23≤λ21且λ22≤λ21,则式(9)可转化为:
(10)
综上可知,选择执行胰岛素子系统等价于式(10)成立。同理可得,选择执行零输注子系统等价于式(11)成立,选择执行胰高血糖素子系统等价于式(12)成立。
(11)
(12)
令α=(λ22-λ21)/(λ11-λ21-λ12+λ22),β=(λ22-λ23)/(λ22-λ23-λ12+λ13)可知,三支决策理论选择执行期望损失最小的行动集的规则等价于:当p1≥α时执行胰岛素子系统;当β≤p1≤α时执行零输注子系统;当p1≤β时,执行胰高血糖素子系统[14]。
设计三支决策切换规则有2种方法,一是根据设计的代价矩阵直接计算选择执行3个子系统的决策风险值,切换到风险最小的子系统;二是根据设计的代价矩阵值计算阈值α、β,并与血糖预测值处于区间[180,+∞]的概率进行比较,决策切换到相应的子系统。
2.4 粒子群算法求解目标函数
本文算法中通过优化胰岛素子系统和胰高血糖素子系统的目标函数得到当前最优的控制输入即激素输注速率,采用粒子群优化算法求解目标函数[15,16]包括如下步骤:
步骤1:对如式(4)、式(5)所示的目标函数的参数、初值和粒子速度进行初始化设置。
步骤2:根据初始化值计算设计的目标函数值。
步骤3:计算个体极值和群体极值,个体极值是每个潜在解移动过程中使目标函数值最小时的输注速率值,群体极值是所有潜在解所搜索到的使目标函数值最小时的输注速率值。
步骤4:利用式(13)更新个体速度和位置。
(13)

步骤5:更新目标函数值,根据更新的粒子速度和位置计算相应的目标函数值。
步骤6:更新个体极值和群体极值,根据更新的目标函数值,从中选出最小值对应的激素输注速率即为个体极值和群体极值。
步骤7:将迭代次数设为终止条件,若已达到所设置的最大迭代次数,输出最优解;否则,转第4步,寻找下一个最优解。
3 仿真结果分析
为验证本文所提算法的可行性及有效性,采用美国弗吉尼亚大学和意大利帕多瓦大学联合开发的UVA仿真平台进行仿真实验[17]。该平台提供了33个虚拟病人,其中11个成人、11个青少年和11个儿童,基本涵盖了各个年龄段的糖尿病患者。选择33个虚拟病人,设计分别在早上7:00,中午12:00和下午18:00摄入45 g、70 g和80 g的碳水化合物的场景,取预测步数为24,控制步数为10进行为期一天的仿真实验。实验中设置初始血糖值为100 mg/dL,设置体现个体差异性的胰岛素基础输注速率,控制目标是将血糖调节到[70,180]的区间内,胰岛素价格设为0.3元/U,胰高血糖素价格为 1元/U[8]。
对于仿真结果分别从个体和整体2部分进行分析,从33个实验对象中选择1个个体对其结果进行分析,该个体的血糖曲线、对应的胰岛素输注速率曲线和胰高血糖素输注速率曲线如图2所示。其中,图2(a)是该个体在控制过程中血糖浓度随时间变化的曲线,图2(b)是控制过程中胰岛素输注速率随时间变化的曲线,图2(c)是控制过程中胰高血糖素输注速率随时间变化的曲线。对3个子图分析得到3个子系统的工作时间分布如图3所示,其中采用胰岛素子系统输出值为1,采用零输注子系统输出值为2,采用胰高血糖素子系统输出值为3。

图2 基于三支决策切换规则的人工胰脏个体控制效果图Fig.2 Artificial pancreas individual control effect based on three decision switching rules

图3 3个子系统工作时间分布图Fig.3 Working time distribution of the three subsystems
实验过程中设置该个体的胰岛素基础输注速率为55.475 6 pmol/min,从图2(a)可以看出,该个体的血糖值始终处于[70,180]的正常范围内,在设定值130 mg/dL附近上下浮动;虚拟病人分别在420 min、720 min和1 080 min时用餐,并且血糖随之升高。综合分析图2可知,在0 min时虚拟病人经过长时间的睡眠,血糖水平下降,因此输注胰高血糖素以维持血糖,185 min后血糖逐渐升高,停止输注胰高血糖素。420 min时病人用餐,血糖大幅度升高但可依靠胰岛素基础输注速率将血糖控制在正常范围内,因此无需输注大剂量胰岛素,胰岛素子系统不工作。随着餐后血糖不断被消耗利用,497 min时血糖开始下降,693 min时血糖低于设定值,输注胰高血糖素减缓血糖下降速率。720 min时病人再次用餐,血糖不断升高,782 min时血糖高于区间上限,输注大剂量胰岛素,801 min时血糖恢复到正常区间内,胰岛素子系统停止工作。1 025 min时血糖低于设定值,输注胰高血糖素减缓血糖下降。1 080 min时病人再次用餐,血糖升高,1 142 min时输注大剂量胰岛素,1 161 min时血糖恢复到正常区间内,胰岛素子系统停止工作。综上所述,本文算法将该个体的血糖浓度控制在正常范围内,且没有低血糖事件的发生,获得了较好的控制效果。
从图3可以看出,在782~801 min和1 142~ 1 161 min时,胰岛素子系统工作,进行大剂量胰岛素的输注;在0~185 min、361~448 min、693~765 min和1 025~1 117 min时,胰高血糖素子系统工作,为虚拟病人输注胰高血糖素;其余时间即为零输注子系统的工作时间。
对33个虚拟病人进行仿真实验,实验对象血糖值随时间变化的曲线如图4所示,反映33个虚拟病人整体的血糖平均状态及最值的血糖跟踪图如图5所示,血糖密度图如图6所示,控制变异性网格分析(CVGA)如图7所示。
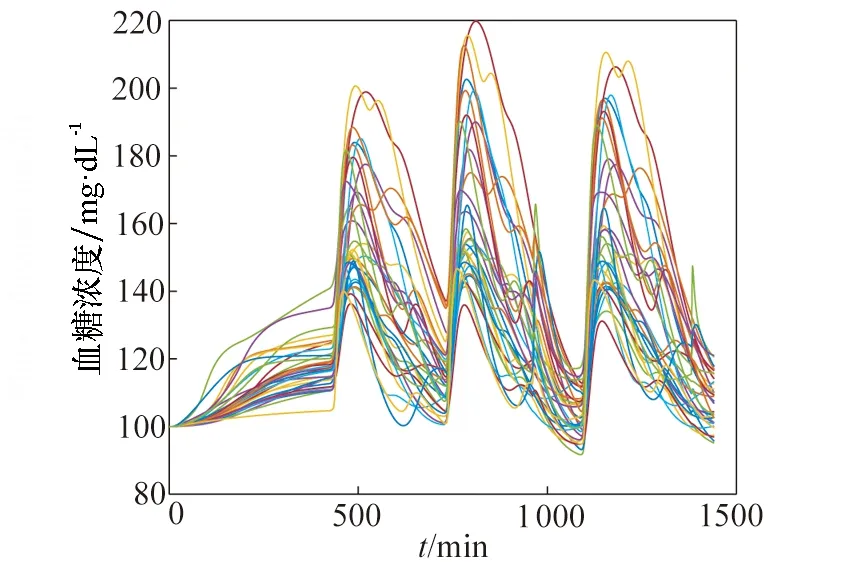
图4 33个虚拟病人的血糖浓度曲线Fig.4 Blood glucose concentration curves of 33 virtual patients
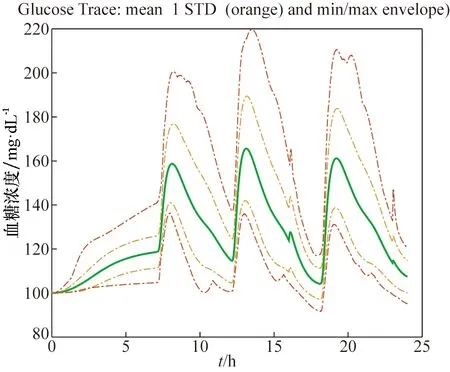
图5 血糖跟踪轨迹曲线Fig.5 Trace curve of blood glucose
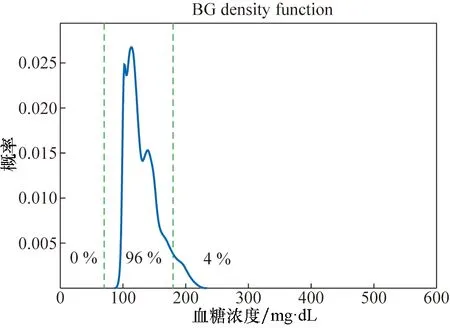
图6 血糖密度图Fig.6 Blood glucose density
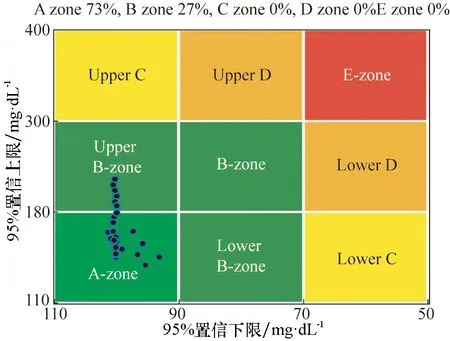
图7 控制变异性网格分析图Fig.7 Schematic diagram of Control-Variability Grid Analysis
从图4可看出,除个别对象出现短时间轻微高血糖现象外,绝大部分虚拟病人的血糖处于正常范围内,得到了良好的控制效果。图5中绿色曲线表示33位虚拟病人的平均血糖状态,仿真过程中始终处于正常血糖范围内;红色曲线分别表示33位虚拟病人血糖水平的最值情况,可看出仅有最大值存在轻微高血糖现象。图6血糖密度图给出了血糖的概率分布,可看出33个虚拟病人全部血糖值中只有4%处于轻微高血糖,96%均处于正常范围内,无低血糖状况。图7中横、纵坐标均为血糖值,处于A区域为较好结果,可看出33个虚拟病人中,73%处于A区域,27%处于B区域,取得了较好的控制效果。现有研究的控制变异性网格分析结果为40%处于A区域,60%处于B区域[5,6]或100%处于B区域[8],因此本算法在群体控制质量上有着显著提高。此外,该算法运行时间为526 s,具有较高的运行效率。综合分析图4、图5、图6和图7,本算法在33位虚拟病人身上取得了良好的控制效果。
最后,33位虚拟病人的血糖指数和血糖标准差数据如表2所示,主要包括血糖均值、低血糖时间百分比、正常血糖时间百分比、高血糖时间百分比、血糖指数(BGRI)和血糖标准差数据(RoC)。血糖指数值和血糖标准差越小,风险就越小,表格中BGRI最大为4.67,RoC最大为0.93,可看出基于三支决策的双激素人工胰脏模型预测控制算法的风险很低,具有较高的安全性。
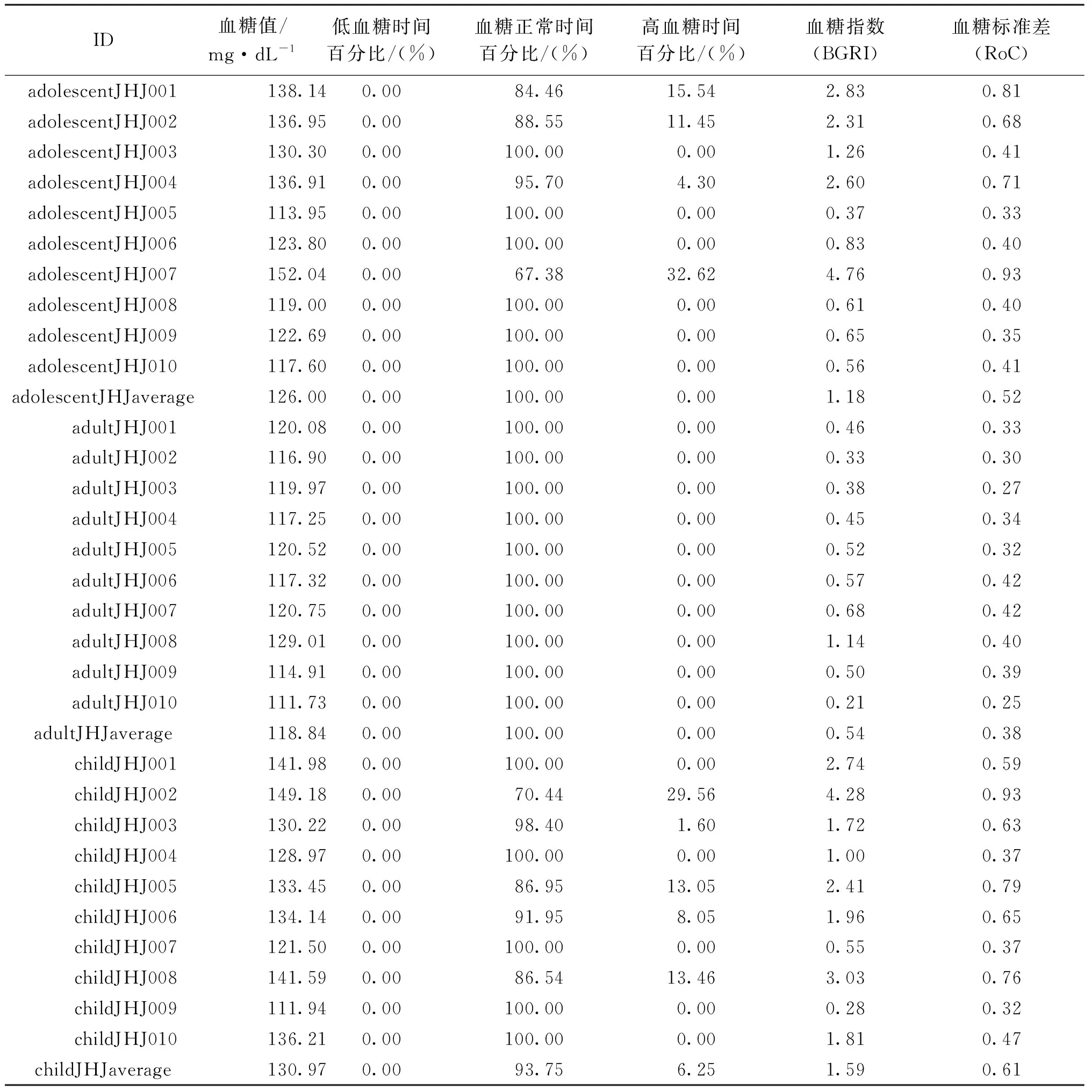
表2 血糖指数和血糖标准差分析Tab.2 Analysis of glucose index and glucose standard deviation
4 结 论
针对双激素人工胰脏子系统切换决策机制研究较少且存在运算效率和群体控制质量有待提高的问题,本文提出一种基于三支决策的双激素人工胰脏模型预测控制算法。该算法综合考虑了控制效果和经济代价2个方面因素设计了三支决策切换规则,在现有的人工胰脏预测模型基础上,设计了包含设定值控制和区间控制两部分的目标函数,并用粒子群算法求解。最后对33位虚拟病人进行仿真实验,从血糖曲线、激素输注速率曲线、血糖跟踪图、血糖密度图、控制变异性网格分析、血糖指数和血糖标准差多个方面对控制效果进行分析,证明该算法能很好地将血糖控制在正常范围内,在跟踪误差、风险指数和运行效率上取得了良好的效果,在对多个病人的群体控制质量上有显著提高。

