基于目标层级分析法的复杂重型装备顶层任务分解
刘 颖,董浩然,王富强,焦喜振
(1.重庆大学 机械与运载工程学院,重庆 400044; 2.中国重型机械研究院股份公司,陕西 西安 710032)
0 前言
复杂重型装备是我国制造产业链中的关键基础装备,标志着国家的制造能力与制造水平,对我国的经济发展与国防安全具有重要作用。复杂重型装备不同于其他普通装备,其一般用于核电、化工和国防等特定领域,具有规格大、结构复杂、个性化定制程度高、研制周期长等特点[1]。复杂重型装备的研制过程涉及了大量不同领域的知识和行业资源,往往要通过多家企业协同完成。因此,有必要对复杂重型装备研制初期总体任务进行合理分解,从而提高资源的利用效率和缩短研制周期。
在任务分解方面,已有大量学者对此进行研究。庞辉[2]等借用了软件度量的思想,建立了任务内聚系数的计算公式,同时提出了一种基于项目、任务和活动的定性任务分解策略。包北方[3]等综合考虑任务粒度、耦合度和均衡度等因素,提出一种基于定量分析的任务分解系统模型,从而对定制产品协同开发过程中的资源进行合理配置并缩短了开发周期。刘明周[4]等对云制造环境下的任务模型和任务约束结构进行描述,采用基于分层任务网络的递归分解算法,解决了多层次、多粒度的任务分解与资源匹配问题。刘建刚[5]等首先采用设计结构矩阵对产品结构进行建模,然后通过遗传算法实现了对产品结构模型的智能化分解聚类。Dan[6]对任务属性与源任务间的关系进行了研究,基于公理化设计矩阵建立模型并给出任务分解的一般流程。石培文[7]利用WBS结构和任务相关度矩阵等方法对任务粒度和耦合度进行分析,并建立设计任务分解方法一般模型。栾兆东[8]提出一种考虑结构-工艺两模块协同分解过程,并且通过映射的方式构建了输入输出模型,最终得到任务总分解结构以及任务细化分解结构。上述研究成果大部分从粒度较细的任务(如组件级和部件级任务)的角度出发,探究这些任务之间的交互关系并提出相应的任务分解方法,鲜有对总体任务与系统及任务进行研究。同时这些方法的应用领域为结构较为简单的普通设备,可能不适用于结构复杂的个性化定制类复杂重型装备的任务分解。
基于此,本文对复杂重型装备的顶层任务分解问题进行研究。将目标层级分析法引入顶层任务分解过程中,分析了顶层系统与分系统之间的信息传递,构建了复杂重型装备顶层目标分析模型和分系统级目标分析模型,并通过实例对模型的有效性进行验证。
1 目标层级分析法概述
目标层级分析法(Analytical Target Cascading,ATC)最初是由Kim等人在研究复杂工程优化问题时提出[9]。目标层级分析法是多学科设计优化方法的分支,采用并行思想来解决复杂系统的设计方法。结合传统的多学科设计优化方法(如两级集成系统综合法、协同优化理论等)及分解协调策略,基于模型的物理结构、生产流程等属性对系统逐层分析。ATC现已在汽车底盘和飞行器的设计中得到应用[9-10]。
目前在解决大型复杂问题的优化设计方法中,传统的多学科综合优化方法采用单分析模型对整个设计问题进行控制,其效率和可行性均不尽如人意;为了提高优化模型的可行性,部分学者提出了层级框架理论,在降低了模型复杂度的同时也牺牲了系统优化的协同性,导致分析模型的失真,实用性较差。针对这一情况产生的协同优化方法,虽然增加了联系变量和各分支间的藕合信息,但其前提是假定分解后的分析模型处于同一层次,相互间的关联较为密切,对问题的分解要求比较严格,稍有不慎,其收敛性以及收敛效率均很难保证,在实际应用中普及难度较大。
目标层级分析法正是结合层级优化框架和协同优化理论的优势,将设计问题逐层分解,形成经严格定义的优化问题的层级式集合。通过保证层级间目标传递偏差的最小化,获得系统内部的兼容性和自适应性,其优点如下:
(1)降低了分析模型的失真程度,具有较好的实用性和可行性。
(2)将目标的传递过程和匹配过程集成到一个单一的进程中,大幅降低了整个设计的迭代次数。
(3)允许子级优化问题采用并发式设计,根据需要对现有的优化设计方法加以利用,具有较高的灵活性,其优越的收敛特性及收敛效率也已经得到证明。
(4)将设计规划问题分解为系统、分系统、子系统和组件等元素构成的有机集合,降低了整个设计问题的复杂性。
2 复杂重型装备系统的顶层任务分解
2.1 基于目标层级分析法的顶层任务分解
目标层级分析法是按目标分解系统的多层分级优化设计方法,其目标的分解流程如图1所示。在此方法中,总任务按照层级分解到子任务,子系统可继续分解,每一层级作为一个子系统,每个子系统有且仅有一个上一级的父系统,但可有多个下一级的子系统,如图2所示。每个子系统包含分析模型和优化模型,且同时接受上一层级父系统的分析信息和下一层级子系统的反馈信息,并且在分解的过程中将这些信息作为参数。该层级子系统的优化结果作为目标值下发给下一层级的子系统,同时作为性能函数的输出反馈到上一层级的父系统。当各层级父系统、子系统之间的输入输出偏差符合要求时停止迭代。该方法是一种自上而下又从下而上反复迭代修正的过程,层级分解过程中遵循任务分解原则,使得各子系统能并行处理,提高任务的执行效率。

图1 目标层分解过程
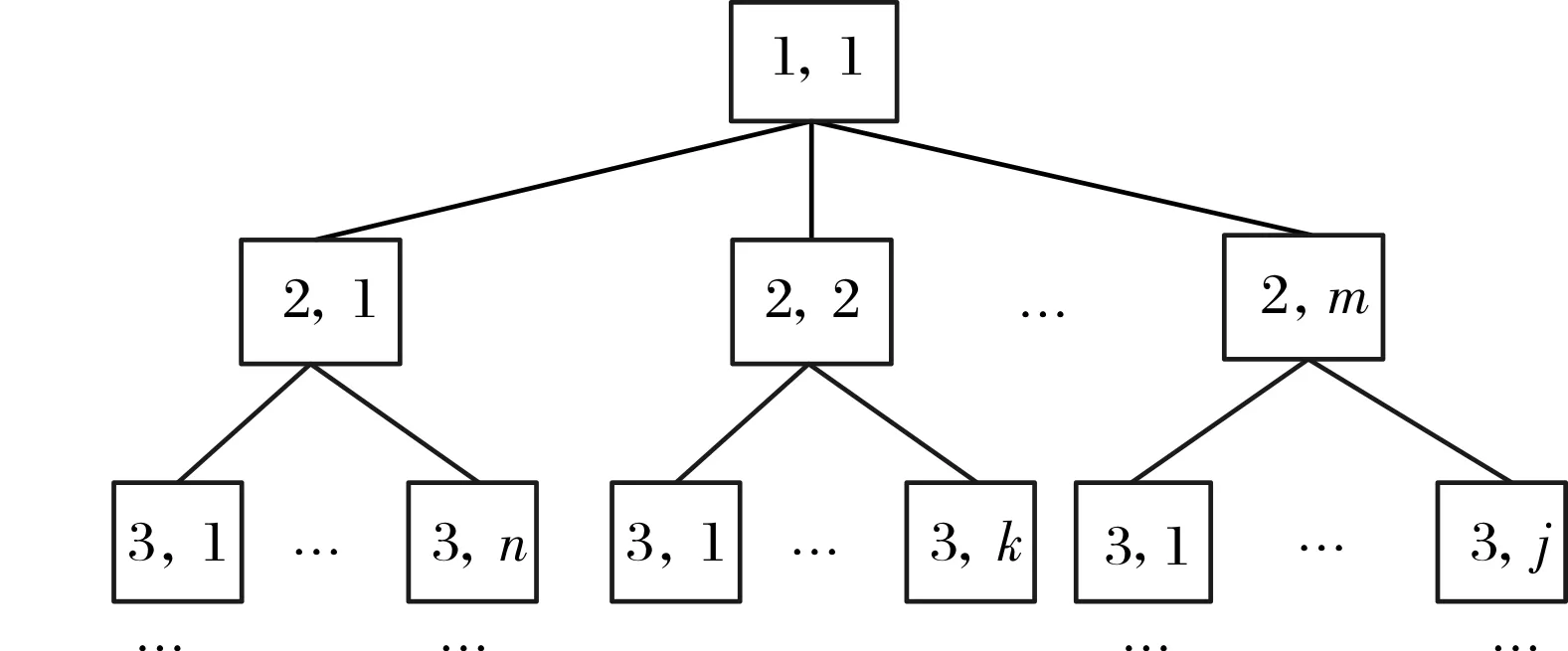
图2 多层分级系统结构
在目标层级分析法这类模型中,顶层任务为单独一个模块,其他层次都被分为若干个子系统,每个子系统由两类不同的模块组成,分别为优化模块T、分析模块r(如图3)。分析模块是以变量、参数和子系统之间的反馈作为其输入,通过计算分析模块的反馈值,输出并传递其相应的优化设计模块。优化设计模块则是利用分析模块计算出各层子系统问题的反馈。如果同层级的多个模块共享变量,那么将变量成为联系变量。

图3 各层级信息传递交互
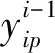
目标层级分析顶层系统优化模型如下:
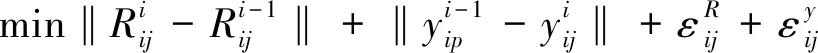
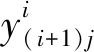
若Tij无子系统,那么其目标函数就不包含ε,如底层系统。若某一层系统无联系变量,那么其目标函数中就无联系变量项和用于协调联系变量所设定的偏差容限,如顶层系统。
2.2 复杂重型装备系统顶层分解分析模型
本文主要以复杂重型装备双层分解系统为例,研究目标层级分析法在复杂系统中任务分解的优化过程。如图4所示,顶层为总任务,下层为分系统级任务。目标层级分析法可延伸到多层级复杂系统分级优化,若系统较为复杂,可进行多层级优化分级设计。对于复杂重型装备产品的研制,需要多家企业、多个子单位协作共同完成,在复杂重型装备产品的顶层任务分解过程中需要对其分层降解,根据结构、功能等进行初次分解后,同时保证子系统之间有较强的独立性。另外由于复杂重型装备分系统级服务的有限性,在分解过程中,需要考虑对各资源的历史评价,以满足客户对其产品的要求,一般要求包括成本、质量、工期、历史客户满意度、综合能力、信任度和历史合作关系等,因此构建模型时需要考虑以上约束对其进行任务分解,最终才能得到合理的分解结果。

图4 顶层系统和各分系统信息传递过程
对于总任务T,下级分为N个子系统,顶层任务的目标为最大程度满足客户各项指标要求(成本、质量、工期、历史客户满意度、信任度、历史合作关系、综合能力)的前提下进行任务分解,各企业每完成一次协同项目,平台都会有相应指标的历史记录,通过对指标的要求进行合作伙伴的选择;顶层系统将目标进行分层降解传给分系统层,分系统层同样要满足以上客户要求的各项指标;同时分系统级根据自身情况将实际指标反馈给顶层系统,判断总任务指标是否符合要求,若不符合则重新协调分配直到满足各项指标要求为止。
(1)参数及变量表示。C0为顶层系统的成本;CPj为分系统j的成本;Q0为顶层系统的质量;QPj为分系统的质量;D0为顶层系统的工期;DPj为分系统的工期;B0为顶层系统对企业信任度要求;BPj为分系统对企业信任度要求(客户、供应链等多角色对其的综合信任度);W0为顶层系统对企业的历史合作关系要求;WPj为分系统对企业的历史合作关系要求;S0为顶层系统对企业的历史客户满意度要求;SPj为分系统j对企业历史客户满意度要求;I0为顶层系统对企业的综合能力要求;Ipj为分系统j对企业的综合能力要求(包括产品研制能力、供货能力等等)。
(2)顶层系统目标分析模型。顶层系统要解决的问题:在满足局部变量约束和分系统反应偏差容限约束的条件下,使顶层系统反应T对目标的偏差最小。

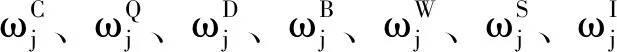
(3)分系统级目标分析模型。分系统级要解决的问题是在满足局部变量约束的条件下,使分系统反馈对顶层设定的反馈目标的偏差最小化。分系统级目标分析模型:
w.r.t.CPj,QPj,DPj,BPj,WPj,SPj,IPj
CPj,QPj,DPj,BPj,WPj,SPj,IPj≥0

3 案例分析
以125 MN双动铝挤压机的制造任务为例,对本文提出的复杂重型装备的顶层任务分解方法进行应用。125 MN双动铝挤压机是典型的复杂重型装备,其体积庞大、结构复杂,由多个不同的系统模块组成,包括主工作缸系统、挤压系统、主剪刀系统、移动模架及快换装置系统、润滑装置系统、控制平台等,组成的零部件数量众多。125 MN双动铝挤压机的结构如图5所示。

图5 125 MN双动铝挤压机结构示意图
在完成挤压机设计任务后,为了其制造任务的顺利完成和制造资源的合理选择,需要将挤压机的复杂制造任务进行合理分解,并分给不同的制造企业以协作完成,从而降低总体制造任务的复杂性和提高其研制效率。
根据提出的分解模型,对125 MN双动铝挤压机的制造任务进行顶层分解。
(1)步骤1。根据挤压机的结构和功能特性,对挤压机的总体制造任务进行分解层次规划。其分解层次结构如图6所示。
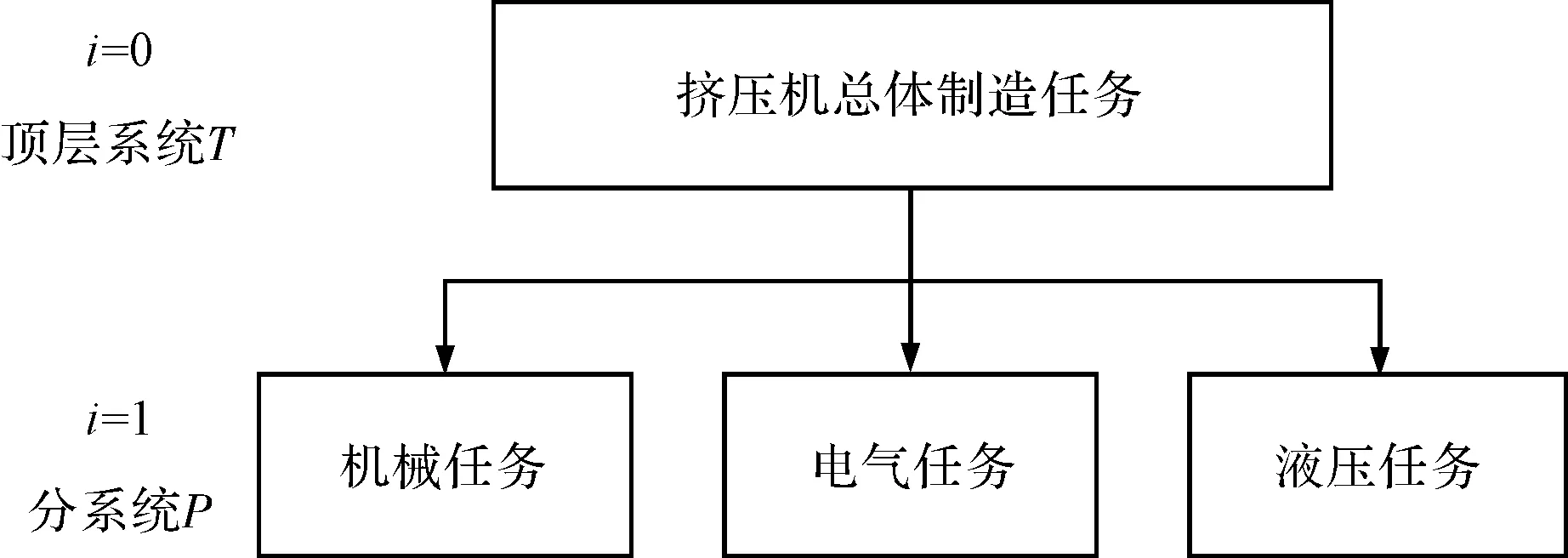
图6 挤压机顶层分解层次结构
在图6中,挤压机的总体制造任务作为顶层系统,而机械任务、电气任务和液压任务作为其下属的分系统。
(2)步骤2。参数设置。顶层系统参数:挤压机制造的各项指标参数如表1所示。
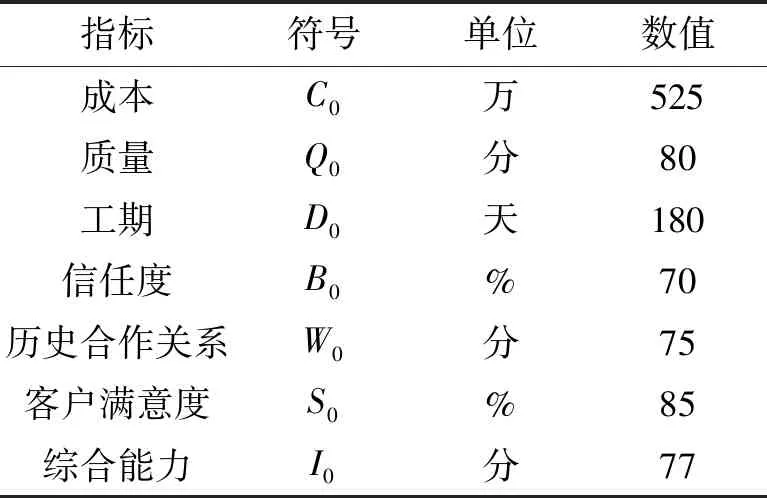
表1 挤压机的指标参数
候选企业参数:对可以完成分系统层中不同类任务的候选企业的资质进行调查,包括三家机械企业、三家电气企业和两家液压企业。其对应的指标如表2所示。
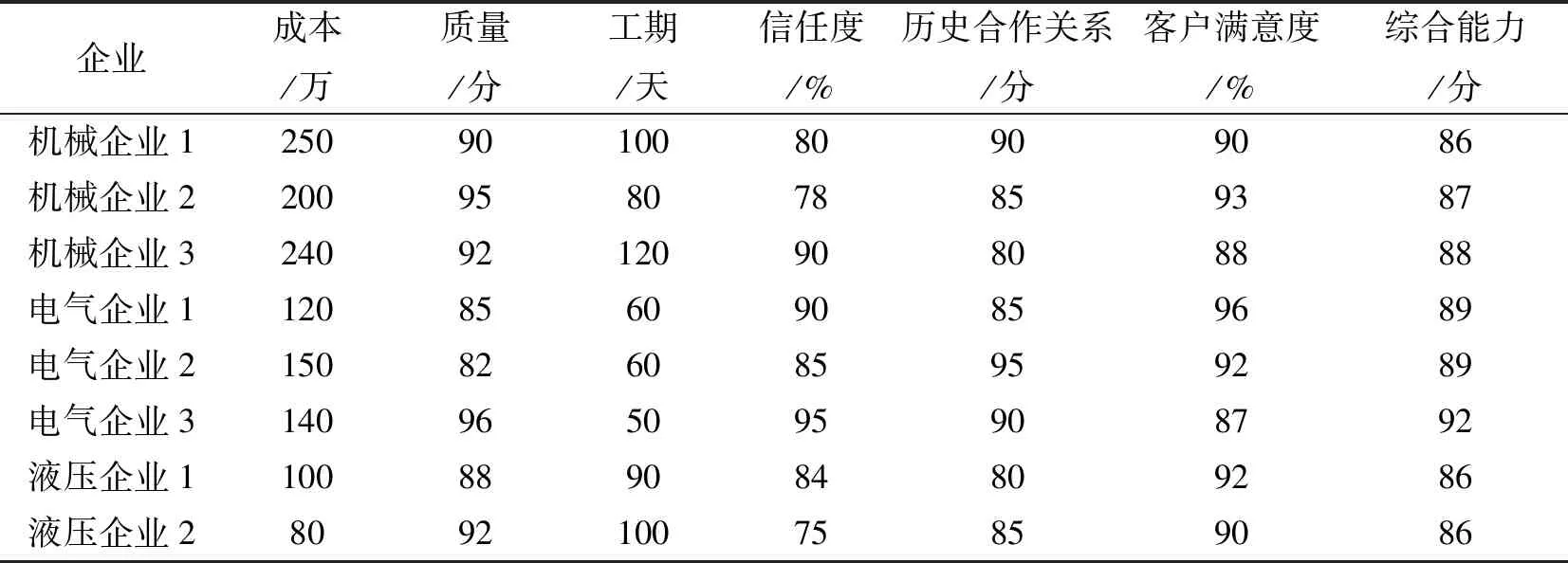
表2 企业相关指标
偏差权重。根据顶层任务分解的要求和挤压机制造任务的实际分解情况,对偏差权重进行设定,如表3所示。
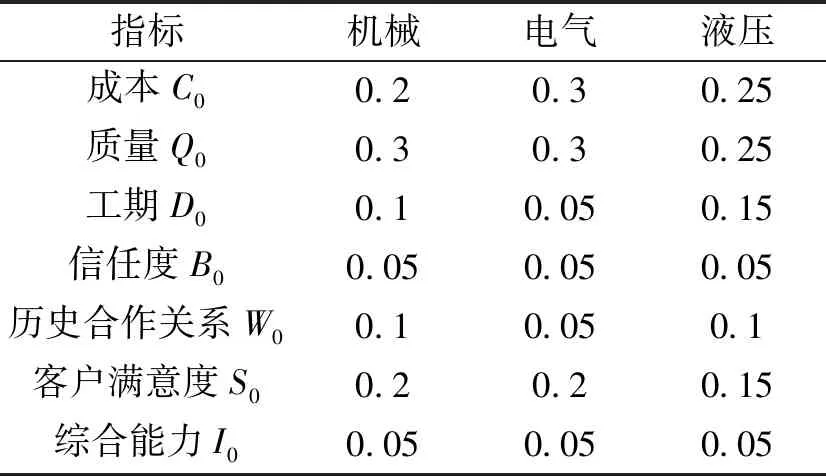
表3 系统偏差权重
(3)步骤3。将步骤2中得到的参数数据带入复杂重型装备系统顶层分解模型中,结合文献[11]和挤压机制造的实际情况,将目标偏差容限的值设置为0.02。应用MATLAB编程对模型进行求解计。顶层系统目标分析模型的目标函数如图7所示。
如图7所示,当选择分解组合2,即(机械企业1,电气企业1,液压企业2)时,顶层系统目标分析模型的目标值函数达到最小。因此,选择制造企业1承担制造任务、电气企业1承担电气任务、液压企业2承担液压任务能够使得挤压机总体复杂制造任务得到合理分解。
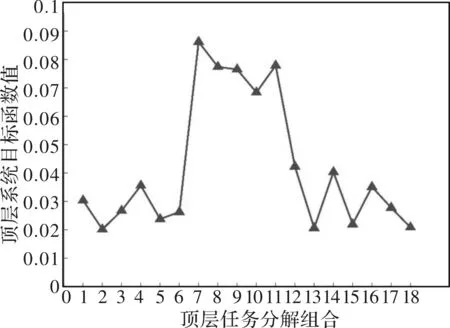
图7 顶层分解结果图
4 结论
针对复杂重型装备初期分解时总体任务所具有的复杂性,本文提出一种基于目标层级分析法的复杂重型装备顶层任务分解方法。该方法将目标层级分析法引入复杂重型装备顶层分解的过程中,分析了复杂重型装备总系统顶层任务分解到分系统级任务的过程,结合复杂重型装备总体任务分解时需要考虑的各项指标要求,分别构建了顶层系统目标分析模型和分系统级目标分析模型。最后以125 MN双动铝挤压机为例对任务分解模型的有效性进行验证。

