Multiple scattering and modeling of laser in fog∗

Ji-Yu Xue(薛积禹) Yun-Hua Cao(曹运华) Zhen-Sen Wu(吴振森) Jie Chen(陈杰)Yan-Hui Li(李艳辉) Geng Zhang(张耿) Kai Yang(杨凯) and Ruo-Ting Gao(高若婷)

1School of Physics and Optoelectronic Engineering,Xidian University,Xi’an 710071,China

2School of Environment and Safety Engineering,North University of China,Taiyuan 030000,China

Keywords: Mie theory,Monte Carlo method,engineering model,multiple scattering,error analysis

1. Introduction

Fog is a common natural phenomenon. It can reduce visibility and affect the transmission of electromagnetic waves,thus seriously influences our production and life. Studying the scattering and attenuation characteristics of lasers in fog,one can effectively analyze the environmental noise in terms of target recognition,and can set the transmission power efficiently in terms of signal transmission, which is of great significance for precisely guiding the laser weapons and signal transmission.[1]

In order to enable rapid application of attenuation and scattering models in battlefields and communication,more and more scholars devoted much effort to establishing appropriate engineering models. Yanget al.[2]compared the calculation results from the Mie theory with the results from the empirical model of attenuation and found that it is more appropriate to use the Mie theory to predict the attenuation of haze particles in the stratospheric atmosphere in the near-infrared band.Wang and Gao[3]proposed an empirical model which covers the information such as measuring distance and receiving angle of view,derived the relationship between laser attenuation coefficient and visibility in foggy weather, and presented a method of measuring distance and receiver angle of view and a new empirical formula for other information. Liet al.,[4]proposed a fog attenuation engineering calculation model by taking into account the electromagnetic wave frequency,temperature, emission angle and other parameters. This model has few input parameters and is easy to calculate. Especially the attenuation when the incident frequency is greater than

50 GHz is considered. Wu Z S and Wu T[5]calculated and analyzed the backscattering rates and transmission attenuation of two lasers(1.06µm,10.6µm)in the fog under low visibility, provided a simple statistical empirical model, and found that the 10.6-µm wavelength laser penetrates strong permeability;the smaller the visibility,the faster the laser will decay to a stable transmittance. Zhanget al.[6]established a Gaussian beam model and verified it by using Monte Carlo method.Zhonget al.[7]established and analyzed the attenuation formulas of five wavelengths. Liet al.[8]proposed a radar ranging model in a fog environment after analyzing the relationship among visibility, electromagnetic waves, and reflectivity in a fog environment. Zhaoet al.[9]considered the antenna radiation noise and characteristic of temperature increasing in the constructed radar detection range model under the influence of fog attenuation. Shahet al.[10]considered the problem of the last mile of optical communication in free space and used visibility as a measurement index. They established an engineering model for laser transmission in the fog,and compared it with other models,and analyzed the difference in parameter between models.

At present, the main methods of calculating the scattering and attenuation characteristics of fog are based on the radiation transmission theory. The particle nature of photons is used by the Monte Carlo method, finite element method,and discrete coordinate method. These methods are mainly achieved through a large number of numerical calculations or physical simulations. On the one hand, if you want to obtain accurate calculation results, it is inevitable to spend a lot of calculation time. On the other hand, for most aerosols, the main characteristics that affect attenuation and scattering are due to visibility. At the same time, in laser guidance and lidar detection,the calculation speed and response speed are the main factors influencing the military applications, so it is urgently needed to establish an engineering model for the rapid calculation and carry out related research. Therefore, on the basis of previous research, in this paper Monte Carlo method is used to calculate the laser attenuation and scattering characteristics in low-visibility fog, and the attenuation model with various laser transmission in fog is compared with the Monte Carlo method. For the incidences of laser beams with several typical wavelengths,an attenuation model under low visibility is proposed.Finally,for several types of typical lasers incident on different fogs with different visibilities, a backscattering model is established, and the error between the fitting results and the calculation results is analyzed.

2. Size distribution of fog

Fog is a colloidal system consisting of slowly sinking water droplets and ice crystals suspended in near-ground air.[11]According to the weather conditions forming fog, fog can be divided into radiation fog, advection fog, frontal fog, and mixed fog. The advection fog is the fog formed when the warm air moves to the cold underlying surface. The sea fog is usually advection fog. Radiation fog is mainly caused by ground radiation cooling,inland fog is usually radiation fog.

The droplet of fog size changes with time and space. The spherical particles that make up of the droplets of fog are mostly ice crystals and small water droplets. The distribution of these particles is uneven,but overall they can have a certain size distribution. Although the spatial and temporal change of the cloud spectrum distribution vary greatly, they can all be expressed by various distributions,among which most used is the Gamma distribution[12]

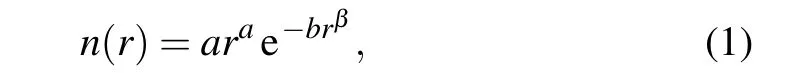
wherenrepresents the number of fog droplets within the interval of unit volume and unit radius,rdenotes the radius of fog droplet, generally the effective radius,Wrefers to the water content,Vis the visibility and its value is determined by the size distribution of the mist.

Using the empirical relationship between the advection fog water content and visibility,we can obtain the relationship between the advection fog droplet size distribution and visibility or water content as follows:

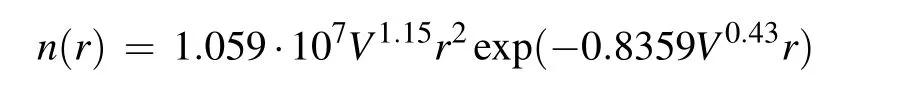
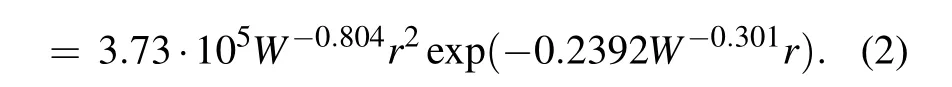
Similarly, the relationship between the droplet size distribution of the radiation fog and the visibility or water content is obtained and written below:

From Fig. 1, it can be seen that, generally speaking, the size distribution at the wavelengths of 0.86 µm, 1.06 µm, and 1.315µm vary substantially with the visibility,while the size distribution at the wavelength of 10.6µm changes drastically,and under the same visibility, the size is much smaller than those at the remaining wavelengths. The sizes at these wavelengths in the radiation fog are also larger than that of the advection fog under the same visibility.

Fig. 1. Variation of advection fog and radiation fog size distribution with visibility: (a)advection fog,(b)radiation fog.

3. Laser attenuation and scattering characteristics in fog

3.1. Mie theory and Monte Carlo method

In 1908,Gustow Mie formed a theory in this area in order to understand the mechanism by which suspended colloidal gold particles absorb and scatter different colors of light in water. Mie theory can calculate the exact solution of electromagnetic wave scattering caused by dielectric balls. It can be obtained that the attenuation cross section and scattering cross section of cloud particles are[13]

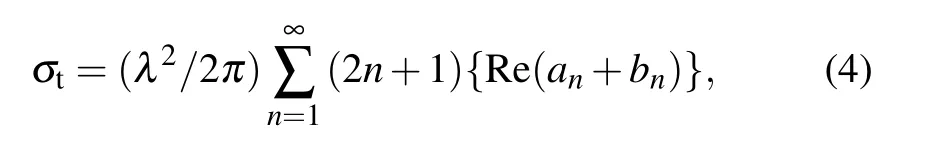
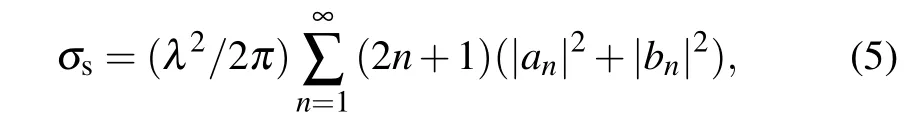
whereλis the wavelength,anandbnare the Mie scattering coefficients. Using parameters such as size parameters and refractive index of the medium,we can obtain the single scattering coefficient and single attenuation cross section of the droplet particles throughsimulation.

The Monte Carlo method treats the problem of radiation transmission by regarding the incident light and the particles in the medium as interacting dispersed particles. There are two situations of scattering and absorption in the transmission of photons in random media. The escape phenomenon occurs at the boundary, and multiple scattering occurs throughout.The process can be described by Markov process. That is,the transfer of the photon sequence is related only to the previous scattering each time.

The weight function is given below:

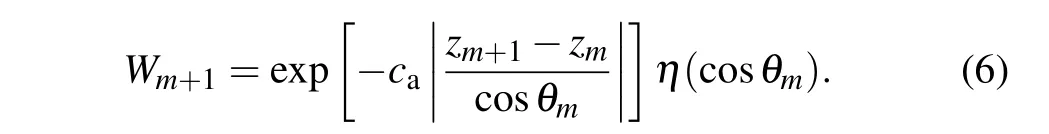
The initial weight of photonW0=1, the angleθiis the angle between thei-th scattering direction of the photon and thez-axis. The estimated function is then as follows:

It is an unbiased estimate of photon transmittance.In the same way,the following equation is obtained:

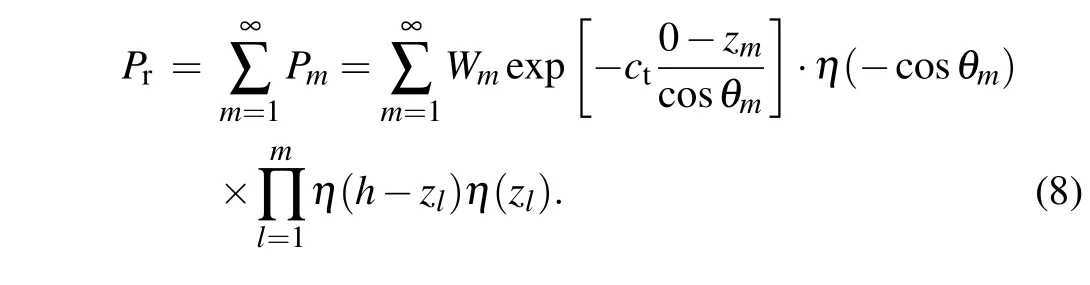
It is an unbiased estimate of reflectivity.In the formula,the exponential part represents the probability with which the photon directly penetrates the cross section from them-th scattering and is not absorbed. The angleθiis the angle between thei-th scattering direction of the photon and thezaxis.[14]LetTbe the average transmittance and expressed as

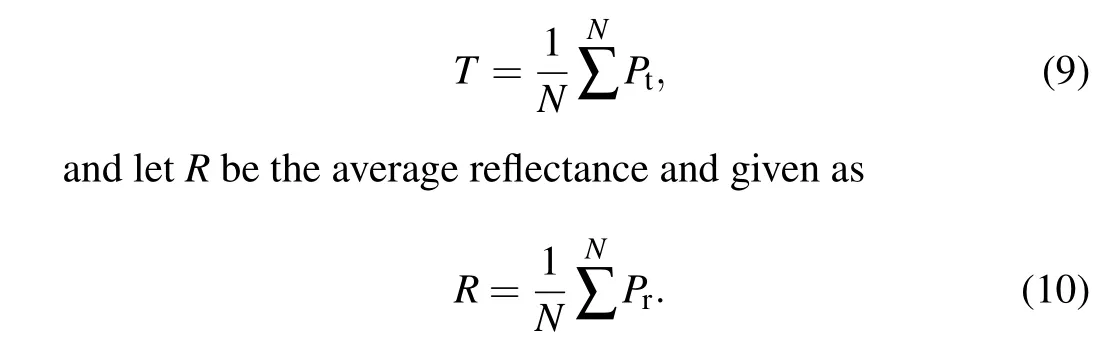
On this basis, in this paper, through the statistical analysis ofPr,the distribution of the number of reflected and transmitted photons in the spatial angle can be obtained.

3.2. Validation of calculation results from Monte Carlo method

According to the medium parameters and the correlation coefficient obtained by Mie theory, the Monte Carlo method can be used to write the program to calculate the scattering and attenuation. This subsection focuses on verifying the scattering results,summarizing the Monte Carlo method,and providing a basis for the subsequent calculation model.

Used in Fig. 2 are the following parameters: medium thicknessd=0.02 cm, particle asymmetry factorg=0.75,albedow0= 0.9, zero-degree incident angle (normal incidence). Figure 2 shows the comparison between the calculation results from Monte Carlo method in this paper and the calculation results in Ref.[15]. On the whole, the fitting results of the two are similar, indicating the accuracy of the calculation results in this paper. In the backscattering,the calculation results in this paper are relatively smoother than the results in the literature. After analysis, it is found that there is an error in the literature with fewer sampling points and fewer photons.Therefore,this paper adopts a unified approach to the photon number: 105to improve the accuracy of calculation.

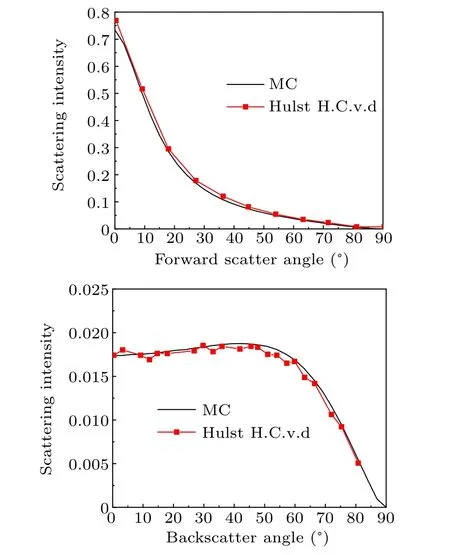
Fig.2. Comparison of scattering data.

The modeling method of laser attenuation and scattering is mainly realized by function fitting. Function fitting is the process of connecting a series of points on a plane by using a smooth curve. In this paper, Origin software is mainly used to fit the attenuation model of laser transmission in fog, and Matlab is used to fit and analyze the backscattering model of laser transmission in fog.

Combining the fitting formula in the literature,[16–20]it is not difficult to see that the model formula for fitting the attenuationAcaused by the laser transmission in the fog can be expressed as a general formula

whereXcan be taken as visibilityVor water contentW,aandbare fitting parameters,corresponding constants are taken according to different wavelengths,and different values ofaandbcan be selected in sections according to different visibility ranges to achieve better fitting results.

In this paper,the Monte Carlo method is also used to calculate the attenuation of the visibility range of 0.01 km–10 km under the incidence of 10.6-µm wavelength laser. The least square method is used to fit the calculation results by using Eq. (11), and two types of fog (advection fog, radiation fog)forward attenuation fitting formulas as follows:

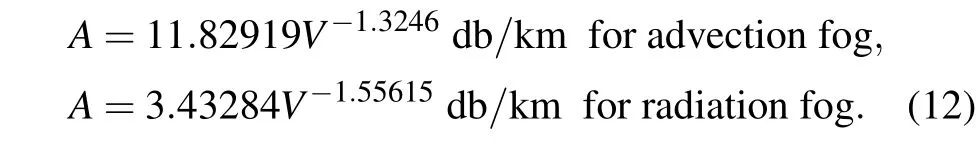
It is not difficult to see that under the incidence of 10.6-µm wavelength laser, various models can be compared. Figure 3 shows the curves drawn from the Kruse attenuation model corrected by Kimet al.,[17]the model proposed by De Boeret al.,[18]the model proposed by Vasseur and Gibbins,[19]and Zhaoet al.,[20]other models,and also the calculations by the Monte Carlo method.

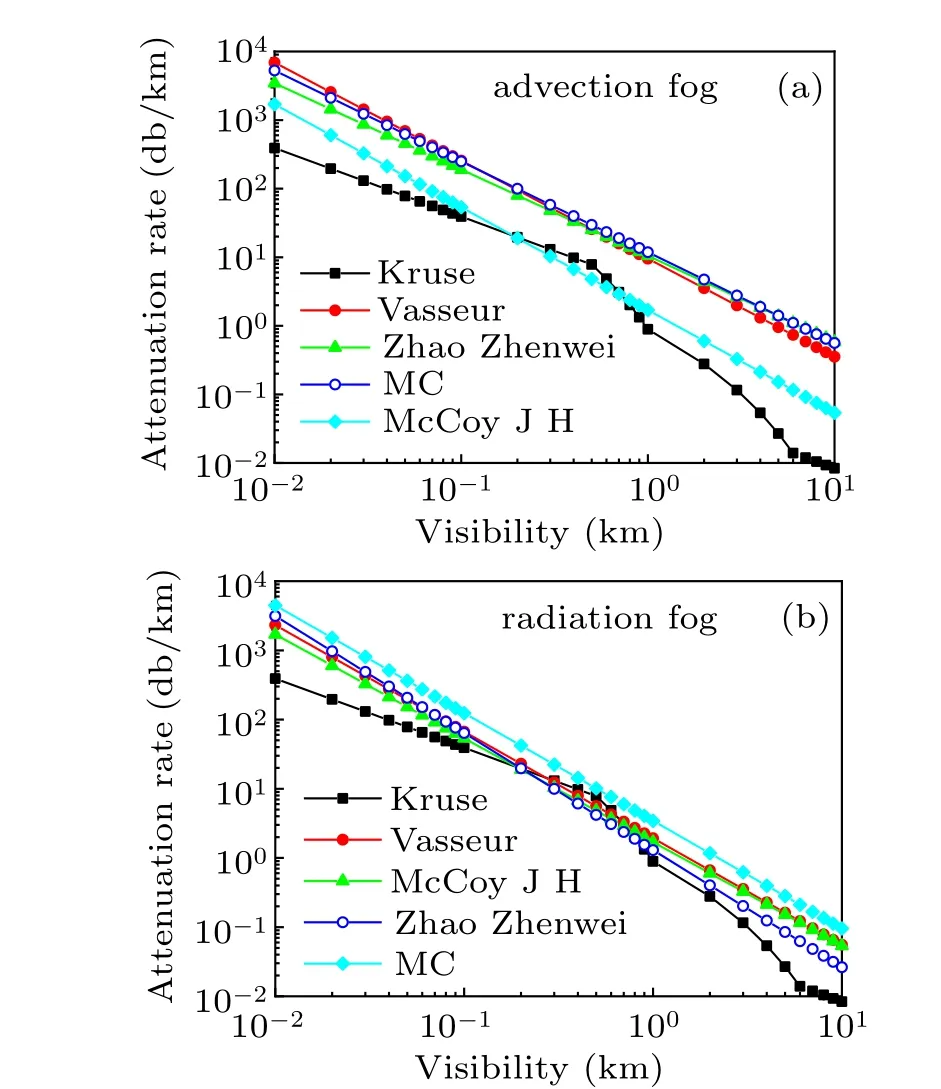
Fig.3. Comparison among various models in(a)advection fog and(b)radiation fog.

As can be seen from Fig. 3, the overall advection fogs in all kinds of fitting curves have slightly larger differences,for all kinds of radiation fogs the calculations are close to fitting curves,which is mainly due to the fact that neither Kruse model nor McCoy J H model distinguishes between advection fog and radiation fog,and by contrasting several curves it can be seen that the calculation results from the models are closer to the calculation results of radiation fog. From Fig. 3(a), in the model proposed by Kruse,McCoy J Het al.,the attenuations are smaller than other results. The results from Vasseur,McCoy J Het al.’s model,and the calculations from the Monte Carlo method in this paper are very close. It can be seen from Fig.3(b)that all kinds of calculation results are relatively close to each other,in which the model proposed by Kruseet al. adopts piecewise fitting. Compared with other curves,the calculation results are lower when the visibility is less than 0.1 km and greater than 1 km. The other models,both experimental and computational, are very close, which shows the accuracy of the monte Carlo method in this paper. At the same time,compared with other models,the Monte Carlo method is much consistent with with the actual situation of low visibility because it takes the multiple scattering into consideration.

4. Model of laser attenuation and scattering in fog

4.1. Attenuation model based on Monte Carlo method

On this basis,in this paper investigated are the transmission attenuation characteristics of laser transmission in advection fog and radiation fog at several other typical wavelengths(0.86 µm, 1.06 µm, 1.315 µm) with visibility in a range of 0.01 km–10 km.

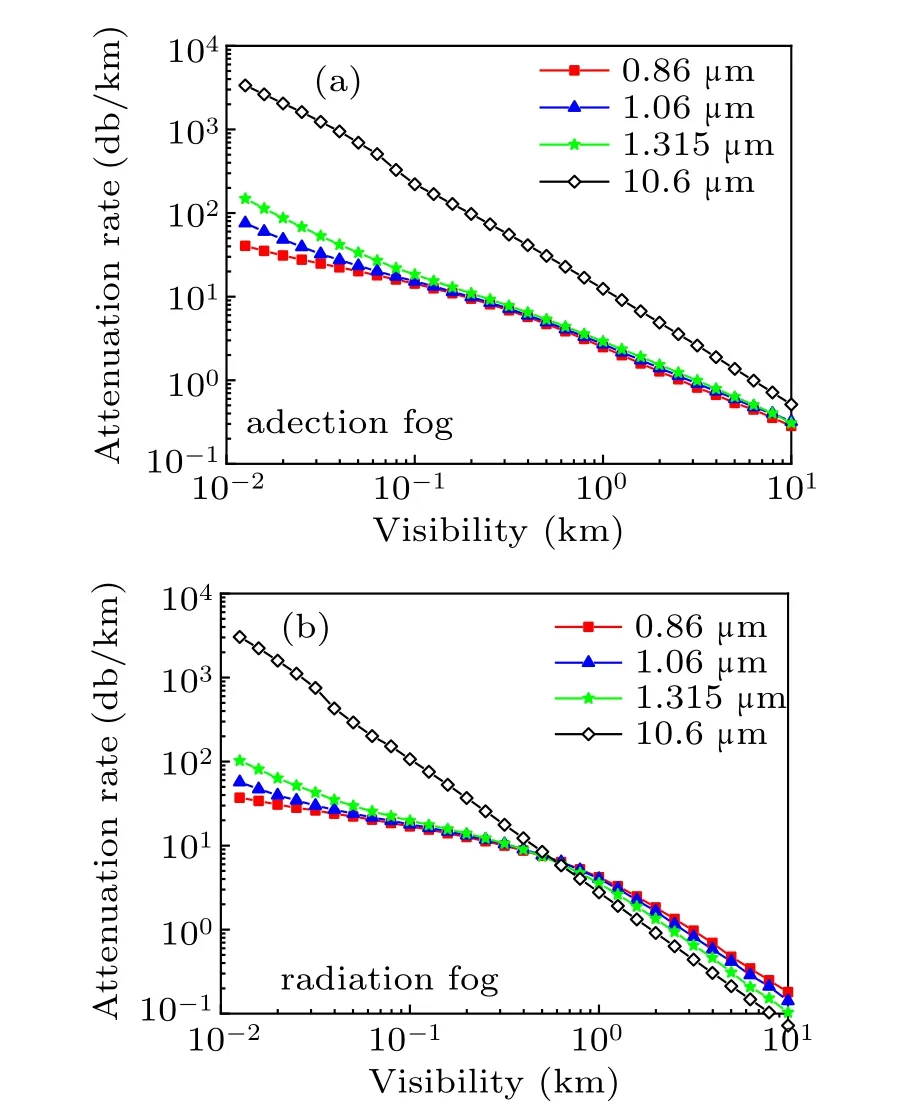
Fig.4. Variation of attenuation rate with visibility in(a)advection fog and(b)radiation fog at different wavelengths.

As can be seen from Fig.4, when the other wavelengths are incident the change of attenuation curve is similar to when the 10.6-µm wavelength laser incidence, especially when the visibility is greater than 1 km, the main difference exists when the visibility is less than 1 km, and the wavelength is longer, and the attenuation is greater. Comparing Fig. 4(a)with Fig.4(b),it can be seen that the attenuation curve of advection fog changes more smoothly than that of radiation fog.

Figure 5 shows the comparison of the single scattering in advection fog and radiation fog at different wavelengths with the multiple scattering results calculated by Monte Carlo method. As can be seen from Figs.5(a)and 5(b), in the case of low visibility, the attenuation rate of single scattering is smaller than that of multiple scattering, and as the visibility increases, the two gradually become similar. As can be seen from Fig.5(b), in the radiation fog, the overall attenuation of single scattering is smaller than that of multiple scattering.This is because in the case of low visibility, the single scattering attenuation underestimates the overall attenuation, we need to use the Monte Carlo method to calculate the attenuation in the case of less visibility.

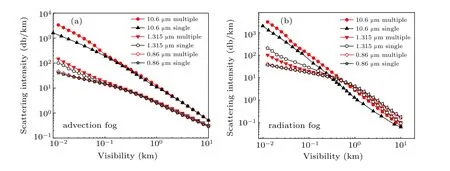
Fig.5. Comparison of single and multiple scattering between(a)advection fog and(b)radiation fog.

For the incidence of laser with 0.86 µm, 1.06 µm, 1.315 µm wavelengths, the slopes of these curves possess constantly changing characteristics. In order to achieve a more accurate fitting function,the curve is divided into three segments(0.01 km–0.1 km,0.1 km–1 km,1 km–10 km)to fit.

Figures 6–8 show the forward attenuation results calculated by Monte Carlo method and the numerical results obtained by Origin piecewise fitting in advection fog and radiation fog at 0.86 µm, 1.06 µm, 1.315 µm, respectively. Equations (13)–(18)represent the attenuation functions of advection fog and radiation fog,respectively. It can be seen from the three figures that the fitting result and the calculation result have a good fit, indicating that the fitting formula basically conforms to the calculation result.

Fig.6. Fitting results of multiple scattering when 0.86-µm wavelength laser is incident in(a)advection fog and(b)radiation fog.

Fig.7. Fitting results of multiple scattering when 1.06-µm wavelength laser is incident in(a)advection fog and(b)radiation fog.

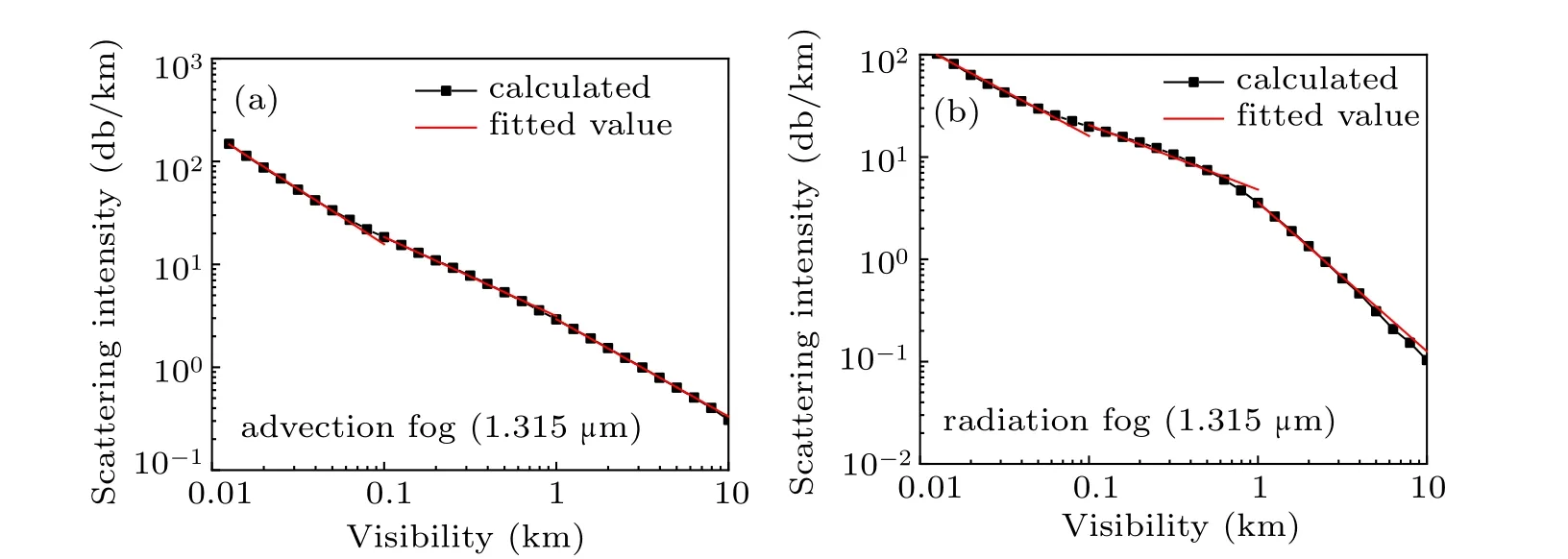
Fig.8. Fitting results of multiple scattering when 1.315-µm wavelength laser is incident in(a)advection fog and(b)radiation fog.

4.2. Backscattering model of laser transmission in fog

For low-visibility environments,backscatter cannot be ignored. Therefore,based on the Monte Carlo method,the data of low-visibility backscatter are calculated. The key point is to calculate the echo characteristics of several typical wavelengths,and then use MATLAB to simulate the data to obtain the engineering model.

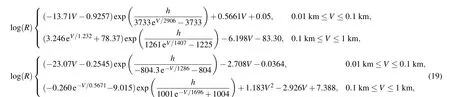
Now, we come to see the incident backward attenuation fitting results of 0.86-µm, 1.06-µm, 1.315-µm, and 10.6-µm wavelength lasers.

The fitting functions of 0.86-µm wavelength laser incident to advection fog and radiation fog attenuations are as follows:

Each group of wavelengths corresponds to four graphs,as shown in Figs.9–12,from left to right and from top to bottom,respectively are ten attenuation curves in advection fog with visibility in a range of 0.01 km–0.1 km;in advection fog,visibility in a range of 0.1 km–1 km has ten attenuation curves;ten attenuation curves with visibility in the range of 0.01 km–0.1 km are in radiation fog;ten attenuation curves with visibility in the range of 0.1 km–1 km are in radiation fog. From top to bottom are the distributions of increasing visibility.

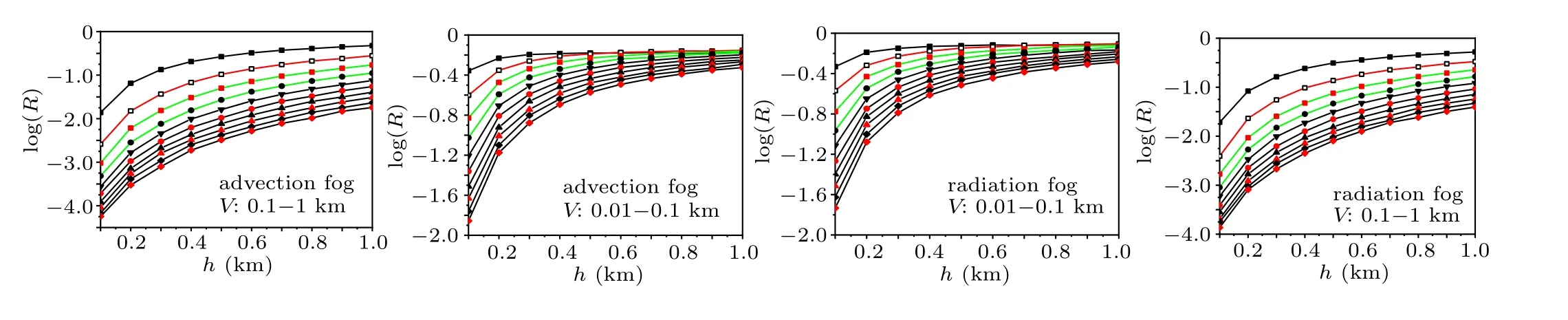
Fig.9. The 0.86-µm wavelength laser incident backward attenuation fitting.

Fig.10. The 1.06-µm wavelength laser incident backward attenuation fitting.

Fig.11. The 1.315-µm wavelength laser incident backward attenuation fitting.

Fig.12. The 10.6-µm wavelength laser incident backward attenuation fitting.

5. Error analysis of laser backscattering model in fog

In the MATLAB fitting process,there are four important fitting parameters in each set of fitting curves: sum of square error(SSE),root mean square(RMSE),coefficient of determination(R-square),sdjusted R-square.

The error values of various fitting data are separately calculated and they are compared with each other as shown in Figs. 13–16.

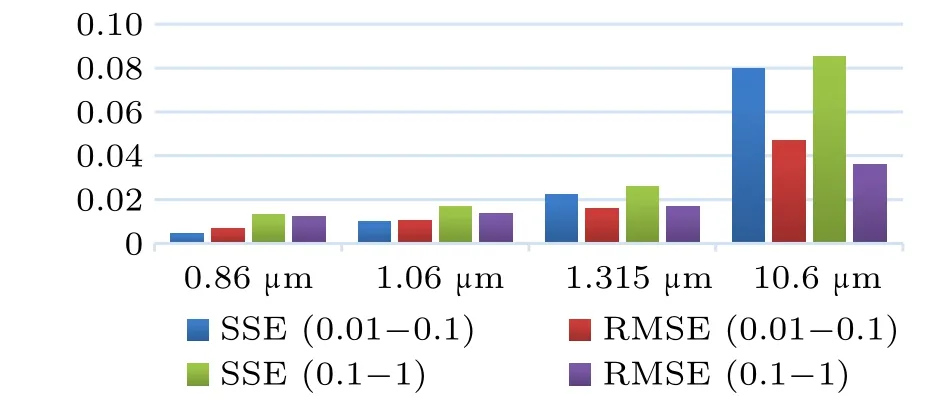
Fig.13. Square sum and root-mean-square statistics of advection fog error.

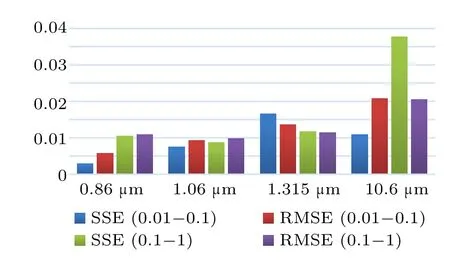
Fig.14. Square sum and root-mean-square statistics of radiation fog error.

The histogram under each wavelength represents in turn from left to right SSE (0.01–0.1), RMSE (0.01–0.1),SSE(0.1–1),and RMSE(0.1–1). It can be seen from Figs.13 and 14 that SSE and RMSE are very close to 0,indicating that the error is very small,the fitting result is close to the calculation result. And comparing the two figures,it can be seen that the fitting in the case of radiant fog is more accurate than in the case of the advection fog. The error of the fitting result when the 10.6-µm wavelength laser is incident is slightly larger,but the error value is still less than 0.1.

The histogram under each wavelength represents in turn from left to right R-square (0.01–0.1), adjusted Rsquare (0.01–0.1), R-square (0.1–1), and adjusted Rsquare (0.1–1). As can be seen from Figs. 15 and 16, the R-square and adjusted R-square are very close to 1 in both the advection fog and the radiation fog,indicating that the fitting results are very close to the overall calculation results,and the fitting error is very small. The fitting error of the 10.6-µm wavelength laser is slightly larger, but the R-square and adjusted R-square are also above 0.9.

Fig.15. Statistics of determination coefficient of advection fog.

Fig.16. Statistics of determination coefficient of radiation fog.

6. Conclusions

In this paper,combining the theory and practice,the laser transmission characteristics in fog are studied, and the engineering model of laser transmission in fog is established. The forward attenuation model of laser transmission in a common fog environment is summarized, and the results of the 10.6-µm wavelength laser calculated by Monte Carlo method in this paper are compared. The results from the model proposed by Vasseur, McCoy J H and others and the Monte Carlo method are investigated in this paper. These results are very close to each other and basically the same, and their change trends are the same, which verifies the correctness of the model in this paper. On this basis, the incident lasers of several typical wavelengths are fitted to the attenuation before and after transmission in fog by using Origin software, and the engineering model is obtained. Considering the effect of low visibility echo characteristics on laser detection, the MATLAB is used to calculate the backward attenuation, an engineering model is obtained. And the fitting error is analyzed in both advection fog and radiation fog. The calculation results, Rsquare and adjusted R-square are very close to 1, indicating that the fitting result is very close to the calculation result as a whole,and the fitting error is very small. The fitting error for the case of the 10.6-µm wavelength laser is slightly larger,but the R-square and adjusted R-square are also above 0.9. The results show that the engineering model fits the calculation results well and has strong application value.