Graphene-tuned threshold gain to achieve optical pulling force on microparticle∗

Hong-Li Chen(陈鸿莉) and Yang Huang(黄杨)

1School of Science,Nantong University,Nantong 226019,China

2School of Science,Jiangsu Provincial Research Center of Light Industrial Optoelectronic Engineering and Technology,Jiangnan University,Wuxi 214122,China

Keywords: pulling force,threshold gain,graphene,microparticle

1. Introduction

The light–matter interaction gives rise to the momentum transfer between light and objects and thus the light usually pushes the object forward. However, one may increase the forward scattering to obtain optical pulling force to pull the object towards the light source.[1–6]The optical pulling force could be achieved via Gaussian beam,[7,8]Bessel beam,[9]and other tractor beams. Moreover, optical pulling forces acting on chiral,[10–12]hyperbolic[13]or gain[14–16]materials have been investigated. The pulling force would be achieved only when the appropriate gain is introduced in the structure.[15]The threshold gain for pulling force was obtained analytically for Rayleigh spheres,thin cylinders,and thin slabs.[16]In addition, the continuous modulation from pushing to pulling force was exhibited by controlling the incident angle of the interfering plane waves near Fano resonance of the plasmonic nanoparticle.[17]The optical force could be enhanced at the plasmonic resonance and these results have been applied to quantum measurement, signal detection, and other fields.[18–22]Furthermore,the tunable optical pulling forces on plasmonic nanostructures have been demonstrated at plasmon singularity and Fano resonance, and the giant pulling force was achieved due to the reversal of the electric field.[23,24]Fano resonance originating from the interference of simultaneously excited multipoles could also produce the pulling force on plasmonic nanoparticles.[25]Therefore,the optical pulling force could be achieved due to the resonance of the plasmonic structure.

Graphene, as a new kind of plasmonic material, has unique optical and electronic properties such as excellent electro-optic tunability,[26,27]optical nonlinearity,[28,29]plasmonic dissipation,[30]and extremely high electromagnetic field concentration.[31]As a consequence, it has potential applications in modulators,[32,33]optical sensing, polarizers,mid-infrared photodetectors,and many others.[34,35]The plasmonic property of the graphene layer is comparable to that of thin metal sheets with a thickness of tens of nanometers.[36]In comparison with surface plasmon on a metal–dielectric interface,the graphene plasmon is superior due to the strong confinement of electromagnetic energy.[37]The high-sensitivity tunable plasmonic biosensor had been demonstrated and the spatial light confinement in graphene was two orders of magnitude higher than that in metal.[38]The multi-band perfect plasmonic absorptions have been achieved in singlelayer graphene-based rectangular gratings via the excitation of standing-wave graphene surface plasmon polaritons.[39]

In our previous study, we have investigated the bistability of the optical force on nonlinear graphene-wrapped nanoparticles.[40]Here,we aim to explore the graphene-tuned threshold gain to obtain optical pulling force on the gain microparticle. We demonstrate that the coupling of the dipole mode with quadrupole mode produces a Fano-profile optical force at resonance wavelength when the imaginary part of the permittivity for the gain value reaches a threshold gain. At the same time, the reversal of the pulling force and the pushing force appear. In addition,the pulling force or the pushing force can be enhanced if the gain value is close to the threshold gain at plasmonic resonance. The graphene-tuned optical force is also analyzed by adjusting the Fermi energy and relaxation time of the graphene. The threshold gain is strongly dependent on the relaxation time, but independent of Fermi energy value. Moreover, the pulling force on large microparticle is easy to obtain near octupole resonance with small gain value. And to achieve the pulling force near quadrupole resonance, the threshold gain should be further increased. Our results take advantage of the technology of graphene plasmon and provide an alternative way to manipulate gain particles.

2. Model and theories

wheree,EF,,τare electron charge, Fermi energy, reduced Planck constant,and electron–photon relaxation time,respectively. Note that equation(1)is valid when the interband transition is negligible compared with intraband one under the condition ofEF＞ωat room temperature.

Fig. 1. Schematic diagram of graphene-coated gain microparticle illuminated by plane wave propagating along z axis.

The time-averaged optical force〈F〉on the graphenecoated gain microparticle is expressed as an integration of Maxwell’s stress tensorover surfaceSsurrounding the microparticle[23,25]

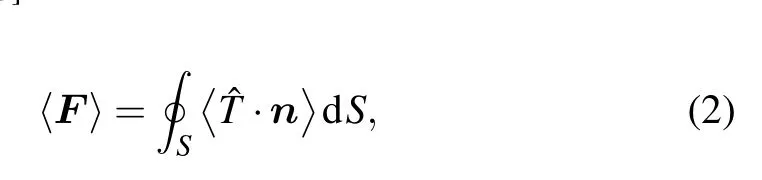
wherenis the unit normal vector pointing outwards to the surfaceS, andrelates to the electromagnetic fields which can be obtained by Mie theory.[47]And the scattering efficiency for the graphene-coated gain microparticle is defined as

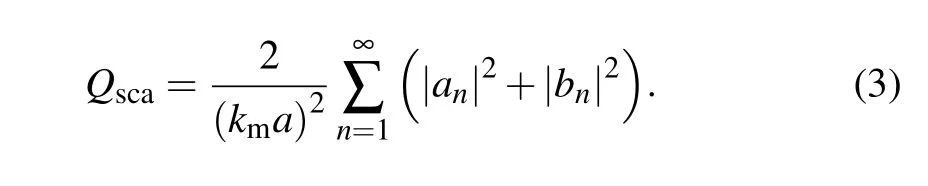
Here,anandbnare Mie coefficients associated with the electric and magnetic multipolar modes, respectively, and expressed as[48]

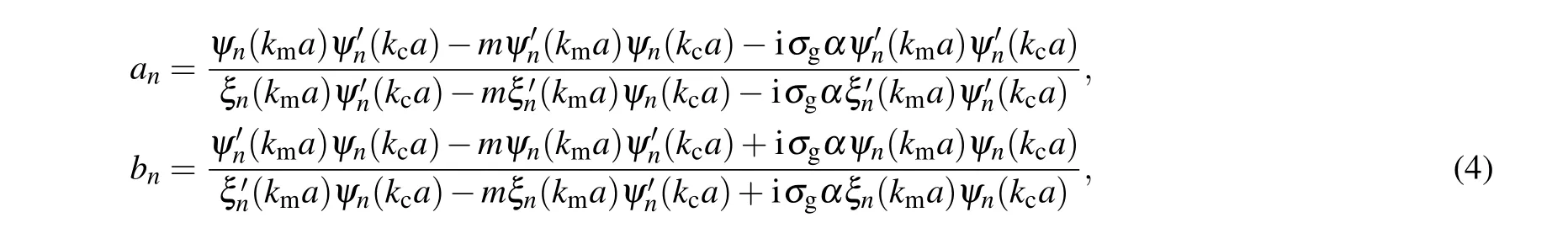
3. Numerical results and discussion

Now we come to calculate the optical force on the graphene-coated gain microparticle witha=5 µm andεcr=1.5(the glass composite with some air holes). For simplicity,the background medium is assumed to be vacuum withεm=1.

As shown in Fig. 2(a), two resonant peaks of pushing force are found to be atλ=45.1µm andλ=62.4µm forεci=0.040. Interestingly, the Fano-profile optical force accompanied by pulling force arises with the gain value increasing uponεci=0.085 atλ=45.1µm. Further increasing the gain toεci= 0.120, the Fano-profile force switches to the pulling force peak.To investigate the resonant peaks of optical force, the scattering efficiency of the microparticle is studied in Fig. 2(b). It is shown that the total scattering efficiency is contributed mainly from the dipole mode (n=1) with the incident wavelength ranging from 50µm to 80µm. The narrow quadrupole mode (n=2) appears as the wavelength decreases,and we can predict that the Fano-profile optical force results from the coupling of broad dipolar mode with narrow quadrupole mode. For the further study of these resonances,we plot the electric fields in Fig.3,demonstrating that the resonance is induced by the plasmonic resonance of the graphene shell due to the metallicity of graphene. The dipole resonance is presented atλ=62.4µm and quadrupole resonance occurs atλ=45.1µm.

Fig. 2. (a) Optical force F on graphene-coated gain microparticle and (b)scattering efficiency Qsca versus incident wavelength λ for εci=0.085.With other parameters being a=5µm, εcr =1.5, EF =0.7 eV, τ =1 ps, and εm=1.

Fig.3. Electric fields for graphene-coated gain microparticle at wavelength λ =62.4µm(a)and 45.1µm(b).

For the in-depth discussion of optical force near quadruple resonance, figure 4(a) shows the optical forceFatλ=45.1µm with respect to the gain valueεci. It indicates that the optical pushing force appears for small gain values, and becomes pulling force when the gain value arrives atεci=0.085,which is called threshold gain. Figure 4(a)clearly shows that the reversal of optical pushing and pulling force, and also reveals the pushing or pulling force dramatically decreases if the gain value is far from the threshold gain. Therefore, the threshold gain is important not only for obtaining the optical pulling force but also for enhancing the optical force. Moreover, the scattering intensityS(θ) for the microparticle with threshold gainεci=0.085 is discussed as shown in Fig.4(b).The forward scattering is much stronger than the backward one atλ=45.1µm,therefore the optical pulling force arises due to the conversation of momentum.

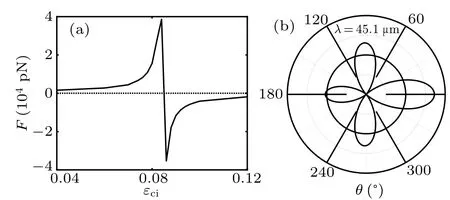
Fig. 4. (a) Optical force F versus gain value εci, and (b) scattering intensity S(θ)for the graphene-coated gain microparticle,with other parameters being λ=45.1µm,a=5µm,εcr=1.5,EF=0.7 eV,τ=1 ps,and εm=1.

Fig.5. Optical force F versus incident wavelength λ for(a)different values of EF with τ=1 ps and(b)different values of τ with EF=0.7 eV,with insert showing the threshold gain and other parameters being a=5µm,εcr=1.5,εci=0.085,and εm=1.

Now, we study the influence of Fermi energyEFand relaxation timeτon the optical forceF. Figure 5(a)shows that the peak of optical force is blue-shifted and the pulling force near quadrupole resonance slightly increases with Fermi energyEFincreasing. In addition, the Fano-profile is still well maintained for different values of Fermi energy, which indicates that the threshold gain is almost unchanged for pulling force with different values of Fermi energy. And the threshold gainversusFermi energy is plotted in the inset of Fig. 5(a).On the contrary, in Fig. 5(b), when increasing the relaxation timeτ, the optical force peak does not shift, but the pushing force at dipole resonance is strongly enhanced on the account of lower energy dissipation with larger relaxation time.[46]Meanwhile,the optical force can reverse from pulling/pushing to pushing/pulling force with the tunable relaxation time at quadrupole resonance,which is different from the scenario in Fig. 5(a). For further study, the threshold gainversusthe relaxation time is plotted in the inset of Fig.5(b). It shows that the threshold gain decreases with relaxation time increasing,which explain the transformation in the direction of optical force at quadrupole resonance by tuning the relaxation timeτ. In other words,the threshold gainεci=0.085 forτ=1 ps is not sufficient to trap the graphene-coated gain microparticle forτ=0.5 ps,but it will be enough to generate large pulling force forτ=1.5 ps,which is shown in Fig.5(b).

In the end, we consider the optical forceFon the larger graphene-coated gain microparticle witha=10µm together with the scattering efficiencyQscaand scattering intensityS(θ)in Fig.6. It is worth mentioning that the octupole mode plays a role in the total force for larger microparticle. Figure 6(a) shows that there is Fano-profile optical force at the octupole resonance when the imaginary part of the permittivity arrives at gain valueεci=0.083. Figure 6(b) reveals that the Fano resonance arises from the coupling of quadrupole mode(n=2)with octupole one(n=3). If the gain value increases toεci=0.163, the Fano-profile pulling force appears at quadrupole resonance. It is shown that the threshold gain for optical pulling force induced by the interference of dipole mode with quadrupole mode will increase for larger graphenecoated gain microparticle. Meanwhile,it is easy to achieve the pulling force at octupole resonance with small gain in the large particle case.Figure 6(c)presents the scattering intensityS(θ)for the large microparticle withεci=0.083. As expected,the forward scattering is much larger than the backward one at octupole resonanceλ=54.2µm,which gives rise to the optical pulling force.

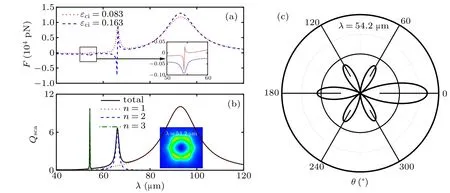
Fig.6.(a)Optical force F on larger graphene-coated gain microparticle and(b)scattering efficiency Qsca versus incident wavelength λ,and(c)scattering intensity S(θ)for the coated microparticle with εci=0.083,with other parameters being a=10µm,εcr=1.5,EF=0.7 eV,τ =1 ps,and εm=1.

4. Conclusions

In this work,we studied the optical force on the graphenecoated gain microparticle by the Maxwell’s stress tensor method and Mie theory. The coupling of dipole mode with quadrupole mode produces a Fano-profile optical force along with pulling force if the gain value arrives at a threshold gain.And the optical force will be dramatically enhanced near the threshold gain. The threshold gain is sensitive to the relaxation time,irrespective of Fermi energy value. As to the case of larger particles,the optical pulling force appears at octupole resonance with small gain and the threshold gain increases to get an optical pulling force at quadrupole resonance. These results provide an in-depth insight into the mechanism of the optical pulling force on gain particles,as well as offer potential applications in optical manipulating microparticles.